2020年苏科新版八年级上册数学《第1章 全等三角形》单元测试卷(解析版)
文档属性
| 名称 | 2020年苏科新版八年级上册数学《第1章 全等三角形》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 323.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 15:52:14 | ||
图片预览


文档简介
2020年苏科新版八年级上册数学《第1章 全等三角形》单元测试卷
一.选择题(共10小题)
1.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.三角形 D.平行四边形
2.下列图形中有稳定性的是( )
A.正方形 B.直角三角形 C.长方形 D.平行四边形
3.下列叙述中错误的是( )
A.能够完全重合的图形称为全等图形
B.全等图形的形状和大小都相同
C.所有正方形都是全等图形
D.形状和大小都相同的两个图形是全等图形
4.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
A.90° B.135° C.150° D.180°
5.如图,两个三角形为全等三角形,则∠α的度数是( )
A.72° B.60° C.58° D.50°
6.如图,△ABO≌△DCO,∠D=80°,∠DOC=70°,则∠B=( )
A.35° B.30° C.25° D.20°
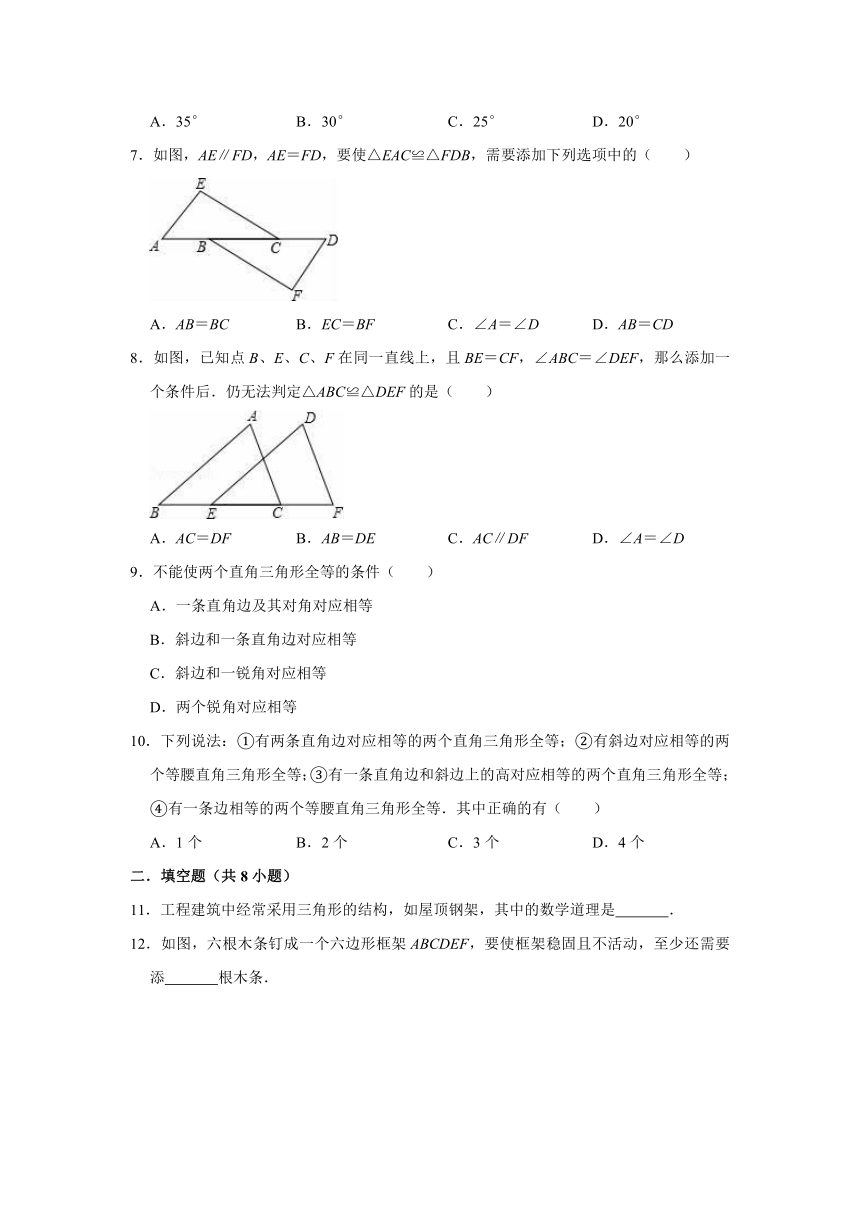
7.如图,AE∥FD,AE=FD,要使△EAC≌△FDB,需要添加下列选项中的( )
A.AB=BC B.EC=BF C.∠A=∠D D.AB=CD
8.如图,已知点B、E、C、F在同一直线上,且BE=CF,∠ABC=∠DEF,那么添加一个条件后.仍无法判定△ABC≌△DEF的是( )
A.AC=DF B.AB=DE C.AC∥DF D.∠A=∠D
9.不能使两个直角三角形全等的条件( )
A.一条直角边及其对角对应相等
B.斜边和一条直角边对应相等
C.斜边和一锐角对应相等
D.两个锐角对应相等
10.下列说法:①有两条直角边对应相等的两个直角三角形全等;②有斜边对应相等的两个等腰直角三角形全等;③有一条直角边和斜边上的高对应相等的两个直角三角形全等;④有一条边相等的两个等腰直角三角形全等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题)
11.工程建筑中经常采用三角形的结构,如屋顶钢架,其中的数学道理是 .
12.如图,六根木条钉成一个六边形框架ABCDEF,要使框架稳固且不活动,至少还需要添 根木条.
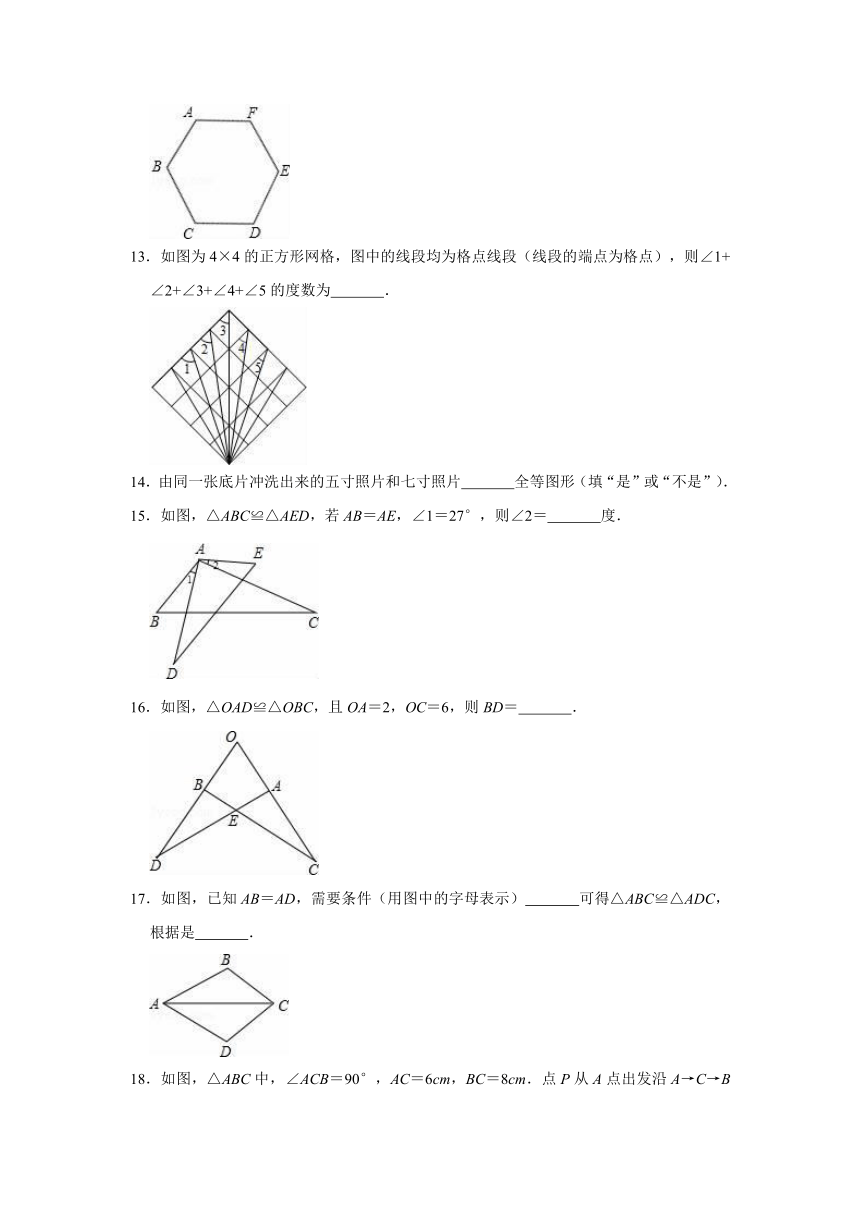
13.如图为4×4的正方形网格,图中的线段均为格点线段(线段的端点为格点),则∠1+∠2+∠3+∠4+∠5的度数为 .
14.由同一张底片冲洗出来的五寸照片和七寸照片 全等图形(填“是”或“不是”).
15.如图,△ABC≌△AED,若AB=AE,∠1=27°,则∠2= 度.
16.如图,△OAD≌△OBC,且OA=2,OC=6,则BD= .
17.如图,已知AB=AD,需要条件(用图中的字母表示) 可得△ABC≌△ADC,根据是 .
18.如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t= 秒时,△PEC与△QFC全等.
三.解答题(共8小题)
19.如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上,∠A=50°,∠F=40°.
(1)求△DBE各内角的度数;
(2)若AD=16,BC=10,求AB的长.
20.如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,求∠A的度数.
21.已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.
求证:△ABC≌△DEF.
22.如图,∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?
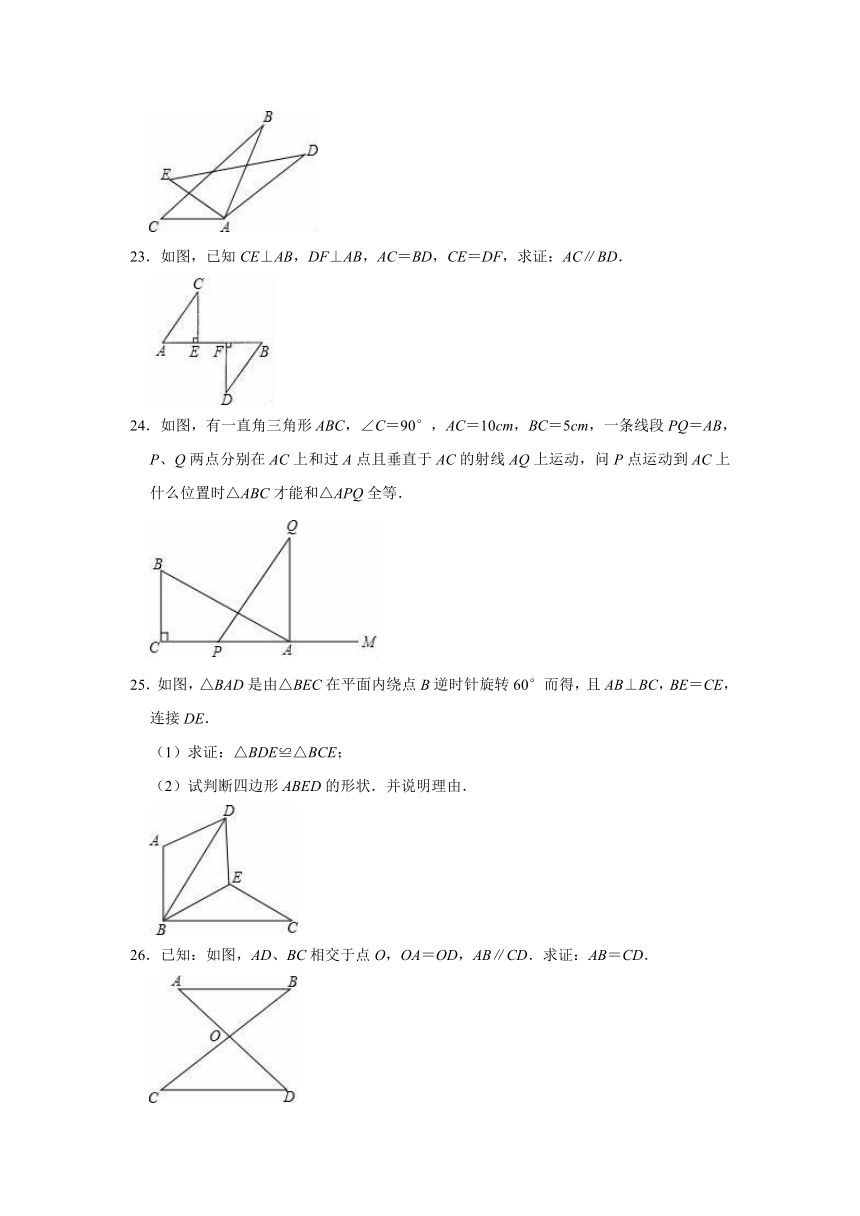
23.如图,已知CE⊥AB,DF⊥AB,AC=BD,CE=DF,求证:AC∥BD.
24.如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
25.如图,△BAD是由△BEC在平面内绕点B逆时针旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状.并说明理由.
26.已知:如图,AD、BC相交于点O,OA=OD,AB∥CD.求证:AB=CD.
2020年苏科新版八年级上册数学《第1章 全等三角形》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.三角形 D.平行四边形
【分析】根据三角形具有稳定性解答.
【解答】解:根据三角形具有稳定性,可得四个选项中只有直角三角形具有稳定性.
故选:C.
【点评】本题考查了三角形具有稳定性,是基础题,需熟记.
2.下列图形中有稳定性的是( )
A.正方形 B.直角三角形 C.长方形 D.平行四边形
【分析】根据三角形具有稳定性可得答案.
【解答】解:直角三角形有稳定性,
故选:B.
【点评】此题主要考查了三角形的稳定性,是需要识记的内容.
3.下列叙述中错误的是( )
A.能够完全重合的图形称为全等图形
B.全等图形的形状和大小都相同
C.所有正方形都是全等图形
D.形状和大小都相同的两个图形是全等图形
【分析】能够完全重合的两个图形叫做全等形,结合各选项进行判断即可.
【解答】解:A、能够重合的图形称为全等图形,说法正确,故本选项错误;
B、全等图形的形状和大小都相同,说法正确,故本选项错误;
C、所有正方形不一定都是全等图形,说法错误,故本选项正确;
D、形状和大小都相同的两个图形是全等图形,说法正确,故本选项错误;
故选:C.
【点评】本题考查了全等图形的知识,要求同学们掌握全等图形的定义及性质.
4.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
A.90° B.135° C.150° D.180°
【分析】标注字母,利用“边角边”判断出△ABC和△DEA全等,根据全等三角形对应角相等可得∠1=∠4,然后求出∠1+∠3=90°,再判断出∠2=45°,然后计算即可得解.
【解答】解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠1=∠4,
∵∠3+∠4=90°,
∴∠1+∠3=90°,
又∵∠2=45°,
∴∠1+∠2+∠3=90°+45°=135°.
故选:B.
【点评】本题考查了全等图形,网格结构,准确识图判断出全等的三角形是解题的关键.
5.如图,两个三角形为全等三角形,则∠α的度数是( )
A.72° B.60° C.58° D.50°
【分析】根据三角形内角和定理计算出∠1的度数,然后再根据全等三角形的对应角相等可得∠α=∠1=72°.
【解答】解:根据三角形内角和可得∠1=180°﹣50°﹣58°=72°,
因为两个全等三角形,
所以∠α=∠1=72°,
故选:A.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应角相等.
6.如图,△ABO≌△DCO,∠D=80°,∠DOC=70°,则∠B=( )
A.35° B.30° C.25° D.20°
【分析】根据三角形内角和定理求出∠C,根据全等三角形的性质解答即可.
【解答】解:∵∠D=80°,∠DOC=70°,
∴∠C=180°﹣∠D﹣∠DOC=30°,
∵△ABO≌△DCO,
∴∠B=∠C=30°,
故选:B.
【点评】本题考查的是全等三角形的性质、三角形内角和定理,掌握全等三角形的对应角相等是解题的关键.
7.如图,AE∥FD,AE=FD,要使△EAC≌△FDB,需要添加下列选项中的( )
A.AB=BC B.EC=BF C.∠A=∠D D.AB=CD
【分析】添加条件AB=CD可证明AC=BD,然后再根据AE∥FD,可得∠A=∠D,再利用SAS定理证明△EAC≌△FDB即可.
【解答】解:∵AE∥FD,
∴∠A=∠D,
∵AB=CD,
∴AC=BD,
在△AEC和△DFB中,
∴△EAC≌△FDB(SAS),
故选:D.
【点评】此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
8.如图,已知点B、E、C、F在同一直线上,且BE=CF,∠ABC=∠DEF,那么添加一个条件后.仍无法判定△ABC≌△DEF的是( )
A.AC=DF B.AB=DE C.AC∥DF D.∠A=∠D
【分析】根据全等三角形的判定方法逐项判断即可.
【解答】解:
∵BE=CF,
∴BE+EC=EC+CF,即BC=EF,且∠ABC=∠DEF,
∴当AC=DF时,满足SSA,无法判定△ABC≌△DEF,故A不能;
当AB=DE时,满足SAS,可以判定△ABC≌△DEF,故B可以;
当AC∥DF时,可得∠ACB=∠F,满足ASA,可以判定△ABC≌△DEF,故C可以;
当∠A=∠D时,满足AAS,可以判定△ABC≌△DEF,故D可以;
故选:A.
【点评】本题主要考查全等三角形的判定方法,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.
9.不能使两个直角三角形全等的条件( )
A.一条直角边及其对角对应相等
B.斜边和一条直角边对应相等
C.斜边和一锐角对应相等
D.两个锐角对应相等
【分析】根据各选项提供的已知条件,结合直角三角形全等的判定方法,对选项逐一验证,选项D只有两个锐角对应相等是不符合直角三角形判定方法的,所以不能判定三角形全等.
【解答】解:A、符合AAS,正确;
B、符合HL,正确;
C、符合ASA,正确;
D、因为判定三角形全等必须有边的参与,错误.
故选:D.
【点评】此题主要考查全等三角形的判定方法的掌握情况.判断全等时必须要有边对应相等的关系.
10.下列说法:①有两条直角边对应相等的两个直角三角形全等;②有斜边对应相等的两个等腰直角三角形全等;③有一条直角边和斜边上的高对应相等的两个直角三角形全等;④有一条边相等的两个等腰直角三角形全等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据判定两直角三角形全等的判定方法进行判断即可.
【解答】解:①有两条直角边对应相等的两个直角三角形全等,可利用SAS判定两直角三角形全等;
②有斜边对应相等的两个等腰直角三角形全等,可利用ASA判定两直角三角形全等;
③有一条直角边和斜边上的高对应相等的两个直角三角形全等,能判定两直角三角形全等;
④有一条边相等的两个等腰直角三角形全等,不能判定两直角三角形全等.
故选:C.
【点评】本题考查了直角三角形全等的判定方法,直角三角形首先是三角形,所以一般三角形全等的判定方法都适合它,同时,直角三角形又是特殊的三角形,有它的特殊性,作为“HL”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
二.填空题(共8小题)
11.工程建筑中经常采用三角形的结构,如屋顶钢架,其中的数学道理是 三角形具有稳定性 .
【分析】根据三角形具有稳定性解答即可.
【解答】解:工程建筑中经常采用三角形的结构,如屋顶钢架,其中的数学道理是三角形具有稳定性,
故答案为:三角形具有稳定性.
【点评】此题主要考查了三角形的稳定性,是需要记忆的内容.
12.如图,六根木条钉成一个六边形框架ABCDEF,要使框架稳固且不活动,至少还需要添 3 根木条.
【分析】根据三角形的稳定性,只要使六边形框架ABCDEF变成三角形的组合体即可.
【解答】解:根据三角形的稳定性,得
如图:从图中可以看出,要使框架稳固且不活动,至少还需要添3根木条.
【点评】本题主要考查的是三角形的稳定性.
13.如图为4×4的正方形网格,图中的线段均为格点线段(线段的端点为格点),则∠1+∠2+∠3+∠4+∠5的度数为 225° .
【分析】根据正方形的性质可得出∠3=45°,根据长方形的性质即可得出相等的边,由此可得出全等的三角形,进而得出∠1与∠5互余、∠2与∠4互余,再将其代入∠1+∠2+∠3+∠4+∠5中即可得出结论.
【解答】解:在图中标上字母,如图所示.
∵四边形ABCD为4×4的正方形,
∴∠3=45°.
∵四边形ANPE为1×1的正方形,
∴AE=AN.
∵四边形CDEF和四边形BCMN均为4×3的长方形,
∴CE=CN.
在△ACE和△ACN中,,
∴△ACE≌△ACN(SSS),
∴∠AEC=∠ANC,
∴∠2+∠4+90°=180°,
∴∠2与∠4互余.
同理可得:∠1与∠5互余.
∴∠1+∠2+∠3+∠4+∠5=(∠1+∠5)+(∠2+∠4)+∠3=90°+90°+45°=225°.
故答案为:225°.
【点评】本题考查了全等图形、全等三角形的判定与性质、长方形及正方形的性质,解题的关键是找出∠3=45°、∠1与∠5互余、∠2与∠4互余.
14.由同一张底片冲洗出来的五寸照片和七寸照片 不是 全等图形(填“是”或“不是”).
【分析】能够完全重合的两个图形叫做全等形,图形重合的是全等形,不重合的不是全等形.
【解答】解:由全等形的概念可知:由同一张底片冲洗出来的五寸照片和七寸照片,大小不一样,所以不是全等图形.
故答案为:不是.
【点评】本题考查了全等形的概念,判定是不是全等形主要看图形是不是能够重合.
15.如图,△ABC≌△AED,若AB=AE,∠1=27°,则∠2= 27 度.
【分析】先运用三角形全等求出∠BAC=∠EAD,则∠2易求.
【解答】解:∵△ABC≌△AED,AB=AE,
∴∠BAC=∠EAD
∴∠2=∠1=27°.
【点评】本题考查了全等三角形的性质;全等三角形的对应边相等,对应角相等,是需要识记的内容,找准对应角是解题的关键.
16.如图,△OAD≌△OBC,且OA=2,OC=6,则BD= 4 .
【分析】根据全等三角形的性质可得DO=CO=6,BO=AO=2,再利用线段的和差关系可得答案.
【解答】解:∵△OAD≌△OBC,
∴DO=CO=6,BO=AO=2,
∴BD=6﹣2=4,
故答案为:4.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等.
17.如图,已知AB=AD,需要条件(用图中的字母表示) BC=DC 可得△ABC≌△ADC,根据是 SSS .
【分析】添加条件BC=DC,可直接利用SSS定理判定△ABC≌△ADC.
【解答】解:添加条件BC=DC,
∵在△ABC和△ADC中,
∴△ABC≌△ADC(SSS),
故答案为:BC=DC;SSS.
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
18.如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t= 1或或12 秒时,△PEC与△QFC全等.
【分析】根据题意化成三种情况,根据全等三角形的性质得出CP=CQ,代入得出关于t的方程,求出即可.
【解答】解:分为三种情况:①如图1,P在AC上,Q在BC上,
∵PE⊥l,QF⊥l,
∴∠PEC=∠QFC=90°,
∵∠ACB=90°,
∴∠EPC+∠PCE=90°,∠PCE+∠QCF=90°,
∴∠EPC=∠QCF,
则△PCE≌△CQF,
∴PC=CQ,
即6﹣t=8﹣3t,
t=1;
②如图2,P在BC上,Q在AC上,
∵由①知:PC=CQ,
∴t﹣6=3t﹣8,
t=1;
t﹣6<0,即此种情况不符合题意;
③当P、Q都在AC上时,如图3,
CP=6﹣t=3t﹣8,
t=;
④当Q到A点停止,P在BC上时,AC=PC,t﹣6=6时,解得t=12.
P和Q都在BC上的情况不存在,∵P的速度是每秒1cm,Q的速度是每秒3cm;
故答案为:1或或12.
【点评】本题考查了全等三角形的判定和性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等.
三.解答题(共8小题)
19.如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上,∠A=50°,∠F=40°.
(1)求△DBE各内角的度数;
(2)若AD=16,BC=10,求AB的长.
【分析】(1)根据全等三角形的性质求出∠D、∠E,根据三角形内角和定理求出∠EBD即可;
(2)根据全等三角形的性质得出AC=BD,求出AB=CD,即可求出答案.
【解答】解:(1)∵△ACF≌△DBE,∠A=50°,∠F=40°,
∴∠D=∠A=50°,∠E=∠F=40°,
∴∠EBD=180°﹣∠D﹣∠E=90°;
(2)∵△ACF≌△DBE,
∴AC=BD,
∴AC﹣BC=DB﹣BC,
∴AB=CD,
∵AD=16,BC=10,
∴AB=CD=(AD﹣BC)=3.
【点评】本题考查了全等三角形的性质的应用,能熟记全等三角形的性质是解此题的关键,注意:全等三角形的对应角相等,对应边相等.
20.如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,求∠A的度数.
【分析】根据全等三角形对应边相等可得OB=OD,全等三角形对应角相等可得∠ABO=∠D,再根据等边对等角求出∠OBD=∠D,然后求出∠ABC,再根据两直线平行,内错角相等解答即可.
【解答】解:∵△ABO≌△CDO,
∴OB=OD,∠ABO=∠D,
∴∠OBD=∠D=(180°﹣∠BOD)=×(180°﹣30)=75°,
∴∠ABC=180°﹣75°×2=30°,
∴∠A=∠ABC=30°.
【点评】本题考查了全等三角形的性质,等边对等角的性质,平行线的性质,熟记性质并准确识图是解题的关键.
21.已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.
求证:△ABC≌△DEF.
【分析】直接利用全等三角形的判定方法得出答案.
【解答】证明:∵AB∥DE,
∴∠B=∠DEF
∵BE=FC,
∴BC=EF,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
【点评】此题主要考查了全等三角形的判定,全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.
22.如图,∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?
【分析】根据∠CAE=∠BAD,可得∠CAB=∠EAD,又已知∠B=∠D,AC=AE,可利用AAS证明△ABC≌△ADE.
【解答】解:△ABC≌△ADE.
∵∠CAE=∠BAD,
∴∠CAB=∠EAD,
在△ABC和△ADE,
∵,
∴△ABC≌△ADE(AAS).
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
23.如图,已知CE⊥AB,DF⊥AB,AC=BD,CE=DF,求证:AC∥BD.
【分析】利用已知条件可直接证出Rt△ACE≌Rt△BDF(HL),可得到对应角∠A=∠B,根据内错角相等,两直线平行可证得AC∥BD.
【解答】证明:∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°.
又∵AC=BD,CE=DF,
∴Rt△ACE≌Rt△BDF(HL).
∴∠A=∠B,
∴AC∥BD.
【点评】本题考查了全等三角形的判定和性质以及平行线的判定定理等知识.
24.如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
【分析】本题要分情况讨论:①Rt△APQ≌Rt△CBA,此时AP=BC=5cm,可据此求出P点的位置.
②Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合.
【解答】解:根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=5cm;
②当P运动到与C点重合时,AP=AC,
在Rt△ABC与Rt△QPA中,
,
∴Rt△QAP≌Rt△BCA(HL),
即AP=AC=10cm,
∴当点P与点C重合时,△ABC才能和△APQ全等.
综上所述,当P运动到AP=BC、点P与点C重合时,△ABC才能和△APQ全等.
【点评】本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.
25.如图,△BAD是由△BEC在平面内绕点B逆时针旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状.并说明理由.
【分析】(1)根据SAS即可证明△BDE≌△BCE.
(2)根据四边相等的四边形是菱形即可判定.
【解答】解:(1)证明:∵由旋转可知,AB=EB,AD=EC,BD=BC,∠ABD=∠EBC,∠ABE=∠DBC=60°,
∵AB⊥BC,
∴∠ABC=90°,
∴∠ABD=∠EBC=∠DBE=30°,
在△BDE和△BCE中,
,
∴△BDE≌△BCE.(SAS).
(2)结论:四边形ABDE是菱形.
理由:∵△BDE≌△BCE,
∴DE=CE,
∵BE=CE,AB=EB,AD=EC,
∴AB=EB=DE=AD,
∴四边形ABED是菱形.
【点评】本题考查全等三角形的判定和性质、菱形的判定、旋转变换等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.
26.已知:如图,AD、BC相交于点O,OA=OD,AB∥CD.求证:AB=CD.
【分析】只要证明△AOB≌△DOC(ASA),即可解决问题.
【解答】证明:∵AB∥CD,
∴∠A=∠D
在△AOB和△DOC中,
,
∴△AOB≌△DOC(ASA).
∴AB=CD.
【点评】本题考查全等三角形的判定和性质、平行线的性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.
一.选择题(共10小题)
1.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.三角形 D.平行四边形
2.下列图形中有稳定性的是( )
A.正方形 B.直角三角形 C.长方形 D.平行四边形
3.下列叙述中错误的是( )
A.能够完全重合的图形称为全等图形
B.全等图形的形状和大小都相同
C.所有正方形都是全等图形
D.形状和大小都相同的两个图形是全等图形
4.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
A.90° B.135° C.150° D.180°
5.如图,两个三角形为全等三角形,则∠α的度数是( )
A.72° B.60° C.58° D.50°
6.如图,△ABO≌△DCO,∠D=80°,∠DOC=70°,则∠B=( )
A.35° B.30° C.25° D.20°
7.如图,AE∥FD,AE=FD,要使△EAC≌△FDB,需要添加下列选项中的( )
A.AB=BC B.EC=BF C.∠A=∠D D.AB=CD
8.如图,已知点B、E、C、F在同一直线上,且BE=CF,∠ABC=∠DEF,那么添加一个条件后.仍无法判定△ABC≌△DEF的是( )
A.AC=DF B.AB=DE C.AC∥DF D.∠A=∠D
9.不能使两个直角三角形全等的条件( )
A.一条直角边及其对角对应相等
B.斜边和一条直角边对应相等
C.斜边和一锐角对应相等
D.两个锐角对应相等
10.下列说法:①有两条直角边对应相等的两个直角三角形全等;②有斜边对应相等的两个等腰直角三角形全等;③有一条直角边和斜边上的高对应相等的两个直角三角形全等;④有一条边相等的两个等腰直角三角形全等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题)
11.工程建筑中经常采用三角形的结构,如屋顶钢架,其中的数学道理是 .
12.如图,六根木条钉成一个六边形框架ABCDEF,要使框架稳固且不活动,至少还需要添 根木条.
13.如图为4×4的正方形网格,图中的线段均为格点线段(线段的端点为格点),则∠1+∠2+∠3+∠4+∠5的度数为 .
14.由同一张底片冲洗出来的五寸照片和七寸照片 全等图形(填“是”或“不是”).
15.如图,△ABC≌△AED,若AB=AE,∠1=27°,则∠2= 度.
16.如图,△OAD≌△OBC,且OA=2,OC=6,则BD= .
17.如图,已知AB=AD,需要条件(用图中的字母表示) 可得△ABC≌△ADC,根据是 .
18.如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t= 秒时,△PEC与△QFC全等.
三.解答题(共8小题)
19.如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上,∠A=50°,∠F=40°.
(1)求△DBE各内角的度数;
(2)若AD=16,BC=10,求AB的长.
20.如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,求∠A的度数.
21.已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.
求证:△ABC≌△DEF.
22.如图,∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?
23.如图,已知CE⊥AB,DF⊥AB,AC=BD,CE=DF,求证:AC∥BD.
24.如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
25.如图,△BAD是由△BEC在平面内绕点B逆时针旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状.并说明理由.
26.已知:如图,AD、BC相交于点O,OA=OD,AB∥CD.求证:AB=CD.
2020年苏科新版八年级上册数学《第1章 全等三角形》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.三角形 D.平行四边形
【分析】根据三角形具有稳定性解答.
【解答】解:根据三角形具有稳定性,可得四个选项中只有直角三角形具有稳定性.
故选:C.
【点评】本题考查了三角形具有稳定性,是基础题,需熟记.
2.下列图形中有稳定性的是( )
A.正方形 B.直角三角形 C.长方形 D.平行四边形
【分析】根据三角形具有稳定性可得答案.
【解答】解:直角三角形有稳定性,
故选:B.
【点评】此题主要考查了三角形的稳定性,是需要识记的内容.
3.下列叙述中错误的是( )
A.能够完全重合的图形称为全等图形
B.全等图形的形状和大小都相同
C.所有正方形都是全等图形
D.形状和大小都相同的两个图形是全等图形
【分析】能够完全重合的两个图形叫做全等形,结合各选项进行判断即可.
【解答】解:A、能够重合的图形称为全等图形,说法正确,故本选项错误;
B、全等图形的形状和大小都相同,说法正确,故本选项错误;
C、所有正方形不一定都是全等图形,说法错误,故本选项正确;
D、形状和大小都相同的两个图形是全等图形,说法正确,故本选项错误;
故选:C.
【点评】本题考查了全等图形的知识,要求同学们掌握全等图形的定义及性质.
4.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
A.90° B.135° C.150° D.180°
【分析】标注字母,利用“边角边”判断出△ABC和△DEA全等,根据全等三角形对应角相等可得∠1=∠4,然后求出∠1+∠3=90°,再判断出∠2=45°,然后计算即可得解.
【解答】解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠1=∠4,
∵∠3+∠4=90°,
∴∠1+∠3=90°,
又∵∠2=45°,
∴∠1+∠2+∠3=90°+45°=135°.
故选:B.
【点评】本题考查了全等图形,网格结构,准确识图判断出全等的三角形是解题的关键.
5.如图,两个三角形为全等三角形,则∠α的度数是( )
A.72° B.60° C.58° D.50°
【分析】根据三角形内角和定理计算出∠1的度数,然后再根据全等三角形的对应角相等可得∠α=∠1=72°.
【解答】解:根据三角形内角和可得∠1=180°﹣50°﹣58°=72°,
因为两个全等三角形,
所以∠α=∠1=72°,
故选:A.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应角相等.
6.如图,△ABO≌△DCO,∠D=80°,∠DOC=70°,则∠B=( )
A.35° B.30° C.25° D.20°
【分析】根据三角形内角和定理求出∠C,根据全等三角形的性质解答即可.
【解答】解:∵∠D=80°,∠DOC=70°,
∴∠C=180°﹣∠D﹣∠DOC=30°,
∵△ABO≌△DCO,
∴∠B=∠C=30°,
故选:B.
【点评】本题考查的是全等三角形的性质、三角形内角和定理,掌握全等三角形的对应角相等是解题的关键.
7.如图,AE∥FD,AE=FD,要使△EAC≌△FDB,需要添加下列选项中的( )
A.AB=BC B.EC=BF C.∠A=∠D D.AB=CD
【分析】添加条件AB=CD可证明AC=BD,然后再根据AE∥FD,可得∠A=∠D,再利用SAS定理证明△EAC≌△FDB即可.
【解答】解:∵AE∥FD,
∴∠A=∠D,
∵AB=CD,
∴AC=BD,
在△AEC和△DFB中,
∴△EAC≌△FDB(SAS),
故选:D.
【点评】此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
8.如图,已知点B、E、C、F在同一直线上,且BE=CF,∠ABC=∠DEF,那么添加一个条件后.仍无法判定△ABC≌△DEF的是( )
A.AC=DF B.AB=DE C.AC∥DF D.∠A=∠D
【分析】根据全等三角形的判定方法逐项判断即可.
【解答】解:
∵BE=CF,
∴BE+EC=EC+CF,即BC=EF,且∠ABC=∠DEF,
∴当AC=DF时,满足SSA,无法判定△ABC≌△DEF,故A不能;
当AB=DE时,满足SAS,可以判定△ABC≌△DEF,故B可以;
当AC∥DF时,可得∠ACB=∠F,满足ASA,可以判定△ABC≌△DEF,故C可以;
当∠A=∠D时,满足AAS,可以判定△ABC≌△DEF,故D可以;
故选:A.
【点评】本题主要考查全等三角形的判定方法,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.
9.不能使两个直角三角形全等的条件( )
A.一条直角边及其对角对应相等
B.斜边和一条直角边对应相等
C.斜边和一锐角对应相等
D.两个锐角对应相等
【分析】根据各选项提供的已知条件,结合直角三角形全等的判定方法,对选项逐一验证,选项D只有两个锐角对应相等是不符合直角三角形判定方法的,所以不能判定三角形全等.
【解答】解:A、符合AAS,正确;
B、符合HL,正确;
C、符合ASA,正确;
D、因为判定三角形全等必须有边的参与,错误.
故选:D.
【点评】此题主要考查全等三角形的判定方法的掌握情况.判断全等时必须要有边对应相等的关系.
10.下列说法:①有两条直角边对应相等的两个直角三角形全等;②有斜边对应相等的两个等腰直角三角形全等;③有一条直角边和斜边上的高对应相等的两个直角三角形全等;④有一条边相等的两个等腰直角三角形全等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据判定两直角三角形全等的判定方法进行判断即可.
【解答】解:①有两条直角边对应相等的两个直角三角形全等,可利用SAS判定两直角三角形全等;
②有斜边对应相等的两个等腰直角三角形全等,可利用ASA判定两直角三角形全等;
③有一条直角边和斜边上的高对应相等的两个直角三角形全等,能判定两直角三角形全等;
④有一条边相等的两个等腰直角三角形全等,不能判定两直角三角形全等.
故选:C.
【点评】本题考查了直角三角形全等的判定方法,直角三角形首先是三角形,所以一般三角形全等的判定方法都适合它,同时,直角三角形又是特殊的三角形,有它的特殊性,作为“HL”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
二.填空题(共8小题)
11.工程建筑中经常采用三角形的结构,如屋顶钢架,其中的数学道理是 三角形具有稳定性 .
【分析】根据三角形具有稳定性解答即可.
【解答】解:工程建筑中经常采用三角形的结构,如屋顶钢架,其中的数学道理是三角形具有稳定性,
故答案为:三角形具有稳定性.
【点评】此题主要考查了三角形的稳定性,是需要记忆的内容.
12.如图,六根木条钉成一个六边形框架ABCDEF,要使框架稳固且不活动,至少还需要添 3 根木条.
【分析】根据三角形的稳定性,只要使六边形框架ABCDEF变成三角形的组合体即可.
【解答】解:根据三角形的稳定性,得
如图:从图中可以看出,要使框架稳固且不活动,至少还需要添3根木条.
【点评】本题主要考查的是三角形的稳定性.
13.如图为4×4的正方形网格,图中的线段均为格点线段(线段的端点为格点),则∠1+∠2+∠3+∠4+∠5的度数为 225° .
【分析】根据正方形的性质可得出∠3=45°,根据长方形的性质即可得出相等的边,由此可得出全等的三角形,进而得出∠1与∠5互余、∠2与∠4互余,再将其代入∠1+∠2+∠3+∠4+∠5中即可得出结论.
【解答】解:在图中标上字母,如图所示.
∵四边形ABCD为4×4的正方形,
∴∠3=45°.
∵四边形ANPE为1×1的正方形,
∴AE=AN.
∵四边形CDEF和四边形BCMN均为4×3的长方形,
∴CE=CN.
在△ACE和△ACN中,,
∴△ACE≌△ACN(SSS),
∴∠AEC=∠ANC,
∴∠2+∠4+90°=180°,
∴∠2与∠4互余.
同理可得:∠1与∠5互余.
∴∠1+∠2+∠3+∠4+∠5=(∠1+∠5)+(∠2+∠4)+∠3=90°+90°+45°=225°.
故答案为:225°.
【点评】本题考查了全等图形、全等三角形的判定与性质、长方形及正方形的性质,解题的关键是找出∠3=45°、∠1与∠5互余、∠2与∠4互余.
14.由同一张底片冲洗出来的五寸照片和七寸照片 不是 全等图形(填“是”或“不是”).
【分析】能够完全重合的两个图形叫做全等形,图形重合的是全等形,不重合的不是全等形.
【解答】解:由全等形的概念可知:由同一张底片冲洗出来的五寸照片和七寸照片,大小不一样,所以不是全等图形.
故答案为:不是.
【点评】本题考查了全等形的概念,判定是不是全等形主要看图形是不是能够重合.
15.如图,△ABC≌△AED,若AB=AE,∠1=27°,则∠2= 27 度.
【分析】先运用三角形全等求出∠BAC=∠EAD,则∠2易求.
【解答】解:∵△ABC≌△AED,AB=AE,
∴∠BAC=∠EAD
∴∠2=∠1=27°.
【点评】本题考查了全等三角形的性质;全等三角形的对应边相等,对应角相等,是需要识记的内容,找准对应角是解题的关键.
16.如图,△OAD≌△OBC,且OA=2,OC=6,则BD= 4 .
【分析】根据全等三角形的性质可得DO=CO=6,BO=AO=2,再利用线段的和差关系可得答案.
【解答】解:∵△OAD≌△OBC,
∴DO=CO=6,BO=AO=2,
∴BD=6﹣2=4,
故答案为:4.
【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等.
17.如图,已知AB=AD,需要条件(用图中的字母表示) BC=DC 可得△ABC≌△ADC,根据是 SSS .
【分析】添加条件BC=DC,可直接利用SSS定理判定△ABC≌△ADC.
【解答】解:添加条件BC=DC,
∵在△ABC和△ADC中,
∴△ABC≌△ADC(SSS),
故答案为:BC=DC;SSS.
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
18.如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t= 1或或12 秒时,△PEC与△QFC全等.
【分析】根据题意化成三种情况,根据全等三角形的性质得出CP=CQ,代入得出关于t的方程,求出即可.
【解答】解:分为三种情况:①如图1,P在AC上,Q在BC上,
∵PE⊥l,QF⊥l,
∴∠PEC=∠QFC=90°,
∵∠ACB=90°,
∴∠EPC+∠PCE=90°,∠PCE+∠QCF=90°,
∴∠EPC=∠QCF,
则△PCE≌△CQF,
∴PC=CQ,
即6﹣t=8﹣3t,
t=1;
②如图2,P在BC上,Q在AC上,
∵由①知:PC=CQ,
∴t﹣6=3t﹣8,
t=1;
t﹣6<0,即此种情况不符合题意;
③当P、Q都在AC上时,如图3,
CP=6﹣t=3t﹣8,
t=;
④当Q到A点停止,P在BC上时,AC=PC,t﹣6=6时,解得t=12.
P和Q都在BC上的情况不存在,∵P的速度是每秒1cm,Q的速度是每秒3cm;
故答案为:1或或12.
【点评】本题考查了全等三角形的判定和性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等.
三.解答题(共8小题)
19.如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上,∠A=50°,∠F=40°.
(1)求△DBE各内角的度数;
(2)若AD=16,BC=10,求AB的长.
【分析】(1)根据全等三角形的性质求出∠D、∠E,根据三角形内角和定理求出∠EBD即可;
(2)根据全等三角形的性质得出AC=BD,求出AB=CD,即可求出答案.
【解答】解:(1)∵△ACF≌△DBE,∠A=50°,∠F=40°,
∴∠D=∠A=50°,∠E=∠F=40°,
∴∠EBD=180°﹣∠D﹣∠E=90°;
(2)∵△ACF≌△DBE,
∴AC=BD,
∴AC﹣BC=DB﹣BC,
∴AB=CD,
∵AD=16,BC=10,
∴AB=CD=(AD﹣BC)=3.
【点评】本题考查了全等三角形的性质的应用,能熟记全等三角形的性质是解此题的关键,注意:全等三角形的对应角相等,对应边相等.
20.如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,求∠A的度数.
【分析】根据全等三角形对应边相等可得OB=OD,全等三角形对应角相等可得∠ABO=∠D,再根据等边对等角求出∠OBD=∠D,然后求出∠ABC,再根据两直线平行,内错角相等解答即可.
【解答】解:∵△ABO≌△CDO,
∴OB=OD,∠ABO=∠D,
∴∠OBD=∠D=(180°﹣∠BOD)=×(180°﹣30)=75°,
∴∠ABC=180°﹣75°×2=30°,
∴∠A=∠ABC=30°.
【点评】本题考查了全等三角形的性质,等边对等角的性质,平行线的性质,熟记性质并准确识图是解题的关键.
21.已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.
求证:△ABC≌△DEF.
【分析】直接利用全等三角形的判定方法得出答案.
【解答】证明:∵AB∥DE,
∴∠B=∠DEF
∵BE=FC,
∴BC=EF,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
【点评】此题主要考查了全等三角形的判定,全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.
22.如图,∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?
【分析】根据∠CAE=∠BAD,可得∠CAB=∠EAD,又已知∠B=∠D,AC=AE,可利用AAS证明△ABC≌△ADE.
【解答】解:△ABC≌△ADE.
∵∠CAE=∠BAD,
∴∠CAB=∠EAD,
在△ABC和△ADE,
∵,
∴△ABC≌△ADE(AAS).
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
23.如图,已知CE⊥AB,DF⊥AB,AC=BD,CE=DF,求证:AC∥BD.
【分析】利用已知条件可直接证出Rt△ACE≌Rt△BDF(HL),可得到对应角∠A=∠B,根据内错角相等,两直线平行可证得AC∥BD.
【解答】证明:∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°.
又∵AC=BD,CE=DF,
∴Rt△ACE≌Rt△BDF(HL).
∴∠A=∠B,
∴AC∥BD.
【点评】本题考查了全等三角形的判定和性质以及平行线的判定定理等知识.
24.如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
【分析】本题要分情况讨论:①Rt△APQ≌Rt△CBA,此时AP=BC=5cm,可据此求出P点的位置.
②Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合.
【解答】解:根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=5cm;
②当P运动到与C点重合时,AP=AC,
在Rt△ABC与Rt△QPA中,
,
∴Rt△QAP≌Rt△BCA(HL),
即AP=AC=10cm,
∴当点P与点C重合时,△ABC才能和△APQ全等.
综上所述,当P运动到AP=BC、点P与点C重合时,△ABC才能和△APQ全等.
【点评】本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.
25.如图,△BAD是由△BEC在平面内绕点B逆时针旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状.并说明理由.
【分析】(1)根据SAS即可证明△BDE≌△BCE.
(2)根据四边相等的四边形是菱形即可判定.
【解答】解:(1)证明:∵由旋转可知,AB=EB,AD=EC,BD=BC,∠ABD=∠EBC,∠ABE=∠DBC=60°,
∵AB⊥BC,
∴∠ABC=90°,
∴∠ABD=∠EBC=∠DBE=30°,
在△BDE和△BCE中,
,
∴△BDE≌△BCE.(SAS).
(2)结论:四边形ABDE是菱形.
理由:∵△BDE≌△BCE,
∴DE=CE,
∵BE=CE,AB=EB,AD=EC,
∴AB=EB=DE=AD,
∴四边形ABED是菱形.
【点评】本题考查全等三角形的判定和性质、菱形的判定、旋转变换等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.
26.已知:如图,AD、BC相交于点O,OA=OD,AB∥CD.求证:AB=CD.
【分析】只要证明△AOB≌△DOC(ASA),即可解决问题.
【解答】证明:∵AB∥CD,
∴∠A=∠D
在△AOB和△DOC中,
,
∴△AOB≌△DOC(ASA).
∴AB=CD.
【点评】本题考查全等三角形的判定和性质、平行线的性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
