【2020届】高考数学圆锥曲线专题复习:圆锥曲线几何性质精华
文档属性
| 名称 | 【2020届】高考数学圆锥曲线专题复习:圆锥曲线几何性质精华 | 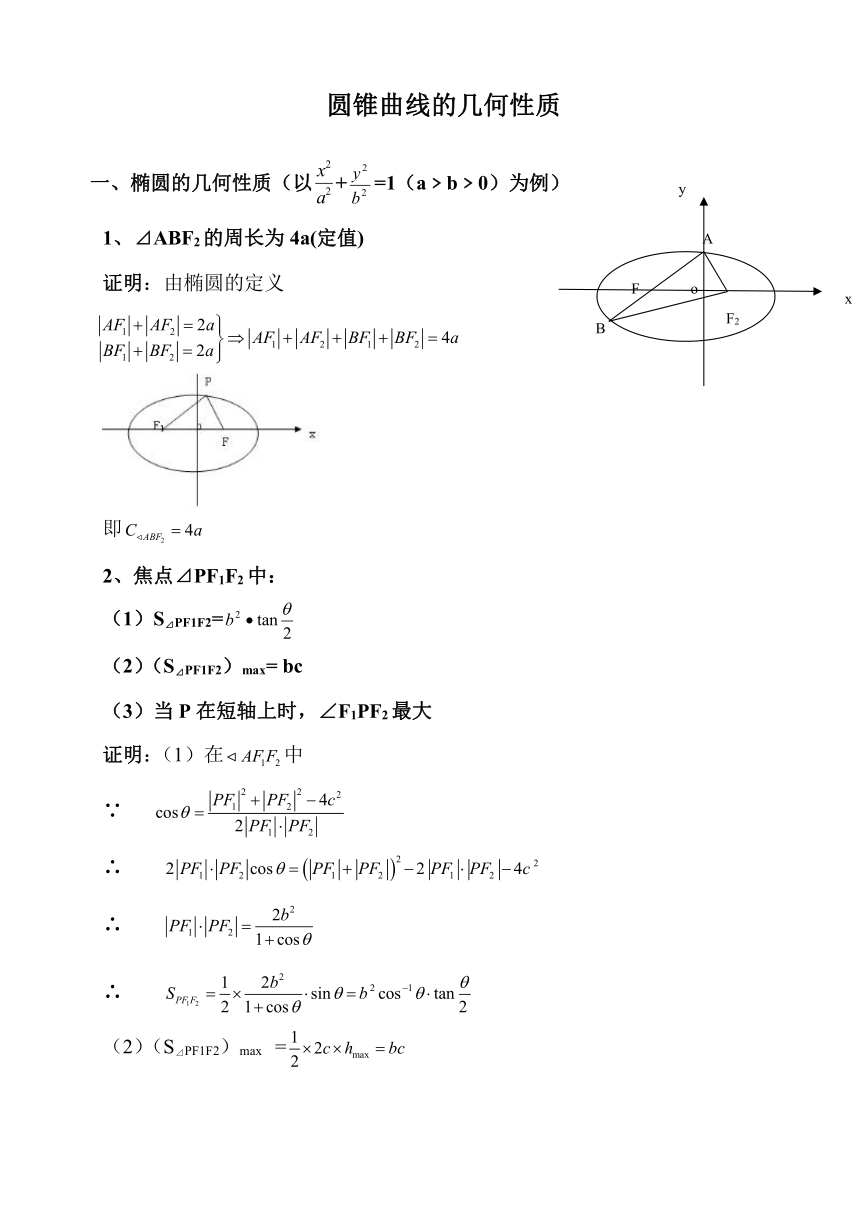 | |
| 格式 | zip | ||
| 文件大小 | 184.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 14:14:57 | ||
图片预览





文档简介
圆锥曲线的几何性质
一、椭圆的几何性质(以+=1(a﹥b﹥0)为例)
1、⊿ABF2的周长为4a(定值)
证明:由椭圆的定义
即
2、焦点⊿PF1F2中:
(1)S⊿PF1F2=
(2)(S⊿PF1F2)max= bc
(3)当P在短轴上时,∠F1PF2最大
证明:(1)在中
∵
∴
∴
∴
(2)(S⊿PF1F2)max =
(3
当=0时 有最小值 即∠F1PF2最大
3、 过点F1作⊿PF1F2的∠P的外角平分线的垂线,垂足为M ,则M 的轨迹是x2+y2=a2
证明:延长交于,连接
由已知有 为中点
∴ ==
所以M的轨迹方程为 。
4、以椭圆的任意焦半径为直径的圆,都与圆x2+y2=a2内切
证明:取的中点,连接。令圆的直径,半径为
∵ =
∴ 圆与圆内切
∴ 以椭圆的任意焦半径为直径的圆,都与圆x2+y2=a2内切。
5、任一焦点⊿PF1F2的内切圆圆心为I,连结PI延长交长轴于R,
则 ∣IR∣:∣IP∣=e
证明:证明:连接由三角形内角角平分线性质有
∵
∴
6、以任一焦点弦为直径的圆与相应准线相离。
证明:令到准线的距离为
以为直径的圆的圆心为到准线的距离为。
∵
∵
∵ ,∴,∴以任一焦点弦为直径的圆与相应准线相离
7、A为椭圆内一定点,P在椭圆上,则:
(∣PA∣+∣PF2∣)max =2a+∣AF1∣
(∣PA∣+∣PF2∣)min =2a-∣AF1∣
证明:连接
∵
∵
∴
∴ (∣PA∣+∣PF2∣)max =2a+∣AF1∣
(∣PA∣+∣PF2∣)min =2a-∣AF1∣
8、A 为椭圆内一定点,P是椭圆上的动点,则
(∣PA∣+)min = A到右准线的距离
证明:设到右准线的距离d,由椭圆的第二定义有
∴(∣PA∣+)min = = A到右准线的距离.
9、焦点⊿PF1F2的旁心在直线 x=±a 上。
证明:令☉I与⊿PF1F2三边所在的直线相切于M、N、A
∵ ,
∴
∵ ,∴ ,∵
∴ ,∵ ,∴
∴ 即为椭圆顶点。∴ 焦点⊿PF1F2的旁心在直线x=±a上。
10、P是椭圆上任意一点,PF2的延长线交右准线于E,K是准线
上另一任意点,连结PK交椭圆于Q,则KF2平分∠EF2Q
证明:令P,Q到准线的距离为
由三角形外角平分线性质定理有KF2平分∠EF2Q
11、
证明:令
当的斜率存在时,设直线方程为
∵
∴
∴
=
当的斜率存在时,,∴。
12、AB是椭圆的任意一弦,P是AB中点,
则(定值)
证明:令 ,
则
∵ ,
∵ ,,∴ ,∴ 。
13、椭圆的短轴端点为B1、B2,P是椭圆上任一点,连结B1P、B2P分别
交长轴于N、M两点,则有∣OM∣*∣ON∣=a2
证明:
∴
∵ 由于、、共线
∴
∵ 由于、、N共线,
∴ ,∴
∵ ,∴ 。
14、椭圆的长轴端点为A1、A 2,P是椭圆上任一点,
连结A1P、A2P并延长,交一准线于N、M两点,
则M、N与对应准线的焦点张角为900
证明:令,,
∴
∵ 由于、、共线 ,∴
∵ 由于共线 ,∴
∴ ,∵
∴ ,∵
∴ ,∴ M、N与对应准线的焦点张角为900
15、过椭圆准线上任一点作椭圆和切线,切点弦AB过
该准线对应的焦点。
证明:设,则的方程为
即 必过点
16、椭圆的光学性质:过一焦点的光线经椭圆反射后必过另一焦点。
证明:设,则过点的切线:,直线的法线交轴于
直线的法向量为:
∵
∴
同理 ,∵
同理,
∴ ,
∴ ,即过一焦点的光线经椭圆反射后必过另一焦点。
二、双曲线的几何性质(均以 为例)
(1)焦点三角形面积:
(2) 过作∠F1PF2的内角平行线的重线垂足M的轨迹是
(3) 以焦半径为直径作圆长的焦半径为直径作圆与内切,小的圆与外切。
(4)以焦点为直径作圆与该焦点对应准线相交
(5)焦点⊿PF1F2的内切圆心横生标为±a即与实轴的切点一定是实轴端点
(6)焦点弦为直径的圆被相应准线截得圆弧所对的圆心角为定值∠MCN=2arccos
(7) A为双曲线内一定点P为双曲线上动点=+=-2a
(8) 如图:A为双曲线内一定点,P是双曲线上的动点,+等于A到右准线的距离
(9)焦点到渐近线的距离等于b
(10)双曲线上的任上点到两渐近线的距离之积等于定值
(11)P是弦AB中点K.K=定值
(12)P为双线上任一点过P点作两渐近线的平行线与渐近线围成的平行四边形面积等于定值ab
(13) 过P的切线平分∠F1PF2(光学性质)即经过一焦点的光线被双曲线反射,反射光线的下长线过另一焦点
(14)双曲线与渐近线把平面分成5部分
双曲线上的点
渐近线上的点
区域①的点
区域②的点
区域③的点
过渐近线上的点(除中心)只能作一条切线,过中心无切线,没有与两支都相切的切线过区域①的点作切线分别在两支上,过区域③的点作切线切点在同一支上,过区域②的点没切线,双曲线的切线斜率,区域①、②的点可作弦的中点,中心是任意过中心的弦的中点,渐近线上(除中心),双曲线上,区域③的点不可能是弦中点。
(15)直线L与双曲线的渐近线
交于A、B两点,与双曲线交于C、D两点,则AC=BD
三、抛物线的几何性质
均以抛物线为例
如图:A为抛物线内一定点,P是抛物线上的动点,
+等于A到准线的距离。
(2) 过抛物线焦点F作弦AB,其中A(x1,y1),B(x2,y2)则有:
①
②
③
④
⑤
⑥以AB为直径的圆与准线相切
(3)过抛物线顶点作任意互相垂直的弦
OA、OB,则弦AB必过定点(2p,0);反之亦成立,
即过定点(2p,0)作直线交抛物线于A、B两点,
则有OA垂直OB
(4)过抛物线焦点F作直线交抛物线于P、Q两点,弦PQ的垂直平分线交抛物线的对称轴于R,则
(5)过抛物线H上任一点P(X0,Y0)的切线方程为
一、椭圆的几何性质(以+=1(a﹥b﹥0)为例)
1、⊿ABF2的周长为4a(定值)
证明:由椭圆的定义
即
2、焦点⊿PF1F2中:
(1)S⊿PF1F2=
(2)(S⊿PF1F2)max= bc
(3)当P在短轴上时,∠F1PF2最大
证明:(1)在中
∵
∴
∴
∴
(2)(S⊿PF1F2)max =
(3
当=0时 有最小值 即∠F1PF2最大
3、 过点F1作⊿PF1F2的∠P的外角平分线的垂线,垂足为M ,则M 的轨迹是x2+y2=a2
证明:延长交于,连接
由已知有 为中点
∴ ==
所以M的轨迹方程为 。
4、以椭圆的任意焦半径为直径的圆,都与圆x2+y2=a2内切
证明:取的中点,连接。令圆的直径,半径为
∵ =
∴ 圆与圆内切
∴ 以椭圆的任意焦半径为直径的圆,都与圆x2+y2=a2内切。
5、任一焦点⊿PF1F2的内切圆圆心为I,连结PI延长交长轴于R,
则 ∣IR∣:∣IP∣=e
证明:证明:连接由三角形内角角平分线性质有
∵
∴
6、以任一焦点弦为直径的圆与相应准线相离。
证明:令到准线的距离为
以为直径的圆的圆心为到准线的距离为。
∵
∵
∵ ,∴,∴以任一焦点弦为直径的圆与相应准线相离
7、A为椭圆内一定点,P在椭圆上,则:
(∣PA∣+∣PF2∣)max =2a+∣AF1∣
(∣PA∣+∣PF2∣)min =2a-∣AF1∣
证明:连接
∵
∵
∴
∴ (∣PA∣+∣PF2∣)max =2a+∣AF1∣
(∣PA∣+∣PF2∣)min =2a-∣AF1∣
8、A 为椭圆内一定点,P是椭圆上的动点,则
(∣PA∣+)min = A到右准线的距离
证明:设到右准线的距离d,由椭圆的第二定义有
∴(∣PA∣+)min = = A到右准线的距离.
9、焦点⊿PF1F2的旁心在直线 x=±a 上。
证明:令☉I与⊿PF1F2三边所在的直线相切于M、N、A
∵ ,
∴
∵ ,∴ ,∵
∴ ,∵ ,∴
∴ 即为椭圆顶点。∴ 焦点⊿PF1F2的旁心在直线x=±a上。
10、P是椭圆上任意一点,PF2的延长线交右准线于E,K是准线
上另一任意点,连结PK交椭圆于Q,则KF2平分∠EF2Q
证明:令P,Q到准线的距离为
由三角形外角平分线性质定理有KF2平分∠EF2Q
11、
证明:令
当的斜率存在时,设直线方程为
∵
∴
∴
=
当的斜率存在时,,∴。
12、AB是椭圆的任意一弦,P是AB中点,
则(定值)
证明:令 ,
则
∵ ,
∵ ,,∴ ,∴ 。
13、椭圆的短轴端点为B1、B2,P是椭圆上任一点,连结B1P、B2P分别
交长轴于N、M两点,则有∣OM∣*∣ON∣=a2
证明:
∴
∵ 由于、、共线
∴
∵ 由于、、N共线,
∴ ,∴
∵ ,∴ 。
14、椭圆的长轴端点为A1、A 2,P是椭圆上任一点,
连结A1P、A2P并延长,交一准线于N、M两点,
则M、N与对应准线的焦点张角为900
证明:令,,
∴
∵ 由于、、共线 ,∴
∵ 由于共线 ,∴
∴ ,∵
∴ ,∵
∴ ,∴ M、N与对应准线的焦点张角为900
15、过椭圆准线上任一点作椭圆和切线,切点弦AB过
该准线对应的焦点。
证明:设,则的方程为
即 必过点
16、椭圆的光学性质:过一焦点的光线经椭圆反射后必过另一焦点。
证明:设,则过点的切线:,直线的法线交轴于
直线的法向量为:
∵
∴
同理 ,∵
同理,
∴ ,
∴ ,即过一焦点的光线经椭圆反射后必过另一焦点。
二、双曲线的几何性质(均以 为例)
(1)焦点三角形面积:
(2) 过作∠F1PF2的内角平行线的重线垂足M的轨迹是
(3) 以焦半径为直径作圆长的焦半径为直径作圆与内切,小的圆与外切。
(4)以焦点为直径作圆与该焦点对应准线相交
(5)焦点⊿PF1F2的内切圆心横生标为±a即与实轴的切点一定是实轴端点
(6)焦点弦为直径的圆被相应准线截得圆弧所对的圆心角为定值∠MCN=2arccos
(7) A为双曲线内一定点P为双曲线上动点=+=-2a
(8) 如图:A为双曲线内一定点,P是双曲线上的动点,+等于A到右准线的距离
(9)焦点到渐近线的距离等于b
(10)双曲线上的任上点到两渐近线的距离之积等于定值
(11)P是弦AB中点K.K=定值
(12)P为双线上任一点过P点作两渐近线的平行线与渐近线围成的平行四边形面积等于定值ab
(13) 过P的切线平分∠F1PF2(光学性质)即经过一焦点的光线被双曲线反射,反射光线的下长线过另一焦点
(14)双曲线与渐近线把平面分成5部分
双曲线上的点
渐近线上的点
区域①的点
区域②的点
区域③的点
过渐近线上的点(除中心)只能作一条切线,过中心无切线,没有与两支都相切的切线过区域①的点作切线分别在两支上,过区域③的点作切线切点在同一支上,过区域②的点没切线,双曲线的切线斜率,区域①、②的点可作弦的中点,中心是任意过中心的弦的中点,渐近线上(除中心),双曲线上,区域③的点不可能是弦中点。
(15)直线L与双曲线的渐近线
交于A、B两点,与双曲线交于C、D两点,则AC=BD
三、抛物线的几何性质
均以抛物线为例
如图:A为抛物线内一定点,P是抛物线上的动点,
+等于A到准线的距离。
(2) 过抛物线焦点F作弦AB,其中A(x1,y1),B(x2,y2)则有:
①
②
③
④
⑤
⑥以AB为直径的圆与准线相切
(3)过抛物线顶点作任意互相垂直的弦
OA、OB,则弦AB必过定点(2p,0);反之亦成立,
即过定点(2p,0)作直线交抛物线于A、B两点,
则有OA垂直OB
(4)过抛物线焦点F作直线交抛物线于P、Q两点,弦PQ的垂直平分线交抛物线的对称轴于R,则
(5)过抛物线H上任一点P(X0,Y0)的切线方程为
同课章节目录
