人教版 八年级数学上册 15.3分式方程之解分式方程专项练习(含解析)
文档属性
| 名称 | 人教版 八年级数学上册 15.3分式方程之解分式方程专项练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 146.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-05 21:43:29 | ||
图片预览

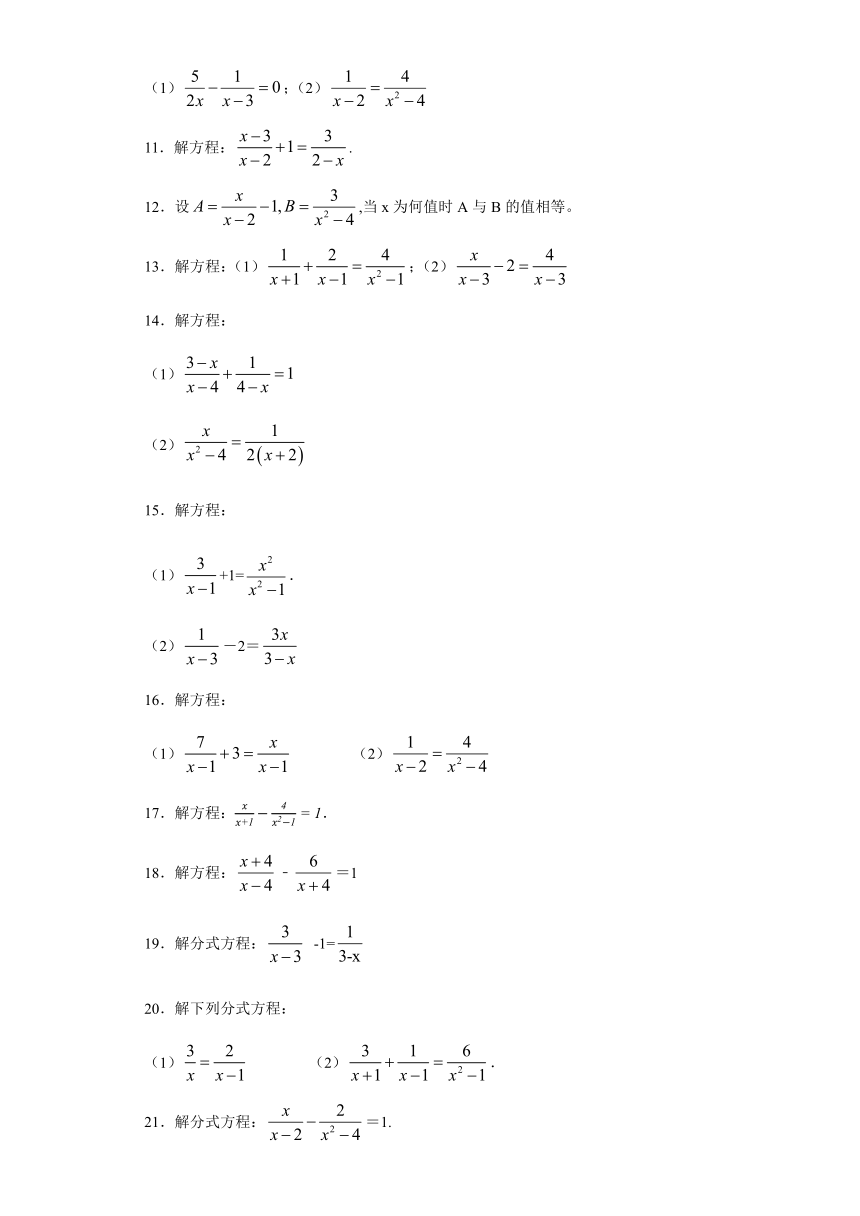



文档简介
八年级上册人教版 15.3分式方程之解分式方程专项
一、解答题
1.解分式方程
(1)
(2)
2.解方程:
3.解方程:
4
??
2
?2??
?
??
2???
=1.
4.解方程:;
5.解分式方程:
6.解下列分式方程:
(1)
(2)
7.(1)解方程:
(2)已知关于的方程 的解是正数,求的取值范围.
8.解方程:
9.解方程:=1.
10.解方程:
(1);(2)
11.解方程:.
12.设,当x为何值时A与B的值相等。
13.解方程:(1);(2)
14.解方程:
(1)
(2)
15.解方程:
(1)+1=.
(2)-2=
16.解方程:
(1) (2)
17.解方程:
??
??+1
?
4
??
2
?1
=1.
18.解方程:﹣=1
19.解分式方程: -1=
20.解下列分式方程:
(1) (2).
21.解分式方程:=1.
22.解方程:+=1
23.解方程:.
24.阅读理解:
关于x的方程:x+=c+的解为x1=c,x2=;x﹣=c﹣(可变形为x+=c+)的解为x1=c,x2=;x+=c+的解为x1=c,x2= Zx+=c+的解为x1=c,x2=Z.
(1)归纳结论:根据上述方程与解的特征,得到关于x的方程x+=c+(m≠0)的解为 .
(2)应用结论:解关于y的方程y﹣a=﹣
参考答案
1.(1)无解;(2)x=6.
【解析】
(1)
去分母得,
去括号得,,
移项合并得,3x=3
解得,x=1,
经检验,x=1是增根,原方程无解;
(2)
去分母得,,
去括号得,
移项合并得,x=6,
经检验,x=6是原方程的解.
2..
【解析】
解:方程两边同时乘以,得
解这个方程,得.
经检验:是原方程的根,
∴原方程的解是:.
3.??=?2.
【解析】
4+
??
2
=??(???2),
2??=?4,
??=?2.
经检验:??=?2是原方程的解.
∴原方程的解为??=?2.
4.原方程无解.
【解析】
解:去分母得:,
解得,
经检验是增根,舍去
所以,原方程无解.
5..
【解析】
解:原方程即为:,
方程两边同时乘以,得,
解这个方程,得.
经检验:是原方程的解,所以原方程的解是.
6.(1);(2)
【解析】
解:(1)去分母得:3x-3=2x, 解得:x=3, 经检验x=3是分式方程的解; (2)去分母得:x-3+x-2=-3,
解得:x=1, 经检验x=1是分式方程的解;
7.(1)x= -(2)m>-6且m≠-4
【解析】
解:(1)?1=
两边都乘(x+2)(x?2),得
x(x+2)?(x+2)(x?2)=1,
解得x=?,
检验:当x=?时,(x+2)(x?2)=?≠0,
∴原分式方程的解为x=?;
(2)=3
去分母,得2x+m=3(x?2),
去括号,得2x+m=3x?6,
解得:x=m+6,
根据题意得:m+6?2≠0且m+6>0,
解得:m>?6且m≠?4.
故答案是:(1) x=?;(2)m>?6且m≠?4.
8.
【解析】
解:
方程两边同乘以得
去括号的
移项得
合并得
系数
检验:当时,
∴原分式方程的解为
9.x=1
【解析】
去分母得:x(x﹣2)﹣2=x2﹣4,
解得:x=1,
经检验x=1是分式方程的解.
10.(1)x=5是原方程的解;(2)原方程无解.
【解析】
(1)解:两边乘以最简公分母,得
,
即,
解得:x=5,
检验:把x=5代入最简公分母原 ,
因此x=5是原方程的解.
(2)解:方程两边同乘最简公分母得
x+2=4,
解得:x=2,
检验:把x=2代入最简公分母中,=(2+2)(2-2)=0,
故x=2是原方程的增根,所以原方程且无解.
11..
【解析】
解分式方程去分母转化成一元一次方程,分式方程一定要检验
12.当x=时,A与B的值相等
【解析】
整体分析:
由题意得分式方程,解这个分式,注意需要验根.
解:由A=B,得,
方程两边都乘以(x-2)(x+2),去分母得x(x+2)-x2+4=3,
解得x=.
经检验x=是原方程的解.
所以当x=时,A与B的值相等.
13.(1)无解;(2).
【解析】
解:(1)方程两边同时乘以,得,
解这个方程,得.
经检验是原方程的增根,所以原方程无解.
(2)方程两边同时乘以,得,
解这个方程,得.
经检验是原方程的根,所以原方程的解是.
14.(1);(2)无解
【解析】
(1)去分母得:3?x?1=x?4,
解得:x=3,
经检验x=3是分式方程的解;
(2)
去分母得:2x=x-2,
解得:x=-2,
经检验x=-2是分式方程增根,故原方程无解.
15.(1);(2)x=-7
【解析】
(1)+1=,
两边都乘以(x+1)(x-1),得
3(x+1)+ (x+1)(x-1)=x2,
解之得
,
检验:当时,(x+1)(x-1) ≠0,
∴是原方程的根;
(2)-2=,
两边都乘以 (x-3),得
1-2(x-3)=-3x,
解之得
x=-7,
检验:当x=-7时,x-3 ≠0,
∴x=-7是原方程的根.
16.(1)2;(2)无解
【解析】
解::(1)去分母得:7+3(x-1)=x, 去括号得:7+3x-3=x, 移项合并得:2x=-4, 解得:x=-2, 经检验x=-2是分式方程的解;
(2)去分母得:x+2=4, 移项合并得:x=2, 解得:x=2, 经检验x=2是增根,分式方程无解.
17.x=﹣3.
【解析】
首先去掉分母,观察可得最简公分母是
??
2
?1,方程两边乘最简公分母,可以把分式方程转化为整式方程求解,然后解一元一次方程,最后检验即可求解.
试题解析:方程两边同乘以
??
2
?1,得??(???1)?4=
??
2
?1,
解得??=?3.
经检验,??=?3是原方程的根.
∴原方程的解为??=?3.
18.x=﹣28
【解析】
解:去分母,得(x+4)2﹣6(x﹣4)=(x﹣4)(x+4)
去括号,得x2+8x+16﹣6x+24=x2﹣16
移项,合并同类项,得2x=﹣56
系数化为1,得x=﹣28
检验:当x=﹣28时,(x﹣4)(x+4)≠0,
所以原方程的解是x=﹣28.
19.7
【解析】
-1=
3-(x-3)=-1
3-x+3=-1
x=7
20.(1)x=3;(2)x=2
【解析】
解:(1)两边都乘以最简公分母x(x-1),得: 3(x-1)=2x, 去括号得:3x-3=2x, 解得: x=3, 经检验x=3是原分式方程的解;
(1)两边都乘以最简公分母(x+1)(x-1),得: 3(x-1)+(x+1)=6, 去括号得:3x-3+x+1=6, 解得: x=2, 经检验x=2是原分式方程的解.
故答案为(1)x=3;(2)x=2.
21.X=-1
【解析】
去分母得x(x+2)-2=(x+2)(x-2), 解得x=-1, 检验:当x=-1时,(x+2)(x-2) ≠0, 所以原方程的解为x=-1. 故答案为x=-1.
22.x = 1
【解析】
【详解】
方程两边乘(x-2)得:
3x - 4 = x-2,
解得:x = 1
检验:当x=1时,x-2≠0,
∴x=1是原方程的解.
23.x=1.
【解析】
方程两边都乘(2x-3),得
x-5=4(2x-3),
解得x=1.
检验:当x=1时,2x-3≠0.
∴原方程的根是x=1.
24.(1)x1=c,x2=;(2)y1=a,y2=.
【解析】
解:(1)仿照题意得:方程解为x1=c,x2=;
故答案为:x1=c,x2=;
(2)方程变形得:y﹣1+=a﹣1+,
∴y﹣1=a﹣1或y﹣1=,
解得:y1=a,y2=.
一、解答题
1.解分式方程
(1)
(2)
2.解方程:
3.解方程:
4
??
2
?2??
?
??
2???
=1.
4.解方程:;
5.解分式方程:
6.解下列分式方程:
(1)
(2)
7.(1)解方程:
(2)已知关于的方程 的解是正数,求的取值范围.
8.解方程:
9.解方程:=1.
10.解方程:
(1);(2)
11.解方程:.
12.设,当x为何值时A与B的值相等。
13.解方程:(1);(2)
14.解方程:
(1)
(2)
15.解方程:
(1)+1=.
(2)-2=
16.解方程:
(1) (2)
17.解方程:
??
??+1
?
4
??
2
?1
=1.
18.解方程:﹣=1
19.解分式方程: -1=
20.解下列分式方程:
(1) (2).
21.解分式方程:=1.
22.解方程:+=1
23.解方程:.
24.阅读理解:
关于x的方程:x+=c+的解为x1=c,x2=;x﹣=c﹣(可变形为x+=c+)的解为x1=c,x2=;x+=c+的解为x1=c,x2= Zx+=c+的解为x1=c,x2=Z.
(1)归纳结论:根据上述方程与解的特征,得到关于x的方程x+=c+(m≠0)的解为 .
(2)应用结论:解关于y的方程y﹣a=﹣
参考答案
1.(1)无解;(2)x=6.
【解析】
(1)
去分母得,
去括号得,,
移项合并得,3x=3
解得,x=1,
经检验,x=1是增根,原方程无解;
(2)
去分母得,,
去括号得,
移项合并得,x=6,
经检验,x=6是原方程的解.
2..
【解析】
解:方程两边同时乘以,得
解这个方程,得.
经检验:是原方程的根,
∴原方程的解是:.
3.??=?2.
【解析】
4+
??
2
=??(???2),
2??=?4,
??=?2.
经检验:??=?2是原方程的解.
∴原方程的解为??=?2.
4.原方程无解.
【解析】
解:去分母得:,
解得,
经检验是增根,舍去
所以,原方程无解.
5..
【解析】
解:原方程即为:,
方程两边同时乘以,得,
解这个方程,得.
经检验:是原方程的解,所以原方程的解是.
6.(1);(2)
【解析】
解:(1)去分母得:3x-3=2x, 解得:x=3, 经检验x=3是分式方程的解; (2)去分母得:x-3+x-2=-3,
解得:x=1, 经检验x=1是分式方程的解;
7.(1)x= -(2)m>-6且m≠-4
【解析】
解:(1)?1=
两边都乘(x+2)(x?2),得
x(x+2)?(x+2)(x?2)=1,
解得x=?,
检验:当x=?时,(x+2)(x?2)=?≠0,
∴原分式方程的解为x=?;
(2)=3
去分母,得2x+m=3(x?2),
去括号,得2x+m=3x?6,
解得:x=m+6,
根据题意得:m+6?2≠0且m+6>0,
解得:m>?6且m≠?4.
故答案是:(1) x=?;(2)m>?6且m≠?4.
8.
【解析】
解:
方程两边同乘以得
去括号的
移项得
合并得
系数
检验:当时,
∴原分式方程的解为
9.x=1
【解析】
去分母得:x(x﹣2)﹣2=x2﹣4,
解得:x=1,
经检验x=1是分式方程的解.
10.(1)x=5是原方程的解;(2)原方程无解.
【解析】
(1)解:两边乘以最简公分母,得
,
即,
解得:x=5,
检验:把x=5代入最简公分母原 ,
因此x=5是原方程的解.
(2)解:方程两边同乘最简公分母得
x+2=4,
解得:x=2,
检验:把x=2代入最简公分母中,=(2+2)(2-2)=0,
故x=2是原方程的增根,所以原方程且无解.
11..
【解析】
解分式方程去分母转化成一元一次方程,分式方程一定要检验
12.当x=时,A与B的值相等
【解析】
整体分析:
由题意得分式方程,解这个分式,注意需要验根.
解:由A=B,得,
方程两边都乘以(x-2)(x+2),去分母得x(x+2)-x2+4=3,
解得x=.
经检验x=是原方程的解.
所以当x=时,A与B的值相等.
13.(1)无解;(2).
【解析】
解:(1)方程两边同时乘以,得,
解这个方程,得.
经检验是原方程的增根,所以原方程无解.
(2)方程两边同时乘以,得,
解这个方程,得.
经检验是原方程的根,所以原方程的解是.
14.(1);(2)无解
【解析】
(1)去分母得:3?x?1=x?4,
解得:x=3,
经检验x=3是分式方程的解;
(2)
去分母得:2x=x-2,
解得:x=-2,
经检验x=-2是分式方程增根,故原方程无解.
15.(1);(2)x=-7
【解析】
(1)+1=,
两边都乘以(x+1)(x-1),得
3(x+1)+ (x+1)(x-1)=x2,
解之得
,
检验:当时,(x+1)(x-1) ≠0,
∴是原方程的根;
(2)-2=,
两边都乘以 (x-3),得
1-2(x-3)=-3x,
解之得
x=-7,
检验:当x=-7时,x-3 ≠0,
∴x=-7是原方程的根.
16.(1)2;(2)无解
【解析】
解::(1)去分母得:7+3(x-1)=x, 去括号得:7+3x-3=x, 移项合并得:2x=-4, 解得:x=-2, 经检验x=-2是分式方程的解;
(2)去分母得:x+2=4, 移项合并得:x=2, 解得:x=2, 经检验x=2是增根,分式方程无解.
17.x=﹣3.
【解析】
首先去掉分母,观察可得最简公分母是
??
2
?1,方程两边乘最简公分母,可以把分式方程转化为整式方程求解,然后解一元一次方程,最后检验即可求解.
试题解析:方程两边同乘以
??
2
?1,得??(???1)?4=
??
2
?1,
解得??=?3.
经检验,??=?3是原方程的根.
∴原方程的解为??=?3.
18.x=﹣28
【解析】
解:去分母,得(x+4)2﹣6(x﹣4)=(x﹣4)(x+4)
去括号,得x2+8x+16﹣6x+24=x2﹣16
移项,合并同类项,得2x=﹣56
系数化为1,得x=﹣28
检验:当x=﹣28时,(x﹣4)(x+4)≠0,
所以原方程的解是x=﹣28.
19.7
【解析】
-1=
3-(x-3)=-1
3-x+3=-1
x=7
20.(1)x=3;(2)x=2
【解析】
解:(1)两边都乘以最简公分母x(x-1),得: 3(x-1)=2x, 去括号得:3x-3=2x, 解得: x=3, 经检验x=3是原分式方程的解;
(1)两边都乘以最简公分母(x+1)(x-1),得: 3(x-1)+(x+1)=6, 去括号得:3x-3+x+1=6, 解得: x=2, 经检验x=2是原分式方程的解.
故答案为(1)x=3;(2)x=2.
21.X=-1
【解析】
去分母得x(x+2)-2=(x+2)(x-2), 解得x=-1, 检验:当x=-1时,(x+2)(x-2) ≠0, 所以原方程的解为x=-1. 故答案为x=-1.
22.x = 1
【解析】
【详解】
方程两边乘(x-2)得:
3x - 4 = x-2,
解得:x = 1
检验:当x=1时,x-2≠0,
∴x=1是原方程的解.
23.x=1.
【解析】
方程两边都乘(2x-3),得
x-5=4(2x-3),
解得x=1.
检验:当x=1时,2x-3≠0.
∴原方程的根是x=1.
24.(1)x1=c,x2=;(2)y1=a,y2=.
【解析】
解:(1)仿照题意得:方程解为x1=c,x2=;
故答案为:x1=c,x2=;
(2)方程变形得:y﹣1+=a﹣1+,
∴y﹣1=a﹣1或y﹣1=,
解得:y1=a,y2=.
