人教版数学八年级下册17.2 勾股定理的逆定理同步练习(解析版)
文档属性
| 名称 | 人教版数学八年级下册17.2 勾股定理的逆定理同步练习(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 493.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 17:04:18 | ||
图片预览



文档简介
17.2 勾股定理的逆定理
1.下列命题的逆命题是真命题的是 ( )
A.对顶角相等 B.正方形的四个角都是直角
C.两直线平行,同位角相等 D.菱形的对角线互相垂直
2.下列定理有逆定理的是 ( )
A.直角都相等 B.同旁内角互补,两直线平行
C.同位角相等 D.全等三角形的对应角相等
3.下列各组数是三角形的三边长,不能组成直角三角形的一组数是 ( )
A.3,4,5 B.6,8,10
C.1.5,2,2.5 D.
4.若一个三角形的三边长之比为8:15:17,则它为________三角形.
5.如图17-2-1.以△ABC的三边为直径分别向三角形外侧作半圆,其中两个半圆的面积和等于另一个半圆的面积,则此三角形的形状为________.
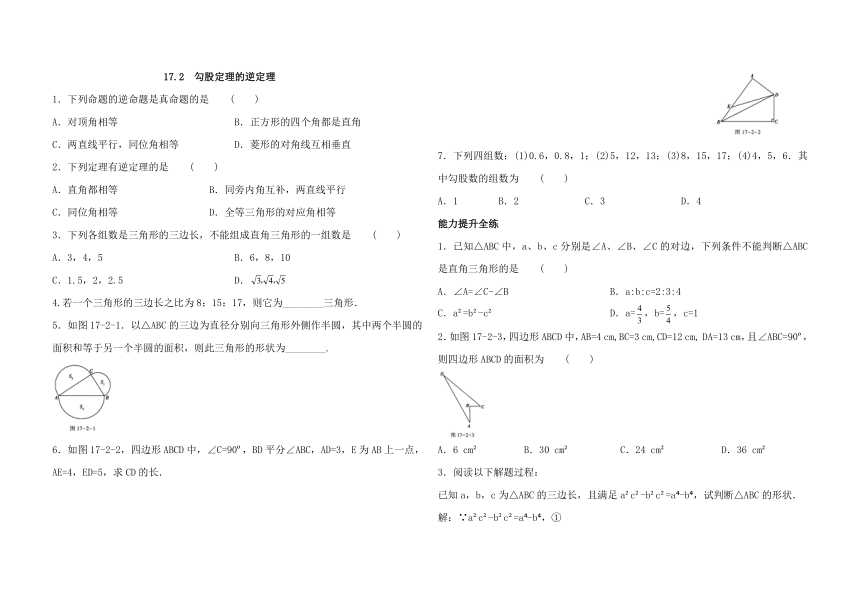
6.如图17-2-2,四边形ABCD中,∠C=90?,BD平分∠ABC,AD=3,E为AB上一点,AE=4,ED=5,求CD的长.
7.下列四组数:(1)0.6,0.8,1;(2)5,12,13;(3)8,15,17;(4)4,5,6.其中勾股数的组数为 ( )
A.1 B.2 C.3 D.4
能力提升全练
1.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是 ( )
A.∠A=∠C-∠B B.a:b:c=2:3:4
C.a?=b?-c? D.a=,b=,c=1
2.如图17-2-3,四边形ABCD中,AB=4 cm,BC=3 cm,CD=12 cm, DA=13 cm,且∠ABC=90?,则四边形ABCD的面积为 ( )
A.6 cm? B.30 cm? C.24 cm? D.36 cm?
3.阅读以下解题过程:
已知a,b,c为△ABC的三边长,且满足a?c?-b?c?=a?-b?,试判断△ABC的形状.
解:∵a?c?-b?c?=a?-b?,①
∴c?(a?-b?)=(a?-b?)(a?+b?),②
∴c?=a?+b?.③
∴△ABC为直角三角形,④
(1)上述解题过程从哪一步开始出现错误?请写出该步的代号__________;
(2)错误的原因是________________________________________________________;
(3)本题正确的结论是____________________________________________________.
三年模拟全练
一、选择题
1.F列四组线段中,可以构成直角三角形的是 ( )
A.1.5,2,2.5 B.4,5,6
C.2,3,4 D.1,,3
2.下列各组数中,是勾股数的为 ( )
A.1,1,2 B.1.5,2,2.5
C.7,24,25 D.6,12,13
3.甲、乙两艘客轮同时离开港口,航行的速度都是每分钟40 m,甲客轮用15分钟到达点A.乙客轮用20分钟到达点B,若A、B两点的直线距离为1000 m,甲客轮沿着北偏东30?的方向航行,则乙客轮的航行方向可能是 ( )
A.南偏东60? B.南偏西60? C.北偏西30? D.南偏西30?
二、填空题
4.三角形的三边长为a,b,c,且满足(a+b)?=c?+2ab,则这个三角形是_________.
三、解答题
5.如图17-2-4,每个小正方形的边长都为1.
(1)求四边形ABCD的面积与周长;
(2)∠DAB是直角吗?
五年中考模拟
一、选择题
1.下列长度的三条线段能组成直角三角形的是 ( )
A.3,4,5 B.2,3,4 C.4,6,7 D.5,11,12
2.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为 ( )
A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米
二、填空题
3.如图17-2-5,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上.则∠ACB的大小为_______.
核心素养全练
1.王老师在一次“探究性学习”课中设计了如下数表:
n 2 3 4 5 …
a 2?-1 3?-1 4?-1 5?-1 …
b 4 6 8 10 …
c 2?+1 3?+1 4?+1 5?+1 …
(1)请你分别观察a、b、c与n之间的关系,并用含自然数n(n>1)的代数式表示a、b、c;
(2)猜想:以a、b、c为边长的三角形是不是直角三角形,请证明你的猜想.
2.如图17-2-6,南北线MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时50分,我国反走私艇A发现正东方有一走私艇C以13海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇曰密切注意,反走私艇A和走私艇C的距离是13海里,A、B两艇的距离是5海里,反走私艇B和走私艇C的距离是12海里,若走私艇C的速度不变,最早会在什么时候进入我国领海?
3.阅读下面的材料,然后解答问题:
我们新定义一种三角形,两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形,
理解:
①根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?________(填“是”或“不是”);
②若某三角形的三边长分别为1、、2,则该三角形________(填“是”或“不是”)奇异三角形.
探究:
在Rt△ABC中,两边长分别是a、c,且a?=50,c?=100,则这个三角形是不是奇异三角形?请说明理由,
拓展:
在Rt△ABC中,∠C=90?,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a?:b?:c?.
17.2 勾股定理的逆定理
1.C“两直线平行,同位角相等”的逆命题是“同位角相等,两直线平行”,是平行线判定定理,所以逆命题是真命题.
2.B“直角都相等”的逆命题是“相等的角是直角”,选项A错误;“同旁内角互补,两直线平行”的逆命题是“两直线平行,同旁内角互补”,选项B正确;“同位角相等”的逆命题是“相等的角是同位角”,选项C错误;“全等三角形的对应角相等”的逆命题是“角对应相等的三角形是全等三角形”,选项D错误,故选B.
3.D ∵3?+4?=5?,∴此三角形是直角三角形,选项A不合题意;∵6?+8?=10?,∴此三角形是直角三角形,选项B不合题意;∵1.5?+2?=2.5?,∴此三角形是直角三角形,选项C不合题意;,∴此三角形不是直角三角形,选项D符合题意,故选D.
4.答案 直角
解析设三边长分别为8k,15k,17k( k>0),则(8k)?+(15k)?=289k?=(17k)?,由勾股定理的逆定理,可判断此三角形为直角三角形.
5.答案 直角三角形
解析 由题意得S?+S?=S?,即,∴BC?+AC?=AB?,
∴△ABC为直角三角形.
6.解析 ∵AD=3,AE=4,ED=5,
∴AD?+AE?=ED?.
∴∠A=90?,
∴DA⊥AB.
∵∠C=90?,
∴DC⊥BC.
∵BD平分∠ABC,
∴CD=AD=3.
7.B(1)中各数不全是正整数;(2)中5?+12?=13?;(3)中8?+15?=17?;(4)中4?+5?≠6?.故有2组勾股数.
1.B A.由条件可得∠A+∠B=∠C,且∠A+∠B+∠C=180?,可求得∠C=90?,故△ABC为直角三角形;B.不妨设a=2,b=3,c=4,此时a?+b?=13,而c?=16,即a?+b?≠c?,故△ABC不是直角三角形;C.由条件可得到a?+c?=b?,满足勾股定理的逆定理,故△ABC是直角三角形;D.由条件有a?+c?=,满足勾股定理的逆定理,故△ABC是直角三角形.故选B.
2.C 连接 AC, ∵∠ABC=90?,AB=4 cm,BC=3 cm,
∴AC=5 cm,∵CD=12 cm,DA=13 cm,AC?+CD?=5?+12?=169=13?=DA?,∴△ADC为直角三角形,
∴S四边形ABCD=S△ACD - S△ABC
=AC?CD-AB?BC
=×5×12-×4×3=30-6=24(cm?).
故四边形ABCD的面积为24 cm?.故选C.
3.答案 (1)③ (2)不能确定a?-b?是不是0 (3)△ABC是等腰三角形或直角三角形
解析 ∵c?(a?-b?)=(a?-b?)(a?+b?),∴(a?-b?)[c?-(a?+b?)]=0,∴a?-b?=0或c?-(a?+b?)=0,即a=b或a?+b?=c?,∴三角形为等腰三角形或直角三角形,故从第③步开始错误,其原因是不能确定a?-b?是不是0.
一、选择题
1.A根据勾股定理的逆定理判断,求出两短边的平方和与最长边的平方,判断是否相等即可.1.5?+2?=2.5?.即三角形是直角三角形,故此选项正确.故选A.
2.C A ∵1?+1?≠2?,∴不是勾股数,此选项错误;
B.1.5和2.5不是正整数,此选项错误;
C.∴7?+24?=25?,且7,24,25是正整数,∴是勾股数,此选项正确;
D.∵6?+12?≠13?,∴不是勾股数,此选项错误,
故选C.
3.A 如图,∵甲、乙两艘客轮同时离开港口,航行的速度都是每分钟40 m,甲客轮用15分钟到达点A,乙客轮用20分钟到达点B,∴甲客轮走了40×15=600(m),乙客轮走了40×20=800(m).
∵A、B两点间的直线距离为1000 m,又∵600?+800?=1000?,∴∠AOB=90?,
∵甲客轮沿着北偏东30?的方向航行,
∴乙客轮沿着南偏东60?的方向航行,故选A.
二、填空题
4.答案 直角三角形
解析化简(a+b)?=c?+2ab,得a?+b?=c?,所以该三角形是直角三角形.
三、解答题
5·解析(1)四边形ABCD的面积为25-1-×1×5-×1×4-×1×2-×2×4=14.5,
周长为AB+BC+CD+AD=.
(2)∠DAB是直角.理由如下:连接BD,
∴AB?+AD?=5+20=25,BD?=25.∴AB?+AD?=BD?.
∴△ABD是直角三角形,且∠DAB是直角.
一、选择题
1.A根据勾股定理的逆定理,能组成直角三角形的三边长必须满足两条较短边的平方和等于最长边的平方.∵3?+4?=5?,∴长为3,4,5的三条线段能组成直角三角形.故选A.
2.A 将里换算成以米为单位,则三角形沙田的三边长分别为2.5千米.6千米,6.5千米,因为2.5?+6?=6.5?,所以这个三角形为直角三角形,直角边长为2.5千米和6千米,所以S=×6×2.5=7.5(平方千米),故选A.
二、填空题
3.答案 90?
解析在网格中,由勾股定理得AC=,BC=.
AB=,
∴AC?+BC?=AB?.
∴由勾股定理的逆定理,知△ABC为直角三角形,且∠ACB=90?.
1.解析(1)由题表可以得出:
n=2时.a=2?-1,b=2×2,c=2?+1;
n=3时,a=3?-1,b=2×3,c=3?+1;
n=4时,a=4?-1,b=2×4,c=4?+1;
……
∴a=n?-1,b=2n,c=n?+1(n>1,且n为自然数).
(2)以a、b、c为边长的三角形是直角三角形,
证明:∵a?+b?=(n?-1)?+4n?=n?+2n?+1,
c?=(n?+1)?=n?+2n?+1,
∴a?+b2=c2.
∴以a、b、c为边长的三角形是直角三角形.
2.解析 设MN与AC相交于E,则∠BEC=90?,
∴AB?+BC?=5?+12?=13?=AC?.
∴△ABC为直角三角形,且∠ABC=90。.
∵MN⊥CE,∴走私艇C进入我国领海的最短距离是CE长,
由S△ABC=AB?BC=AC?BE,得BE=(海里),
由CE?+BE?=12?,得CE=(海里),
÷13=≈0.85(h)=51(min),
9时50分+51分=10时41分,
答:走私艇C最早在10时41分进入我国领海.
3.解析①设等边三角形的边长为a(a>0),
∵a?+a?=2a?.
∴等边三角形一定是奇异三角形.
②∵1?+()?=2×2?,∴该三角形是奇异三角形,
探究:当c为斜边时,b?=c?-a?=50,Rt△ABC不是奇异三角形:
当b为斜边时,b?=c?+a?=150,
∵50+150=2×100,∴ a?+b?=2c?,
∴Rt△ABC是奇异三角形.
拓展:Rt△ABC中,∠C=90?,
∴a?+b?=c?.
∴c>b>a,∴2c?>b?+a?,2a?<b?+c?,
∵Rt△ABC是奇异三角形,∴2b?=a?+c?,
∴2b2=a?+a?+b?,∴b?=2a?,∴c?=3a?,
∴a?:b?:c?=1:2:3.
1.下列命题的逆命题是真命题的是 ( )
A.对顶角相等 B.正方形的四个角都是直角
C.两直线平行,同位角相等 D.菱形的对角线互相垂直
2.下列定理有逆定理的是 ( )
A.直角都相等 B.同旁内角互补,两直线平行
C.同位角相等 D.全等三角形的对应角相等
3.下列各组数是三角形的三边长,不能组成直角三角形的一组数是 ( )
A.3,4,5 B.6,8,10
C.1.5,2,2.5 D.
4.若一个三角形的三边长之比为8:15:17,则它为________三角形.
5.如图17-2-1.以△ABC的三边为直径分别向三角形外侧作半圆,其中两个半圆的面积和等于另一个半圆的面积,则此三角形的形状为________.
6.如图17-2-2,四边形ABCD中,∠C=90?,BD平分∠ABC,AD=3,E为AB上一点,AE=4,ED=5,求CD的长.
7.下列四组数:(1)0.6,0.8,1;(2)5,12,13;(3)8,15,17;(4)4,5,6.其中勾股数的组数为 ( )
A.1 B.2 C.3 D.4
能力提升全练
1.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是 ( )
A.∠A=∠C-∠B B.a:b:c=2:3:4
C.a?=b?-c? D.a=,b=,c=1
2.如图17-2-3,四边形ABCD中,AB=4 cm,BC=3 cm,CD=12 cm, DA=13 cm,且∠ABC=90?,则四边形ABCD的面积为 ( )
A.6 cm? B.30 cm? C.24 cm? D.36 cm?
3.阅读以下解题过程:
已知a,b,c为△ABC的三边长,且满足a?c?-b?c?=a?-b?,试判断△ABC的形状.
解:∵a?c?-b?c?=a?-b?,①
∴c?(a?-b?)=(a?-b?)(a?+b?),②
∴c?=a?+b?.③
∴△ABC为直角三角形,④
(1)上述解题过程从哪一步开始出现错误?请写出该步的代号__________;
(2)错误的原因是________________________________________________________;
(3)本题正确的结论是____________________________________________________.
三年模拟全练
一、选择题
1.F列四组线段中,可以构成直角三角形的是 ( )
A.1.5,2,2.5 B.4,5,6
C.2,3,4 D.1,,3
2.下列各组数中,是勾股数的为 ( )
A.1,1,2 B.1.5,2,2.5
C.7,24,25 D.6,12,13
3.甲、乙两艘客轮同时离开港口,航行的速度都是每分钟40 m,甲客轮用15分钟到达点A.乙客轮用20分钟到达点B,若A、B两点的直线距离为1000 m,甲客轮沿着北偏东30?的方向航行,则乙客轮的航行方向可能是 ( )
A.南偏东60? B.南偏西60? C.北偏西30? D.南偏西30?
二、填空题
4.三角形的三边长为a,b,c,且满足(a+b)?=c?+2ab,则这个三角形是_________.
三、解答题
5.如图17-2-4,每个小正方形的边长都为1.
(1)求四边形ABCD的面积与周长;
(2)∠DAB是直角吗?
五年中考模拟
一、选择题
1.下列长度的三条线段能组成直角三角形的是 ( )
A.3,4,5 B.2,3,4 C.4,6,7 D.5,11,12
2.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为 ( )
A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米
二、填空题
3.如图17-2-5,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上.则∠ACB的大小为_______.
核心素养全练
1.王老师在一次“探究性学习”课中设计了如下数表:
n 2 3 4 5 …
a 2?-1 3?-1 4?-1 5?-1 …
b 4 6 8 10 …
c 2?+1 3?+1 4?+1 5?+1 …
(1)请你分别观察a、b、c与n之间的关系,并用含自然数n(n>1)的代数式表示a、b、c;
(2)猜想:以a、b、c为边长的三角形是不是直角三角形,请证明你的猜想.
2.如图17-2-6,南北线MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时50分,我国反走私艇A发现正东方有一走私艇C以13海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇曰密切注意,反走私艇A和走私艇C的距离是13海里,A、B两艇的距离是5海里,反走私艇B和走私艇C的距离是12海里,若走私艇C的速度不变,最早会在什么时候进入我国领海?
3.阅读下面的材料,然后解答问题:
我们新定义一种三角形,两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形,
理解:
①根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?________(填“是”或“不是”);
②若某三角形的三边长分别为1、、2,则该三角形________(填“是”或“不是”)奇异三角形.
探究:
在Rt△ABC中,两边长分别是a、c,且a?=50,c?=100,则这个三角形是不是奇异三角形?请说明理由,
拓展:
在Rt△ABC中,∠C=90?,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a?:b?:c?.
17.2 勾股定理的逆定理
1.C“两直线平行,同位角相等”的逆命题是“同位角相等,两直线平行”,是平行线判定定理,所以逆命题是真命题.
2.B“直角都相等”的逆命题是“相等的角是直角”,选项A错误;“同旁内角互补,两直线平行”的逆命题是“两直线平行,同旁内角互补”,选项B正确;“同位角相等”的逆命题是“相等的角是同位角”,选项C错误;“全等三角形的对应角相等”的逆命题是“角对应相等的三角形是全等三角形”,选项D错误,故选B.
3.D ∵3?+4?=5?,∴此三角形是直角三角形,选项A不合题意;∵6?+8?=10?,∴此三角形是直角三角形,选项B不合题意;∵1.5?+2?=2.5?,∴此三角形是直角三角形,选项C不合题意;,∴此三角形不是直角三角形,选项D符合题意,故选D.
4.答案 直角
解析设三边长分别为8k,15k,17k( k>0),则(8k)?+(15k)?=289k?=(17k)?,由勾股定理的逆定理,可判断此三角形为直角三角形.
5.答案 直角三角形
解析 由题意得S?+S?=S?,即,∴BC?+AC?=AB?,
∴△ABC为直角三角形.
6.解析 ∵AD=3,AE=4,ED=5,
∴AD?+AE?=ED?.
∴∠A=90?,
∴DA⊥AB.
∵∠C=90?,
∴DC⊥BC.
∵BD平分∠ABC,
∴CD=AD=3.
7.B(1)中各数不全是正整数;(2)中5?+12?=13?;(3)中8?+15?=17?;(4)中4?+5?≠6?.故有2组勾股数.
1.B A.由条件可得∠A+∠B=∠C,且∠A+∠B+∠C=180?,可求得∠C=90?,故△ABC为直角三角形;B.不妨设a=2,b=3,c=4,此时a?+b?=13,而c?=16,即a?+b?≠c?,故△ABC不是直角三角形;C.由条件可得到a?+c?=b?,满足勾股定理的逆定理,故△ABC是直角三角形;D.由条件有a?+c?=,满足勾股定理的逆定理,故△ABC是直角三角形.故选B.
2.C 连接 AC, ∵∠ABC=90?,AB=4 cm,BC=3 cm,
∴AC=5 cm,∵CD=12 cm,DA=13 cm,AC?+CD?=5?+12?=169=13?=DA?,∴△ADC为直角三角形,
∴S四边形ABCD=S△ACD - S△ABC
=AC?CD-AB?BC
=×5×12-×4×3=30-6=24(cm?).
故四边形ABCD的面积为24 cm?.故选C.
3.答案 (1)③ (2)不能确定a?-b?是不是0 (3)△ABC是等腰三角形或直角三角形
解析 ∵c?(a?-b?)=(a?-b?)(a?+b?),∴(a?-b?)[c?-(a?+b?)]=0,∴a?-b?=0或c?-(a?+b?)=0,即a=b或a?+b?=c?,∴三角形为等腰三角形或直角三角形,故从第③步开始错误,其原因是不能确定a?-b?是不是0.
一、选择题
1.A根据勾股定理的逆定理判断,求出两短边的平方和与最长边的平方,判断是否相等即可.1.5?+2?=2.5?.即三角形是直角三角形,故此选项正确.故选A.
2.C A ∵1?+1?≠2?,∴不是勾股数,此选项错误;
B.1.5和2.5不是正整数,此选项错误;
C.∴7?+24?=25?,且7,24,25是正整数,∴是勾股数,此选项正确;
D.∵6?+12?≠13?,∴不是勾股数,此选项错误,
故选C.
3.A 如图,∵甲、乙两艘客轮同时离开港口,航行的速度都是每分钟40 m,甲客轮用15分钟到达点A,乙客轮用20分钟到达点B,∴甲客轮走了40×15=600(m),乙客轮走了40×20=800(m).
∵A、B两点间的直线距离为1000 m,又∵600?+800?=1000?,∴∠AOB=90?,
∵甲客轮沿着北偏东30?的方向航行,
∴乙客轮沿着南偏东60?的方向航行,故选A.
二、填空题
4.答案 直角三角形
解析化简(a+b)?=c?+2ab,得a?+b?=c?,所以该三角形是直角三角形.
三、解答题
5·解析(1)四边形ABCD的面积为25-1-×1×5-×1×4-×1×2-×2×4=14.5,
周长为AB+BC+CD+AD=.
(2)∠DAB是直角.理由如下:连接BD,
∴AB?+AD?=5+20=25,BD?=25.∴AB?+AD?=BD?.
∴△ABD是直角三角形,且∠DAB是直角.
一、选择题
1.A根据勾股定理的逆定理,能组成直角三角形的三边长必须满足两条较短边的平方和等于最长边的平方.∵3?+4?=5?,∴长为3,4,5的三条线段能组成直角三角形.故选A.
2.A 将里换算成以米为单位,则三角形沙田的三边长分别为2.5千米.6千米,6.5千米,因为2.5?+6?=6.5?,所以这个三角形为直角三角形,直角边长为2.5千米和6千米,所以S=×6×2.5=7.5(平方千米),故选A.
二、填空题
3.答案 90?
解析在网格中,由勾股定理得AC=,BC=.
AB=,
∴AC?+BC?=AB?.
∴由勾股定理的逆定理,知△ABC为直角三角形,且∠ACB=90?.
1.解析(1)由题表可以得出:
n=2时.a=2?-1,b=2×2,c=2?+1;
n=3时,a=3?-1,b=2×3,c=3?+1;
n=4时,a=4?-1,b=2×4,c=4?+1;
……
∴a=n?-1,b=2n,c=n?+1(n>1,且n为自然数).
(2)以a、b、c为边长的三角形是直角三角形,
证明:∵a?+b?=(n?-1)?+4n?=n?+2n?+1,
c?=(n?+1)?=n?+2n?+1,
∴a?+b2=c2.
∴以a、b、c为边长的三角形是直角三角形.
2.解析 设MN与AC相交于E,则∠BEC=90?,
∴AB?+BC?=5?+12?=13?=AC?.
∴△ABC为直角三角形,且∠ABC=90。.
∵MN⊥CE,∴走私艇C进入我国领海的最短距离是CE长,
由S△ABC=AB?BC=AC?BE,得BE=(海里),
由CE?+BE?=12?,得CE=(海里),
÷13=≈0.85(h)=51(min),
9时50分+51分=10时41分,
答:走私艇C最早在10时41分进入我国领海.
3.解析①设等边三角形的边长为a(a>0),
∵a?+a?=2a?.
∴等边三角形一定是奇异三角形.
②∵1?+()?=2×2?,∴该三角形是奇异三角形,
探究:当c为斜边时,b?=c?-a?=50,Rt△ABC不是奇异三角形:
当b为斜边时,b?=c?+a?=150,
∵50+150=2×100,∴ a?+b?=2c?,
∴Rt△ABC是奇异三角形.
拓展:Rt△ABC中,∠C=90?,
∴a?+b?=c?.
∴c>b>a,∴2c?>b?+a?,2a?<b?+c?,
∵Rt△ABC是奇异三角形,∴2b?=a?+c?,
∴2b2=a?+a?+b?,∴b?=2a?,∴c?=3a?,
∴a?:b?:c?=1:2:3.
