人教版数学八年级下册19.3 课题学习 选择方案同步练习(解析版)
文档属性
| 名称 | 人教版数学八年级下册19.3 课题学习 选择方案同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 497.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 18:40:31 | ||
图片预览


文档简介
19.3 课题学习 选择方案
基础闯关全练
1.图19-3-1是甲、乙两家商店销售同一种产品的售价y(单位:元)与销售量x(单位:件)之间的函数图象,下列说法:①买2件时甲、乙两家商店的售价一样;②买1件时,买乙商店的合算;③买3件时,买甲商店的合算;④买1件时,乙商店的售价为3元.其中正确的是( )
A.①② B.①②③ C.②③ D.②③④
2.某电信局收取网费价格如下:163网费为每小时3元;169网费为每小时2元,但要收取每月基本费15元.设用163网每月上网总费用为y?元,用169网每月上网总费用为y?元,上网时间为x小时,如果一个网民每月上网19小时,他应选择_______.(填“163网”或“169网”)
3.“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以上信息,解答下列问题:
(1)设租车时间为x小时,租用甲公司的车所需费用为y?元,租用乙公司的车所需费用为y?元,如图19-3-2所示,分别求出y?,y?关于x的函数关系式;
(2)请你帮助小明计算选择哪个租车方案合算.
能力提升全练
江汉平原享有“中国小龙虾之乡”的美称.甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾,“龙虾节”期间,甲、乙两家商店都让利酬宾,实际付款金额,(单位:元)与原价x(单位:元)之间的函数关系如图19-3-3所示.
(1)直接写出,关于x的函数关系式;
(2)“龙虾节”期间,如何选择甲、乙两家商店购买小龙虾更省钱?
三年模拟全练
解答题
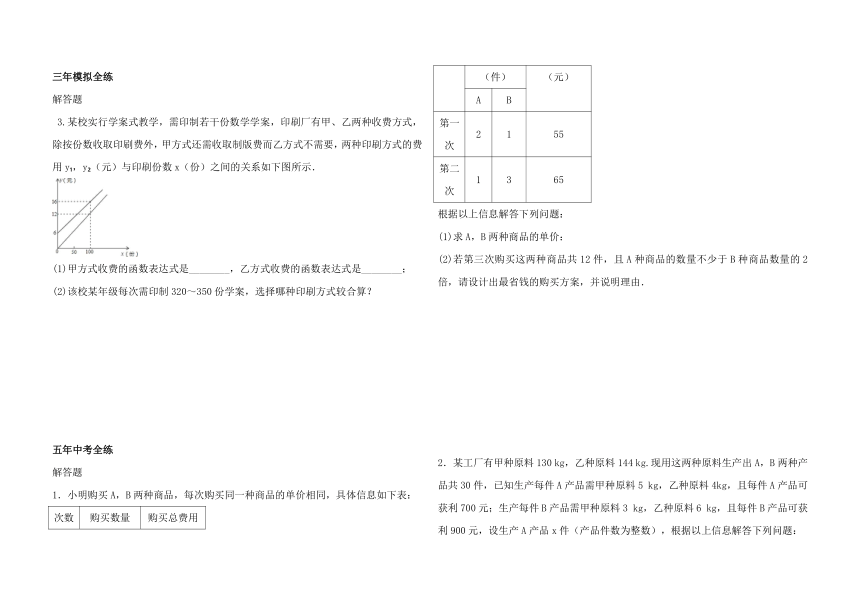
3.某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按份数收取印刷费外,甲方式还需收取制版费而乙方式不需要,两种印刷方式的费用y?,y?(元)与印刷份数x(份)之间的关系如下图所示.
(1)甲方式收费的函数表达式是________,乙方式收费的函数表达式是________;
(2)该校某年级每次需印制320~350份学案,选择哪种印刷方式较合算?
五年中考全练
解答题
1.小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数 购买数量(件) 购买总费用(元)
A B
第一次 2 1 55
第二次 1 3 65
根据以上信息解答下列问题:
(1)求A,B两种商品的单价:
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.
2.某工厂有甲种原料130 kg,乙种原料144 kg.现用这两种原料生产出A,B两种产品共30件,已知生产每件A产品需甲种原料5 kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3 kg,乙种原料6 kg,且每件B产品可获利900元,设生产A产品x件(产品件数为整数),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种?
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,找出(1)中利润最大的方案,并求出最大利润.
3.“绿水青山就是金山银山”.为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥,A,B两个果园分别需要110吨和70吨有机化肥.两个仓库到A.B两个果园的路程如下表所示:
路程(千米)
甲仓库 乙仓库
A果园 15 25
B果园 20 20
设甲仓库运往A果园x吨有机化肥,若汽车每吨每千米的运费为2元.
(1)根据题意,填写下表.
运量(吨) 运费(元)
甲仓库 乙仓库 甲仓库 乙仓库
A果园 x 110-x 2×15x 2×25(110-x)
B果园
设总运费为y元,求y关于x的函数表达式,并求当甲仓库运往A果园多少吨有机化肥时,总运费最省,最省的总运费是多少元?
核心素养全练
某景区内的环形路是边长为800米的正方形ABCD,如图19-3-5和图19-3-6所示,现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分.
探究设行驶时间为t分.
(1)当0≤t≤8时,分别写出1号车、2号车在左半环线离出口A的路程y?,y?(米)与t(分)的函数关系式,并求出当两车相距的路程是400米时t的值:
(2)t为何值时,1号车第三次恰好经过景点C?并直接写出这一段时间内它与2号车相遇过的次数.
发现 如图19-3-6,游客甲在BC上的一点K(不与点B,C重合)处候车,准备乘车到出口A.设CK=x米.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
比较哪种情况用时较多.(含候车时间)
决策 已知游客乙在DA上从D向出口A走去,步行的速度是50米/分.当行进到DA上一点P(不与点D,A重合)时,刚好与2号车迎面相遇.
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由;
(2)设PA=s(O<s<800)米,若他想尽快到达出口A,根据s的大小,在等候乘1号车还是步行这两种方式中,他该如何选择?
19.3课题学习 选择方案
1.B由题图知两图象的交点坐标为(2,4),即售出2件时,售价相同;在交点左侧,乙商店便宜;在交点右侧,甲商店便宜:买1件时,乙商店售价为2元,故选B.
2.答案169网
解析 由题意知y?=3x,y?=2x+15.当x=19时,y?=3×19=57,y?=2×19+15=53.
∵y?>y?,∴他应选择169网.
3.解析(1)由题意可设y?=k?x+80(k?≠0),把点(1,95)代入,可得95=k?+80,解得k?=15,∴y?=15x+80(x≥0);
设y?=k?x(k?≠O),把(1,30)代入,可得30=k?,即k?=30,
∴y?=30x(x≥0).
(2)当y?=y?时,即15x+80=30x,解得x=;
当y?>y?时,即15x+80>30x,解得x<;
当y?<y?时,即15x+80<30x,解得x>,
∴若租车时间为小时,选择方案一、方案二一样合算;若租车时间小于小时,选择方案二合算;若租车时间大于小时,选择方案一合算.
能力提升全练
解析(1)设=kx(k≠0),把(2000,1600)代入,得2000k=1600,解得k=0.8,所以=0.8x;
当O≤x≤2000时,设=ax(a≠0),把(2000,2000)代入,得2000a=2000,解得a=1.
所以=x;
当x≥2000时,设=mx+n(m≠0),把(2000,2000),(4000,3400)代入,
得 所以
(2)当0≤x<2000时,0.8x<x,即<,故到甲商店购买更省钱.
当x≥2000时,若到甲商店购买更省钱,则0.8x<0.7x+600,解得x<6000;
若到乙商店购买更省钱,则0.8x>0.7x+600,解得x>6000;
若到甲、乙两商店购买实际付款金额一样,则0.8x=0.7x+600.解得x=6000.
故当购买金额原价小于6000元时,到甲商店购买更省钱;
当购买金额原价大于6000元时,到乙商店购买更省钱;
当购买金额原价等于6000元时,到甲、乙两商店购买实际付款金额一样.
三年模拟全练
解答题
解析(1)y?=0.1x+6;y?=0.12x.
设甲种收费方式的函数表达式为y?=k?x+b(k?≠0),乙种收费方式的函数表达式为y?=k?x(k?≠0),
把(0,6),(100,16)代入y?=k?x+b,得
解得∴y?=0.1x+6(x≥0且x为整数),
把(100,12)代入y?=k?x,解得k?=0.12,
∴y?=0.12x(x≥0且x为整数).
(2)由题意,得
当y?>y?时,有0.1x+6>0.12x,解得x<300;
当y?=y?时,有0.1x+6=0.12x,解得x=300;
当y?<y?时,有0.1x+6<0.12x,解得x>300,
∴印制320~350份学案时,选择甲方式收费较合算.
五年中考全练
解答题
1.解析(1)设A,B两种商品的单价分别为x元/件,y元/件,根据题意,得解得
(2)设第三次购买A种商品m件,购买商品的总费用为W元,则购买B种商品(12-m)件.
W=20m+15(12-m)=5m+180.
又由题意可知m≥2(12-m),∴m≥8.
∵W=5m+180中,k=5>0,∴W随m的增大而增大,
∴当m=8时,W有最小值,此时12-m=4.
∴最省钱的购买方案是购买A种商品8件,B种商品4件.
2.解析 (1)根据题意得
解得18≤x≤20.
∵x是整数,∴x=18或19或20.
∴共有三种方案:
方案一:生产A产品18件,B产品12件;
方案二:生产A产品19件,B产品11件;
方案三:生产A产品20件,B产品10件.
(2)根据题意得y=700x+900(30-x)=-200x+27000,
∵-200<0,∴y随x的增大而减小,
又∵18≤x≤20.
∴当x=18时,y有最大值,y最大值=-200×18+27000=23400.
∴利润最大的方案是方案一:生产A产品18件,B产品12件,最大利润为23400元.
3.解析(1)
运量(吨) 运费(元)
甲仓库 乙仓库 甲仓库 乙仓库
A果园 x 110-x 2×15x 2×25(110-x)
B果园 80-x x-10 2×20(80-x) 2×20(x-10)
(2)y=2×15x+2×25(110-x)+2×20(80-x)+2×20(x-10),
即y=-20x+8300.又∴10≤x≤80.
在一次函数y=-20x+8300中,∵-20<0,且10≤x≤80,
∴y随x的增大而减小,
∴当x=80时,y有最小值,y最小值=-20×80+8300=6700.
故当甲仓库运往A果园80吨有机化肥时,总运费最省,为6700元.
核心素养全练
解析 探究(1)y?=200t,y?=-200t+1600.
相遇前相距400米时,y?-y?=400,
即-200t+1600-200t=400.
解得t=3.
相遇后相距400米时,y?-y?=400,
即200t-(-200t+1 600)=400.
解得t=5.
故当t=3或5时,两车相距的路程是400米.
(2)当1号车第三次恰好经过景点C时,有200t=800×2+800×4×2.解得t=40.
易知两车在点B、点D处相遇,故这一段时间内它与2号车相遇过5次.
发现 情况一用时为;
情况二用时为.
∵x>0,∴<16<.∴情况二用时较多.
决策(1)由题意知,此时1号车正行驶在CD边上,乘1号车到达点A的路程小于2个边长的长度,而乘2号车的路程却大于3个边长的长度,所以乘1号车用时比乘2号车用时少(两车速度相同).
(2)若步行比等候乘1号车用时少,则,解得s<320.
∴当0<s<320时,选择步行;
同理可得:
当320<s<800时,选择等候乘1号车;
当s=320时,选择步行或等候乘1号车用时一样.
基础闯关全练
1.图19-3-1是甲、乙两家商店销售同一种产品的售价y(单位:元)与销售量x(单位:件)之间的函数图象,下列说法:①买2件时甲、乙两家商店的售价一样;②买1件时,买乙商店的合算;③买3件时,买甲商店的合算;④买1件时,乙商店的售价为3元.其中正确的是( )
A.①② B.①②③ C.②③ D.②③④
2.某电信局收取网费价格如下:163网费为每小时3元;169网费为每小时2元,但要收取每月基本费15元.设用163网每月上网总费用为y?元,用169网每月上网总费用为y?元,上网时间为x小时,如果一个网民每月上网19小时,他应选择_______.(填“163网”或“169网”)
3.“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以上信息,解答下列问题:
(1)设租车时间为x小时,租用甲公司的车所需费用为y?元,租用乙公司的车所需费用为y?元,如图19-3-2所示,分别求出y?,y?关于x的函数关系式;
(2)请你帮助小明计算选择哪个租车方案合算.
能力提升全练
江汉平原享有“中国小龙虾之乡”的美称.甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾,“龙虾节”期间,甲、乙两家商店都让利酬宾,实际付款金额,(单位:元)与原价x(单位:元)之间的函数关系如图19-3-3所示.
(1)直接写出,关于x的函数关系式;
(2)“龙虾节”期间,如何选择甲、乙两家商店购买小龙虾更省钱?
三年模拟全练
解答题
3.某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按份数收取印刷费外,甲方式还需收取制版费而乙方式不需要,两种印刷方式的费用y?,y?(元)与印刷份数x(份)之间的关系如下图所示.
(1)甲方式收费的函数表达式是________,乙方式收费的函数表达式是________;
(2)该校某年级每次需印制320~350份学案,选择哪种印刷方式较合算?
五年中考全练
解答题
1.小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数 购买数量(件) 购买总费用(元)
A B
第一次 2 1 55
第二次 1 3 65
根据以上信息解答下列问题:
(1)求A,B两种商品的单价:
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.
2.某工厂有甲种原料130 kg,乙种原料144 kg.现用这两种原料生产出A,B两种产品共30件,已知生产每件A产品需甲种原料5 kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3 kg,乙种原料6 kg,且每件B产品可获利900元,设生产A产品x件(产品件数为整数),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种?
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,找出(1)中利润最大的方案,并求出最大利润.
3.“绿水青山就是金山银山”.为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥,A,B两个果园分别需要110吨和70吨有机化肥.两个仓库到A.B两个果园的路程如下表所示:
路程(千米)
甲仓库 乙仓库
A果园 15 25
B果园 20 20
设甲仓库运往A果园x吨有机化肥,若汽车每吨每千米的运费为2元.
(1)根据题意,填写下表.
运量(吨) 运费(元)
甲仓库 乙仓库 甲仓库 乙仓库
A果园 x 110-x 2×15x 2×25(110-x)
B果园
设总运费为y元,求y关于x的函数表达式,并求当甲仓库运往A果园多少吨有机化肥时,总运费最省,最省的总运费是多少元?
核心素养全练
某景区内的环形路是边长为800米的正方形ABCD,如图19-3-5和图19-3-6所示,现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分.
探究设行驶时间为t分.
(1)当0≤t≤8时,分别写出1号车、2号车在左半环线离出口A的路程y?,y?(米)与t(分)的函数关系式,并求出当两车相距的路程是400米时t的值:
(2)t为何值时,1号车第三次恰好经过景点C?并直接写出这一段时间内它与2号车相遇过的次数.
发现 如图19-3-6,游客甲在BC上的一点K(不与点B,C重合)处候车,准备乘车到出口A.设CK=x米.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
比较哪种情况用时较多.(含候车时间)
决策 已知游客乙在DA上从D向出口A走去,步行的速度是50米/分.当行进到DA上一点P(不与点D,A重合)时,刚好与2号车迎面相遇.
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由;
(2)设PA=s(O<s<800)米,若他想尽快到达出口A,根据s的大小,在等候乘1号车还是步行这两种方式中,他该如何选择?
19.3课题学习 选择方案
1.B由题图知两图象的交点坐标为(2,4),即售出2件时,售价相同;在交点左侧,乙商店便宜;在交点右侧,甲商店便宜:买1件时,乙商店售价为2元,故选B.
2.答案169网
解析 由题意知y?=3x,y?=2x+15.当x=19时,y?=3×19=57,y?=2×19+15=53.
∵y?>y?,∴他应选择169网.
3.解析(1)由题意可设y?=k?x+80(k?≠0),把点(1,95)代入,可得95=k?+80,解得k?=15,∴y?=15x+80(x≥0);
设y?=k?x(k?≠O),把(1,30)代入,可得30=k?,即k?=30,
∴y?=30x(x≥0).
(2)当y?=y?时,即15x+80=30x,解得x=;
当y?>y?时,即15x+80>30x,解得x<;
当y?<y?时,即15x+80<30x,解得x>,
∴若租车时间为小时,选择方案一、方案二一样合算;若租车时间小于小时,选择方案二合算;若租车时间大于小时,选择方案一合算.
能力提升全练
解析(1)设=kx(k≠0),把(2000,1600)代入,得2000k=1600,解得k=0.8,所以=0.8x;
当O≤x≤2000时,设=ax(a≠0),把(2000,2000)代入,得2000a=2000,解得a=1.
所以=x;
当x≥2000时,设=mx+n(m≠0),把(2000,2000),(4000,3400)代入,
得 所以
(2)当0≤x<2000时,0.8x<x,即<,故到甲商店购买更省钱.
当x≥2000时,若到甲商店购买更省钱,则0.8x<0.7x+600,解得x<6000;
若到乙商店购买更省钱,则0.8x>0.7x+600,解得x>6000;
若到甲、乙两商店购买实际付款金额一样,则0.8x=0.7x+600.解得x=6000.
故当购买金额原价小于6000元时,到甲商店购买更省钱;
当购买金额原价大于6000元时,到乙商店购买更省钱;
当购买金额原价等于6000元时,到甲、乙两商店购买实际付款金额一样.
三年模拟全练
解答题
解析(1)y?=0.1x+6;y?=0.12x.
设甲种收费方式的函数表达式为y?=k?x+b(k?≠0),乙种收费方式的函数表达式为y?=k?x(k?≠0),
把(0,6),(100,16)代入y?=k?x+b,得
解得∴y?=0.1x+6(x≥0且x为整数),
把(100,12)代入y?=k?x,解得k?=0.12,
∴y?=0.12x(x≥0且x为整数).
(2)由题意,得
当y?>y?时,有0.1x+6>0.12x,解得x<300;
当y?=y?时,有0.1x+6=0.12x,解得x=300;
当y?<y?时,有0.1x+6<0.12x,解得x>300,
∴印制320~350份学案时,选择甲方式收费较合算.
五年中考全练
解答题
1.解析(1)设A,B两种商品的单价分别为x元/件,y元/件,根据题意,得解得
(2)设第三次购买A种商品m件,购买商品的总费用为W元,则购买B种商品(12-m)件.
W=20m+15(12-m)=5m+180.
又由题意可知m≥2(12-m),∴m≥8.
∵W=5m+180中,k=5>0,∴W随m的增大而增大,
∴当m=8时,W有最小值,此时12-m=4.
∴最省钱的购买方案是购买A种商品8件,B种商品4件.
2.解析 (1)根据题意得
解得18≤x≤20.
∵x是整数,∴x=18或19或20.
∴共有三种方案:
方案一:生产A产品18件,B产品12件;
方案二:生产A产品19件,B产品11件;
方案三:生产A产品20件,B产品10件.
(2)根据题意得y=700x+900(30-x)=-200x+27000,
∵-200<0,∴y随x的增大而减小,
又∵18≤x≤20.
∴当x=18时,y有最大值,y最大值=-200×18+27000=23400.
∴利润最大的方案是方案一:生产A产品18件,B产品12件,最大利润为23400元.
3.解析(1)
运量(吨) 运费(元)
甲仓库 乙仓库 甲仓库 乙仓库
A果园 x 110-x 2×15x 2×25(110-x)
B果园 80-x x-10 2×20(80-x) 2×20(x-10)
(2)y=2×15x+2×25(110-x)+2×20(80-x)+2×20(x-10),
即y=-20x+8300.又∴10≤x≤80.
在一次函数y=-20x+8300中,∵-20<0,且10≤x≤80,
∴y随x的增大而减小,
∴当x=80时,y有最小值,y最小值=-20×80+8300=6700.
故当甲仓库运往A果园80吨有机化肥时,总运费最省,为6700元.
核心素养全练
解析 探究(1)y?=200t,y?=-200t+1600.
相遇前相距400米时,y?-y?=400,
即-200t+1600-200t=400.
解得t=3.
相遇后相距400米时,y?-y?=400,
即200t-(-200t+1 600)=400.
解得t=5.
故当t=3或5时,两车相距的路程是400米.
(2)当1号车第三次恰好经过景点C时,有200t=800×2+800×4×2.解得t=40.
易知两车在点B、点D处相遇,故这一段时间内它与2号车相遇过5次.
发现 情况一用时为;
情况二用时为.
∵x>0,∴<16<.∴情况二用时较多.
决策(1)由题意知,此时1号车正行驶在CD边上,乘1号车到达点A的路程小于2个边长的长度,而乘2号车的路程却大于3个边长的长度,所以乘1号车用时比乘2号车用时少(两车速度相同).
(2)若步行比等候乘1号车用时少,则,解得s<320.
∴当0<s<320时,选择步行;
同理可得:
当320<s<800时,选择等候乘1号车;
当s=320时,选择步行或等候乘1号车用时一样.
