湘教版数学九年级上册第一章反比例函数单元测试题(含答案)
文档属性
| 名称 | 湘教版数学九年级上册第一章反比例函数单元测试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 297.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-05 09:10:05 | ||
图片预览

文档简介
第一章反比例函数单元测试题
姓名:__________ 班级:__________考号:__________
一、单选题(共10题;共30分)
1.下列四个点,在反比例函数y=图象上的是(??? )
A.?(1,-6) ??????????????????????????????????B.?(2,4)??????????????????????????????????C.?(3,-2)??????????????????????????????????D.?(-6,-1)
2.对于反比例函数y=﹣, 下列说法正确的是( )
A.?图象经过点(1,1)??????????????????????????????????????????B.?图象位于第一、三象限
C.?图象是中心对称图形???????????????????????????????????????????D.?当x<0时,y随x的增大而减小
3.如果点A(-1, )、B(1, )、C(2, )是反比例函数 图象上的三个点,则下列结论正确的是( )
A.?> > ???????????B.?> > ???????????C.?> > ???????????D.?> >
4.若y关于x的反比例函数y=经过点(3,-7),则它不经过的点是(???)
A.?(-3,7) B.?(-7,3) C.?(,-9) D.?(3,-7)
5.双曲线y=的图象经过第二、四象限,则k的取值范围是(?????? )
A.?k>???????????????????????????????????B.?k6.在xy+2=0中,y是x的( ).
A.?一次函数??????????B.?反比例函数??????????C.?正比例函数??????????D.?即不是正比例函数,也不是反比例函数
7.在的三个顶点中,可能在反比例函数的图象上的点是(????)。
A.?点A????????????????????????B.?点B????????????????????C.?点C??????????????????D.?三个点都在
8.如图,反比例函数y1=和正比例函数y2=k2x的图象交于A(-1,-3)、
B(1,3)两点,若>k2x,则x的取值范围是( )
A.?-1<x<0 B.?-1<x<1 C.?x<-1或0<x<1 D.?-1<x<0或x>1
9.如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,
将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数的图象恰好
经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
A.?3???????????????????????B.?4???????????????????????C.?6??????????????????????D.?8
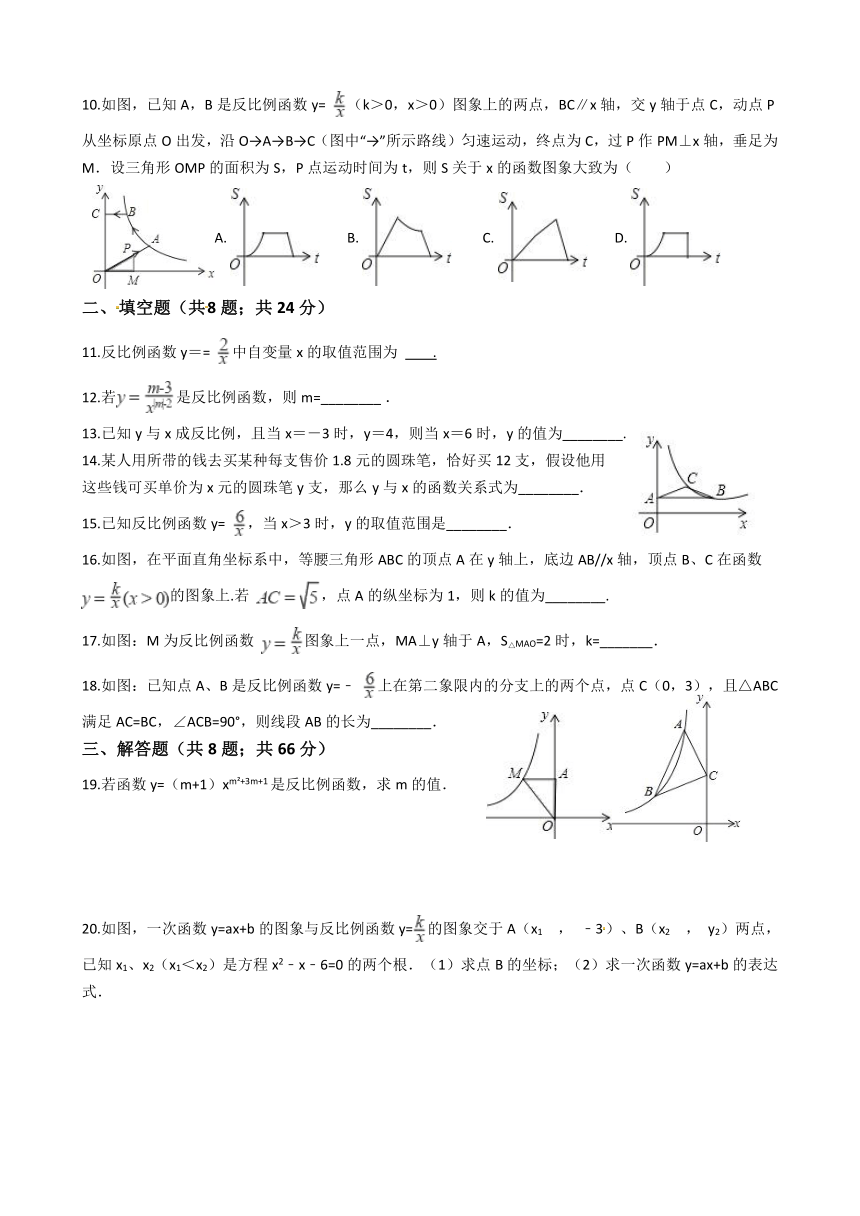
10.如图,已知A,B是反比例函数y= (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
A.?????????B.??????????C.?????????D.?
二、填空题(共8题;共24分)
11.反比例函数y== 中自变量x的取值范围为 ????????.
12.若是反比例函数,则m=________?.
13.已知y与x成反比例,且当x=-3时,y=4,则当x=6时,y的值为________.
14.某人用所带的钱去买某种每支售价1.8元的圆珠笔,恰好买12支,假设他用
这些钱可买单价为x元的圆珠笔y支,那么y与x的函数关系式为________.
15.已知反比例函数y= ,当x>3时,y的取值范围是________.
16.如图,在平面直角坐标系中,等腰三角形ABC的顶点A在y轴上,底边AB//x轴,顶点B、C在函数 的图象上.若 ,点A的纵坐标为1,则k的值为________.
17.如图:M为反比例函数 图象上一点,MA⊥y轴于A,S△MAO=2时,k=_______.
18.如图:已知点A、B是反比例函数y=﹣ 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为________.
三、解答题(共8题;共66分)
19.若函数y=(m+1)xm?+3m+1是反比例函数,求m的值.
20.如图,一次函数y=ax+b的图象与反比例函数y=的图象交于A(x1 , ﹣3)、B(x2 , y2)两点,已知x1、x2(x1<x2)是方程x2﹣x﹣6=0的两个根.(1)求点B的坐标;(2)求一次函数y=ax+b的表达式.
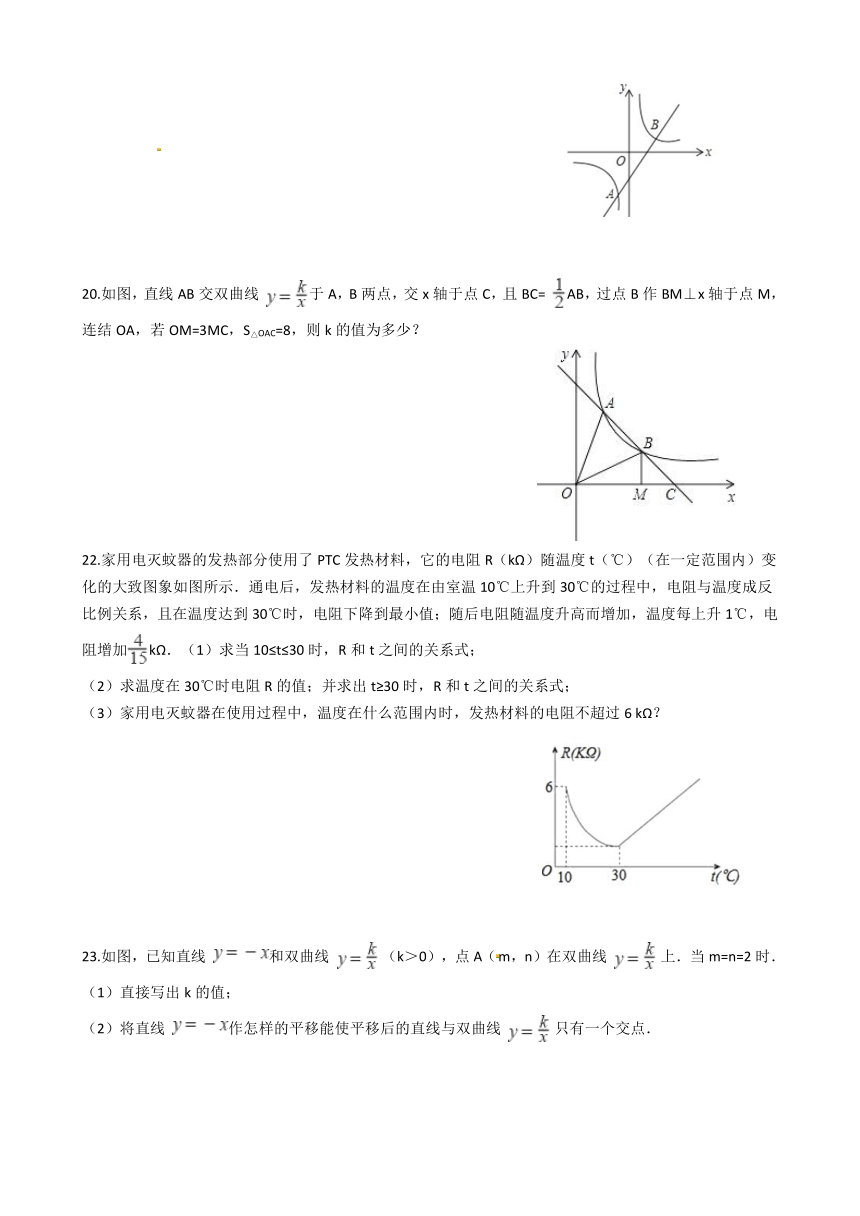
20.如图,直线AB交双曲线 于A,B两点,交x轴于点C,且BC= AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
22.家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反比例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻随温度升高而增加,温度每上升1℃,电阻增加kΩ.(1)求当10≤t≤30时,R和t之间的关系式;
(2)求温度在30℃时电阻R的值;并求出t≥30时,R和t之间的关系式;
(3)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过6 kΩ?
?
23.如图,已知直线 和双曲线 ?(k>0),点A(m,n)在双曲线 ?上.当m=n=2时.
(1)直接写出k的值;
(2)将直线 作怎样的平移能使平移后的直线与双曲线 ?只有一个交点.
24.如图,已知反比例函数y= 与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4).
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△AOB的面积.
25.已知反比例函数y= (k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1 , y1)、B(x2 , y2),当y1>y2时,试比较x1与x2的大小.
26.如图,一次函数y=kx+b的图象l与坐标轴分别交于点E,F,与双曲线y=﹣
(x<0)交于点P(﹣1,n),且F是PE的中点.(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),
①当a为何值时,△ABP是以点P为直角顶点的直角三角形?
②当a为何值时,PA=PB.
答案
一、单选题
1.D 2.C 3.A 4.C 5.B 6.B 7.B 8.C 9.C 10.A
二、填空题
11.x≠0 12.-3 13.-2 14.y= 15.0<y<2 16.4 17.﹣4 18.2
三、解答题
19.解:由函数y=(m+3)x?m?+3m+1为反比例函数可知m2+3m+1=-1,且m+1≠0
解得m=-1(舍去),m=-2,m的值是-2
20.解:(1)∵x1、x2是方程x2﹣x﹣6=0的两个根,∴(x﹣3)(x+2)=0,
解得x1=3,x2=﹣2;∴点A坐标为(﹣2,﹣3),
代入y=得k=6.∴反比例函数的解析式y=,
把x2=3代入反比例函数的解析式得y2=2,∴点B坐标为(3,2);
(2)把点A、B代入一次函数的解析式,得,解得,
∴一次函数的表达式为y=x﹣1.
21.解:设B(a,b), ∵点B在函数y= 上,∴ab=k,且OM=a,BM=b,
∵OM=3MC,∴MC= a,∴S△BOM= ab= k,S△BMC= × ab= ab= k,
∴S△BOC=S△BOM+S△BMC= k+ k= k,
∵BC= AB,不妨设点O到AC的距离为h,则 = = = ,
∴S△AOB=2S△BOC= k,∴S△AOC=S△AOB+S△BOC= k+ k=2k,
∵S△AOC=8.∴2k=8,∴k=4
22.解:(1)∵温度在由室温10℃上升到30℃的过程中,电阻与温度成反比例关系,
∴可设R和t之间的关系式为R=,将(10,6)代入上式中得:6=,k=60.
故当10≤t≤30时,R=;
(2)将t=30℃代入上式中得:R=,R=2.∴温度在30℃时,电阻R=2(kΩ).
∵在温度达到30℃时,电阻下降到最小值;随后电阻随温度升高而增加,温度每上升1℃,电阻增加kΩ,
∴当t≥30时,R=2+(t﹣30)=t﹣6;
(3)把R=6(kΩ),代入R=t﹣6得,t=45(℃),
所以,温度在10℃~45℃时,电阻不超过6kΩ.
23.(1)解:当m=n=2时,A(2,2),把点A(2,2)代入双曲线 (k>0)得:k=2×2=4;
(2)解:设平移后的直线解析式为y=﹣x+b1 , 由 ?可得, ,整理可得:x2﹣b1x+4=0,当△= ,即b1=±4时,方程x2﹣b1x+4=0有两个相等的实数根,此时直线y=﹣x+b1与双曲线只有一个交点,∴只要将直线y=﹣x向上或向下平移4个单位长度,所得到的直线与双曲线只有一个交点
24.(1)解:∵已知反比例函数y= 与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4),
∴﹣k+4=k,解得k=2,故反比例函数的解析式为y= ,
又知A(1,2)在一次函数y=x+b的图象上,故2=1+b,解得b=1,
故一次函数的解析式为y=x+1
(2)解:由题意得: ,解得x=﹣2或1,∴B(﹣2,﹣1),
令y=0,得x+1=0,解得x=﹣1,∴C(﹣1,0),∴S△A0B=S△A0C+S△C0B= ×1×2+ ×1×1=1+ = .
25.解:(Ⅰ)由题意,设点P的坐标为(m,2)
∵点P在正比例函数y=x的图象上,∴2=m,即m=2.∴点P的坐标为(2,2).
∵点P在反比例函数y= 的图象上,∴2= ,解得k=5.
(Ⅱ)∵在反比例函数y= 图象的每一支上,y随x的增大而减小,
∴k﹣1>0,解得k>1.
(Ⅲ)∵反比例函数y= 图象的一支位于第二象限,
∴在该函数图象的每一支上,y随x的增大而增大.
∵点A(x1 , y1)与点B(x2 , y2)在该函数的第二象限的图象上,且y1>y2 ,
∴x1>x2
26.(1)解:∵点P(﹣1,n)在反比例函数y=﹣ 图象上,∴n=4,∴P(﹣1,4),
∵F是PE的中点,∴F(0,2),∴ ,∴ ,∴y=﹣2x+2
(2)解:①∵△ABP是以点P为直角顶点的直角三角形,∴∠APB=90°=∠EOF,
∵直线AB∥y轴,∴∠BAP=∠OFE,∴△APB∽△FOE,∴ =
当x=a时,y=﹣2a+2,∴A(a,﹣2a+2),
∵P(﹣1,4),∴AP= = = |a+1|
当x=a时,y=﹣ ,∴B(a,﹣ ),∴AB=|﹣2a+2+ ,
∵直线EF的解析式为y=﹣2x+2,∴E(1,0),F(0,2),∴OF=2,EF= ,∴ ,
∴a= (舍)或a=﹣1(舍)或a=﹣8,
即:a=﹣8时,△ABP是以点P为直角顶点的直角三角形;
②如图,
过P作PD⊥AB,垂足为点D,
∵P(﹣1,4),∴D点的纵坐标为4,
∵PA=PB,∴点D为AB的中点,
由题意知,A点的纵坐标为﹣2a+2,B点的纵坐标为 ,
∴ ,解得a1=﹣2,a2=﹣1(舍去).∴当a=﹣2时,PA=PB
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
