山东省淄博市博山区2019-2020学年六年级(上)期中数学试卷(五四学制) (解析版)
文档属性
| 名称 | 山东省淄博市博山区2019-2020学年六年级(上)期中数学试卷(五四学制) (解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 169.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 00:00:00 | ||
图片预览





文档简介
2019-2020学年六年级(上)期中数学试卷
一.选择题(共12小题)
1.比﹣2小1的数是( )
A.﹣3 B.﹣1 C.1 D.3
2.国产科幻电影《流浪地球》上映17日,票房收入突破40亿元人民币,将40亿用科学记数法表示为( )
A.40×108 B.4×109 C.4×1010 D.0.4×1010
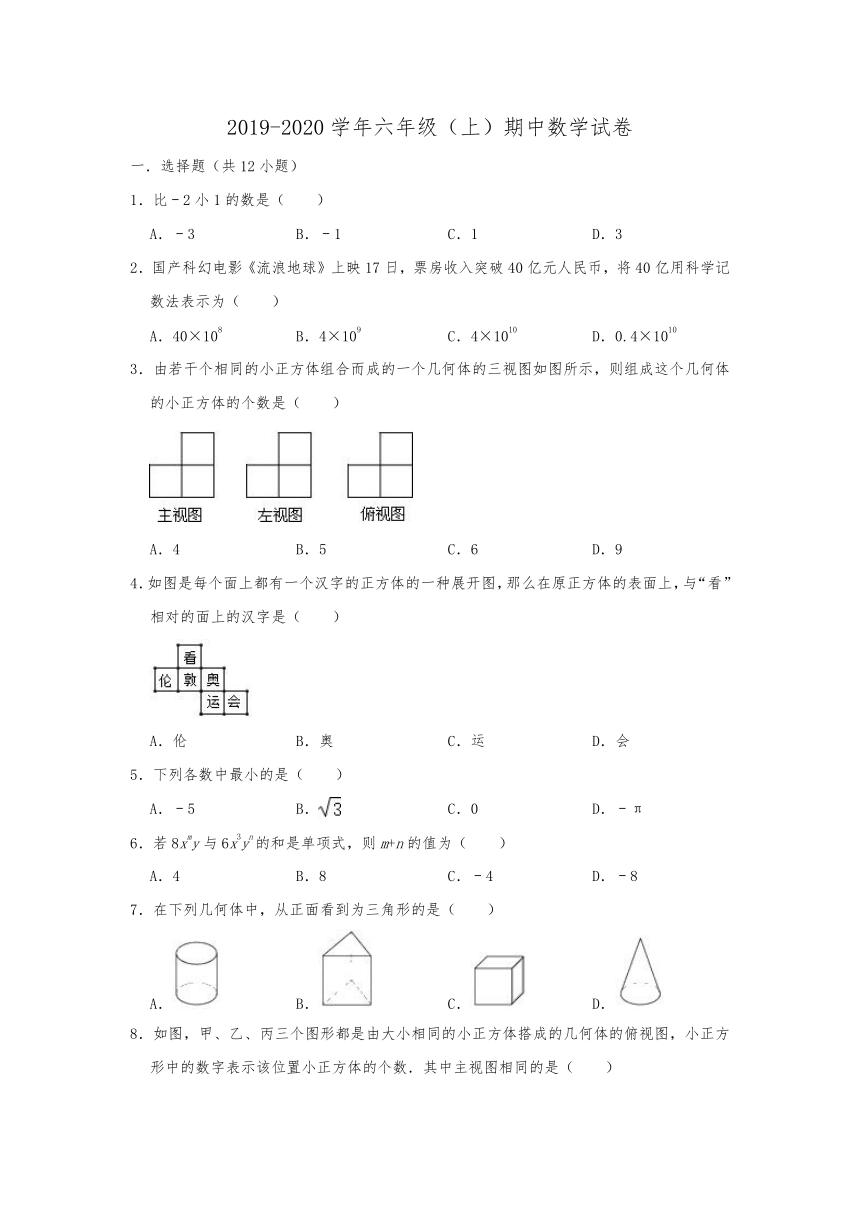
3.由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.9
4.如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与“看”相对的面上的汉字是( )
A.伦 B.奥 C.运 D.会
5.下列各数中最小的是( )
A.﹣5 B. C.0 D.﹣π
6.若8xmy与6x3yn的和是单项式,则m+n的值为( )
A.4 B.8 C.﹣4 D.﹣8
7.在下列几何体中,从正面看到为三角形的是( )
A. B. C. D.
8.如图,甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是( )
A.仅有甲和乙相同 B.仅有甲和丙相同
C.仅有乙和丙相同 D.甲、乙、丙都相同
9.|﹣2019|=( )
A.2019 B.﹣2019 C. D.﹣
10.计算下列各式,值最小的是( )
A.2×0+1﹣9 B.2+0×1﹣9 C.2+0﹣1×9 D.2+0+1﹣9
11.用计算器计算230,按键顺序正确的是( )
A.
B.
C.
D.
12.如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )
A.点A的左边 B.点A与点B之间
C.点B与点C之间 D.点C的右边
二.填空题(共8小题)
13.子弹从枪膛中射出去的轨迹、汽车的雨刷把玻璃上的雨水刷干净,可分别看作是 、 的实际应用.
14.某地一周前四天每天的最高气温与最低气温如表,则这四天中温差最大的是 .
星期 一 二 三 四
最高气温 10°C 12°C 11°C 9°C
最低气温 3°C 0°C ﹣2°C ﹣3°C
15.如果一个六棱柱的所有侧棱长之和是48cm,则它的侧棱长为 cm.
16.近似数4.609万精确到 位.
17.小明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测验的成绩是 .
18.在数轴上,表示﹣2的点与原点的距离是 .
19.计算﹣(﹣3)2的结果是 .
20.单项式a3b2的次数是 .
21.|x﹣3|=3﹣x,则x的取值范围是 .
22.如图:在桌上摆有一些大小相同的正方体木块,其从正面和从左面看到的形状图如图所示,则要摆出这样的图形至少需要 块正方体木块,至多需要 块正方体木块.
三.解答题
23.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是 (立方单位),表面积是 (平方单位)
(2)画出该几何体的主视图和左视图.
24.计算:
(1)2﹣(﹣3)+(+7)﹣9
(2)﹣4﹣2×32+(﹣2×32)
25.计算:
(1)﹣|﹣5|+(﹣3)3÷(﹣22)
(2)(﹣﹣)÷
26.如果规定符号“﹡”的意义是a﹡b=,
(1)求2﹡(﹣3)的值;
(2)求2﹡(﹣3)﹡4的值.
27.某一出租车一天下午以鼓楼为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:
+9,﹣3,﹣5,+4,﹣8,+6,﹣3,﹣6,﹣4,+10.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
28.右面是一个正方体纸盒的展开图,请把﹣10,7,10,﹣2,﹣7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数.
29.已知|x+1|=4,(y+2)2=4,求x+y的值.
参考答案与试题解析
一.选择题(共12小题)
1.比﹣2小1的数是( )
A.﹣3 B.﹣1 C.1 D.3
【分析】用﹣2减去1,然后根据有理数的减法运算法则进行计算即可得解.
【解答】解:﹣2﹣1=﹣(1+2)=﹣3.
故选:A.
2.国产科幻电影《流浪地球》上映17日,票房收入突破40亿元人民币,将40亿用科学记数法表示为( )
A.40×108 B.4×109 C.4×1010 D.0.4×1010
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:40亿用科学记数法表示为:4×109,
故选:B.
3.由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.9
【分析】根据三视图,该几何体的主视图以及俯视图可确定该几何体共有两层3列,故可得出该几何体的小正方体的个数.
【解答】解:综合三视图,我们可得出,这个几何体的底层应该有3个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体的小正方体的个数为3+1=4个,
故选:A.
4.如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与“看”相对的面上的汉字是( )
A.伦 B.奥 C.运 D.会
【分析】利用正方体及其表面展开图的特点解题.
【解答】解:这是一个正方体的平面展开图,共有六个面,
其中面“看”与面“运”相对,
面“伦”与面“奥”相对,
面“敦”与面“会”相对.
故选:C.
5.下列各数中最小的是( )
A.﹣5 B. C.0 D.﹣π
【分析】正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,据此判断出各数中最小的是哪个即可.
【解答】解:根据实数比较大小的方法,可得
﹣5<﹣π<0<,
∴各数中最小的是﹣5.
故选:A.
6.若8xmy与6x3yn的和是单项式,则m+n的值为( )
A.4 B.8 C.﹣4 D.﹣8
【分析】根据和是单项式,得到两式为同类项,利用同类项的定义求出m与n的值,即可求出所求.
【解答】解:∵8xmy与6x3yn的和是单项式,
∴m=3,n=1,
则m+n=3+1=4,
故选:A.
7.在下列几何体中,从正面看到为三角形的是( )
A. B. C. D.
【分析】主视图是从物体前面看,所得到的图形,再进行判断即可.
【解答】解:A、圆柱的主视图是长方形,故本选项不合题意;
B、三棱柱的主视图是长方形,故本选项不合题意;
C、正方体的主视图是正方形,故本选项不合题意;
D、圆锥的主视图是三角形,故本选项符合题意;
故选:D.
8.如图,甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是( )
A.仅有甲和乙相同 B.仅有甲和丙相同
C.仅有乙和丙相同 D.甲、乙、丙都相同
【分析】由已知条件可知,甲的主视图有2列,每列小正方数形数目分别为2,2;乙的主视图有2列,每列小正方数形数目分别为2,1;丙的主视图有2列,每列小正方数形数目分别为2,2.据此可即可求解.
【解答】解:根据分析可知,甲的主视图有2列,每列小正方数形数目分别为2,2;乙的主视图有2列,每列小正方数形数目分别为2,1;丙的主视图有2列,每列小正方数形数目分别为2,2;
则主视图相同的是甲和丙.
故选:B.
9.|﹣2019|=( )
A.2019 B.﹣2019 C. D.﹣
【分析】利用数轴上某个数与原点的距离叫做这个数的绝对值,进而得出答案.
【解答】解:|﹣2019|=2019.
故选:A.
10.计算下列各式,值最小的是( )
A.2×0+1﹣9 B.2+0×1﹣9 C.2+0﹣1×9 D.2+0+1﹣9
【分析】有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
【解答】解:A.2×0+1﹣9=﹣8,
B.2+0×1﹣9=﹣7
C.2+0﹣1×9=﹣7
D.2+0+1﹣9=﹣6,
故选:A.
11.用计算器计算230,按键顺序正确的是( )
A.
B.
C.
D.
【分析】根据计算器上各个键的功能和基本应用,即可得出答案.
【解答】解:按照计算器的基本应用,用计算器求230,按键顺序是2、xy、3、0、=;
故选:D.
12.如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )
A.点A的左边 B.点A与点B之间
C.点B与点C之间 D.点C的右边
【分析】根据绝对值是数轴上表示数的点到原点的距离,分别判断出点A、B、C到原点的距离的大小,从而得到原点的位置,即可得解.
【解答】解:∵|a|>|c|>|b|,
∴点A到原点的距离最大,点C其次,点B最小,
又∵AB=BC,
∴原点O的位置是在点B、C之间且靠近点B的地方.
故选:C.
二.填空题(共8小题)
13.子弹从枪膛中射出去的轨迹、汽车的雨刷把玻璃上的雨水刷干净,可分别看作是 点动成线 、 线动成面 的实际应用.
【分析】根据“点动成线,线动成面”直接回答即可.
【解答】解:子弹从枪膛中射出去的轨迹可以看作点动成线的实际应用;汽车的雨刷把玻璃上的雨水刷干净,可分别看作是线动成面的实际应用,
故答案为:点动成线,线动成面.
14.某地一周前四天每天的最高气温与最低气温如表,则这四天中温差最大的是 星期三 .
星期 一 二 三 四
最高气温 10°C 12°C 11°C 9°C
最低气温 3°C 0°C ﹣2°C ﹣3°C
【分析】先求出每天的温差,再比较大小,即可得出答案.
【解答】解:10﹣3=7,12﹣0=12,11﹣(﹣2)=13,9﹣(﹣3)=12,
∵7<12<13,
∴这四天中温差最大的是星期三,
故答案为:星期三.
15.如果一个六棱柱的所有侧棱长之和是48cm,则它的侧棱长为 8 cm.
【分析】六棱柱有6条侧棱,且每条侧棱的长度相等.
【解答】解:48÷6=8(cm).
故答案为:8.
16.近似数4.609万精确到 十 位.
【分析】根据“一个近似数精确到哪一位,即要看末位数字实际在哪一位”,4.609万=46090,9在十位,即可得到答案.
【解答】解:4.609万=46090,
9在十位,
即精确到十位,
故答案为:十.
17.小明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测验的成绩是 91分 .
【分析】根据题意列出算式,即可得出答案.
【解答】解:85+8﹣12+10=91,
即小明第四次测验的成绩是91分,
故答案为:91;
18.在数轴上,表示﹣2的点与原点的距离是 2 .
【分析】在数轴上,表示﹣2的点与原点的距离即是﹣2的绝对值,是2.
【解答】解:﹣2与原点的距离为:|﹣2|=2.
19.计算﹣(﹣3)2的结果是 ﹣8 .
【分析】直接利用有理数的混合运算法则计算得出答案.
【解答】解:原式=﹣9
=﹣8.
故答案为:﹣8.
20.单项式a3b2的次数是 5 .
【分析】根据单项式的次数的定义解答.
【解答】解:单项式a3b2的次数是3+2=5.
故答案为5.
21.|x﹣3|=3﹣x,则x的取值范围是 .
【考点】15:绝对值.
【专题】511:实数.
【分析】根据绝对值的意义,绝对值表示距离,所以3﹣x≥0,即可求解;
【解答】解:3﹣x≥0,
∴x≤3;
故答案为x≤3;
22.如图:在桌上摆有一些大小相同的正方体木块,其从正面和从左面看到的形状图如图所示,则要摆出这样的图形至少需要 块正方体木块,至多需要 块正方体木块.
【考点】U3:由三视图判断几何体.
【分析】利用从正面和从左面看到的形状图进而得出每层的最少与最多数量,进而得出答案.
【解答】解:易得第一层最少有4个正方体,最多有12个正方体;第二层最少有2个正方体,最多有4个,故最少有6个小正方形,至多要16块小正方体.
故答案为:6,16.
三.解答题
23.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是 5 (立方单位),表面积是 22 (平方单位)
(2)画出该几何体的主视图和左视图.
【考点】U4:作图﹣三视图.
【专题】13:作图题.
【分析】(1)几何体的体积为5个正方体的体积和,表面积为22个正方形的面积;
(2)主视图从左往右看3列正方形的个数依次为2,1,2;左视图1列正方形的个数为2.
【解答】解:(1)每个正方体的体积为1,∴组合几何体的体积为5×1=5;
∵组合几何体的前面和后面共有5×2=10个正方形,上下共有6个正方形,左右共6个正方形(外面4个加里面2个),每个正方形的面积为1,
∴组合几何体的表面积为22.
故答案为:5,22;
(2)作图如下:
24.计算:
(1)2﹣(﹣3)+(+7)﹣9
(2)﹣4﹣2×32+(﹣2×32)
【考点】1G:有理数的混合运算.
【专题】511:实数;66:运算能力.
【分析】(1)直接利用有理数的加减运算法则计算得出答案;
(2)直接利用有理数的混合运算法则计算得出答案.
【解答】解:(1)原式=2+3+7﹣9
=3;
(2)原式=﹣4﹣64﹣64
=﹣132.
25.计算:
(1)﹣|﹣5|+(﹣3)3÷(﹣22)
(2)(﹣﹣)÷
【考点】1G:有理数的混合运算.
【专题】511:实数;66:运算能力.
【分析】(1)原式先计算乘方及绝对值运算,再计算除法运算,最后算加减运算即可求出值;
(2)原式利用除法法则变形,计算即可求出值.
【解答】解:(1)原式=﹣5+27÷4=;
(2)原式=(﹣﹣)×=﹣×=﹣.
26.如果规定符号“﹡”的意义是a﹡b=,
(1)求2﹡(﹣3)的值;
(2)求2﹡(﹣3)﹡4的值.
【考点】1G:有理数的混合运算.
【专题】511:实数;66:运算能力.
【分析】(1)原式利用题中的新定义计算即可求出值;
(2)原式利用题中的新定义计算即可求出值.
【解答】解:(1)根据题中的新定义得:原式==6;
(2)根据题中的新定义得:原式==2.4.
27.某一出租车一天下午以鼓楼为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:
+9,﹣3,﹣5,+4,﹣8,+6,﹣3,﹣6,﹣4,+10.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
【考点】11:正数和负数.
【分析】(1)根据有理数的加法运算,可的计算结果,根据正数和负数,可得方向;
(2)根据行车就交费,可得营业额.
【解答】解:(1)9﹣3﹣5+4﹣8+6﹣3﹣6﹣4+10=0(千米)
答:将最后一名乘客送到目的地,出租车离鼓楼出发点0千米,在鼓楼处;
(2)(9+|﹣3|+|﹣5|+4+|﹣8|+6+|﹣3|+|﹣6|+|﹣4|+10)×2.4=139.2(元),
答:若每千米的价格为2.4元,司机一个下午的营业额是139.2元.
28.右面是一个正方体纸盒的展开图,请把﹣10,7,10,﹣2,﹣7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数.
【考点】I8:专题:正方体相对两个面上的文字.
【专题】26:开放型.
【分析】根据题意,找到相对的面,把数字填入即可.
【解答】解:根据相反数的定义将﹣10,7,﹣2分别填到10,﹣7,2的对面(答案不唯一),如:
29.已知|x+1|=4,(y+2)2=4,求x+y的值.
【考点】15:绝对值;19:有理数的加法;1E:有理数的乘方.
【专题】1:常规题型.
【分析】根据绝对值的性质与有理数的乘方求出x、y的值,然后代入代数式进行计算即可得解.
【解答】解:∵|x+1|=4,(y+2)2=4,
∴x+1=4,或x+1=﹣4,y+2=2或y+2=﹣2,
解得x=3或x=﹣5,y=0或y=﹣4,
∴x=3,y=0时,x+y=3+0=3;
x=3,y=﹣4时,x+y=3﹣4=﹣1;
x=﹣5,y=0时,x+y=﹣5+0=﹣5;
x=﹣5,y=﹣4时,x+y=﹣5﹣4=﹣9.
一.选择题(共12小题)
1.比﹣2小1的数是( )
A.﹣3 B.﹣1 C.1 D.3
2.国产科幻电影《流浪地球》上映17日,票房收入突破40亿元人民币,将40亿用科学记数法表示为( )
A.40×108 B.4×109 C.4×1010 D.0.4×1010
3.由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.9
4.如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与“看”相对的面上的汉字是( )
A.伦 B.奥 C.运 D.会
5.下列各数中最小的是( )
A.﹣5 B. C.0 D.﹣π
6.若8xmy与6x3yn的和是单项式,则m+n的值为( )
A.4 B.8 C.﹣4 D.﹣8
7.在下列几何体中,从正面看到为三角形的是( )
A. B. C. D.
8.如图,甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是( )
A.仅有甲和乙相同 B.仅有甲和丙相同
C.仅有乙和丙相同 D.甲、乙、丙都相同
9.|﹣2019|=( )
A.2019 B.﹣2019 C. D.﹣
10.计算下列各式,值最小的是( )
A.2×0+1﹣9 B.2+0×1﹣9 C.2+0﹣1×9 D.2+0+1﹣9
11.用计算器计算230,按键顺序正确的是( )
A.
B.
C.
D.
12.如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )
A.点A的左边 B.点A与点B之间
C.点B与点C之间 D.点C的右边
二.填空题(共8小题)
13.子弹从枪膛中射出去的轨迹、汽车的雨刷把玻璃上的雨水刷干净,可分别看作是 、 的实际应用.
14.某地一周前四天每天的最高气温与最低气温如表,则这四天中温差最大的是 .
星期 一 二 三 四
最高气温 10°C 12°C 11°C 9°C
最低气温 3°C 0°C ﹣2°C ﹣3°C
15.如果一个六棱柱的所有侧棱长之和是48cm,则它的侧棱长为 cm.
16.近似数4.609万精确到 位.
17.小明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测验的成绩是 .
18.在数轴上,表示﹣2的点与原点的距离是 .
19.计算﹣(﹣3)2的结果是 .
20.单项式a3b2的次数是 .
21.|x﹣3|=3﹣x,则x的取值范围是 .
22.如图:在桌上摆有一些大小相同的正方体木块,其从正面和从左面看到的形状图如图所示,则要摆出这样的图形至少需要 块正方体木块,至多需要 块正方体木块.
三.解答题
23.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是 (立方单位),表面积是 (平方单位)
(2)画出该几何体的主视图和左视图.
24.计算:
(1)2﹣(﹣3)+(+7)﹣9
(2)﹣4﹣2×32+(﹣2×32)
25.计算:
(1)﹣|﹣5|+(﹣3)3÷(﹣22)
(2)(﹣﹣)÷
26.如果规定符号“﹡”的意义是a﹡b=,
(1)求2﹡(﹣3)的值;
(2)求2﹡(﹣3)﹡4的值.
27.某一出租车一天下午以鼓楼为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:
+9,﹣3,﹣5,+4,﹣8,+6,﹣3,﹣6,﹣4,+10.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
28.右面是一个正方体纸盒的展开图,请把﹣10,7,10,﹣2,﹣7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数.
29.已知|x+1|=4,(y+2)2=4,求x+y的值.
参考答案与试题解析
一.选择题(共12小题)
1.比﹣2小1的数是( )
A.﹣3 B.﹣1 C.1 D.3
【分析】用﹣2减去1,然后根据有理数的减法运算法则进行计算即可得解.
【解答】解:﹣2﹣1=﹣(1+2)=﹣3.
故选:A.
2.国产科幻电影《流浪地球》上映17日,票房收入突破40亿元人民币,将40亿用科学记数法表示为( )
A.40×108 B.4×109 C.4×1010 D.0.4×1010
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:40亿用科学记数法表示为:4×109,
故选:B.
3.由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.9
【分析】根据三视图,该几何体的主视图以及俯视图可确定该几何体共有两层3列,故可得出该几何体的小正方体的个数.
【解答】解:综合三视图,我们可得出,这个几何体的底层应该有3个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体的小正方体的个数为3+1=4个,
故选:A.
4.如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与“看”相对的面上的汉字是( )
A.伦 B.奥 C.运 D.会
【分析】利用正方体及其表面展开图的特点解题.
【解答】解:这是一个正方体的平面展开图,共有六个面,
其中面“看”与面“运”相对,
面“伦”与面“奥”相对,
面“敦”与面“会”相对.
故选:C.
5.下列各数中最小的是( )
A.﹣5 B. C.0 D.﹣π
【分析】正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,据此判断出各数中最小的是哪个即可.
【解答】解:根据实数比较大小的方法,可得
﹣5<﹣π<0<,
∴各数中最小的是﹣5.
故选:A.
6.若8xmy与6x3yn的和是单项式,则m+n的值为( )
A.4 B.8 C.﹣4 D.﹣8
【分析】根据和是单项式,得到两式为同类项,利用同类项的定义求出m与n的值,即可求出所求.
【解答】解:∵8xmy与6x3yn的和是单项式,
∴m=3,n=1,
则m+n=3+1=4,
故选:A.
7.在下列几何体中,从正面看到为三角形的是( )
A. B. C. D.
【分析】主视图是从物体前面看,所得到的图形,再进行判断即可.
【解答】解:A、圆柱的主视图是长方形,故本选项不合题意;
B、三棱柱的主视图是长方形,故本选项不合题意;
C、正方体的主视图是正方形,故本选项不合题意;
D、圆锥的主视图是三角形,故本选项符合题意;
故选:D.
8.如图,甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是( )
A.仅有甲和乙相同 B.仅有甲和丙相同
C.仅有乙和丙相同 D.甲、乙、丙都相同
【分析】由已知条件可知,甲的主视图有2列,每列小正方数形数目分别为2,2;乙的主视图有2列,每列小正方数形数目分别为2,1;丙的主视图有2列,每列小正方数形数目分别为2,2.据此可即可求解.
【解答】解:根据分析可知,甲的主视图有2列,每列小正方数形数目分别为2,2;乙的主视图有2列,每列小正方数形数目分别为2,1;丙的主视图有2列,每列小正方数形数目分别为2,2;
则主视图相同的是甲和丙.
故选:B.
9.|﹣2019|=( )
A.2019 B.﹣2019 C. D.﹣
【分析】利用数轴上某个数与原点的距离叫做这个数的绝对值,进而得出答案.
【解答】解:|﹣2019|=2019.
故选:A.
10.计算下列各式,值最小的是( )
A.2×0+1﹣9 B.2+0×1﹣9 C.2+0﹣1×9 D.2+0+1﹣9
【分析】有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
【解答】解:A.2×0+1﹣9=﹣8,
B.2+0×1﹣9=﹣7
C.2+0﹣1×9=﹣7
D.2+0+1﹣9=﹣6,
故选:A.
11.用计算器计算230,按键顺序正确的是( )
A.
B.
C.
D.
【分析】根据计算器上各个键的功能和基本应用,即可得出答案.
【解答】解:按照计算器的基本应用,用计算器求230,按键顺序是2、xy、3、0、=;
故选:D.
12.如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )
A.点A的左边 B.点A与点B之间
C.点B与点C之间 D.点C的右边
【分析】根据绝对值是数轴上表示数的点到原点的距离,分别判断出点A、B、C到原点的距离的大小,从而得到原点的位置,即可得解.
【解答】解:∵|a|>|c|>|b|,
∴点A到原点的距离最大,点C其次,点B最小,
又∵AB=BC,
∴原点O的位置是在点B、C之间且靠近点B的地方.
故选:C.
二.填空题(共8小题)
13.子弹从枪膛中射出去的轨迹、汽车的雨刷把玻璃上的雨水刷干净,可分别看作是 点动成线 、 线动成面 的实际应用.
【分析】根据“点动成线,线动成面”直接回答即可.
【解答】解:子弹从枪膛中射出去的轨迹可以看作点动成线的实际应用;汽车的雨刷把玻璃上的雨水刷干净,可分别看作是线动成面的实际应用,
故答案为:点动成线,线动成面.
14.某地一周前四天每天的最高气温与最低气温如表,则这四天中温差最大的是 星期三 .
星期 一 二 三 四
最高气温 10°C 12°C 11°C 9°C
最低气温 3°C 0°C ﹣2°C ﹣3°C
【分析】先求出每天的温差,再比较大小,即可得出答案.
【解答】解:10﹣3=7,12﹣0=12,11﹣(﹣2)=13,9﹣(﹣3)=12,
∵7<12<13,
∴这四天中温差最大的是星期三,
故答案为:星期三.
15.如果一个六棱柱的所有侧棱长之和是48cm,则它的侧棱长为 8 cm.
【分析】六棱柱有6条侧棱,且每条侧棱的长度相等.
【解答】解:48÷6=8(cm).
故答案为:8.
16.近似数4.609万精确到 十 位.
【分析】根据“一个近似数精确到哪一位,即要看末位数字实际在哪一位”,4.609万=46090,9在十位,即可得到答案.
【解答】解:4.609万=46090,
9在十位,
即精确到十位,
故答案为:十.
17.小明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测验的成绩是 91分 .
【分析】根据题意列出算式,即可得出答案.
【解答】解:85+8﹣12+10=91,
即小明第四次测验的成绩是91分,
故答案为:91;
18.在数轴上,表示﹣2的点与原点的距离是 2 .
【分析】在数轴上,表示﹣2的点与原点的距离即是﹣2的绝对值,是2.
【解答】解:﹣2与原点的距离为:|﹣2|=2.
19.计算﹣(﹣3)2的结果是 ﹣8 .
【分析】直接利用有理数的混合运算法则计算得出答案.
【解答】解:原式=﹣9
=﹣8.
故答案为:﹣8.
20.单项式a3b2的次数是 5 .
【分析】根据单项式的次数的定义解答.
【解答】解:单项式a3b2的次数是3+2=5.
故答案为5.
21.|x﹣3|=3﹣x,则x的取值范围是 .
【考点】15:绝对值.
【专题】511:实数.
【分析】根据绝对值的意义,绝对值表示距离,所以3﹣x≥0,即可求解;
【解答】解:3﹣x≥0,
∴x≤3;
故答案为x≤3;
22.如图:在桌上摆有一些大小相同的正方体木块,其从正面和从左面看到的形状图如图所示,则要摆出这样的图形至少需要 块正方体木块,至多需要 块正方体木块.
【考点】U3:由三视图判断几何体.
【分析】利用从正面和从左面看到的形状图进而得出每层的最少与最多数量,进而得出答案.
【解答】解:易得第一层最少有4个正方体,最多有12个正方体;第二层最少有2个正方体,最多有4个,故最少有6个小正方形,至多要16块小正方体.
故答案为:6,16.
三.解答题
23.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是 5 (立方单位),表面积是 22 (平方单位)
(2)画出该几何体的主视图和左视图.
【考点】U4:作图﹣三视图.
【专题】13:作图题.
【分析】(1)几何体的体积为5个正方体的体积和,表面积为22个正方形的面积;
(2)主视图从左往右看3列正方形的个数依次为2,1,2;左视图1列正方形的个数为2.
【解答】解:(1)每个正方体的体积为1,∴组合几何体的体积为5×1=5;
∵组合几何体的前面和后面共有5×2=10个正方形,上下共有6个正方形,左右共6个正方形(外面4个加里面2个),每个正方形的面积为1,
∴组合几何体的表面积为22.
故答案为:5,22;
(2)作图如下:
24.计算:
(1)2﹣(﹣3)+(+7)﹣9
(2)﹣4﹣2×32+(﹣2×32)
【考点】1G:有理数的混合运算.
【专题】511:实数;66:运算能力.
【分析】(1)直接利用有理数的加减运算法则计算得出答案;
(2)直接利用有理数的混合运算法则计算得出答案.
【解答】解:(1)原式=2+3+7﹣9
=3;
(2)原式=﹣4﹣64﹣64
=﹣132.
25.计算:
(1)﹣|﹣5|+(﹣3)3÷(﹣22)
(2)(﹣﹣)÷
【考点】1G:有理数的混合运算.
【专题】511:实数;66:运算能力.
【分析】(1)原式先计算乘方及绝对值运算,再计算除法运算,最后算加减运算即可求出值;
(2)原式利用除法法则变形,计算即可求出值.
【解答】解:(1)原式=﹣5+27÷4=;
(2)原式=(﹣﹣)×=﹣×=﹣.
26.如果规定符号“﹡”的意义是a﹡b=,
(1)求2﹡(﹣3)的值;
(2)求2﹡(﹣3)﹡4的值.
【考点】1G:有理数的混合运算.
【专题】511:实数;66:运算能力.
【分析】(1)原式利用题中的新定义计算即可求出值;
(2)原式利用题中的新定义计算即可求出值.
【解答】解:(1)根据题中的新定义得:原式==6;
(2)根据题中的新定义得:原式==2.4.
27.某一出租车一天下午以鼓楼为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:
+9,﹣3,﹣5,+4,﹣8,+6,﹣3,﹣6,﹣4,+10.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
【考点】11:正数和负数.
【分析】(1)根据有理数的加法运算,可的计算结果,根据正数和负数,可得方向;
(2)根据行车就交费,可得营业额.
【解答】解:(1)9﹣3﹣5+4﹣8+6﹣3﹣6﹣4+10=0(千米)
答:将最后一名乘客送到目的地,出租车离鼓楼出发点0千米,在鼓楼处;
(2)(9+|﹣3|+|﹣5|+4+|﹣8|+6+|﹣3|+|﹣6|+|﹣4|+10)×2.4=139.2(元),
答:若每千米的价格为2.4元,司机一个下午的营业额是139.2元.
28.右面是一个正方体纸盒的展开图,请把﹣10,7,10,﹣2,﹣7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数.
【考点】I8:专题:正方体相对两个面上的文字.
【专题】26:开放型.
【分析】根据题意,找到相对的面,把数字填入即可.
【解答】解:根据相反数的定义将﹣10,7,﹣2分别填到10,﹣7,2的对面(答案不唯一),如:
29.已知|x+1|=4,(y+2)2=4,求x+y的值.
【考点】15:绝对值;19:有理数的加法;1E:有理数的乘方.
【专题】1:常规题型.
【分析】根据绝对值的性质与有理数的乘方求出x、y的值,然后代入代数式进行计算即可得解.
【解答】解:∵|x+1|=4,(y+2)2=4,
∴x+1=4,或x+1=﹣4,y+2=2或y+2=﹣2,
解得x=3或x=﹣5,y=0或y=﹣4,
∴x=3,y=0时,x+y=3+0=3;
x=3,y=﹣4时,x+y=3﹣4=﹣1;
x=﹣5,y=0时,x+y=﹣5+0=﹣5;
x=﹣5,y=﹣4时,x+y=﹣5﹣4=﹣9.
同课章节目录
