山东省淄博市临淄区2019-2020学年六年级(上)期中数学试卷(五四学制) (解析版)
文档属性
| 名称 | 山东省淄博市临淄区2019-2020学年六年级(上)期中数学试卷(五四学制) (解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 235.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-04 00:00:00 | ||
图片预览




文档简介
2019-2020学年六年级(上)期中数学试卷
一.选择题(共12小题)
1.﹣的倒数是( )
A.﹣2 B. C.2 D.﹣
2.如图是一个几何体的三视图,则这个几何体是( )
A.正方体 B.长方体 C.三棱柱 D.三棱锥
3.在市委、市府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字应是( )
A.全 B.明 C.城 D.国
4.某小区居民王先生改进用水设施,在5年内帮助他居住小区的居民累计节水39400吨,将39400用科学记数法表示(结果保留2个有效数字)应为( )
A.3.9×104 B.3.94×104 C.39.4×103 D.4.0×104
5.如下图,下列平面图形能折成一个棱柱的是( )
A.①② B.②③ C.②④ D.②③④
6.如图是由六个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )
A.从正面看改变,从左面看改变
B.从上面看不变,从左面看不变
C.从上面看改变,从左面看改变
D.从正面看改变,从左面看不变
7.以下四个选项表示某天四个城市的平均气温,其中平均气温最低的是( )
A.﹣3℃ B.15℃ C.﹣10℃ D.﹣1℃
8.某大米包装袋上标注着“净含量:10kg±150g”,那么随意从这种牌子的大米中取出一袋,这袋大米的最大质量为( )
A.150g B.9.85kg C.10.15kg D.12kg
9.从正面、左面、上面观察一个由小正方体构成的几何体依次得到以下的形状图,那么构成这个几何体的小正方体有( )
A.4个 B.5个 C.6个 D.7个
10.在算式4﹣|﹣3□5|中的□所在位置,填入下列哪种运算符号,计算出来的值最小( )
A.+ B.﹣ C.× D.÷
11.如图,四幅图是一个正方体不同的侧面,六个面上分别写着A,B,C,D,E,F,则C,A,E的对面字母分别是(标注的三个面是前面、上面、右面)( )
A.F,B,D B.D,F,B C.B,F,D D.B,D,F
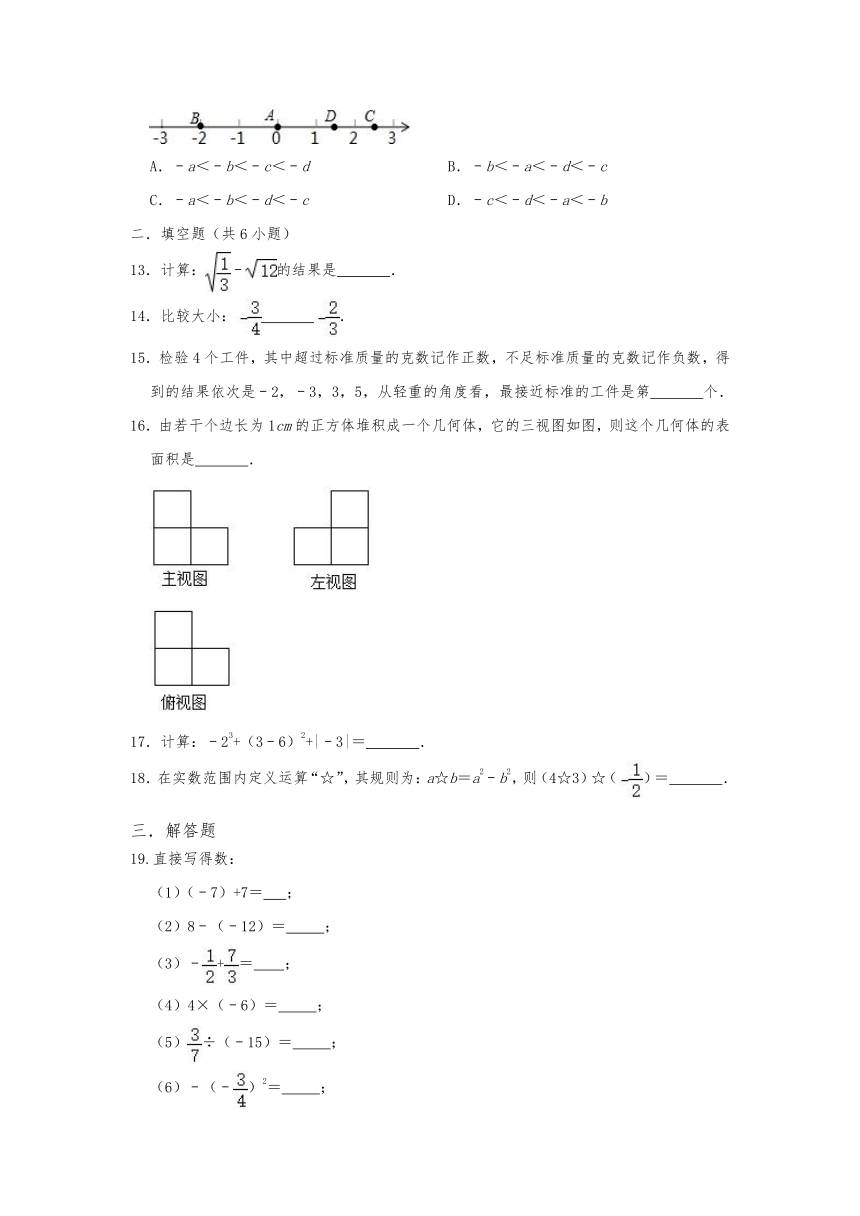
12.如图所示,A、B、C、D四点在数轴上分别表示有理数a、b、c、d,则大小顺序正确的是( )
A.﹣a<﹣b<﹣c<﹣d B.﹣b<﹣a<﹣d<﹣c
C.﹣a<﹣b<﹣d<﹣c D.﹣c<﹣d<﹣a<﹣b
二.填空题(共6小题)
13.计算:﹣的结果是 .
14.比较大小: .
15.检验4个工件,其中超过标准质量的克数记作正数,不足标准质量的克数记作负数,得到的结果依次是﹣2,﹣3,3,5,从轻重的角度看,最接近标准的工件是第 个.
16.由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是 .
17.计算:﹣23+(3﹣6)2+|﹣3|= .
18.在实数范围内定义运算“☆”,其规则为:a☆b=a2﹣b2,则(4☆3)☆()= .
三.解答题
19.直接写得数:
(1)(﹣7)+7= ;
(2)8﹣(﹣12)= ;
(3)﹣+= ;
(4)4×(﹣6)= ;
(5)÷(﹣15)= ;
(6)﹣(﹣)2= ;
20.计算:
(1)﹣|1﹣2|﹣(﹣2)﹣22
(2)(﹣0.8)+1.2+(﹣0.7)+(﹣2.1)+0.8+3.5
(3)﹣3×2+(﹣2)2﹣5
(4)
(5)(﹣1)+(﹣6)+(﹣2)+
(6)25﹣3×[32+2×(﹣3)]+5.
(7)
(8)(﹣)×(﹣3)÷(﹣1)÷3
(9)
(10)
21.如图,这是一个由小立方块塔成的几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请你画出它从正面和从左面看到的形状图.
22.下表是某中学七年级5名学生的体重情况,试完成下表
姓名 小颖 小明 小刚 小京 小宁
体重(千克) 34 45
体重与平均体重的差 ﹣7 +3 ﹣4 0
(1)谁最重?谁最轻?
(2)最重的与最轻的相差多少?
23.有8箱橘子,以每箱15kg为标准,超过的千克数记为正数,不足的千克数记为负数,现记录如下(单位:千克):1.2,﹣0.8,2.3,1.7,﹣1.5,﹣2.7,2,﹣0.2,则这8箱橘子的总重量是多少?
24.某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶纪录如下(单位:千米):+10,﹣9,+7,﹣15,+6,﹣14,+4,﹣2
(1)A在岗亭何方?距岗亭多远?
(2)若摩托车行驶1千米耗油0.05升,这一天共耗油多少升?
25.如图是由棱长为1的小正方体堆砌成的几何体,
(1)画出这个几何体从正面、左面、上面看到的形状图;
(2)求堆砌成的几何体的表面积;
(3)求堆砌成的几何体的棱长.
26.已知一个圆柱的侧面展开图为如图所示的矩形,它的一个底面圆的面积为多少?
参考答案与试题解析
一.选择题(共12小题)
1.﹣的倒数是( )
A.﹣2 B. C.2 D.﹣
【分析】根据乘积为1的两个数互为倒数,可得一个数的倒数.
【解答】解:﹣的倒数是﹣2,
故选:A.
2.如图是一个几何体的三视图,则这个几何体是( )
A.正方体 B.长方体 C.三棱柱 D.三棱锥
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:根据主视图和左视图为矩形是柱体,根据俯视图是正方形可判断出这个几何体应该是长方体.
故选:B.
3.在市委、市府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字应是( )
A.全 B.明 C.城 D.国
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:由正方体的展开图特点可得:与“文”字所在的面上标的字应是“城”.
故选:C.
4.某小区居民王先生改进用水设施,在5年内帮助他居住小区的居民累计节水39400吨,将39400用科学记数法表示(结果保留2个有效数字)应为( )
A.3.9×104 B.3.94×104 C.39.4×103 D.4.0×104
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于39400有5位,所以可以确定n=5﹣1=4,由于结果保留2个有效数字,所以a=3.9.
【解答】解:39 400≈3.9×104.
故选:A.
5.如下图,下列平面图形能折成一个棱柱的是( )
A.①② B.②③ C.②④ D.②③④
【分析】由四棱柱四个侧面和上下两个底面的特征作答.
【解答】解:由四棱柱四个侧面和上下两个底面的特征可知,②③④都能折成一个四棱柱,而①中的侧面缺少一个长方形.故选D.
6.如图是由六个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )
A.从正面看改变,从左面看改变
B.从上面看不变,从左面看不变
C.从上面看改变,从左面看改变
D.从正面看改变,从左面看不变
【分析】根据从正面看得到的图形是主视图,从上面看得到的图形是俯视图,从左边看得到的图形是左视图,可得答案.
【解答】解:由六个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体的主视图改变,俯视图改变,左视图不变,
故选:D.
7.以下四个选项表示某天四个城市的平均气温,其中平均气温最低的是( )
A.﹣3℃ B.15℃ C.﹣10℃ D.﹣1℃
【分析】根据正数大于零,零大于负数,两个负数比较大小,绝对值大的负数反而小,可得答案.
【解答】解:15℃>﹣1℃>﹣3℃>﹣10℃,
故选:C.
8.某大米包装袋上标注着“净含量:10kg±150g”,那么随意从这种牌子的大米中取出一袋,这袋大米的最大质量为( )
A.150g B.9.85kg C.10.15kg D.12kg
【分析】首先审清题意,明确“正”和“负”所表示的意义;再根据题意作答.
【解答】解:150g=0.15kg,
10+0.15=10.15,
∴这袋大米的最大质量为10.15kg.
故选:C.
9.从正面、左面、上面观察一个由小正方体构成的几何体依次得到以下的形状图,那么构成这个几何体的小正方体有( )
A.4个 B.5个 C.6个 D.7个
【分析】易得这个几何体共有2层,由俯视图可得第一层正方体的个数,由主视图和左视图可得第二层正方体的个数,相加即可.
【解答】解:由从上面看到的图形易得最底层有4个正方体,第二层有1个正方体,
那么共有4+1=5(个)正方体.
故选:B.
10.在算式4﹣|﹣3□5|中的□所在位置,填入下列哪种运算符号,计算出来的值最小( )
A.+ B.﹣ C.× D.÷
【分析】本题是要求两数差的最小值,由于被减数一定,当减数最大时,差最小.故要使计算出来的值最小,只要绝对值最大,故填入“×”时即可.
【解答】解:将符号代入:
A、4﹣|﹣3+5|=2;
B、4﹣|﹣3﹣5|=﹣4;
C、4﹣|﹣3×5|=﹣11;
D、4﹣|﹣3÷5|=;
所以填入×号时,计算出来的值最小.
故选:C.
11.如图,四幅图是一个正方体不同的侧面,六个面上分别写着A,B,C,D,E,F,则C,A,E的对面字母分别是(标注的三个面是前面、上面、右面)( )
A.F,B,D B.D,F,B C.B,F,D D.B,D,F
【分析】根据与E相邻的面为A、C、D、F可知E与B相对,根据与F相邻的面有B、C、D、E可知F与A相对,然后判断出C、D相对,从而得解.
【解答】解:由图可知,与E相邻的面为A、C、D、F,
所以E与B相对,
与F相邻的面有B、C、D、E,
所以F与A相对,
所以C、D相对,
所以C、A、E的对面字母分别是D、F、B.
故选:B.
12.如图所示,A、B、C、D四点在数轴上分别表示有理数a、b、c、d,则大小顺序正确的是( )
A.﹣a<﹣b<﹣c<﹣d B.﹣b<﹣a<﹣d<﹣c
C.﹣a<﹣b<﹣d<﹣c D.﹣c<﹣d<﹣a<﹣b
【分析】根据数轴得到b<a<d<c,根据有理数的大小比较法则判断.
【解答】解:由数轴可知,b<a<d<c,
则﹣c<﹣d<﹣a<﹣b,
故选:D.
二.填空题(共6小题)
13.计算:﹣的结果是 ﹣ .
【分析】先化为最简二次根式,然后合并.
【解答】解:原式=﹣2=﹣.
故答案为:﹣.
14.比较大小: < .
【分析】先计算|﹣|==,|﹣|==,然后根据负数的绝对值越大,这个数越小进行大小比较.
【解答】解:∵|﹣|==,|﹣|==,
∴﹣<﹣.
故答案为<.
15.检验4个工件,其中超过标准质量的克数记作正数,不足标准质量的克数记作负数,得到的结果依次是﹣2,﹣3,3,5,从轻重的角度看,最接近标准的工件是第 1 个.
【分析】比较各个工件克数的绝对值,绝对值最小的工件最接近标准,从而得出结论.
【解答】解:因为|﹣2|=2,|﹣3|=3,|3|=3,|5|=5,
由于|﹣2|最小,所以从轻重的角度看,质量是﹣2的工件最接近标准工件.
故答案:1
16.由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是 18cm2 .
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:综合三视图,我们可以得出,这个几何模型的底层有2+1=3个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是3+1=4个.
所以表面积为3×6=18cm2.
故答案为:18cm2.
17.计算:﹣23+(3﹣6)2+|﹣3|= 4 .
【分析】根据有理数的混合运算顺序和运算法则计算可得.
【解答】解:原式=﹣8+9+3=4,
故答案为:4.
18.在实数范围内定义运算“☆”,其规则为:a☆b=a2﹣b2,则(4☆3)☆()= 48 .
【分析】原式利用已知的新定义计算即可求出值.
【解答】解:根据题中的新定义得:原式=7☆()=49﹣=48,
故答案为:48
三.解答题
19.直接写得数:
(1)(﹣7)+7= ;
(2)8﹣(﹣12)= ;
(3)﹣+= ;
(4)4×(﹣6)= ;
(5)÷(﹣15)= ;
(6)﹣(﹣)2= ;
【考点】1G:有理数的混合运算.
【专题】511:实数;66:运算能力.
【分析】(1)根据加法法则计算可得;
(2)根据有理数的减法法则算可得;
(3)通分后利用加法法则计算可得;
(4)利用有理数的乘法法则计算可得;
(5)除法转化为乘法,再进一步计算可得;
(6)根据乘方的运算法则计算可得.
【解答】解:(1)(﹣7)+7=﹣(7﹣7)=0;
(2)8﹣(﹣12)=8+12=20;
(3)原式=﹣+=;
(4)4×(﹣6)=﹣24;
(5)原式=×(﹣)=﹣;
(6)原式=﹣;
故答案为:(1)0;(2)20;(3);(4)﹣24;(5);(6).
20.计算:
(1)﹣|1﹣2|﹣(﹣2)﹣22
(2)(﹣0.8)+1.2+(﹣0.7)+(﹣2.1)+0.8+3.5
(3)﹣3×2+(﹣2)2﹣5
(4)
(5)(﹣1)+(﹣6)+(﹣2)+
(6)25﹣3×[32+2×(﹣3)]+5.
(7)
(8)(﹣)×(﹣3)÷(﹣1)÷3
(9)
(10)
【考点】1G:有理数的混合运算.
【专题】511:实数;66:运算能力.
【分析】(1)原式利用减法法则变形,计算即可求出值;
(2)原式结合后,相加即可求出值;
(3)原式先计算乘方及乘法运算,再计算加减运算即可求出值;
(4)原式结合后,相加即可求出值;
(5)原式结合后,相加即可求出值;
(6)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可求出值;
(7)原式逆用乘法分配律计算即可求出值;
(8)原式从左到右依次计算即可求出值;
(9)原式先计算乘方运算,再计算乘除运算即可求出值;
(10)原式利用乘法分配律计算即可求出值.
【解答】解:(1)原式=﹣1+2﹣4=﹣3;
(2)原式=﹣0.8+0.8﹣0.7﹣2.1+1.2+3.5=1.9;
(3)原式=﹣6+4﹣5=﹣7;
(4)原式=1+﹣1﹣3﹣1=3﹣5﹣1=﹣3;
(5)原式=﹣1﹣2﹣6+=﹣4﹣3=﹣7;
(6)原式=25﹣3×(9﹣6)+5=25﹣9+5=21;
(7)原式=﹣×(3.2+6.8)=﹣×10=﹣3;
(8)原式=﹣×××=﹣;
(9)原式=﹣8××(﹣)=;
(10)原式=﹣32+12+18﹣10=﹣12.
21.如图,这是一个由小立方块塔成的几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请你画出它从正面和从左面看到的形状图.
【考点】U2:简单组合体的三视图;U4:作图﹣三视图.
【专题】55F:投影与视图.
【分析】由已知条件可知,主视图有3列,每列小正方形数目分别为3,2,4;左视图有3列,每列小正方形数目分别为2,3,4,据此可画出图形.
【解答】解:如图所示:
22.下表是某中学七年级5名学生的体重情况,试完成下表
姓名 小颖 小明 小刚 小京 小宁
体重(千克) 34 45
体重与平均体重的差 ﹣7 +3 ﹣4 0
(1)谁最重?谁最轻?
(2)最重的与最轻的相差多少?
【考点】18:有理数大小比较;1B:有理数的加减混合运算.
【专题】11:计算题.
【分析】(1)由小颖的体重与体重和平均体重的差,求出平均体重,进而确定出其他人的题中,填表后,找出最重的与最轻的即可;
(2)用最重的减去最轻的列出算式,计算即可得到结果.
【解答】解:(1)由小颖体重为34千克,体重与平均体重的差为﹣7,得到平均体重为34﹣(﹣7)=34+7=41(千克),
则小明的体重为41+3=44(千克);小刚的体重为44千克;小京的体重为41+(﹣4)=37(千克);小宁的体重为41千克,填表如下:
姓名 小颖 小明 小刚 小京 小宁
体重(千克) 34 44 45 37 41
体重与平均体重的差 ﹣7 +3 +4 ﹣4 0
∴小刚的体重最重;小颖的体重最轻;
(2)最重与最轻相差为45﹣34=11(千克).
23.有8箱橘子,以每箱15kg为标准,超过的千克数记为正数,不足的千克数记为负数,现记录如下(单位:千克):1.2,﹣0.8,2.3,1.7,﹣1.5,﹣2.7,2,﹣0.2,则这8箱橘子的总重量是多少?
【考点】11:正数和负数.
【分析】根据有理数的加法运算,可得答案.
【解答】1.2+(﹣0.8)+2.3+1.7+(﹣1.5)+(﹣2.7)+2+(﹣0.2)=1.2﹣0.8+2.3+1.7
﹣1.5﹣2.7+2﹣0.2
=(2.3+1.7+2)+(﹣0.8﹣2.7﹣1.5)+(1.2﹣0.2)
=6﹣5+1=2(kg).
则15×8+2=122(kg).
答:这8箱橘子的总重量是122千克.
24.某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶纪录如下(单位:千米):+10,﹣9,+7,﹣15,+6,﹣14,+4,﹣2
(1)A在岗亭何方?距岗亭多远?
(2)若摩托车行驶1千米耗油0.05升,这一天共耗油多少升?
【考点】11:正数和负数.
【分析】(1)根据有理数的加法运算,可得和,再根据和的大小,向北记为正,可判断位置;
(2)根据行车就耗油,可得总耗油量.
【解答】解:(1)10+(﹣9)+7+(﹣15)+6+(﹣14)+4+(﹣2)=﹣13,
答:A在岗亭南方,距岗亭13(千米);
(2)(10++7++6++4+)×0.05=3.35(升),
答:这一天共耗油3.35升.
25.如图是由棱长为1的小正方体堆砌成的几何体,
(1)画出这个几何体从正面、左面、上面看到的形状图;
(2)求堆砌成的几何体的表面积;
(3)求堆砌成的几何体的棱长.
【考点】I4:几何体的表面积;U4:作图﹣三视图.
【专题】55F:投影与视图;64:几何直观.
【分析】(1)直接利用三视图的画法进而得出答案;
(2)直接利用几何体的形状进而得出其表面;
(3)直接利用几何体的形状进而得出几何体的棱长.
【解答】解:(1)如图所示:
(2)堆砌成的几何体的表面积为:3+3+2+2+2+2=14;
(3)堆砌成的几何体的棱长为:22.
26.已知一个圆柱的侧面展开图为如图所示的矩形,它的一个底面圆的面积为多少?
【考点】I6:几何体的展开图.
【专题】55C:与圆有关的计算;64:几何直观.
【分析】分底面周长为4π和2π两种情况讨论,先求得底面半径,再根据圆的面积公式即可求解.
【解答】解:①底面周长为4π时,半径为4π÷π÷2=2,底面圆的面积为π×22=4π;
②底面周长为2π时,半径为2π÷π÷2=1,底面圆的面积为π×12=π.
故它的一个底面圆的面积为π或4π.
一.选择题(共12小题)
1.﹣的倒数是( )
A.﹣2 B. C.2 D.﹣
2.如图是一个几何体的三视图,则这个几何体是( )
A.正方体 B.长方体 C.三棱柱 D.三棱锥
3.在市委、市府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字应是( )
A.全 B.明 C.城 D.国
4.某小区居民王先生改进用水设施,在5年内帮助他居住小区的居民累计节水39400吨,将39400用科学记数法表示(结果保留2个有效数字)应为( )
A.3.9×104 B.3.94×104 C.39.4×103 D.4.0×104
5.如下图,下列平面图形能折成一个棱柱的是( )
A.①② B.②③ C.②④ D.②③④
6.如图是由六个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )
A.从正面看改变,从左面看改变
B.从上面看不变,从左面看不变
C.从上面看改变,从左面看改变
D.从正面看改变,从左面看不变
7.以下四个选项表示某天四个城市的平均气温,其中平均气温最低的是( )
A.﹣3℃ B.15℃ C.﹣10℃ D.﹣1℃
8.某大米包装袋上标注着“净含量:10kg±150g”,那么随意从这种牌子的大米中取出一袋,这袋大米的最大质量为( )
A.150g B.9.85kg C.10.15kg D.12kg
9.从正面、左面、上面观察一个由小正方体构成的几何体依次得到以下的形状图,那么构成这个几何体的小正方体有( )
A.4个 B.5个 C.6个 D.7个
10.在算式4﹣|﹣3□5|中的□所在位置,填入下列哪种运算符号,计算出来的值最小( )
A.+ B.﹣ C.× D.÷
11.如图,四幅图是一个正方体不同的侧面,六个面上分别写着A,B,C,D,E,F,则C,A,E的对面字母分别是(标注的三个面是前面、上面、右面)( )
A.F,B,D B.D,F,B C.B,F,D D.B,D,F
12.如图所示,A、B、C、D四点在数轴上分别表示有理数a、b、c、d,则大小顺序正确的是( )
A.﹣a<﹣b<﹣c<﹣d B.﹣b<﹣a<﹣d<﹣c
C.﹣a<﹣b<﹣d<﹣c D.﹣c<﹣d<﹣a<﹣b
二.填空题(共6小题)
13.计算:﹣的结果是 .
14.比较大小: .
15.检验4个工件,其中超过标准质量的克数记作正数,不足标准质量的克数记作负数,得到的结果依次是﹣2,﹣3,3,5,从轻重的角度看,最接近标准的工件是第 个.
16.由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是 .
17.计算:﹣23+(3﹣6)2+|﹣3|= .
18.在实数范围内定义运算“☆”,其规则为:a☆b=a2﹣b2,则(4☆3)☆()= .
三.解答题
19.直接写得数:
(1)(﹣7)+7= ;
(2)8﹣(﹣12)= ;
(3)﹣+= ;
(4)4×(﹣6)= ;
(5)÷(﹣15)= ;
(6)﹣(﹣)2= ;
20.计算:
(1)﹣|1﹣2|﹣(﹣2)﹣22
(2)(﹣0.8)+1.2+(﹣0.7)+(﹣2.1)+0.8+3.5
(3)﹣3×2+(﹣2)2﹣5
(4)
(5)(﹣1)+(﹣6)+(﹣2)+
(6)25﹣3×[32+2×(﹣3)]+5.
(7)
(8)(﹣)×(﹣3)÷(﹣1)÷3
(9)
(10)
21.如图,这是一个由小立方块塔成的几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请你画出它从正面和从左面看到的形状图.
22.下表是某中学七年级5名学生的体重情况,试完成下表
姓名 小颖 小明 小刚 小京 小宁
体重(千克) 34 45
体重与平均体重的差 ﹣7 +3 ﹣4 0
(1)谁最重?谁最轻?
(2)最重的与最轻的相差多少?
23.有8箱橘子,以每箱15kg为标准,超过的千克数记为正数,不足的千克数记为负数,现记录如下(单位:千克):1.2,﹣0.8,2.3,1.7,﹣1.5,﹣2.7,2,﹣0.2,则这8箱橘子的总重量是多少?
24.某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶纪录如下(单位:千米):+10,﹣9,+7,﹣15,+6,﹣14,+4,﹣2
(1)A在岗亭何方?距岗亭多远?
(2)若摩托车行驶1千米耗油0.05升,这一天共耗油多少升?
25.如图是由棱长为1的小正方体堆砌成的几何体,
(1)画出这个几何体从正面、左面、上面看到的形状图;
(2)求堆砌成的几何体的表面积;
(3)求堆砌成的几何体的棱长.
26.已知一个圆柱的侧面展开图为如图所示的矩形,它的一个底面圆的面积为多少?
参考答案与试题解析
一.选择题(共12小题)
1.﹣的倒数是( )
A.﹣2 B. C.2 D.﹣
【分析】根据乘积为1的两个数互为倒数,可得一个数的倒数.
【解答】解:﹣的倒数是﹣2,
故选:A.
2.如图是一个几何体的三视图,则这个几何体是( )
A.正方体 B.长方体 C.三棱柱 D.三棱锥
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:根据主视图和左视图为矩形是柱体,根据俯视图是正方形可判断出这个几何体应该是长方体.
故选:B.
3.在市委、市府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字应是( )
A.全 B.明 C.城 D.国
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:由正方体的展开图特点可得:与“文”字所在的面上标的字应是“城”.
故选:C.
4.某小区居民王先生改进用水设施,在5年内帮助他居住小区的居民累计节水39400吨,将39400用科学记数法表示(结果保留2个有效数字)应为( )
A.3.9×104 B.3.94×104 C.39.4×103 D.4.0×104
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于39400有5位,所以可以确定n=5﹣1=4,由于结果保留2个有效数字,所以a=3.9.
【解答】解:39 400≈3.9×104.
故选:A.
5.如下图,下列平面图形能折成一个棱柱的是( )
A.①② B.②③ C.②④ D.②③④
【分析】由四棱柱四个侧面和上下两个底面的特征作答.
【解答】解:由四棱柱四个侧面和上下两个底面的特征可知,②③④都能折成一个四棱柱,而①中的侧面缺少一个长方形.故选D.
6.如图是由六个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )
A.从正面看改变,从左面看改变
B.从上面看不变,从左面看不变
C.从上面看改变,从左面看改变
D.从正面看改变,从左面看不变
【分析】根据从正面看得到的图形是主视图,从上面看得到的图形是俯视图,从左边看得到的图形是左视图,可得答案.
【解答】解:由六个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体的主视图改变,俯视图改变,左视图不变,
故选:D.
7.以下四个选项表示某天四个城市的平均气温,其中平均气温最低的是( )
A.﹣3℃ B.15℃ C.﹣10℃ D.﹣1℃
【分析】根据正数大于零,零大于负数,两个负数比较大小,绝对值大的负数反而小,可得答案.
【解答】解:15℃>﹣1℃>﹣3℃>﹣10℃,
故选:C.
8.某大米包装袋上标注着“净含量:10kg±150g”,那么随意从这种牌子的大米中取出一袋,这袋大米的最大质量为( )
A.150g B.9.85kg C.10.15kg D.12kg
【分析】首先审清题意,明确“正”和“负”所表示的意义;再根据题意作答.
【解答】解:150g=0.15kg,
10+0.15=10.15,
∴这袋大米的最大质量为10.15kg.
故选:C.
9.从正面、左面、上面观察一个由小正方体构成的几何体依次得到以下的形状图,那么构成这个几何体的小正方体有( )
A.4个 B.5个 C.6个 D.7个
【分析】易得这个几何体共有2层,由俯视图可得第一层正方体的个数,由主视图和左视图可得第二层正方体的个数,相加即可.
【解答】解:由从上面看到的图形易得最底层有4个正方体,第二层有1个正方体,
那么共有4+1=5(个)正方体.
故选:B.
10.在算式4﹣|﹣3□5|中的□所在位置,填入下列哪种运算符号,计算出来的值最小( )
A.+ B.﹣ C.× D.÷
【分析】本题是要求两数差的最小值,由于被减数一定,当减数最大时,差最小.故要使计算出来的值最小,只要绝对值最大,故填入“×”时即可.
【解答】解:将符号代入:
A、4﹣|﹣3+5|=2;
B、4﹣|﹣3﹣5|=﹣4;
C、4﹣|﹣3×5|=﹣11;
D、4﹣|﹣3÷5|=;
所以填入×号时,计算出来的值最小.
故选:C.
11.如图,四幅图是一个正方体不同的侧面,六个面上分别写着A,B,C,D,E,F,则C,A,E的对面字母分别是(标注的三个面是前面、上面、右面)( )
A.F,B,D B.D,F,B C.B,F,D D.B,D,F
【分析】根据与E相邻的面为A、C、D、F可知E与B相对,根据与F相邻的面有B、C、D、E可知F与A相对,然后判断出C、D相对,从而得解.
【解答】解:由图可知,与E相邻的面为A、C、D、F,
所以E与B相对,
与F相邻的面有B、C、D、E,
所以F与A相对,
所以C、D相对,
所以C、A、E的对面字母分别是D、F、B.
故选:B.
12.如图所示,A、B、C、D四点在数轴上分别表示有理数a、b、c、d,则大小顺序正确的是( )
A.﹣a<﹣b<﹣c<﹣d B.﹣b<﹣a<﹣d<﹣c
C.﹣a<﹣b<﹣d<﹣c D.﹣c<﹣d<﹣a<﹣b
【分析】根据数轴得到b<a<d<c,根据有理数的大小比较法则判断.
【解答】解:由数轴可知,b<a<d<c,
则﹣c<﹣d<﹣a<﹣b,
故选:D.
二.填空题(共6小题)
13.计算:﹣的结果是 ﹣ .
【分析】先化为最简二次根式,然后合并.
【解答】解:原式=﹣2=﹣.
故答案为:﹣.
14.比较大小: < .
【分析】先计算|﹣|==,|﹣|==,然后根据负数的绝对值越大,这个数越小进行大小比较.
【解答】解:∵|﹣|==,|﹣|==,
∴﹣<﹣.
故答案为<.
15.检验4个工件,其中超过标准质量的克数记作正数,不足标准质量的克数记作负数,得到的结果依次是﹣2,﹣3,3,5,从轻重的角度看,最接近标准的工件是第 1 个.
【分析】比较各个工件克数的绝对值,绝对值最小的工件最接近标准,从而得出结论.
【解答】解:因为|﹣2|=2,|﹣3|=3,|3|=3,|5|=5,
由于|﹣2|最小,所以从轻重的角度看,质量是﹣2的工件最接近标准工件.
故答案:1
16.由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是 18cm2 .
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:综合三视图,我们可以得出,这个几何模型的底层有2+1=3个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是3+1=4个.
所以表面积为3×6=18cm2.
故答案为:18cm2.
17.计算:﹣23+(3﹣6)2+|﹣3|= 4 .
【分析】根据有理数的混合运算顺序和运算法则计算可得.
【解答】解:原式=﹣8+9+3=4,
故答案为:4.
18.在实数范围内定义运算“☆”,其规则为:a☆b=a2﹣b2,则(4☆3)☆()= 48 .
【分析】原式利用已知的新定义计算即可求出值.
【解答】解:根据题中的新定义得:原式=7☆()=49﹣=48,
故答案为:48
三.解答题
19.直接写得数:
(1)(﹣7)+7= ;
(2)8﹣(﹣12)= ;
(3)﹣+= ;
(4)4×(﹣6)= ;
(5)÷(﹣15)= ;
(6)﹣(﹣)2= ;
【考点】1G:有理数的混合运算.
【专题】511:实数;66:运算能力.
【分析】(1)根据加法法则计算可得;
(2)根据有理数的减法法则算可得;
(3)通分后利用加法法则计算可得;
(4)利用有理数的乘法法则计算可得;
(5)除法转化为乘法,再进一步计算可得;
(6)根据乘方的运算法则计算可得.
【解答】解:(1)(﹣7)+7=﹣(7﹣7)=0;
(2)8﹣(﹣12)=8+12=20;
(3)原式=﹣+=;
(4)4×(﹣6)=﹣24;
(5)原式=×(﹣)=﹣;
(6)原式=﹣;
故答案为:(1)0;(2)20;(3);(4)﹣24;(5);(6).
20.计算:
(1)﹣|1﹣2|﹣(﹣2)﹣22
(2)(﹣0.8)+1.2+(﹣0.7)+(﹣2.1)+0.8+3.5
(3)﹣3×2+(﹣2)2﹣5
(4)
(5)(﹣1)+(﹣6)+(﹣2)+
(6)25﹣3×[32+2×(﹣3)]+5.
(7)
(8)(﹣)×(﹣3)÷(﹣1)÷3
(9)
(10)
【考点】1G:有理数的混合运算.
【专题】511:实数;66:运算能力.
【分析】(1)原式利用减法法则变形,计算即可求出值;
(2)原式结合后,相加即可求出值;
(3)原式先计算乘方及乘法运算,再计算加减运算即可求出值;
(4)原式结合后,相加即可求出值;
(5)原式结合后,相加即可求出值;
(6)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可求出值;
(7)原式逆用乘法分配律计算即可求出值;
(8)原式从左到右依次计算即可求出值;
(9)原式先计算乘方运算,再计算乘除运算即可求出值;
(10)原式利用乘法分配律计算即可求出值.
【解答】解:(1)原式=﹣1+2﹣4=﹣3;
(2)原式=﹣0.8+0.8﹣0.7﹣2.1+1.2+3.5=1.9;
(3)原式=﹣6+4﹣5=﹣7;
(4)原式=1+﹣1﹣3﹣1=3﹣5﹣1=﹣3;
(5)原式=﹣1﹣2﹣6+=﹣4﹣3=﹣7;
(6)原式=25﹣3×(9﹣6)+5=25﹣9+5=21;
(7)原式=﹣×(3.2+6.8)=﹣×10=﹣3;
(8)原式=﹣×××=﹣;
(9)原式=﹣8××(﹣)=;
(10)原式=﹣32+12+18﹣10=﹣12.
21.如图,这是一个由小立方块塔成的几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请你画出它从正面和从左面看到的形状图.
【考点】U2:简单组合体的三视图;U4:作图﹣三视图.
【专题】55F:投影与视图.
【分析】由已知条件可知,主视图有3列,每列小正方形数目分别为3,2,4;左视图有3列,每列小正方形数目分别为2,3,4,据此可画出图形.
【解答】解:如图所示:
22.下表是某中学七年级5名学生的体重情况,试完成下表
姓名 小颖 小明 小刚 小京 小宁
体重(千克) 34 45
体重与平均体重的差 ﹣7 +3 ﹣4 0
(1)谁最重?谁最轻?
(2)最重的与最轻的相差多少?
【考点】18:有理数大小比较;1B:有理数的加减混合运算.
【专题】11:计算题.
【分析】(1)由小颖的体重与体重和平均体重的差,求出平均体重,进而确定出其他人的题中,填表后,找出最重的与最轻的即可;
(2)用最重的减去最轻的列出算式,计算即可得到结果.
【解答】解:(1)由小颖体重为34千克,体重与平均体重的差为﹣7,得到平均体重为34﹣(﹣7)=34+7=41(千克),
则小明的体重为41+3=44(千克);小刚的体重为44千克;小京的体重为41+(﹣4)=37(千克);小宁的体重为41千克,填表如下:
姓名 小颖 小明 小刚 小京 小宁
体重(千克) 34 44 45 37 41
体重与平均体重的差 ﹣7 +3 +4 ﹣4 0
∴小刚的体重最重;小颖的体重最轻;
(2)最重与最轻相差为45﹣34=11(千克).
23.有8箱橘子,以每箱15kg为标准,超过的千克数记为正数,不足的千克数记为负数,现记录如下(单位:千克):1.2,﹣0.8,2.3,1.7,﹣1.5,﹣2.7,2,﹣0.2,则这8箱橘子的总重量是多少?
【考点】11:正数和负数.
【分析】根据有理数的加法运算,可得答案.
【解答】1.2+(﹣0.8)+2.3+1.7+(﹣1.5)+(﹣2.7)+2+(﹣0.2)=1.2﹣0.8+2.3+1.7
﹣1.5﹣2.7+2﹣0.2
=(2.3+1.7+2)+(﹣0.8﹣2.7﹣1.5)+(1.2﹣0.2)
=6﹣5+1=2(kg).
则15×8+2=122(kg).
答:这8箱橘子的总重量是122千克.
24.某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶纪录如下(单位:千米):+10,﹣9,+7,﹣15,+6,﹣14,+4,﹣2
(1)A在岗亭何方?距岗亭多远?
(2)若摩托车行驶1千米耗油0.05升,这一天共耗油多少升?
【考点】11:正数和负数.
【分析】(1)根据有理数的加法运算,可得和,再根据和的大小,向北记为正,可判断位置;
(2)根据行车就耗油,可得总耗油量.
【解答】解:(1)10+(﹣9)+7+(﹣15)+6+(﹣14)+4+(﹣2)=﹣13,
答:A在岗亭南方,距岗亭13(千米);
(2)(10++7++6++4+)×0.05=3.35(升),
答:这一天共耗油3.35升.
25.如图是由棱长为1的小正方体堆砌成的几何体,
(1)画出这个几何体从正面、左面、上面看到的形状图;
(2)求堆砌成的几何体的表面积;
(3)求堆砌成的几何体的棱长.
【考点】I4:几何体的表面积;U4:作图﹣三视图.
【专题】55F:投影与视图;64:几何直观.
【分析】(1)直接利用三视图的画法进而得出答案;
(2)直接利用几何体的形状进而得出其表面;
(3)直接利用几何体的形状进而得出几何体的棱长.
【解答】解:(1)如图所示:
(2)堆砌成的几何体的表面积为:3+3+2+2+2+2=14;
(3)堆砌成的几何体的棱长为:22.
26.已知一个圆柱的侧面展开图为如图所示的矩形,它的一个底面圆的面积为多少?
【考点】I6:几何体的展开图.
【专题】55C:与圆有关的计算;64:几何直观.
【分析】分底面周长为4π和2π两种情况讨论,先求得底面半径,再根据圆的面积公式即可求解.
【解答】解:①底面周长为4π时,半径为4π÷π÷2=2,底面圆的面积为π×22=4π;
②底面周长为2π时,半径为2π÷π÷2=1,底面圆的面积为π×12=π.
故它的一个底面圆的面积为π或4π.
同课章节目录
