河北省承德市2018~2019学年高二第一学期(理)数学期末考试
文档属性
| 名称 | 河北省承德市2018~2019学年高二第一学期(理)数学期末考试 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 10:26:12 | ||
图片预览



文档简介
承德市2018~2019学年高二第一学期期末考试
数学试卷(理科)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的
1.命题“?x∈R,sinx>0”的否定是( )
A.?x∈R,sinx<0 B.?x∈R,sinx≤0
C.?x∈R,sinx≤0 D.?x∈R,sinx<0
2.在区间(0,1)上随机地取一个数a,则事件“2”发生的概率为( )
A. B. C. D.
3.已知样本数据x1,x2,…,xn的方差s2=2,则样本数据3x1+2,3x2+2,…,3xn+2的方差为( )
A.2 B.8 C.18 D.20
4.已知A={x|x>2m2﹣4},B={x|﹣2<x<6},若“x∈A”是“x∈B”的必要不充分条件,则实数m的取值范围是( )
A.﹣1<m<1 B.m C.﹣5≤m D.﹣1≤m≤1
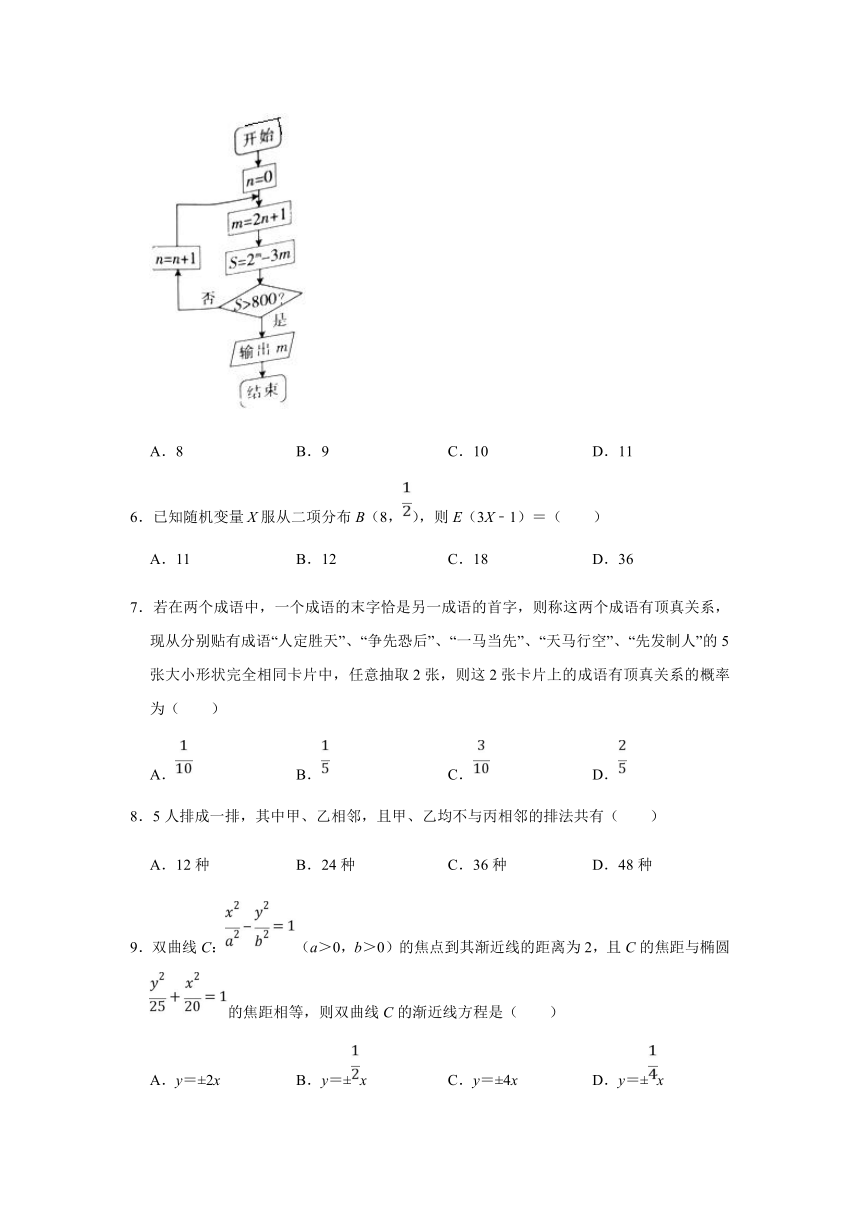
5.若执行如图所示的程序框图,则输出的m=( )
A.8 B.9 C.10 D.11
6.已知随机变量X服从二项分布B(8,),则E(3X﹣1)=( )
A.11 B.12 C.18 D.36
7.若在两个成语中,一个成语的末字恰是另一成语的首字,则称这两个成语有顶真关系,现从分别贴有成语“人定胜天”、“争先恐后”、“一马当先”、“天马行空”、“先发制人”的5张大小形状完全相同卡片中,任意抽取2张,则这2张卡片上的成语有顶真关系的概率为( )
A. B. C. D.
8.5人排成一排,其中甲、乙相邻,且甲、乙均不与丙相邻的排法共有( )
A.12种 B.24种 C.36种 D.48种
9.双曲线C:(a>0,b>0)的焦点到其渐近线的距离为2,且C的焦距与椭圆的焦距相等,则双曲线C的渐近线方程是( )
A.y=±2x B.y=±x C.y=±4x D.y=±x
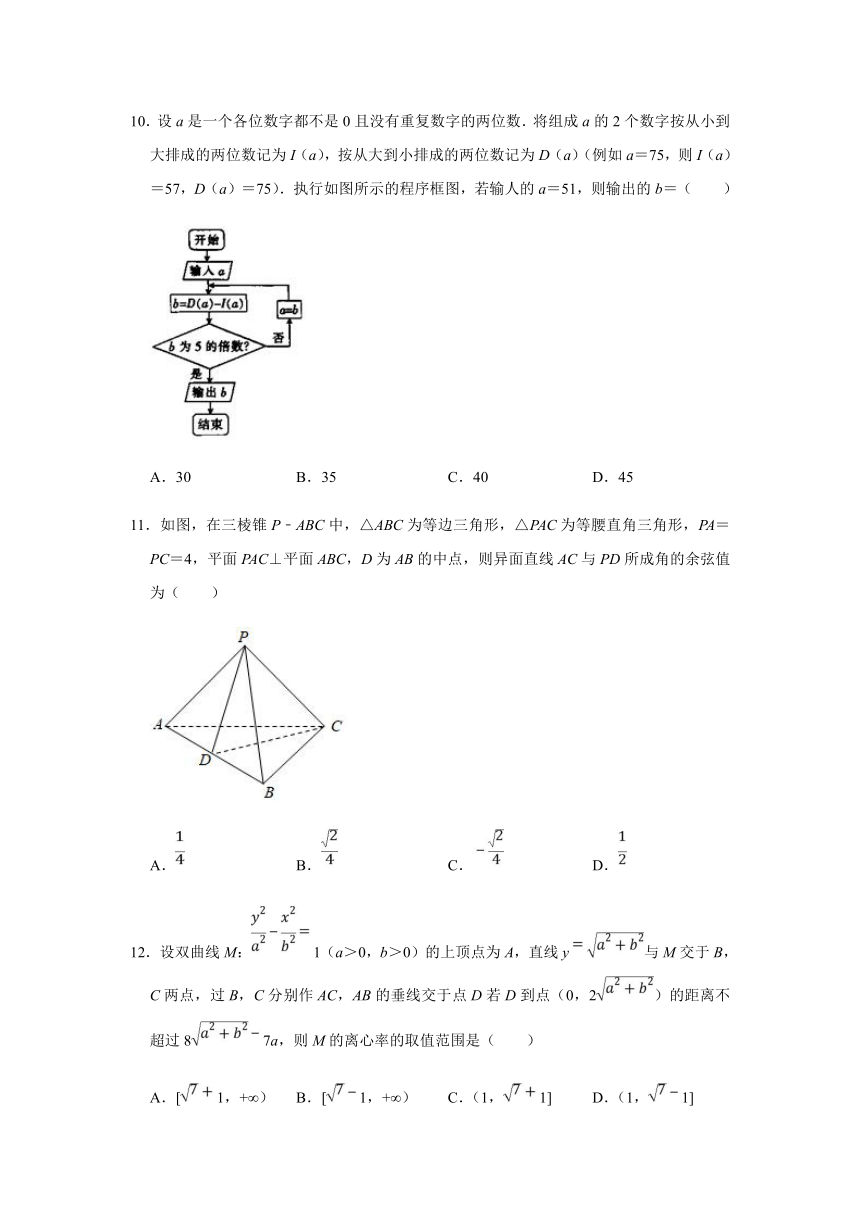
10.设a是一个各位数字都不是0且没有重复数字的两位数.将组成a的2个数字按从小到大排成的两位数记为I(a),按从大到小排成的两位数记为D(a)(例如a=75,则I(a)=57,D(a)=75).执行如图所示的程序框图,若输人的a=51,则输出的b=( )
A.30 B.35 C.40 D.45
11.如图,在三棱锥P﹣ABC中,△ABC为等边三角形,△PAC为等腰直角三角形,PA=PC=4,平面PAC⊥平面ABC,D为AB的中点,则异面直线AC与PD所成角的余弦值为( )
A. B. C. D.
12.设双曲线M:1(a>0,b>0)的上顶点为A,直线y与M交于B,C两点,过B,C分别作AC,AB的垂线交于点D若D到点(0,2)的距离不超过87a,则M的离心率的取值范围是( )
A.[1,+∞) B.[1,+∞) C.(1,1] D.(1,1]
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上
13.已知随机变量ξ服从正态分布N(4,σ2),若P(ξ<2)=0.3,则P(2<ξ<6)= .
14.(x)9的展开式中含x项的系数为 .(用数字作答)
15.已知直线l:2x﹣y﹣1=0与抛物线x2=﹣4y交于A,B两点,则|AB|= .
16.某同学进行投篮训练,在甲、乙、丙三个不同的位置投中的概率分别,,p,该同学站在这三个不同的位置各投篮一次,恰好投中两次的概率为,则p的值为 .
三、解答题:本大题共6小题共70分解答应写出文字说明、证明过程或演算步骤
17.己知p:函数f(x)在R上是增函数,f(m2)<f(m+2)成立;q:方程1(m∈R)表示双曲线.(1)若p为真命题,求m的取值范围;
(2)若p∨q为真,p∧q为假,求m的取值范围.
18.国家统计局对某市最近十年小麦的需求量进行统计调查发现小麦的需求量逐年上升,如表是部分统计数据:
年份x 2009 2011 2013 2015 2017
年需求量y(万吨) 336 346 357 376 385
(1)利用所给数据求年需求量y与年份x之间的回归直线方程x;
(2)请利用(1)中所求出的回归直线方程预测该市2019年的小麦需求量.
(参考公式:,)
19.某高校随机抽取部分男生测试立定跳远,将成绩整理得到频率分布表如表,测试成绩在220厘米以上(含220厘米)的男生定为“合格生”,成绩在260厘米以上(含260厘米)的男生定为“优良生”.
分组(厘米) 频数 频率
[180,200) 0.10
[200,220) 15
[220,240) 0.30
[240,260) 0.30
[260,280) 0.20
合计 1.00
(1)求参加测试的男生中“合格生”的人数.
(2)从参加测试的“合格生”中,根据表中分组情况,按分层抽样的方法抽取8名男生,再从这8名男生中抽取3名男生,记X表示3人中“优良生”的人数,求X的分布列及数学期望.
20.2016年1月1日,我国全面实行二孩政策,某机构进行了街头调查,在所有参与调查的青年男女中,持“响应”“犹豫”和“不响应”态度的人数如表所示:
响应 犹豫 不响应
男性青年 500 300 200
女性青年 300 200 300
(1)根据已知条件完成下面的2×2列联表,并判断能否有97.5%的把握认为犹豫与否与性别有关;
犹豫 不犹豫 总计
男性青年
女性青年
总计 1800
(2)以表中频率作为概率,若从街头随机采访青年男女各2人,求4人中“响应”的人数恰好是“不响应”的人数(“不响应”的人数不为0)的2倍的概率.
参考公式:
参考数据:
P(K2≥k0) 0.150 0.100 0.050 0.025 0.010
k0 2.072 2.706 3.841 5.024 6.635
21.在三棱锥P﹣ABC中,AB=1,BC=2,AC,PC,PA,PB,E是线段BC的中点.
(1)求点C到平面APE的距离d;
(2)求二面角P﹣EA﹣B的余弦值.
22.已知点P为椭圆C:1(a>b>0)上一点,F1,F2分别是椭圆C的左、右两个焦点,|PF1|=2|PF2|,且cos∠F1PF2,过点F2且斜率为k的直线l与椭圆C交于A,B两点.
(1)求椭圆C的离心率;
(2)若点M(1,)在C上,求△MAB面积的最大值.
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的
1.B
2.B
3C
4.D
5.D
6.A
7.C
8.B
9.A
10.D
11.B
12.D
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上
13.∵随机变量ξ服从正态分布N(4,σ2),∴其对称轴方程为x=μ=4,
又P(ξ<2)=0.3,∴P(ξ>6)=P(ξ<2)=0.3,
则P(2<ξ<6)=1﹣2×0.3=0.4.
14.(x)9展开式的通项公式为:
Tr+1?x9﹣r???x9﹣2r,
令9﹣2r=1,解得r=4;
所以展开式中含x项的系数为:
?126.
15.直线l:2x﹣y﹣1=0与抛物线x2=﹣4y联立,可得x2+8x﹣4=0,
设A(x1,y1),B(x2,y2),可得x1+x2=﹣8,x1x2=﹣4,
则|AB|??20.
16.在甲、乙、丙处投中分别记为事件A,B,C,
恰好投中两次为事件,,发生,
故恰好投中两次的概率:
P(1),
解得p.
三、解答题:本大题共6小题共70分解答应写出文字说明、证明过程或演算步骤
17.(1)己知命题p:函数f(x)在R上是增函数,f(m2)<f(m+2)成立;
所以m2<m+2,解得﹣1<m<2.
(2)已知命题q:方程1(m∈R)表示双曲线.
所以m(m﹣3)<0,解得0<m<3.
由于p∨q为真,p∧q为假,
所以①p真q假,则,解得﹣1<m≤0.
②p假q真,则,解得2≤m<3,
综上所述:m的取值范围是(﹣1,0]∪[2,3).
18.(1),.
.
.
∴所求线性回归方程为;
(2)在(1)中求得的线性回归方程中,取x=2019,
可得(万吨).
19.(1)第2小组的频率为:
1﹣(0.10+0.30+0.30+0.20)=0.10,
∴总人数为:150,
∴不是“合格生”的人数为:0.10×150+0.10×150=30.
∴参加测试的男生中“合格生”的人数为:
150﹣30=120.
(2)在“合格生”中根据分层抽样,有各组中抽取的人数分别为3人,3人,2人,
其中,“优良生”有2人,∴X的可能取值为0,1,2,
P(X=0),
P(X=1),
P(X=2),
∴X的分布列为:
X 0 1 3
P
EX.
20.(1)根据题意整理成2×2联表:
(1)根据已知条件完成下面的2×2列联表,并判断能否有97.5%的把握认为犹豫与否与性别有关;
犹豫 不犹豫 总计
男性青年 300 700 1000
女性青年 200 600 800
总计 500 1300 1800
所以5.538>5.024,
则有97.5%的把握认为犹豫与否与性别有关.
(2)男性青年中持“响应”“犹豫”“不响应”态度的概率为,,.
女性青年中持“响应”“犹豫”“不响应”态度的概率为,,.
因为选出的4人中“响应”的人数恰好是“不响应”人数的2倍.
所以响应的人数为2,不响应的人数为1,犹豫的人数为1,
所以所求的概率为P.
21.∵AB2+BC2=AC2,PC2+BC2=PB2,PA2+AB2=PB2,
∴,
过点P作PO⊥平面ABC,垂足为O,易得OP=1,且BC⊥OC,BA⊥OA,
∴四边形ABCO为矩形,
(1)以O为坐标原点,建立如图所示的空间直角坐标系,
则C(1,0,0),E(1,1,0),A(0,2,0),P(0,0,1),
,
设平面APE的法向量为,则,
令x=1,则,
∴;
(2)由(1)知平面APE的法向量为,取平面ABE的一个法向量,
且二面角P﹣EA﹣B为钝角,设其为θ,故.
22.(1)在△PF1F2中,设PF2=x,则PF1=2x,cos∠F1PF2,
由余弦定理得,(2c)2=x2+(2x)2﹣2?x?2x?cos∠F1PF2=5x2﹣4x2?,
∴xc,2xc,所以2a=x+2x=4c∴e,
所以椭圆的离心率为:.
(2)由(1)得:b2=a2﹣c2=3c2,椭圆的方程为:1,点M在椭圆上,1,
∴c2=1,b2=3,a2=4,
所以椭圆的方程为:1.右焦点(1,0),
设直线l的方程:y=k(x﹣1),A(x,y),B(x',y'),
当k=0时,|AB|=2a=4,M到l的距离为,S△MAB3,
当k≠0时,联立与椭圆的方程整理得:(3+4k2)x2﹣8k2x+4k2﹣12=0,x+x',xx',
弦长|AB||x﹣x'|12,
M在直线l的距离d,
所以S△MAB?|AB|?d=9993,
综上△MAB面积的最大值为:3.
