2020年湘教新版七年级上册数学《第4章 图形的认识》单元测试卷(解析版)
文档属性
| 名称 | 2020年湘教新版七年级上册数学《第4章 图形的认识》单元测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 319.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-05 00:00:00 | ||
图片预览




文档简介
2020年湘教新版七年级上册数学《第4章 图形的认识》单元测试卷
一.选择题(共10小题)
1.按组成面的平或曲划分,与圆柱为同一类的几何体是( )
A.长方体 B.正方体 C.棱柱 D.圆锥
2.如图绕虚线旋转得到的几何体是( )
A. B. C. D.
3.已知如图,则不含阴影部分的矩形的个数是( )
A.15 B.24 C.25 D.26
4.如图,共有线段( )
A.3条 B.4条 C.5条 D.6条
5.植树时,为了使同一行树坑在一条直线上,只需定出两个树坑的位置,其中的数学道理是( )
A.两点之间线段最短 B.两点之间直线最短
C.两点确定一条射线 D.两点确定一条直线
6.如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是( )
A.两点之间,直线最短 B.两点确定一条直线
C.两点之间,线段最短 D.经过一点有无数条直线
7.已知线段MN=10cm,点C是直线MN上一点,NC=4cm,若P是线段MN的中点,Q是线段NC的中点,则线段PQ的长度是( )
A.7cm B.7cm或3cm C.5cm D.3cm
8.如图AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD C.AC=BD D.无法确定
9.能用∠α、∠AOB、∠O三种方式表示同一个角的图形是( )
A. B.
C. D.
10.钟表4点30分时,时针与分针所成的角的度数为( )
A.45° B.30° C.60° D.75°
二.填空题(共8小题)
11.圆锥由 个面围成,其中 个平面, 个曲面.
12.“枪打一条线,棍打一大片”这个现象说明: .
13.观察下列图形的排列规律(其中△是三角形,□是正方形,〇是圆),〇△□□〇△□〇△□□〇△□……若第一个图形是圆,则第2008个图形是 (填图形名称).
14.表反映了平面内直线条数与它们最多交点个数的对应关系:
图形 …
直线条数 2 3 4 …
最多交点个数 1 3=1+2 6=1+2+3 …
按此规律,6条直线相交,最多有 个交点;n条直线相交,最多有 个交点.(n为正整数)
15.建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是: .
16.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是 .
17.已知C、D是线段AB上的两点,点C是AD的中点,AB=10cm,AC=4cm,则DB的长度为 cm.
18.如图,若CB=4cm,DB=7cm,且D是AC的中点,则AC= cm.
三.解答题(共8小题)
19.(1)下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称.
( ) ( ) ( ) ( ) ( )
(2)将这些几何体分类,并写出分类的理由.
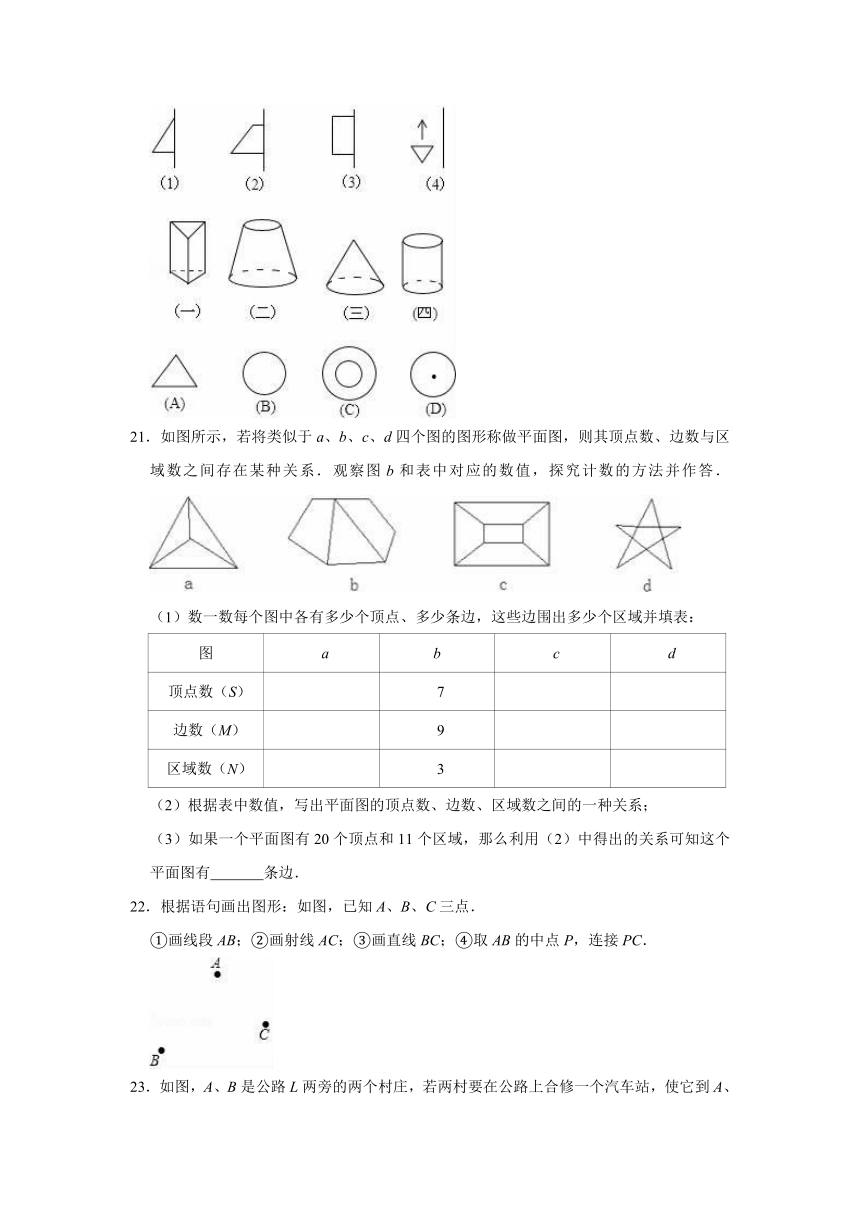
20.用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.
21.如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.
(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
图 a b c d
顶点数(S) 7
边数(M) 9
区域数(N) 3
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有 条边.
22.根据语句画出图形:如图,已知A、B、C三点.
①画线段AB;②画射线AC;③画直线BC;④取AB的中点P,连接PC.
23.如图,A、B是公路L两旁的两个村庄,若两村要在公路上合修一个汽车站,使它到A、B两村的距离和最小,试在L上标注出点P的位置,并说明理由.
24.如图,线段AB=8,M是线段AB的中点,N是线段AC的中点,C为线段AB上一点,且AC=3.2,求M,N两点间的距离.
25.已知线段a、b,作线段AB=a+b(要求:保留作图痕迹).
26.根据条件画出图形,并回答问题
(1)三条直线a、b、c,直线a、c相交于点B,直线b、c相交于点A,直线a、b相交于点C,点D在线段AC上,点E在线段DC上.则DE= ﹣ ﹣ ;
(2)画任意∠AOB,使∠AOB<180°,在∠AOB内部再任意作两条射线OC、OD,则图中共有 个角.
2020年湘教新版七年级上册数学《第4章 图形的认识》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.按组成面的平或曲划分,与圆柱为同一类的几何体是( )
A.长方体 B.正方体 C.棱柱 D.圆锥
【分析】分别写出四个选项中的几何体是由什么面组成可直接选出答案.
【解答】解:圆柱由平面和曲面组成,
长方体由平面组成;正方体由平面组成;棱柱由平面组成,圆锥由平面和曲面组成,
故选:D.
【点评】此题主要考查了认识立体图形,关键是正确认识曲面和平面.
2.如图绕虚线旋转得到的几何体是( )
A. B. C. D.
【分析】根据面旋转成体的原理及日常生活中的常识解题即可.
【解答】解:根据旋转及线动成面的知识可得旋转后的图形为:两边为圆锥,中间为圆柱.
故选:D.
【点评】本题考查线动成面的知识,属于基础题,注意掌握线动成面的概念.
3.已知如图,则不含阴影部分的矩形的个数是( )
A.15 B.24 C.25 D.26
【分析】图形中不含阴影的最小的矩形有10个,两个小矩形组成的矩形有10个,三个小矩形组成的矩形有4个,四个小矩形组成的矩形有2个.
【解答】解:根据以上分析不含阴影的矩形个数为26个.
故选:D.
【点评】本题可分类找出图形中的矩形,这样可以不重不漏.
4.如图,共有线段( )
A.3条 B.4条 C.5条 D.6条
【分析】根据在一直线上有n点,一共能组成线段的条数的公式:,代入可直接选出答案.
【解答】解:线段AB、AC、AD、BC、BD、CD共六条,也可以根据公式计算,=6,故选D.
【点评】在线段的计数时,应注重分类讨论的方法计数,做到不遗漏,不重复.
5.植树时,为了使同一行树坑在一条直线上,只需定出两个树坑的位置,其中的数学道理是( )
A.两点之间线段最短 B.两点之间直线最短
C.两点确定一条射线 D.两点确定一条直线
【分析】根据公理“两点确定一条直线”来解答即可.
【解答】解:只要定出两个树坑的位置,这条直线就确定了,即两点确定一条直线.
故选:D.
【点评】本题考查的是“两点确定一条直线”在实际生活中的运用,此类题目有利于培养学生生活联系实际的能力.
6.如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是( )
A.两点之间,直线最短 B.两点确定一条直线
C.两点之间,线段最短 D.经过一点有无数条直线
【分析】根据线段的性质,可得答案.
【解答】解:由于两点之间线段最短,
∴剩下树叶的周长比原树叶的周长小,
故选:C.
【点评】本题考查了线段的性质,利用线段的性质是解题关键.
7.已知线段MN=10cm,点C是直线MN上一点,NC=4cm,若P是线段MN的中点,Q是线段NC的中点,则线段PQ的长度是( )
A.7cm B.7cm或3cm C.5cm D.3cm
【分析】根据线段中点的性质,可得PN,QN,根据线段的和差,可得答案.
【解答】解:P是线段MN的中点,Q是线段NC的中点,得
PN=MN=×10=5cm,QN=NC=×4=2cm.
①当C在MN上时,如图1,
PQ=PN﹣QN=5﹣2=3cm;
②当C在MN的延长线上时如图2,
PQ=PN+QN=5+2=7cmm,
③点C在MN的反向延长线上,NC<MN,不成立,
故选:B.
【点评】本题考查了两点间的距离,分类讨论是解题关键,以防遗漏.
8.如图AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD C.AC=BD D.无法确定
【分析】根据AB=CD两边都加上线段BC得出AB+BC=CD+BC,即可得出答案.
【解答】解:∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
故选:C.
【点评】本题考查了比较线段的长度的应用,主要考查学生的推理能力.
9.能用∠α、∠AOB、∠O三种方式表示同一个角的图形是( )
A. B.
C. D.
【分析】根据角的表示方法进行逐一分析,即角可以用一个大写字母表示,也可以用三个大写字母表示.其中顶点字母要写在中间,唯有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角.角还可以用一个希腊字母(如∠α,∠β,∠γ、…)表示,或用阿拉伯数字(∠1,∠2…)表示.
【解答】解:A、因为顶点O处有四个角,所以这四个角均不能用∠O表示,故本选项错误;
B、因为顶点O处只有一个角,所以这个角能用∠O、∠α及∠AOB表示,故本选项正确;
C、因为顶点O处有三个角,所以这三个角均不能用∠O表示,故本选项错误;
D、因为∠O与∠α表示的不是同一个角,故本选项错误.
故选:B.
【点评】本题考查的是角的表示方法,熟知角的三种表示方法是解答此题的关键.
10.钟表4点30分时,时针与分针所成的角的度数为( )
A.45° B.30° C.60° D.75°
【分析】本题考查了钟表里的旋转角的问题,钟表表盘被分成12大格,每一大格又被分为5小格,故表盘共被分成60小格,每一小格所对角的度数为6°.分针转动一圈,时间为60分钟,则时针转1大格,即时针转动30°.也就是说,分针转动360°时,时针才转动30°,即分针每转动1°,时针才转动()度,逆过来同理.
【解答】解:∵4点30分时,时针指向4与5之间,分针指向6,钟表12个数字,每相邻两个数字之间的夹角为30°,
∴4点30分时分针与时针的夹角是2×30°﹣15°=45度.
故选:A.
【点评】本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每转动1°时针转动()°,并且利用起点时间时针和分针的位置关系建立角的图形.
二.填空题(共8小题)
11.圆锥由 2 个面围成,其中 1 个平面, 1 个曲面.
【分析】根据圆锥的概念和特性即可解.
【解答】解:圆锥的侧面为曲面,底面为平面.
∴圆锥由2个面围成,其中1个平面,1个曲面.
故答案为2,1,1.
【点评】本题主要考查圆锥的构造特征:由一个平面和一个曲面组成.
12.“枪打一条线,棍打一大片”这个现象说明: 点动成线,线动成面 .
【分析】子弹可看作一个点,棍可看作一条线,由此可得出这个现象的本质.
【解答】解:子弹可看作一个点,棍可看作一条线,
∴“枪打一条线,棍打一大片”这个现象说明:点动成线,线动成面.
故答案为:点动成线,线动成面.
【点评】本题考查点、线、面得关系,难度不大,注意将生活中的实物抽象为数学上的模型.
13.观察下列图形的排列规律(其中△是三角形,□是正方形,〇是圆),〇△□□〇△□〇△□□〇△□……若第一个图形是圆,则第2008个图形是 三角形 (填图形名称).
【分析】解此类题首先要仔细观察图形找出其中的规律进行解答.
【解答】解:观察图形的排列规律知,7个图形循环一次,2008÷7=286…6,又由第一个图形是圆形,则第2008个图形是三角形.
故答案为:三角形.
【点评】本题属于总结规律的问题,注意观察所给出的图形的排列特点,主要看它的循环规律.
14.表反映了平面内直线条数与它们最多交点个数的对应关系:
图形 …
直线条数 2 3 4 …
最多交点个数 1 3=1+2 6=1+2+3 …
按此规律,6条直线相交,最多有 15 个交点;n条直线相交,最多有 个交点.(n为正整数)
【分析】根据观察,可发现规律:n条直线最多的交点是1+2+3+…+(n﹣1),可得答案.
【解答】解:6条直线相交,最多有个交点1+2+3+4+5=15;
n条直线相交,最多有个交点,
故答案为:15,.
【点评】本题考查了直线,每两条直线有一个交点得出n条直线最多的交点是1+2+3+…+(n﹣1)是解题关键
15.建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是: 两点确定一条直线 .
【分析】由直线公理可直接得出答案.
【解答】解:建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.
故答案为:两点确定一条直线.
【点评】本题主要考查的是直线的性质,掌握直线的性质是解题的关键.
16.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是 两点之间线段最短 .
【分析】直接利用线段的性质进而分析得出答案.
【解答】解:田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,
能正确解释这一现象的数学知识是:两点之间线段最短.
故答案为:两点之间线段最短.
【点评】此题主要考查了线段的性质,正确把握线段的性质是解题关键.
17.已知C、D是线段AB上的两点,点C是AD的中点,AB=10cm,AC=4cm,则DB的长度为 2 cm.
【分析】根据线段中点的性质,可得AD的长,再根据线段的和差,可得答案.
【解答】解:由点C是AD的中点,AC=4cm,得
AD=2AC=8cm.
由线段的和差,得
DB=AB﹣AD=10﹣8=2cm,
故答案为:2.
【点评】本题考查了两点间的距离,利用线段中点的性质得出AD的长是解题关键.
18.如图,若CB=4cm,DB=7cm,且D是AC的中点,则AC= 6 cm.
【分析】理解线段的中点这一概念,灵活运用线段的和、差、倍、分转化线段之间的数量关系进行解题.
【解答】解:CD=DB﹣BC=7﹣4=3cm,
AC=2CD=2×3=6cm.
故答案为:6.
【点评】灵活运用线段的和、差、倍、分转化线段之间的数量关系是十分关键的一点.
三.解答题(共8小题)
19.(1)下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称.
( ) ( ) ( ) ( ) ( )
(2)将这些几何体分类,并写出分类的理由.
【分析】(1)针对立体图形的特征,直接填写它们的名称即可.
(2)可以按柱体、锥体和球进行分类,也可以按平面和曲面进行分类,方法不同,答案不同,只要合理即可.
【解答】解:(1)从左向右依次是:球、圆柱、圆锥、长方体、三棱柱.
(2)观察图形,按柱、锥、球划分,则有圆柱、长方体、三棱柱为柱体;圆锥为锥体;球为球体.
【点评】本题考查了立体图形的认识和几何体的分类.熟记常见立体图形的特征是解决此类问题的关键.几何体的分类,从图形形状可以分为柱体、锥体和球三种,注意结合实际几何体的特征进行分类.
20.用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.
【分析】本题是一个平面围绕一条边为对称轴旋转一周根据面动成体的原理.可知形成的立体图形以及与俯视图间的关联.
【解答】解:从第一行的平面图形绕某一边旋转可得到第二行的立体图形,从第二行的立体图形的上面看可得到第三行的平面图形.
(1)→(三)→(D);
(2)→(二)→(C);
(3)→(四)→(B);
(4)→(一)→(A).
【点评】本题考查了平面图形和立体图形的联系,长方形绕一边旋转一周,得到的几何体是圆柱,一个三角形绕一边旋转一周,得到的几何体是圆锥.
21.如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.
(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
图 a b c d
顶点数(S) 7
边数(M) 9
区域数(N) 3
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有 30 条边.
【分析】(1)按照自己熟悉的规律去数顶点数,边数以及区域数;
(2)4+3﹣6=1,7+3﹣9=1,8+5﹣12=1,10+6﹣15=1,所以可得到一般规律:顶点数+区域数一边数=1;
(3)边数=顶点数+区域数﹣1.
【解答】解:(1)
图 a b c d
顶点数(S) 4 7 8 10
边数(M) 6 9 12 15
区域数(N) 3 3 5 6
(2)观察表中数据可得;4+3﹣6=1,7+3﹣9=1,8+5﹣12=1,10+6﹣15=1
∴S+N﹣M=1;(或顶点数+区域数一边数=1)
(3)由(2)得:边数=顶点数+区域数﹣1=20+11﹣1=30.
【点评】本题考查学生的观察能力,分析以及合理推理能力.注意应按平面图来进行解答.
22.根据语句画出图形:如图,已知A、B、C三点.
①画线段AB;②画射线AC;③画直线BC;④取AB的中点P,连接PC.
【分析】根据直线、线段、射线的画法,可得答案.
【解答】解:如图.
【点评】本题考查了直线、射线、线段,正确区分直线、线段、射线是解题关键.
23.如图,A、B是公路L两旁的两个村庄,若两村要在公路上合修一个汽车站,使它到A、B两村的距离和最小,试在L上标注出点P的位置,并说明理由.
【分析】根据线段的性质:两点之间线段最短,即可得出答案.
【解答】解:点P的位置如下图所示:
作法是:连接AB交L于点P,则P点为汽车站位置,
理由是:两点之间,线段最短.
【点评】本题考查了线段的性质,属于基础题,注意两点之间线段最短这一知识点的灵活运用.
24.如图,线段AB=8,M是线段AB的中点,N是线段AC的中点,C为线段AB上一点,且AC=3.2,求M,N两点间的距离.
【分析】根据线段的中点定义求出AN和AM,相减即可求出答案.
【解答】解:∵M是AB的中点,AB=8,
∴AM=AB=4,
∵AC=3.2,N是AC的中点,
∴AN=AC=1.6,
∴MN=AM﹣AN=4﹣1.6=2.4cm.
【点评】本题考查了两点间的距离和线段中点的定义,关键是求出AN和AM的长,题目比较典型,难度不大.
25.已知线段a、b,作线段AB=a+b(要求:保留作图痕迹).
【分析】可先作一条线段等于已知线段a,进而在所作的线段的延长线上再作一条线段等于b即可.
【解答】解:作图:
①作线段AC=a;
②在线段AC的延长线上作BC=b.
线段AB就是所求的线段.
【点评】本题考查两条线段的和的画法,注意第二条线段应在第一条线段的延长线上.
26.根据条件画出图形,并回答问题
(1)三条直线a、b、c,直线a、c相交于点B,直线b、c相交于点A,直线a、b相交于点C,点D在线段AC上,点E在线段DC上.则DE= AC ﹣ AD ﹣ EC ;
(2)画任意∠AOB,使∠AOB<180°,在∠AOB内部再任意作两条射线OC、OD,则图中共有 6 个角.
【分析】根据题意,正确画出图形,结合图形求解即可.
【解答】解:(1)DE=AC﹣AD﹣EC;
(2)6个.
【点评】考查直线、线段、射线及角的概念.解题的关键是正确画出图形,注意图形结合的解题思想.
一.选择题(共10小题)
1.按组成面的平或曲划分,与圆柱为同一类的几何体是( )
A.长方体 B.正方体 C.棱柱 D.圆锥
2.如图绕虚线旋转得到的几何体是( )
A. B. C. D.
3.已知如图,则不含阴影部分的矩形的个数是( )
A.15 B.24 C.25 D.26
4.如图,共有线段( )
A.3条 B.4条 C.5条 D.6条
5.植树时,为了使同一行树坑在一条直线上,只需定出两个树坑的位置,其中的数学道理是( )
A.两点之间线段最短 B.两点之间直线最短
C.两点确定一条射线 D.两点确定一条直线
6.如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是( )
A.两点之间,直线最短 B.两点确定一条直线
C.两点之间,线段最短 D.经过一点有无数条直线
7.已知线段MN=10cm,点C是直线MN上一点,NC=4cm,若P是线段MN的中点,Q是线段NC的中点,则线段PQ的长度是( )
A.7cm B.7cm或3cm C.5cm D.3cm
8.如图AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD C.AC=BD D.无法确定
9.能用∠α、∠AOB、∠O三种方式表示同一个角的图形是( )
A. B.
C. D.
10.钟表4点30分时,时针与分针所成的角的度数为( )
A.45° B.30° C.60° D.75°
二.填空题(共8小题)
11.圆锥由 个面围成,其中 个平面, 个曲面.
12.“枪打一条线,棍打一大片”这个现象说明: .
13.观察下列图形的排列规律(其中△是三角形,□是正方形,〇是圆),〇△□□〇△□〇△□□〇△□……若第一个图形是圆,则第2008个图形是 (填图形名称).
14.表反映了平面内直线条数与它们最多交点个数的对应关系:
图形 …
直线条数 2 3 4 …
最多交点个数 1 3=1+2 6=1+2+3 …
按此规律,6条直线相交,最多有 个交点;n条直线相交,最多有 个交点.(n为正整数)
15.建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是: .
16.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是 .
17.已知C、D是线段AB上的两点,点C是AD的中点,AB=10cm,AC=4cm,则DB的长度为 cm.
18.如图,若CB=4cm,DB=7cm,且D是AC的中点,则AC= cm.
三.解答题(共8小题)
19.(1)下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称.
( ) ( ) ( ) ( ) ( )
(2)将这些几何体分类,并写出分类的理由.
20.用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.
21.如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.
(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
图 a b c d
顶点数(S) 7
边数(M) 9
区域数(N) 3
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有 条边.
22.根据语句画出图形:如图,已知A、B、C三点.
①画线段AB;②画射线AC;③画直线BC;④取AB的中点P,连接PC.
23.如图,A、B是公路L两旁的两个村庄,若两村要在公路上合修一个汽车站,使它到A、B两村的距离和最小,试在L上标注出点P的位置,并说明理由.
24.如图,线段AB=8,M是线段AB的中点,N是线段AC的中点,C为线段AB上一点,且AC=3.2,求M,N两点间的距离.
25.已知线段a、b,作线段AB=a+b(要求:保留作图痕迹).
26.根据条件画出图形,并回答问题
(1)三条直线a、b、c,直线a、c相交于点B,直线b、c相交于点A,直线a、b相交于点C,点D在线段AC上,点E在线段DC上.则DE= ﹣ ﹣ ;
(2)画任意∠AOB,使∠AOB<180°,在∠AOB内部再任意作两条射线OC、OD,则图中共有 个角.
2020年湘教新版七年级上册数学《第4章 图形的认识》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.按组成面的平或曲划分,与圆柱为同一类的几何体是( )
A.长方体 B.正方体 C.棱柱 D.圆锥
【分析】分别写出四个选项中的几何体是由什么面组成可直接选出答案.
【解答】解:圆柱由平面和曲面组成,
长方体由平面组成;正方体由平面组成;棱柱由平面组成,圆锥由平面和曲面组成,
故选:D.
【点评】此题主要考查了认识立体图形,关键是正确认识曲面和平面.
2.如图绕虚线旋转得到的几何体是( )
A. B. C. D.
【分析】根据面旋转成体的原理及日常生活中的常识解题即可.
【解答】解:根据旋转及线动成面的知识可得旋转后的图形为:两边为圆锥,中间为圆柱.
故选:D.
【点评】本题考查线动成面的知识,属于基础题,注意掌握线动成面的概念.
3.已知如图,则不含阴影部分的矩形的个数是( )
A.15 B.24 C.25 D.26
【分析】图形中不含阴影的最小的矩形有10个,两个小矩形组成的矩形有10个,三个小矩形组成的矩形有4个,四个小矩形组成的矩形有2个.
【解答】解:根据以上分析不含阴影的矩形个数为26个.
故选:D.
【点评】本题可分类找出图形中的矩形,这样可以不重不漏.
4.如图,共有线段( )
A.3条 B.4条 C.5条 D.6条
【分析】根据在一直线上有n点,一共能组成线段的条数的公式:,代入可直接选出答案.
【解答】解:线段AB、AC、AD、BC、BD、CD共六条,也可以根据公式计算,=6,故选D.
【点评】在线段的计数时,应注重分类讨论的方法计数,做到不遗漏,不重复.
5.植树时,为了使同一行树坑在一条直线上,只需定出两个树坑的位置,其中的数学道理是( )
A.两点之间线段最短 B.两点之间直线最短
C.两点确定一条射线 D.两点确定一条直线
【分析】根据公理“两点确定一条直线”来解答即可.
【解答】解:只要定出两个树坑的位置,这条直线就确定了,即两点确定一条直线.
故选:D.
【点评】本题考查的是“两点确定一条直线”在实际生活中的运用,此类题目有利于培养学生生活联系实际的能力.
6.如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是( )
A.两点之间,直线最短 B.两点确定一条直线
C.两点之间,线段最短 D.经过一点有无数条直线
【分析】根据线段的性质,可得答案.
【解答】解:由于两点之间线段最短,
∴剩下树叶的周长比原树叶的周长小,
故选:C.
【点评】本题考查了线段的性质,利用线段的性质是解题关键.
7.已知线段MN=10cm,点C是直线MN上一点,NC=4cm,若P是线段MN的中点,Q是线段NC的中点,则线段PQ的长度是( )
A.7cm B.7cm或3cm C.5cm D.3cm
【分析】根据线段中点的性质,可得PN,QN,根据线段的和差,可得答案.
【解答】解:P是线段MN的中点,Q是线段NC的中点,得
PN=MN=×10=5cm,QN=NC=×4=2cm.
①当C在MN上时,如图1,
PQ=PN﹣QN=5﹣2=3cm;
②当C在MN的延长线上时如图2,
PQ=PN+QN=5+2=7cmm,
③点C在MN的反向延长线上,NC<MN,不成立,
故选:B.
【点评】本题考查了两点间的距离,分类讨论是解题关键,以防遗漏.
8.如图AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD C.AC=BD D.无法确定
【分析】根据AB=CD两边都加上线段BC得出AB+BC=CD+BC,即可得出答案.
【解答】解:∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
故选:C.
【点评】本题考查了比较线段的长度的应用,主要考查学生的推理能力.
9.能用∠α、∠AOB、∠O三种方式表示同一个角的图形是( )
A. B.
C. D.
【分析】根据角的表示方法进行逐一分析,即角可以用一个大写字母表示,也可以用三个大写字母表示.其中顶点字母要写在中间,唯有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角.角还可以用一个希腊字母(如∠α,∠β,∠γ、…)表示,或用阿拉伯数字(∠1,∠2…)表示.
【解答】解:A、因为顶点O处有四个角,所以这四个角均不能用∠O表示,故本选项错误;
B、因为顶点O处只有一个角,所以这个角能用∠O、∠α及∠AOB表示,故本选项正确;
C、因为顶点O处有三个角,所以这三个角均不能用∠O表示,故本选项错误;
D、因为∠O与∠α表示的不是同一个角,故本选项错误.
故选:B.
【点评】本题考查的是角的表示方法,熟知角的三种表示方法是解答此题的关键.
10.钟表4点30分时,时针与分针所成的角的度数为( )
A.45° B.30° C.60° D.75°
【分析】本题考查了钟表里的旋转角的问题,钟表表盘被分成12大格,每一大格又被分为5小格,故表盘共被分成60小格,每一小格所对角的度数为6°.分针转动一圈,时间为60分钟,则时针转1大格,即时针转动30°.也就是说,分针转动360°时,时针才转动30°,即分针每转动1°,时针才转动()度,逆过来同理.
【解答】解:∵4点30分时,时针指向4与5之间,分针指向6,钟表12个数字,每相邻两个数字之间的夹角为30°,
∴4点30分时分针与时针的夹角是2×30°﹣15°=45度.
故选:A.
【点评】本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每转动1°时针转动()°,并且利用起点时间时针和分针的位置关系建立角的图形.
二.填空题(共8小题)
11.圆锥由 2 个面围成,其中 1 个平面, 1 个曲面.
【分析】根据圆锥的概念和特性即可解.
【解答】解:圆锥的侧面为曲面,底面为平面.
∴圆锥由2个面围成,其中1个平面,1个曲面.
故答案为2,1,1.
【点评】本题主要考查圆锥的构造特征:由一个平面和一个曲面组成.
12.“枪打一条线,棍打一大片”这个现象说明: 点动成线,线动成面 .
【分析】子弹可看作一个点,棍可看作一条线,由此可得出这个现象的本质.
【解答】解:子弹可看作一个点,棍可看作一条线,
∴“枪打一条线,棍打一大片”这个现象说明:点动成线,线动成面.
故答案为:点动成线,线动成面.
【点评】本题考查点、线、面得关系,难度不大,注意将生活中的实物抽象为数学上的模型.
13.观察下列图形的排列规律(其中△是三角形,□是正方形,〇是圆),〇△□□〇△□〇△□□〇△□……若第一个图形是圆,则第2008个图形是 三角形 (填图形名称).
【分析】解此类题首先要仔细观察图形找出其中的规律进行解答.
【解答】解:观察图形的排列规律知,7个图形循环一次,2008÷7=286…6,又由第一个图形是圆形,则第2008个图形是三角形.
故答案为:三角形.
【点评】本题属于总结规律的问题,注意观察所给出的图形的排列特点,主要看它的循环规律.
14.表反映了平面内直线条数与它们最多交点个数的对应关系:
图形 …
直线条数 2 3 4 …
最多交点个数 1 3=1+2 6=1+2+3 …
按此规律,6条直线相交,最多有 15 个交点;n条直线相交,最多有 个交点.(n为正整数)
【分析】根据观察,可发现规律:n条直线最多的交点是1+2+3+…+(n﹣1),可得答案.
【解答】解:6条直线相交,最多有个交点1+2+3+4+5=15;
n条直线相交,最多有个交点,
故答案为:15,.
【点评】本题考查了直线,每两条直线有一个交点得出n条直线最多的交点是1+2+3+…+(n﹣1)是解题关键
15.建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是: 两点确定一条直线 .
【分析】由直线公理可直接得出答案.
【解答】解:建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.
故答案为:两点确定一条直线.
【点评】本题主要考查的是直线的性质,掌握直线的性质是解题的关键.
16.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是 两点之间线段最短 .
【分析】直接利用线段的性质进而分析得出答案.
【解答】解:田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,
能正确解释这一现象的数学知识是:两点之间线段最短.
故答案为:两点之间线段最短.
【点评】此题主要考查了线段的性质,正确把握线段的性质是解题关键.
17.已知C、D是线段AB上的两点,点C是AD的中点,AB=10cm,AC=4cm,则DB的长度为 2 cm.
【分析】根据线段中点的性质,可得AD的长,再根据线段的和差,可得答案.
【解答】解:由点C是AD的中点,AC=4cm,得
AD=2AC=8cm.
由线段的和差,得
DB=AB﹣AD=10﹣8=2cm,
故答案为:2.
【点评】本题考查了两点间的距离,利用线段中点的性质得出AD的长是解题关键.
18.如图,若CB=4cm,DB=7cm,且D是AC的中点,则AC= 6 cm.
【分析】理解线段的中点这一概念,灵活运用线段的和、差、倍、分转化线段之间的数量关系进行解题.
【解答】解:CD=DB﹣BC=7﹣4=3cm,
AC=2CD=2×3=6cm.
故答案为:6.
【点评】灵活运用线段的和、差、倍、分转化线段之间的数量关系是十分关键的一点.
三.解答题(共8小题)
19.(1)下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称.
( ) ( ) ( ) ( ) ( )
(2)将这些几何体分类,并写出分类的理由.
【分析】(1)针对立体图形的特征,直接填写它们的名称即可.
(2)可以按柱体、锥体和球进行分类,也可以按平面和曲面进行分类,方法不同,答案不同,只要合理即可.
【解答】解:(1)从左向右依次是:球、圆柱、圆锥、长方体、三棱柱.
(2)观察图形,按柱、锥、球划分,则有圆柱、长方体、三棱柱为柱体;圆锥为锥体;球为球体.
【点评】本题考查了立体图形的认识和几何体的分类.熟记常见立体图形的特征是解决此类问题的关键.几何体的分类,从图形形状可以分为柱体、锥体和球三种,注意结合实际几何体的特征进行分类.
20.用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.
【分析】本题是一个平面围绕一条边为对称轴旋转一周根据面动成体的原理.可知形成的立体图形以及与俯视图间的关联.
【解答】解:从第一行的平面图形绕某一边旋转可得到第二行的立体图形,从第二行的立体图形的上面看可得到第三行的平面图形.
(1)→(三)→(D);
(2)→(二)→(C);
(3)→(四)→(B);
(4)→(一)→(A).
【点评】本题考查了平面图形和立体图形的联系,长方形绕一边旋转一周,得到的几何体是圆柱,一个三角形绕一边旋转一周,得到的几何体是圆锥.
21.如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.
(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
图 a b c d
顶点数(S) 7
边数(M) 9
区域数(N) 3
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有 30 条边.
【分析】(1)按照自己熟悉的规律去数顶点数,边数以及区域数;
(2)4+3﹣6=1,7+3﹣9=1,8+5﹣12=1,10+6﹣15=1,所以可得到一般规律:顶点数+区域数一边数=1;
(3)边数=顶点数+区域数﹣1.
【解答】解:(1)
图 a b c d
顶点数(S) 4 7 8 10
边数(M) 6 9 12 15
区域数(N) 3 3 5 6
(2)观察表中数据可得;4+3﹣6=1,7+3﹣9=1,8+5﹣12=1,10+6﹣15=1
∴S+N﹣M=1;(或顶点数+区域数一边数=1)
(3)由(2)得:边数=顶点数+区域数﹣1=20+11﹣1=30.
【点评】本题考查学生的观察能力,分析以及合理推理能力.注意应按平面图来进行解答.
22.根据语句画出图形:如图,已知A、B、C三点.
①画线段AB;②画射线AC;③画直线BC;④取AB的中点P,连接PC.
【分析】根据直线、线段、射线的画法,可得答案.
【解答】解:如图.
【点评】本题考查了直线、射线、线段,正确区分直线、线段、射线是解题关键.
23.如图,A、B是公路L两旁的两个村庄,若两村要在公路上合修一个汽车站,使它到A、B两村的距离和最小,试在L上标注出点P的位置,并说明理由.
【分析】根据线段的性质:两点之间线段最短,即可得出答案.
【解答】解:点P的位置如下图所示:
作法是:连接AB交L于点P,则P点为汽车站位置,
理由是:两点之间,线段最短.
【点评】本题考查了线段的性质,属于基础题,注意两点之间线段最短这一知识点的灵活运用.
24.如图,线段AB=8,M是线段AB的中点,N是线段AC的中点,C为线段AB上一点,且AC=3.2,求M,N两点间的距离.
【分析】根据线段的中点定义求出AN和AM,相减即可求出答案.
【解答】解:∵M是AB的中点,AB=8,
∴AM=AB=4,
∵AC=3.2,N是AC的中点,
∴AN=AC=1.6,
∴MN=AM﹣AN=4﹣1.6=2.4cm.
【点评】本题考查了两点间的距离和线段中点的定义,关键是求出AN和AM的长,题目比较典型,难度不大.
25.已知线段a、b,作线段AB=a+b(要求:保留作图痕迹).
【分析】可先作一条线段等于已知线段a,进而在所作的线段的延长线上再作一条线段等于b即可.
【解答】解:作图:
①作线段AC=a;
②在线段AC的延长线上作BC=b.
线段AB就是所求的线段.
【点评】本题考查两条线段的和的画法,注意第二条线段应在第一条线段的延长线上.
26.根据条件画出图形,并回答问题
(1)三条直线a、b、c,直线a、c相交于点B,直线b、c相交于点A,直线a、b相交于点C,点D在线段AC上,点E在线段DC上.则DE= AC ﹣ AD ﹣ EC ;
(2)画任意∠AOB,使∠AOB<180°,在∠AOB内部再任意作两条射线OC、OD,则图中共有 6 个角.
【分析】根据题意,正确画出图形,结合图形求解即可.
【解答】解:(1)DE=AC﹣AD﹣EC;
(2)6个.
【点评】考查直线、线段、射线及角的概念.解题的关键是正确画出图形,注意图形结合的解题思想.
同课章节目录
