2019秋湘教版九年级数学上册第三章图形的相似单元测试(含答案)
文档属性
| 名称 | 2019秋湘教版九年级数学上册第三章图形的相似单元测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 361.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-07 06:44:55 | ||
图片预览

文档简介
2019秋湘教版九年级数学上册第三章图形的相似单元测试
一、单选题(共10题,每题3分,共30分)
1.在相同的时刻,太阳光下物高与影长成正比.如果高为1.5米的人的影长为2.5米,那么影长为30米的旗杆的高是( ).
A.?18米?????????B.?16米??????C.?20米??????D.?15米
2.△ABC ∽△A,B,C, , 相似比为3:4,那么面积的比是_____。
A.?3:4?????B.?9:16?????C.?6:8??????D.?4:5
3.如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是(?? )
A.?2 cm2???? B.?4 cm2??????C.?8 cm2???D.?16 cm2
(第3题图) (第5题图)
4.在上科学课时,老师让同学利用手中的放大镜对蜗牛进行观察,同学们在放大镜中看到蜗牛与实际的蜗牛属于什么变换(???)。
A.?相似变换????B.?平移变换????C.?旋转变换???D.?轴对称变换
5.如图,在△ABC中,DE∥BC , ,DE=4,则BC的长是( )
A.?8???????B.?10??????C.?11???????D.?12
6.若相似△ABC与△DEF的相似比为1 :3,则△ABC与△DEF的面积比(? ? )
A.?1 :3?????B.?1 :9??? ?C.?3 :1?????D.?1 :
7.如图,在ΔABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN的长为( ? ?? )
A.?????? B.???????? ?C.???????????D.?
(第7题图) (第8题图)
8.如图,在平面直角坐标系中,点P的坐标为(0,2),直线y= 与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为(? )
A.?3? ??B.?4??????C.?5???????D.?6
9.若△ABC ∽△A′B′C′,且△ABC与△A′B′C′的相似比为1:2,则△ABC与△A′B′C′的面积比是(?? )
A.?1:1??????B.?1:2???????C.?1:3???????D.?1:4
10.若△ABC ∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为( )
A.?1:2? ?B.?2:1???????C.?1:4?????????D.?4:1
二、填空题(共6题,每题3分,共18分)
11.已知8:x =6:9,则x的值等于________。
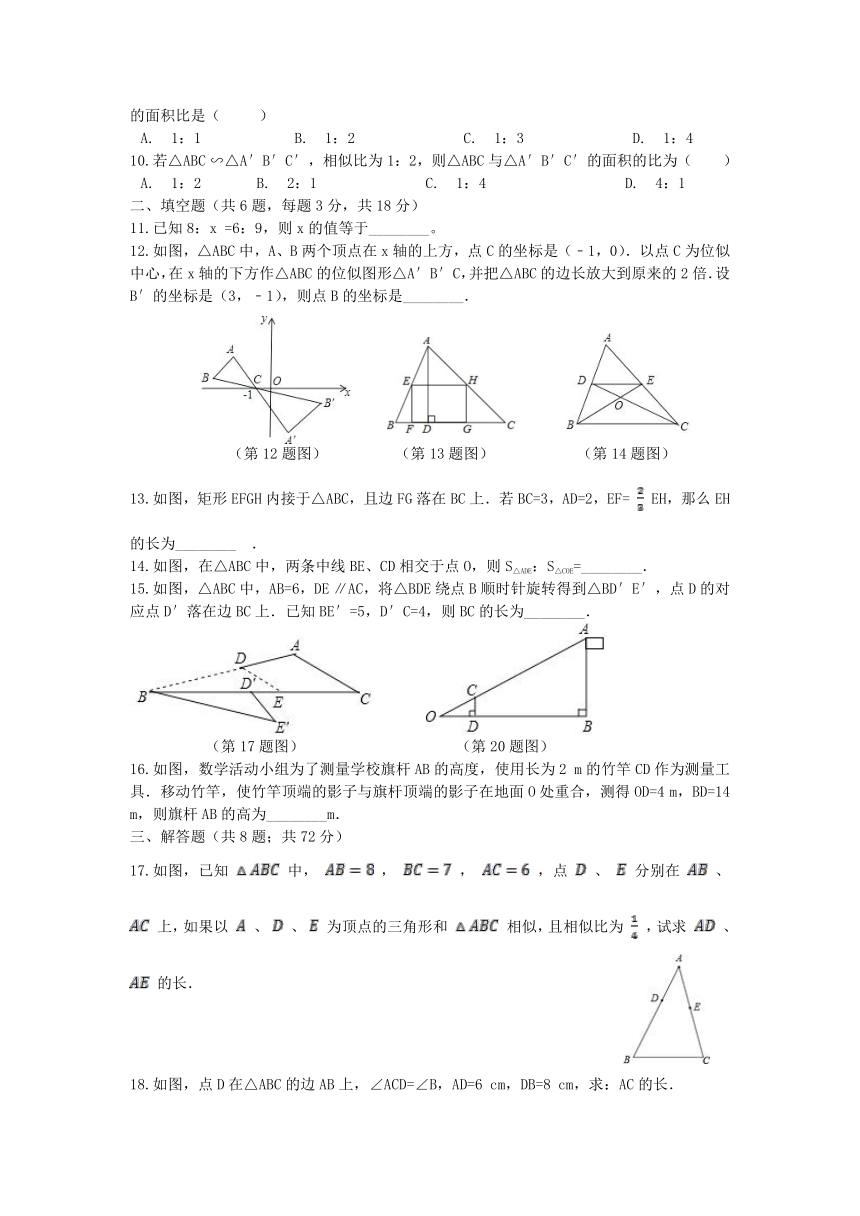
12.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,﹣1),则点B的坐标是________.
(第12题图) (第13题图) (第14题图)
13.如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF= EH,那么EH的长为________?.
14.如图,在△ABC中,两条中线BE、CD相交于点O,则S△ADE:S△COE=________.
15.如图,△ABC中,AB=6,DE ∥AC,将△BDE绕点B顺时针旋转得到△BD′E′,点D的对应点D′落在边BC上.已知BE′=5,D′C=4,则BC的长为________.
(第17题图) (第20题图)
16.如图,数学活动小组为了测量学校旗杆AB的高度,使用长为2 m的竹竿CD作为测量工具.移动竹竿,使竹竿顶端的影子与旗杆顶端的影子在地面O处重合,测得OD=4 m,BD=14 m,则旗杆AB的高为________m.
三、解答题(共8题;共72分)
17.如图,已知 中, , , ,点 、 分别在 、 上,如果以 、 、 为顶点的三角形和 相似,且相似比为 ,试求 、 的长.
18.如图,点D在△ABC的边AB上,∠ACD=∠B,AD=6 cm,DB=8 cm,求:AC的长.
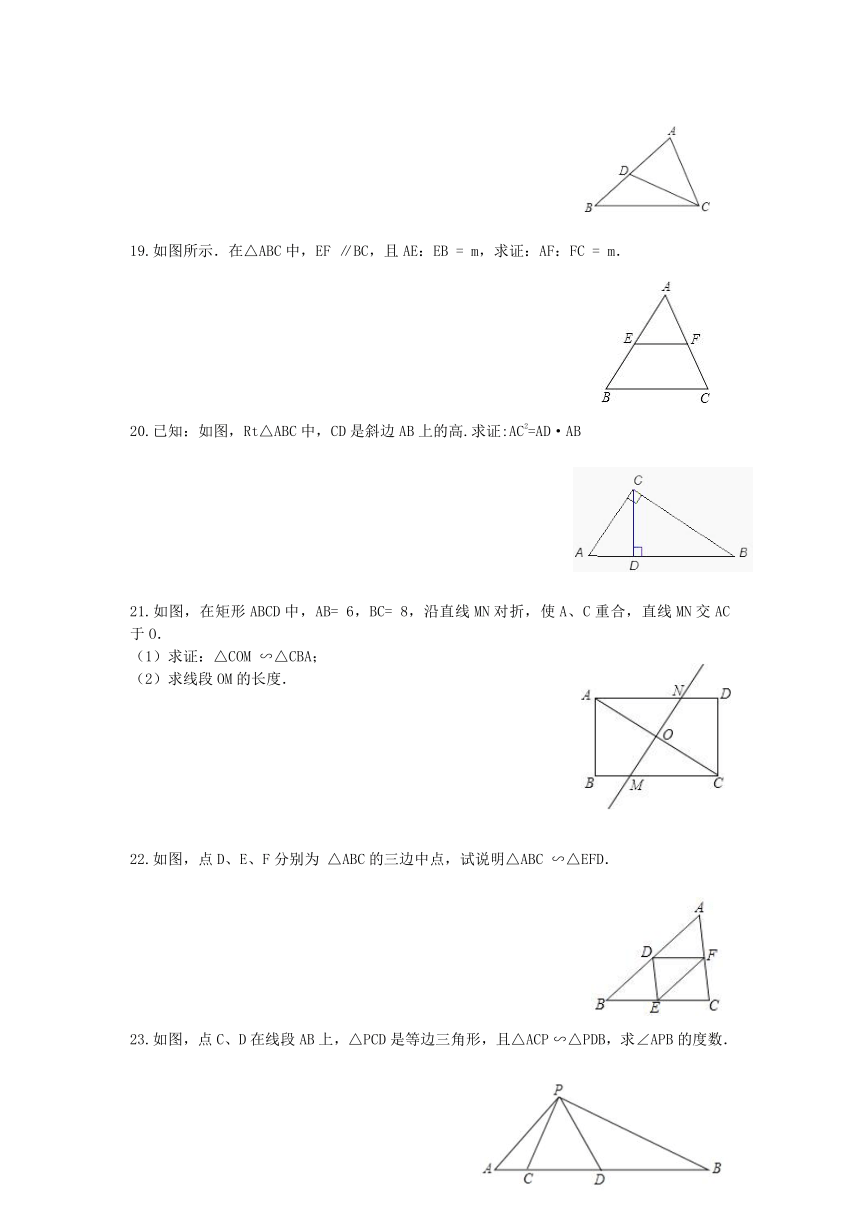
19.如图所示.在△ABC中,EF ∥BC,且AE:EB = m,求证:AF:FC = m.
20.已知:如图,Rt△ABC中,CD是斜边AB上的高.求证:AC2=AD·AB
21.如图,在矩形ABCD中,AB= 6,BC= 8,沿直线MN对折,使A、C重合,直线MN交AC于O. (1)求证:△COM ∽△CBA;???? (2)求线段OM的长度.
22.如图,点D、E、F分别为 △ABC的三边中点,试说明△ABC ∽△EFD.
23.如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP ∽△PDB,求∠APB的度数.
24.如图:已知△ABC ∽△DEC,∠D=45°,∠ACB=60°,AC=3 cm,BC=4 cm,CE=6 cm.求: (1)∠B的度数; (2)求AD的长.
参考答案
1.A 2.B 3.C 4.A 5.D 6.B 7.C 8.B 9.D 10.C
11.12 12.(﹣3, ). 13. 14. 2:1 15. 16. 9
17.解:当 时,相似比为 , ,即: ,解得: , ; 当 时, ,即: ,解得: ,
18.解:∵∠ACD=∠B,∠A=∠A,∴△ADC∽△ACB,∴ = ,即 = ,解得,AC=2 .
19.证明:∵EF∥BC,∴AF:FC=AE:EB, ∵AE:EB=m, AF:FC=m
20.证明:∵△ABC是直角三角形,CD⊥AB,∴∠A+∠B=90°,∠A+∠ACD=90°,∴∠B=∠ACD,∴△ACD∽△ABC,∴,∴AC2=AD?AB.
21.(1)证明:∵沿直线MN对折,使A、C重合,∴A与C关于直线MN对称,∴AC⊥MN,∴∠COM=90°. 在矩形ABCD中,∠B=90°,∴∠COM=∠B,又∵∠ACB=∠ACB,∴△COM∽△CBA; (2)解:∵在Rt△CBA中,AB=6,BC=8,∴AC=10,∴OC=5,∵△COM∽△CBA,∴,∴OM=.
22.证明:∵点D、E、F分别为△ABC的三边中点, ∴DE、DF、EF分别为△ABC的中位线,∴DE= AC,DF= BC,EF= AB(中位线定理),∴ ,∴△ABC∽△EFD(三边对应成比例的两个三角形相似)
23.解:∵△PCD是等边三角形,∴∠PCD=60°,∴∠ACP=120°,∵△ACP∽△PDB,∴∠APC=∠B,又∠A=∠A,∴△ACP∽△ABP,∴∠APB=∠ACP=120°.
24.解:(1)∵△ABC∽△DEC,∴∠A=∠D=45°,在△ACB中,∠B=180°﹣∠A﹣∠ACB=180°﹣45°﹣60°=75°; (2)∵△ABC∽△DEC,∴,即DC=×CE=cm,∴AD=AC+CD=cm.
一、单选题(共10题,每题3分,共30分)
1.在相同的时刻,太阳光下物高与影长成正比.如果高为1.5米的人的影长为2.5米,那么影长为30米的旗杆的高是( ).
A.?18米?????????B.?16米??????C.?20米??????D.?15米
2.△ABC ∽△A,B,C, , 相似比为3:4,那么面积的比是_____。
A.?3:4?????B.?9:16?????C.?6:8??????D.?4:5
3.如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是(?? )
A.?2 cm2???? B.?4 cm2??????C.?8 cm2???D.?16 cm2
(第3题图) (第5题图)
4.在上科学课时,老师让同学利用手中的放大镜对蜗牛进行观察,同学们在放大镜中看到蜗牛与实际的蜗牛属于什么变换(???)。
A.?相似变换????B.?平移变换????C.?旋转变换???D.?轴对称变换
5.如图,在△ABC中,DE∥BC , ,DE=4,则BC的长是( )
A.?8???????B.?10??????C.?11???????D.?12
6.若相似△ABC与△DEF的相似比为1 :3,则△ABC与△DEF的面积比(? ? )
A.?1 :3?????B.?1 :9??? ?C.?3 :1?????D.?1 :
7.如图,在ΔABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN的长为( ? ?? )
A.?????? B.???????? ?C.???????????D.?
(第7题图) (第8题图)
8.如图,在平面直角坐标系中,点P的坐标为(0,2),直线y= 与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为(? )
A.?3? ??B.?4??????C.?5???????D.?6
9.若△ABC ∽△A′B′C′,且△ABC与△A′B′C′的相似比为1:2,则△ABC与△A′B′C′的面积比是(?? )
A.?1:1??????B.?1:2???????C.?1:3???????D.?1:4
10.若△ABC ∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为( )
A.?1:2? ?B.?2:1???????C.?1:4?????????D.?4:1
二、填空题(共6题,每题3分,共18分)
11.已知8:x =6:9,则x的值等于________。
12.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,﹣1),则点B的坐标是________.
(第12题图) (第13题图) (第14题图)
13.如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF= EH,那么EH的长为________?.
14.如图,在△ABC中,两条中线BE、CD相交于点O,则S△ADE:S△COE=________.
15.如图,△ABC中,AB=6,DE ∥AC,将△BDE绕点B顺时针旋转得到△BD′E′,点D的对应点D′落在边BC上.已知BE′=5,D′C=4,则BC的长为________.
(第17题图) (第20题图)
16.如图,数学活动小组为了测量学校旗杆AB的高度,使用长为2 m的竹竿CD作为测量工具.移动竹竿,使竹竿顶端的影子与旗杆顶端的影子在地面O处重合,测得OD=4 m,BD=14 m,则旗杆AB的高为________m.
三、解答题(共8题;共72分)
17.如图,已知 中, , , ,点 、 分别在 、 上,如果以 、 、 为顶点的三角形和 相似,且相似比为 ,试求 、 的长.
18.如图,点D在△ABC的边AB上,∠ACD=∠B,AD=6 cm,DB=8 cm,求:AC的长.
19.如图所示.在△ABC中,EF ∥BC,且AE:EB = m,求证:AF:FC = m.
20.已知:如图,Rt△ABC中,CD是斜边AB上的高.求证:AC2=AD·AB
21.如图,在矩形ABCD中,AB= 6,BC= 8,沿直线MN对折,使A、C重合,直线MN交AC于O. (1)求证:△COM ∽△CBA;???? (2)求线段OM的长度.
22.如图,点D、E、F分别为 △ABC的三边中点,试说明△ABC ∽△EFD.
23.如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP ∽△PDB,求∠APB的度数.
24.如图:已知△ABC ∽△DEC,∠D=45°,∠ACB=60°,AC=3 cm,BC=4 cm,CE=6 cm.求: (1)∠B的度数; (2)求AD的长.
参考答案
1.A 2.B 3.C 4.A 5.D 6.B 7.C 8.B 9.D 10.C
11.12 12.(﹣3, ). 13. 14. 2:1 15. 16. 9
17.解:当 时,相似比为 , ,即: ,解得: , ; 当 时, ,即: ,解得: ,
18.解:∵∠ACD=∠B,∠A=∠A,∴△ADC∽△ACB,∴ = ,即 = ,解得,AC=2 .
19.证明:∵EF∥BC,∴AF:FC=AE:EB, ∵AE:EB=m, AF:FC=m
20.证明:∵△ABC是直角三角形,CD⊥AB,∴∠A+∠B=90°,∠A+∠ACD=90°,∴∠B=∠ACD,∴△ACD∽△ABC,∴,∴AC2=AD?AB.
21.(1)证明:∵沿直线MN对折,使A、C重合,∴A与C关于直线MN对称,∴AC⊥MN,∴∠COM=90°. 在矩形ABCD中,∠B=90°,∴∠COM=∠B,又∵∠ACB=∠ACB,∴△COM∽△CBA; (2)解:∵在Rt△CBA中,AB=6,BC=8,∴AC=10,∴OC=5,∵△COM∽△CBA,∴,∴OM=.
22.证明:∵点D、E、F分别为△ABC的三边中点, ∴DE、DF、EF分别为△ABC的中位线,∴DE= AC,DF= BC,EF= AB(中位线定理),∴ ,∴△ABC∽△EFD(三边对应成比例的两个三角形相似)
23.解:∵△PCD是等边三角形,∴∠PCD=60°,∴∠ACP=120°,∵△ACP∽△PDB,∴∠APC=∠B,又∠A=∠A,∴△ACP∽△ABP,∴∠APB=∠ACP=120°.
24.解:(1)∵△ABC∽△DEC,∴∠A=∠D=45°,在△ACB中,∠B=180°﹣∠A﹣∠ACB=180°﹣45°﹣60°=75°; (2)∵△ABC∽△DEC,∴,即DC=×CE=cm,∴AD=AC+CD=cm.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
