湘教版八年级数学下册1.3 直角三角形全等的判定课件(共24张)
文档属性
| 名称 | 湘教版八年级数学下册1.3 直角三角形全等的判定课件(共24张) |  | |
| 格式 | zip | ||
| 文件大小 | 600.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 10:06:54 | ||
图片预览






文档简介
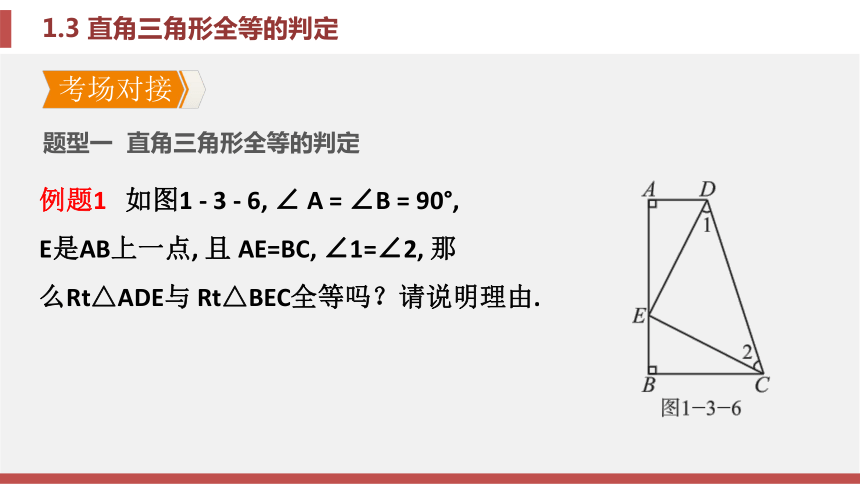
课件24张PPT。第1章 直角三角形1.3 直角三角形全等的判定 第1章 直角三角形1.3 直角三角形全等的判定 考场对接 例题1 如图1 - 3 - 6, ∠ A = ∠B = 90°,
E是AB上一点, 且 AE=BC, ∠1=∠2, 那
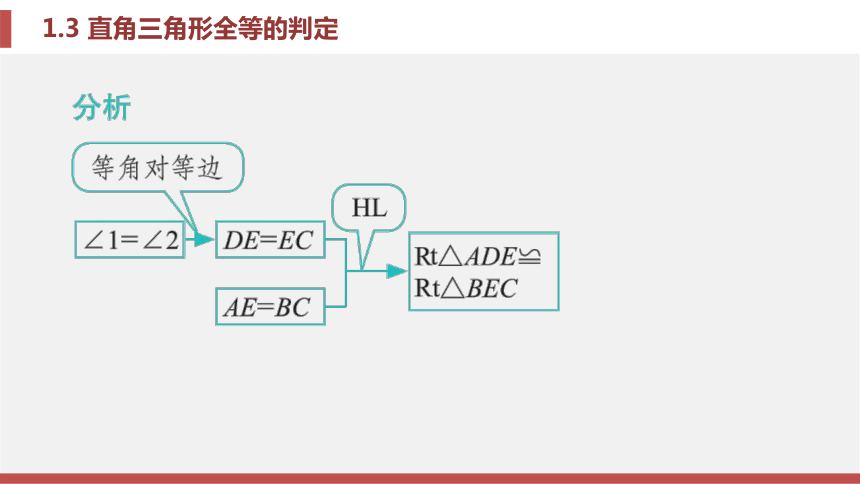
么Rt△ADE与 Rt△BEC全等吗?请说明理由.题型一 直角三角形全等的判定考场对接 解:全等. 理由如下:
∵∠1=∠2, ∴DE=EC. ∵∠A=∠B=90°,AE=BC, ∴Rt△ADE≌Rt△BEC(HL).锦囊妙计
直角三角形全等的判定方法
直角三角形全等的判定方法最多, 共有 五种:SSS, SAS, ASA, AAS, HL. 其中前四 种是通法, 后一种是特法, 只适用于直角三 角形.题型二 利用“HL”定理证明线段相等或角相等例题2 如图1-3-7所 示, AD⊥BC, CE⊥AB, 垂足 分别为D, E, AD交CE于点F, AD=CE. 求证:FA=FC.锦囊妙计
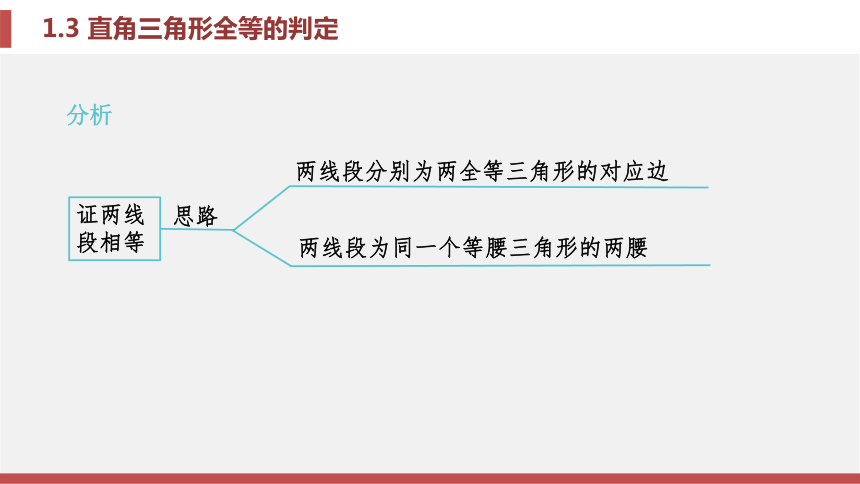
证明线段相等的常见思路
(1)证两线段所在的三角形全等;
(2)证两线段是特殊图形的特殊线段, 如等 腰三角形的腰;
(3)证两线段是两平行线间的平行线段;
(4)通过计算两线段的长度, 从数量上证明 两线段相等.题型三 三角形全等的综合应用例题3 如图1-3-8所示, 在R t△A B C中 , ∠ACB=90°, AC=BC, AE是BC边 上的中线, 过点C作CF⊥AE, 垂足 为F, 过点B作BD⊥BC, 交CF的延 长线于点D.
(1)求证:AE=CD;
(2)若AC=12 cm, 求BD的长.解: (1)证明:∵BD⊥BC, CF⊥AE, ∴∠DCB+∠D=∠DCB+∠AEC=90°, ∴∠AEC=∠D.
又∵∠ECA=∠DBC=90°, AC=BC,
∴△ECA≌△DBC(AAS), ∴AE=CD.
(2)由(1), 得△ECA≌△DBC, ∴CE=BD.
∵AE是BC边上的中线, AC=BC, ∴BD=CE= BC= AC. ∵AC=12 cm, ∴BD=6 cm.锦囊妙计
倒推法
几何证明中遇到复杂的问题常采用“倒推 法”, 即从要求证的结论出发, 寻找使结论成立 的条件①, 当条件①不具备时, 再去寻找使条件 ①成立的条件②, …, 依次类推, 直到要寻找的 条件变为已知条件, 问题即可解决. 注意解答过 程的顺序与思路分析的顺序相反.题型四 与直角三角形全等有关的动态问题例题4 如图1-3-9①, 点A, E, F, C在一条直 线上, AE=CF, 过点E, F分别作DE⊥AC, BF⊥AC, 且AB=CD.
(1)若EF与BD相交于点G, 则EG与FG相等 吗?请说明理由; (2)若将△DEC沿AC方向移动至图②所示的位 置, 其余条件不变, (1)中的结论是否仍成立?请说 明理由.(2)(1)中的结论仍成立.
理由:∵AE=CF, ∴AE-EF=CF-EF, 即AF=CE.
又∵AB=CD, ∴Rt△ABF≌Rt△CDE(HL), ∴BF=DE.
同(1)可证△DEG≌△BFG(AAS), ∴EG=FG.锦囊妙计
解决动态问题的关键
动态问题“动”中有“静”, 即图形运动到另一 情形时, 仍存在边与边、边与角、角与角之间的特殊 关系, 细心寻找边角关系是解题的关键. 一般在解 决动态问题时需要多次证明三角形全等, 此类题充 分考查了三角形全等的综合应用.题型五 与直角三角形全等有关的作图题例题5 已知一直角边和这条直角边的对角, 求作直角三角形. 已知:线段a和∠α, 如图1-3-10①. 求作:R t△ABC, 使BC = a, ∠C = 9 0°, ∠A=∠α.图1-3-10锦囊妙计
解答作图题的注意点
解答作图题一定要保留全部的作图痕迹, 包括基本作图的操作程序, 只有保留作图痕迹, 才能判断作图的操作过程是否合理.
谢 谢 观 看!
E是AB上一点, 且 AE=BC, ∠1=∠2, 那
么Rt△ADE与 Rt△BEC全等吗?请说明理由.题型一 直角三角形全等的判定考场对接 解:全等. 理由如下:
∵∠1=∠2, ∴DE=EC. ∵∠A=∠B=90°,AE=BC, ∴Rt△ADE≌Rt△BEC(HL).锦囊妙计
直角三角形全等的判定方法
直角三角形全等的判定方法最多, 共有 五种:SSS, SAS, ASA, AAS, HL. 其中前四 种是通法, 后一种是特法, 只适用于直角三 角形.题型二 利用“HL”定理证明线段相等或角相等例题2 如图1-3-7所 示, AD⊥BC, CE⊥AB, 垂足 分别为D, E, AD交CE于点F, AD=CE. 求证:FA=FC.锦囊妙计
证明线段相等的常见思路
(1)证两线段所在的三角形全等;
(2)证两线段是特殊图形的特殊线段, 如等 腰三角形的腰;
(3)证两线段是两平行线间的平行线段;
(4)通过计算两线段的长度, 从数量上证明 两线段相等.题型三 三角形全等的综合应用例题3 如图1-3-8所示, 在R t△A B C中 , ∠ACB=90°, AC=BC, AE是BC边 上的中线, 过点C作CF⊥AE, 垂足 为F, 过点B作BD⊥BC, 交CF的延 长线于点D.
(1)求证:AE=CD;
(2)若AC=12 cm, 求BD的长.解: (1)证明:∵BD⊥BC, CF⊥AE, ∴∠DCB+∠D=∠DCB+∠AEC=90°, ∴∠AEC=∠D.
又∵∠ECA=∠DBC=90°, AC=BC,
∴△ECA≌△DBC(AAS), ∴AE=CD.
(2)由(1), 得△ECA≌△DBC, ∴CE=BD.
∵AE是BC边上的中线, AC=BC, ∴BD=CE= BC= AC. ∵AC=12 cm, ∴BD=6 cm.锦囊妙计
倒推法
几何证明中遇到复杂的问题常采用“倒推 法”, 即从要求证的结论出发, 寻找使结论成立 的条件①, 当条件①不具备时, 再去寻找使条件 ①成立的条件②, …, 依次类推, 直到要寻找的 条件变为已知条件, 问题即可解决. 注意解答过 程的顺序与思路分析的顺序相反.题型四 与直角三角形全等有关的动态问题例题4 如图1-3-9①, 点A, E, F, C在一条直 线上, AE=CF, 过点E, F分别作DE⊥AC, BF⊥AC, 且AB=CD.
(1)若EF与BD相交于点G, 则EG与FG相等 吗?请说明理由; (2)若将△DEC沿AC方向移动至图②所示的位 置, 其余条件不变, (1)中的结论是否仍成立?请说 明理由.(2)(1)中的结论仍成立.
理由:∵AE=CF, ∴AE-EF=CF-EF, 即AF=CE.
又∵AB=CD, ∴Rt△ABF≌Rt△CDE(HL), ∴BF=DE.
同(1)可证△DEG≌△BFG(AAS), ∴EG=FG.锦囊妙计
解决动态问题的关键
动态问题“动”中有“静”, 即图形运动到另一 情形时, 仍存在边与边、边与角、角与角之间的特殊 关系, 细心寻找边角关系是解题的关键. 一般在解 决动态问题时需要多次证明三角形全等, 此类题充 分考查了三角形全等的综合应用.题型五 与直角三角形全等有关的作图题例题5 已知一直角边和这条直角边的对角, 求作直角三角形. 已知:线段a和∠α, 如图1-3-10①. 求作:R t△ABC, 使BC = a, ∠C = 9 0°, ∠A=∠α.图1-3-10锦囊妙计
解答作图题的注意点
解答作图题一定要保留全部的作图痕迹, 包括基本作图的操作程序, 只有保留作图痕迹, 才能判断作图的操作过程是否合理.
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
