湘教版八年级数学下册1.1 直角三角形的性质和判定(Ⅰ)课件(共23张)
文档属性
| 名称 | 湘教版八年级数学下册1.1 直角三角形的性质和判定(Ⅰ)课件(共23张) |  | |
| 格式 | zip | ||
| 文件大小 | 677.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 10:15:46 | ||
图片预览





文档简介
课件23张PPT。第1章 直角三角形1.1 直角三角形的性质和判定(Ⅰ)第1章 直角三角形1.1 直角三角形的性质
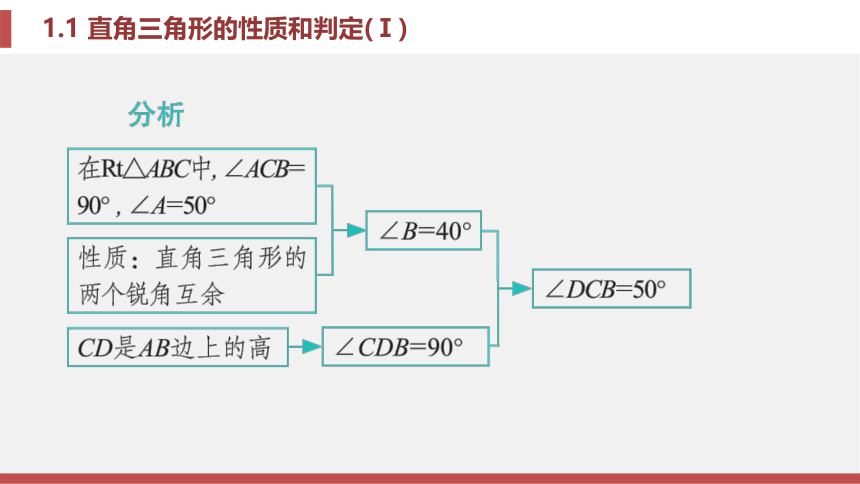
和判定(Ⅰ)考场对接 例题1 如图1-1-14, 在 Rt△ABC中, ∠ACB=90°, CD是 AB边上的高, 如果∠A=50°, 则 ∠DCB的度数为( ).
A.50° B.45°
C.40° D.25°题型一 利用直角三角形两锐角之间的关系求角度A图1-1-14锦囊妙计
直角三角形中的经典图形
在直角三角形中, 斜边上的高分直角所得的 两个锐角与原直角三角形的两个锐角之间存在 相等或互余的关系, 这是一个常见的基本图形, 在 解题中应用广泛. 如图1-1-15, ∵∠B+∠A=90°, ∠A +∠ACD = 9 0°,
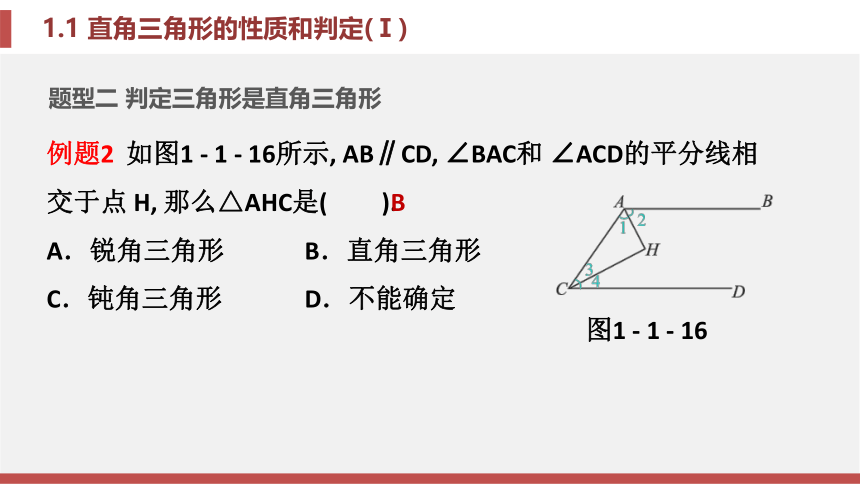
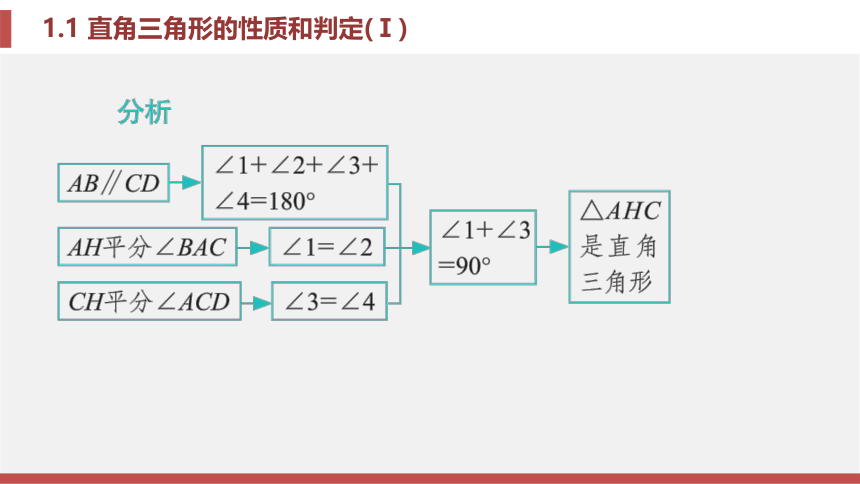
∴∠B =∠A C D . 同理 , ∠A=∠BCD.图1-1-15题型二 判定三角形是直角三角形例题2 如图1 - 1 - 16所示, AB∥CD, ∠BAC和 ∠ACD的平分线相交于点 H, 那么△AHC是( ).
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定B图1 - 1 - 16锦囊妙计
由角判定直角三角形的方法
方法1:求出或证明一个内角是直角;
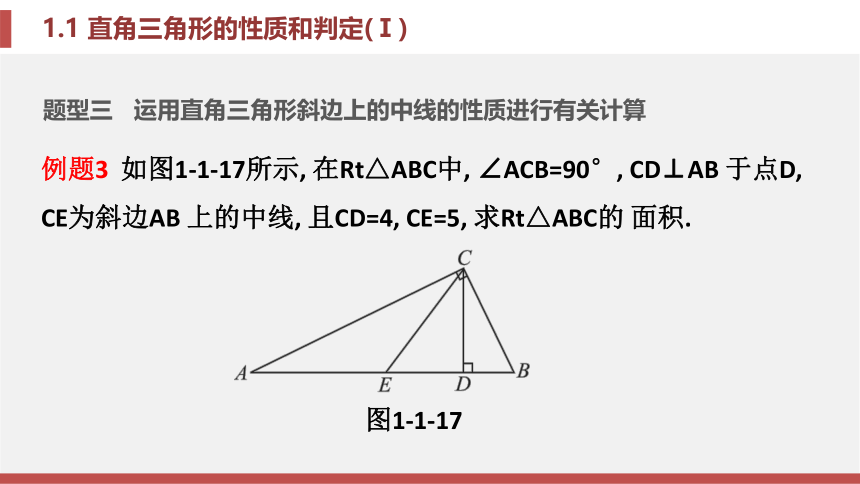
方法2:求出或证明两个内角的和等于90° (互余).题型三 运用直角三角形斜边上的中线的性质进行有关计算例题3 如图1-1-17所示, 在Rt△ABC中, ∠ACB=90°, CD⊥AB 于点D, CE为斜边AB 上的中线, 且CD=4, CE=5, 求Rt△ABC的 面积.图1-1-17解: 在Rt△ABC中, 因为CE为斜边AB上的中 线, 且CE=5,
所以CE= AB, 所以AB=2CE=10.
又因为CD⊥AB, 且CD=4,
所以S△ABC= AB·CD= ×10×4=20.锦囊妙计
求直角三角形面积的常用
方法 (1)两直角边长度乘积的一半;
(2)斜边长度与斜边上高的乘积的一半.题型四 运用直角三角形中30°角的性质进行有关计算例题4 如图 1- 1- 18 , 在 R t △ A B C 中 , ∠C=90°, ∠A=30°, BT是∠ABC的平分线, 且BT= 4 cm, 则AC等于( ).
A.2 cm B.3 cm
C.5 cm D.6 cmD锦囊妙计
含30°角的直角三角形性质的应用
(1)在直角三角形中求线段的长度时, 经常考虑 30°角所对的直角边等于斜边的一半这个性质;
(2)含30°角的直角三角形的性质是求线段 长度和证明线段倍数关系的重要依据.题型五 运用直角三角形的性质进行几何证明例题5 如图1-1-19所示, 在四边形ABCD 中, ∠ABC=∠ADC=90°, M为AC的中点, 连接BM, DM. 求证:BM=DM.证明: 因为∠ABC=∠ADC =90°,
所以△ABC和△ADC都是直角三角形.
又因为M为AC的中点, 且AC为两个直角三角形的 公共斜边,
所以BM= AC, DM= AC, 所以BM=DM.锦囊妙计
直角三角形中常作的辅助线
在直角三角形中, 如有斜边中点的条件, 应立即联想到直角三角形斜边上的中线等于斜边 的一半的性质. 连接斜边中点和直角顶点是常作 的辅助线.题型六 运用直角三角形的性质解决实际生活中的问题例题6 广场上有一座塔CD, 在平地上一点A 测得塔顶C的仰角为15°, 向塔底D前进a米到达点 B, 再测塔顶C的仰角为30°, 塔CD的高为多少米?锦囊妙计
在有关测量的问题中, 当条件比较分散, 没 有集中在同一个直角三角形中时, 要想方设法地 把分散的条件集中到同一个直角三角形中.
谢 谢 观 看!
和判定(Ⅰ)考场对接 例题1 如图1-1-14, 在 Rt△ABC中, ∠ACB=90°, CD是 AB边上的高, 如果∠A=50°, 则 ∠DCB的度数为( ).
A.50° B.45°
C.40° D.25°题型一 利用直角三角形两锐角之间的关系求角度A图1-1-14锦囊妙计
直角三角形中的经典图形
在直角三角形中, 斜边上的高分直角所得的 两个锐角与原直角三角形的两个锐角之间存在 相等或互余的关系, 这是一个常见的基本图形, 在 解题中应用广泛. 如图1-1-15, ∵∠B+∠A=90°, ∠A +∠ACD = 9 0°,
∴∠B =∠A C D . 同理 , ∠A=∠BCD.图1-1-15题型二 判定三角形是直角三角形例题2 如图1 - 1 - 16所示, AB∥CD, ∠BAC和 ∠ACD的平分线相交于点 H, 那么△AHC是( ).
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定B图1 - 1 - 16锦囊妙计
由角判定直角三角形的方法
方法1:求出或证明一个内角是直角;
方法2:求出或证明两个内角的和等于90° (互余).题型三 运用直角三角形斜边上的中线的性质进行有关计算例题3 如图1-1-17所示, 在Rt△ABC中, ∠ACB=90°, CD⊥AB 于点D, CE为斜边AB 上的中线, 且CD=4, CE=5, 求Rt△ABC的 面积.图1-1-17解: 在Rt△ABC中, 因为CE为斜边AB上的中 线, 且CE=5,
所以CE= AB, 所以AB=2CE=10.
又因为CD⊥AB, 且CD=4,
所以S△ABC= AB·CD= ×10×4=20.锦囊妙计
求直角三角形面积的常用
方法 (1)两直角边长度乘积的一半;
(2)斜边长度与斜边上高的乘积的一半.题型四 运用直角三角形中30°角的性质进行有关计算例题4 如图 1- 1- 18 , 在 R t △ A B C 中 , ∠C=90°, ∠A=30°, BT是∠ABC的平分线, 且BT= 4 cm, 则AC等于( ).
A.2 cm B.3 cm
C.5 cm D.6 cmD锦囊妙计
含30°角的直角三角形性质的应用
(1)在直角三角形中求线段的长度时, 经常考虑 30°角所对的直角边等于斜边的一半这个性质;
(2)含30°角的直角三角形的性质是求线段 长度和证明线段倍数关系的重要依据.题型五 运用直角三角形的性质进行几何证明例题5 如图1-1-19所示, 在四边形ABCD 中, ∠ABC=∠ADC=90°, M为AC的中点, 连接BM, DM. 求证:BM=DM.证明: 因为∠ABC=∠ADC =90°,
所以△ABC和△ADC都是直角三角形.
又因为M为AC的中点, 且AC为两个直角三角形的 公共斜边,
所以BM= AC, DM= AC, 所以BM=DM.锦囊妙计
直角三角形中常作的辅助线
在直角三角形中, 如有斜边中点的条件, 应立即联想到直角三角形斜边上的中线等于斜边 的一半的性质. 连接斜边中点和直角顶点是常作 的辅助线.题型六 运用直角三角形的性质解决实际生活中的问题例题6 广场上有一座塔CD, 在平地上一点A 测得塔顶C的仰角为15°, 向塔底D前进a米到达点 B, 再测塔顶C的仰角为30°, 塔CD的高为多少米?锦囊妙计
在有关测量的问题中, 当条件比较分散, 没 有集中在同一个直角三角形中时, 要想方设法地 把分散的条件集中到同一个直角三角形中.
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
