湘教版八年级数学下册1.2 直角三角形的性质和判定(Ⅱ)课件(共28张)
文档属性
| 名称 | 湘教版八年级数学下册1.2 直角三角形的性质和判定(Ⅱ)课件(共28张) |  | |
| 格式 | zip | ||
| 文件大小 | 900.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 10:17:20 | ||
图片预览






文档简介
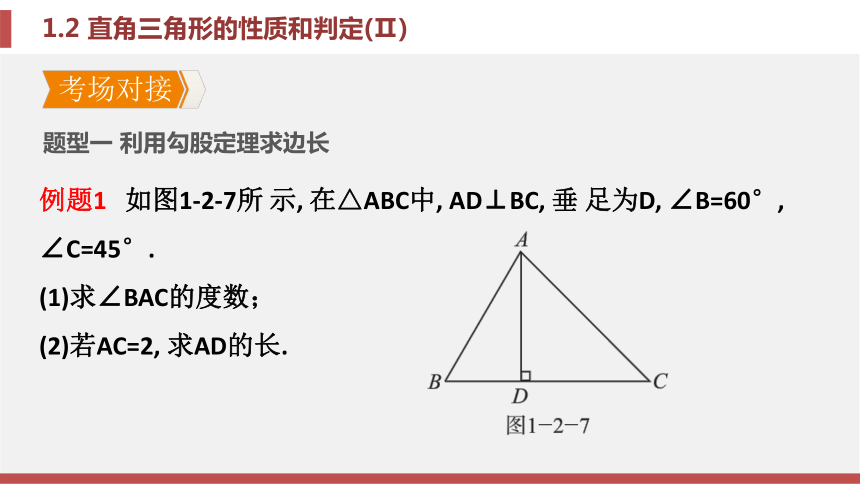
课件28张PPT。第1章 直角三角形1.2 直角三角形的性质和判定(Ⅱ)第1章 直角三角形1.2 直角三角形的性质和判定(Ⅱ)考场对接 例题1 如图1-2-7所 示, 在△ABC中, AD⊥BC, 垂 足为D, ∠B=60°, ∠C=45°.
(1)求∠BAC的度数;
(2)若AC=2, 求AD的长.题型一 利用勾股定理求边长考场对接 解: (1)∠BAC=180°-60°-45°=75°.
(2)∵AD⊥BC, ∴△ADC是直角三角形.
∵∠C=45°, ∴∠DAC=45°, ∴AD=DC.
在Rt△ADC中, AD2 +DC2 =AC2 .
∵AC=2, ∴2AD2 =4, ∴AD2 =2, ∴AD= .锦囊妙计
特殊直角三角形三边的比例关系
(1)含30°角的直角三角形(如图1-2-8)中, 三 边的比例关系为a∶b∶c=1∶ ∶2;
(2)含45°角的直角三角形
(如图1-2-9)中, 三 边的比例关系
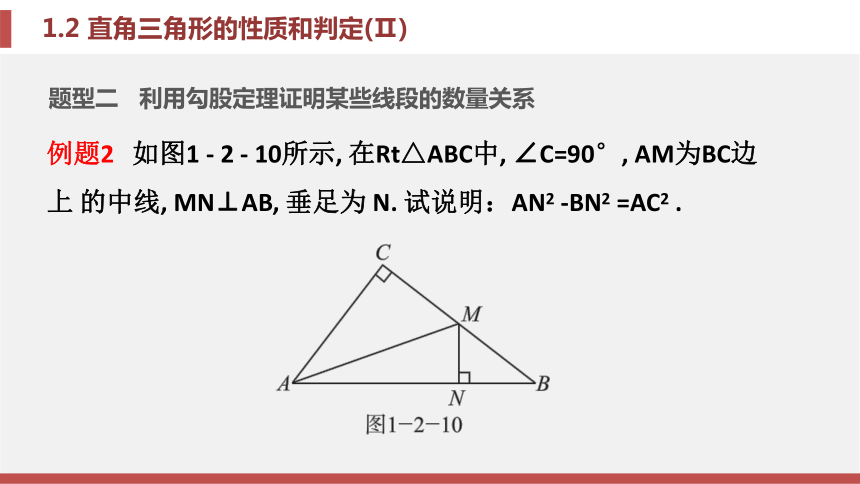
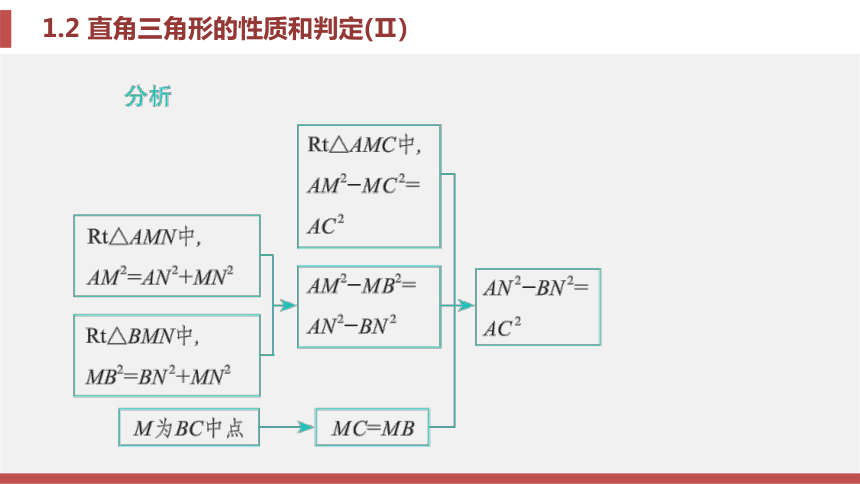
为a∶b∶c=1∶1∶ .题型二 利用勾股定理证明某些线段的数量关系例题2 如图1 - 2 - 10所示, 在Rt△ABC中, ∠C=90°, AM为BC边上 的中线, MN⊥AB, 垂足为 N. 试说明:AN2 -BN2 =AC2 .解: ∵MN⊥AB, ∴AN2 +MN2 =AM2 , BN2 +MN2 =MB2 ,
∴AN2 -BN2 =AM2 -MB2 .
∵AM为BC边上的中线, ∴MB=MC, ∴AN2 -BN2 =AM2 -MC2 .
在Rt△AMC中, AM2 -MC2 =AC2 , ∴AN2 -BN2 =AC2 .锦囊妙计
解决有关线段的平方之间的关系问题, 一 般思路是找出直角三角形, 利用勾股定理进行 转化. 若没有直角三角形, 则可通过作辅助线构 造直角三角形.题型三 利用勾股定理解决有关正方形网格问题例题3 如图1-2-11, 在由6个大小相同的小 正方形组成的网格中, 每个小正方形的边长为1.
(1)如图1-2-11①, A, B, C
是三个格点(即 小正方形
的顶点), 判断AB与BC的
关系, 并说明 理由;(2)如图1-2-11②, 连接三格和两格的对角 线, 求∠α+∠β的度数(要求:画出示意图并给出 证明).解: (1)AB⊥BC且AB=BC. 理由如下:如图1-2-12①, 连接AC.
由勾股定理, 得AB2 =12 +22 =5, BC2 =12 +22 =5, AC2 =12 +32 =10, ∴AB2 +BC2 =AC2 , AB=BC, ∴△ABC是直角三角形, ∠ABC=90°, ∴AB⊥BC, AB=BC.(2)∠α+∠β=45°. 证明如下:如图1-2-12②, 由勾股定理,
得AB2 =12 +22 =5, BC2 =12 +22 =5, AC2 =12 +32 =10,
∴AB2 +BC2 =AC2 , ∴△ABC是直角三角形. ∵AB=BC,
∴△ABC是等腰直角三角形,
∴∠BAC=45°.
由网格的性质,
可得∠α=∠1=∠2,
∴∠α+∠β=∠2+∠β=∠BAC=45°. 锦囊妙计
网格问题中的隐含条件
在正方形网格中, 有关线段的长度、图形 的面积或角度的计算问题在很多情形下都可以 转化为直角三角形问题来解决. 这类问题的条 件中隐含了使用勾股定理的条件:①网格中含 有垂直关系(直角);②网格中含有单位长度.题型四 勾股定理与图形的折叠例题4 有一块直角三角形纸片, 两直角 边AC=6 cm, BC=8 cm, 如图1-2-13所示. 现将 △ACD沿直线AD折叠(点D在BC边上), 使直角边 AC落在斜边AB上, 点C落在点E处. 求CD的长.解: ∵△ADE是由△ADC折叠得到的, ∴△ADE≌△ADC, ∴∠DEA=∠DCA=90°, DE=CD, AE=AC.
设CD=x cm(x>0), 则DE=x cm, BD=BC-CD=(8-x)cm.
∵AC=6 cm, BC=8 cm, ∴AB= =10(cm),
∴BE=AB-AE=AB-AC=10-6=4(cm).
在Rt△BDE中, 由勾股定理, 得BD2 =BE2 +DE2 ,
即(8-x)2 =42 +x2 , 解得x=3, 即CD=3 cm.锦囊妙计
解决折叠问题的常见思路
遇到图形的折叠问题, 首先要联想到图形的 全等, 有折叠过程必有全等图形. 找出全等图形, 从而可得对应边(或角)相等. 另外, 与直角三角形 有关的折叠问题, 常常以勾股定理为等量关系建 立方程求解.题型五 运用勾股定理及其逆定理证明几何问题例题5 如图1-2-14所示, 在正方形ABCD 中, F为CD的中点, E为BC边上一点, 且EC= BC. 求证:∠EFA=90°.证明:设正方形ABCD的边长 为4a(a>0), 则EC=a, BE=3a, CF=DF=2a.
在Rt△ABE中, 由勾股定理, 得 AE2 =AB2 +BE2 =(4a)2 +(3a)2 =25a2 . 在Rt△ADF中, 由勾股定理, 得 AF2 =AD2 +DF2 =(4a)2 +(2a)2 =20a2 . 在Rt△EFC中, 由勾股定理,
得 EF2 =EC2 +CF2 =a2 +(2a)2 =5a2 .
∵在△AEF中, AF2 +EF2 =20a2 +5a2 =25a2 =AE2 ,
∴△AEF为直角三角形, 且∠EFA=90°.锦囊妙计
设参法求解线段的数量关系
当图形中存在多条边之间的数量关系时, 可用“设参数法”解题, 即设最短线段的长为 常数a, 将其他线段均用含a的代数式表示出来, 从而可发现未知边之间的数量关系.题型六 运用勾股定理及其逆定理解决实际问题例题6 如图1-2-15所示, 一个长为10 m的 梯子(AB)斜靠在墙上, 梯子的顶端到地面的距离 (AO)为8 m, 梯子的顶端下滑2 m后, 底端也会滑动 2 m吗?试说明理由.解:底端会滑动2 m. 理由如下:
在Rt△AOB中, ∵AB=10 m, AO=8 m,
∴BO= =6(m).
在Rt△A′OB′中, ∵A′B′=10 m, A′O=AO-AA′=8-2=6(m),
∴B′O= =8(m),
∴BB′=B′O-BO=8-6=2(m), 即底端会滑动2 m.锦囊妙计
建模思想
在解决实际问题时, 先将其转化为几何图 形问题, 再利用相关定理求线段(角)的长度(大 小)即可.
谢 谢 观 看!
(1)求∠BAC的度数;
(2)若AC=2, 求AD的长.题型一 利用勾股定理求边长考场对接 解: (1)∠BAC=180°-60°-45°=75°.
(2)∵AD⊥BC, ∴△ADC是直角三角形.
∵∠C=45°, ∴∠DAC=45°, ∴AD=DC.
在Rt△ADC中, AD2 +DC2 =AC2 .
∵AC=2, ∴2AD2 =4, ∴AD2 =2, ∴AD= .锦囊妙计
特殊直角三角形三边的比例关系
(1)含30°角的直角三角形(如图1-2-8)中, 三 边的比例关系为a∶b∶c=1∶ ∶2;
(2)含45°角的直角三角形
(如图1-2-9)中, 三 边的比例关系
为a∶b∶c=1∶1∶ .题型二 利用勾股定理证明某些线段的数量关系例题2 如图1 - 2 - 10所示, 在Rt△ABC中, ∠C=90°, AM为BC边上 的中线, MN⊥AB, 垂足为 N. 试说明:AN2 -BN2 =AC2 .解: ∵MN⊥AB, ∴AN2 +MN2 =AM2 , BN2 +MN2 =MB2 ,
∴AN2 -BN2 =AM2 -MB2 .
∵AM为BC边上的中线, ∴MB=MC, ∴AN2 -BN2 =AM2 -MC2 .
在Rt△AMC中, AM2 -MC2 =AC2 , ∴AN2 -BN2 =AC2 .锦囊妙计
解决有关线段的平方之间的关系问题, 一 般思路是找出直角三角形, 利用勾股定理进行 转化. 若没有直角三角形, 则可通过作辅助线构 造直角三角形.题型三 利用勾股定理解决有关正方形网格问题例题3 如图1-2-11, 在由6个大小相同的小 正方形组成的网格中, 每个小正方形的边长为1.
(1)如图1-2-11①, A, B, C
是三个格点(即 小正方形
的顶点), 判断AB与BC的
关系, 并说明 理由;(2)如图1-2-11②, 连接三格和两格的对角 线, 求∠α+∠β的度数(要求:画出示意图并给出 证明).解: (1)AB⊥BC且AB=BC. 理由如下:如图1-2-12①, 连接AC.
由勾股定理, 得AB2 =12 +22 =5, BC2 =12 +22 =5, AC2 =12 +32 =10, ∴AB2 +BC2 =AC2 , AB=BC, ∴△ABC是直角三角形, ∠ABC=90°, ∴AB⊥BC, AB=BC.(2)∠α+∠β=45°. 证明如下:如图1-2-12②, 由勾股定理,
得AB2 =12 +22 =5, BC2 =12 +22 =5, AC2 =12 +32 =10,
∴AB2 +BC2 =AC2 , ∴△ABC是直角三角形. ∵AB=BC,
∴△ABC是等腰直角三角形,
∴∠BAC=45°.
由网格的性质,
可得∠α=∠1=∠2,
∴∠α+∠β=∠2+∠β=∠BAC=45°. 锦囊妙计
网格问题中的隐含条件
在正方形网格中, 有关线段的长度、图形 的面积或角度的计算问题在很多情形下都可以 转化为直角三角形问题来解决. 这类问题的条 件中隐含了使用勾股定理的条件:①网格中含 有垂直关系(直角);②网格中含有单位长度.题型四 勾股定理与图形的折叠例题4 有一块直角三角形纸片, 两直角 边AC=6 cm, BC=8 cm, 如图1-2-13所示. 现将 △ACD沿直线AD折叠(点D在BC边上), 使直角边 AC落在斜边AB上, 点C落在点E处. 求CD的长.解: ∵△ADE是由△ADC折叠得到的, ∴△ADE≌△ADC, ∴∠DEA=∠DCA=90°, DE=CD, AE=AC.
设CD=x cm(x>0), 则DE=x cm, BD=BC-CD=(8-x)cm.
∵AC=6 cm, BC=8 cm, ∴AB= =10(cm),
∴BE=AB-AE=AB-AC=10-6=4(cm).
在Rt△BDE中, 由勾股定理, 得BD2 =BE2 +DE2 ,
即(8-x)2 =42 +x2 , 解得x=3, 即CD=3 cm.锦囊妙计
解决折叠问题的常见思路
遇到图形的折叠问题, 首先要联想到图形的 全等, 有折叠过程必有全等图形. 找出全等图形, 从而可得对应边(或角)相等. 另外, 与直角三角形 有关的折叠问题, 常常以勾股定理为等量关系建 立方程求解.题型五 运用勾股定理及其逆定理证明几何问题例题5 如图1-2-14所示, 在正方形ABCD 中, F为CD的中点, E为BC边上一点, 且EC= BC. 求证:∠EFA=90°.证明:设正方形ABCD的边长 为4a(a>0), 则EC=a, BE=3a, CF=DF=2a.
在Rt△ABE中, 由勾股定理, 得 AE2 =AB2 +BE2 =(4a)2 +(3a)2 =25a2 . 在Rt△ADF中, 由勾股定理, 得 AF2 =AD2 +DF2 =(4a)2 +(2a)2 =20a2 . 在Rt△EFC中, 由勾股定理,
得 EF2 =EC2 +CF2 =a2 +(2a)2 =5a2 .
∵在△AEF中, AF2 +EF2 =20a2 +5a2 =25a2 =AE2 ,
∴△AEF为直角三角形, 且∠EFA=90°.锦囊妙计
设参法求解线段的数量关系
当图形中存在多条边之间的数量关系时, 可用“设参数法”解题, 即设最短线段的长为 常数a, 将其他线段均用含a的代数式表示出来, 从而可发现未知边之间的数量关系.题型六 运用勾股定理及其逆定理解决实际问题例题6 如图1-2-15所示, 一个长为10 m的 梯子(AB)斜靠在墙上, 梯子的顶端到地面的距离 (AO)为8 m, 梯子的顶端下滑2 m后, 底端也会滑动 2 m吗?试说明理由.解:底端会滑动2 m. 理由如下:
在Rt△AOB中, ∵AB=10 m, AO=8 m,
∴BO= =6(m).
在Rt△A′OB′中, ∵A′B′=10 m, A′O=AO-AA′=8-2=6(m),
∴B′O= =8(m),
∴BB′=B′O-BO=8-6=2(m), 即底端会滑动2 m.锦囊妙计
建模思想
在解决实际问题时, 先将其转化为几何图 形问题, 再利用相关定理求线段(角)的长度(大 小)即可.
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
