湘教版八年级数学下册2.5 矩形课件(2课时 共25张)
文档属性
| 名称 | 湘教版八年级数学下册2.5 矩形课件(2课时 共25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 698.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 00:00:00 | ||
图片预览






文档简介
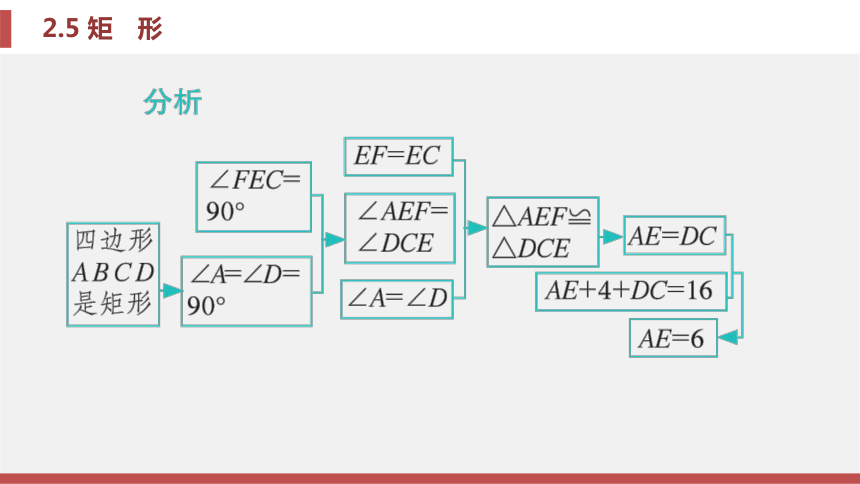
课件25张PPT。第2章 四边形2.5 矩 形第2章 四边形2.5 矩 形考场对接 例题1 如图2-5-6, 在矩形ABCD中, E是AD 上的一点, F是AB上的一点, EF⊥EC, 且EF=EC, DE=4 cm, 矩形ABCD的周长为32 cm, 求 AE的长. 题型一 运用矩形的性质求线段长解: ∵四边形ABCD是矩形, ∴∠A=∠D=90°, ∴∠DCE+∠CED=90°.
又∵EF⊥EC, ∴∠AEF+∠CED=90°, ∴∠AEF=∠DCE.
又∵EF=EC, ∴△AEF≌△DCE, ∴AE=DC.
设AE=x cm, 则DC=x cm, AD=(x+4)cm,
则有x+4+x=16, 解得x=6, 即AE的长为6 cm.锦囊妙计
求线段长度的常用方法
(1)把所要求的线段放在直角三角形中, 使 其成为某条边, 利用勾股定理或含特殊角(30°, 45°)的直角三角形的三边关系求解;
(2)利用 全等三角形的性质, 将未知线段转化为已知线 段;
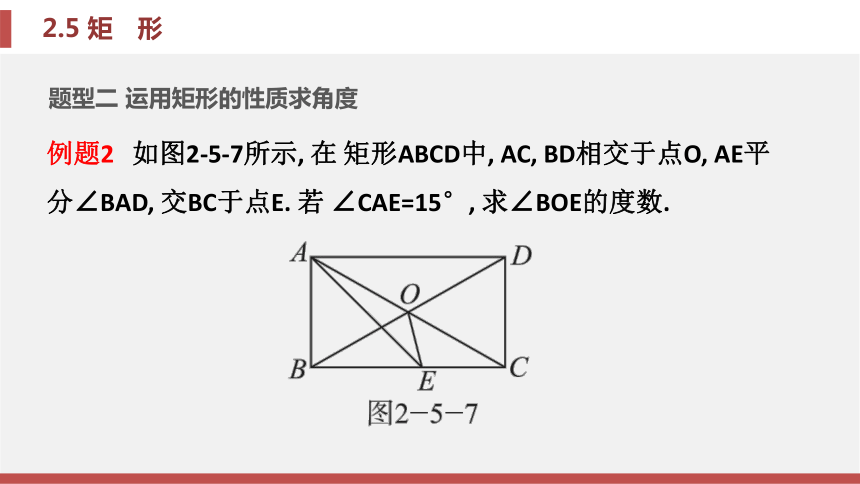
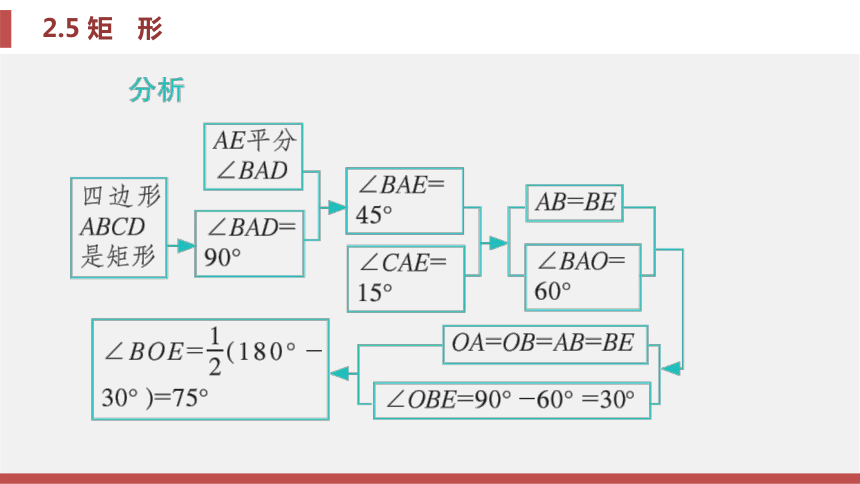
(3)利用线段的和差倍分关系求线段的长度.题型二 运用矩形的性质求角度例题2 如图2-5-7所示, 在 矩形ABCD中, AC, BD相交于点O, AE平分∠BAD, 交BC于点E. 若 ∠CAE=15°, 求∠BOE的度数. 锦囊妙计
矩形中求角度的三个关键点
在矩形中计算角度时, 常联想以下三个关 键点:①一条对角线将矩形分成两个直角三角 形, 因此可得两角间的互余关系;②利用矩形的 两条对角线能构造出等腰三角形, 因此可以得到 等角;③合理利用矩形的两组对边分别平行的 特点, 根据平行线的性质, 得出等角关系.题型三 矩形判定中的开放型问题例题3 在四边形ABCD中, AB∥DC, AB=DC. 要想该四边形成为矩形, 只需再加上一个条件是 ________________________.答案不唯一, 如∠A=90°分析 答案不唯一, 如添加条件:∠A=90°.
理由:∵AB∥DC, AB=DC, ∴四边形ABCD是平行四边形.
又∵∠A=90°, ∴平行四边形ABCD是矩形.锦囊妙计
由已知条件选合适的判定方法
判定一个四边形是矩形, 若前提条件是这 个四边形是平行四边形, 则可选用的判定方法 有:
(1)有一个角是直角的平行四边形是矩形;
(2)对角线相等的平行四边形是矩形.题型四 矩形的性质与判定的综合例题4 如图2 - 5 - 8 所 示, 四边形ABCD是平行四边形, AC, BD相交于点O, ∠1=∠2.
(1)求证:四边形ABCD是 矩形;
(2)若∠BOC=120°, AB=4 cm,
求四边形ABCD的 面积. 锦囊妙计
解决本类题时应从平行四边形的角度出发, 利用对角线相等判定 ABCD是矩形, 再结合矩 形的性质及勾股定理计算面积.题型五 有关矩形的折叠问题例题5 如图2-5-9所示, 在 矩形ABCD中, AB=8, BC=6, 将矩 形沿AC折叠, 点D落到点E处, 且 CE与AB相交于点F. 求AF的长.锦囊妙计
折叠问题中的两个关键点
折叠问题实际上就是轴对称问题, 解决折 叠问题时要抓住两点:(1)折叠前后的两个相关 的图形全等;(2)折痕垂直平分对称点所连的线 段. 求解折叠问题中线段的长度时, 一般利用勾 股定理构建方程来解决.题型六 矩形中的动点问题例题6 如图2-5-10, 在矩形ABCD中, AB= 24 cm, BC=8 cm, 点P从点A开始沿折线ABCD以 4 cm/s的速度移动, 点Q从点C开始沿CD边以2 cm/s 的速度移动. 如果点P, Q
分别从点A, C同时出发, 当 点Q
到达点D时停止运动, 点P也随之
停止运动. 设运 动时间为t s, 当t
为何值时, 四边形QPBC是矩形?解:当四边形QPBC为矩形时, 点P在边AB上.
根据题意, 得CQ=2t cm, AP=4t cm, 则BP=(24-4t)cm.
∵四边形ABCD是矩形, ∴∠B=∠C=90°, CD∥AB,
∴只有CQ=BP时, 四边形QPBC是矩形, 即2t=24-4t, 解得t=4.
答:当t=4时, 四边形QPBC是矩形.锦囊妙计
动点问题的解题策略
解决动点问题时, 要观察动点在运动过程中 图形的变化情况, 分析与理解点在不同位置的情 况, 找出相关量之间存在的关系, 并通过计算与 推理解决问题. 在变化中找到不变的性质是解决 动点问题的基本思路与方法.
谢 谢 观 看!
又∵EF⊥EC, ∴∠AEF+∠CED=90°, ∴∠AEF=∠DCE.
又∵EF=EC, ∴△AEF≌△DCE, ∴AE=DC.
设AE=x cm, 则DC=x cm, AD=(x+4)cm,
则有x+4+x=16, 解得x=6, 即AE的长为6 cm.锦囊妙计
求线段长度的常用方法
(1)把所要求的线段放在直角三角形中, 使 其成为某条边, 利用勾股定理或含特殊角(30°, 45°)的直角三角形的三边关系求解;
(2)利用 全等三角形的性质, 将未知线段转化为已知线 段;
(3)利用线段的和差倍分关系求线段的长度.题型二 运用矩形的性质求角度例题2 如图2-5-7所示, 在 矩形ABCD中, AC, BD相交于点O, AE平分∠BAD, 交BC于点E. 若 ∠CAE=15°, 求∠BOE的度数. 锦囊妙计
矩形中求角度的三个关键点
在矩形中计算角度时, 常联想以下三个关 键点:①一条对角线将矩形分成两个直角三角 形, 因此可得两角间的互余关系;②利用矩形的 两条对角线能构造出等腰三角形, 因此可以得到 等角;③合理利用矩形的两组对边分别平行的 特点, 根据平行线的性质, 得出等角关系.题型三 矩形判定中的开放型问题例题3 在四边形ABCD中, AB∥DC, AB=DC. 要想该四边形成为矩形, 只需再加上一个条件是 ________________________.答案不唯一, 如∠A=90°分析 答案不唯一, 如添加条件:∠A=90°.
理由:∵AB∥DC, AB=DC, ∴四边形ABCD是平行四边形.
又∵∠A=90°, ∴平行四边形ABCD是矩形.锦囊妙计
由已知条件选合适的判定方法
判定一个四边形是矩形, 若前提条件是这 个四边形是平行四边形, 则可选用的判定方法 有:
(1)有一个角是直角的平行四边形是矩形;
(2)对角线相等的平行四边形是矩形.题型四 矩形的性质与判定的综合例题4 如图2 - 5 - 8 所 示, 四边形ABCD是平行四边形, AC, BD相交于点O, ∠1=∠2.
(1)求证:四边形ABCD是 矩形;
(2)若∠BOC=120°, AB=4 cm,
求四边形ABCD的 面积. 锦囊妙计
解决本类题时应从平行四边形的角度出发, 利用对角线相等判定 ABCD是矩形, 再结合矩 形的性质及勾股定理计算面积.题型五 有关矩形的折叠问题例题5 如图2-5-9所示, 在 矩形ABCD中, AB=8, BC=6, 将矩 形沿AC折叠, 点D落到点E处, 且 CE与AB相交于点F. 求AF的长.锦囊妙计
折叠问题中的两个关键点
折叠问题实际上就是轴对称问题, 解决折 叠问题时要抓住两点:(1)折叠前后的两个相关 的图形全等;(2)折痕垂直平分对称点所连的线 段. 求解折叠问题中线段的长度时, 一般利用勾 股定理构建方程来解决.题型六 矩形中的动点问题例题6 如图2-5-10, 在矩形ABCD中, AB= 24 cm, BC=8 cm, 点P从点A开始沿折线ABCD以 4 cm/s的速度移动, 点Q从点C开始沿CD边以2 cm/s 的速度移动. 如果点P, Q
分别从点A, C同时出发, 当 点Q
到达点D时停止运动, 点P也随之
停止运动. 设运 动时间为t s, 当t
为何值时, 四边形QPBC是矩形?解:当四边形QPBC为矩形时, 点P在边AB上.
根据题意, 得CQ=2t cm, AP=4t cm, 则BP=(24-4t)cm.
∵四边形ABCD是矩形, ∴∠B=∠C=90°, CD∥AB,
∴只有CQ=BP时, 四边形QPBC是矩形, 即2t=24-4t, 解得t=4.
答:当t=4时, 四边形QPBC是矩形.锦囊妙计
动点问题的解题策略
解决动点问题时, 要观察动点在运动过程中 图形的变化情况, 分析与理解点在不同位置的情 况, 找出相关量之间存在的关系, 并通过计算与 推理解决问题. 在变化中找到不变的性质是解决 动点问题的基本思路与方法.
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
