湘教版八年级数学下册2.1 多边形课件(共17张)
文档属性
| 名称 | 湘教版八年级数学下册2.1 多边形课件(共17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 452.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 11:06:52 | ||
图片预览






文档简介
课件17张PPT。第2章 四边形2.1 多边形 第2章 四边形2.1 多边形 考场对接 例题1 一个多边形有9条对角线, 则这个多 边形的边数为( ).
A.6??? B.7??? C.8??? D.9题型一 多边形中的对角线问题考场对接 A分析 设这个多边形有n条边.
根据题意, 得 , ∴(n-6)(n+3)=0, 解得n1=6, n2=-3(舍去),
故这个多边形的边数为6.锦囊妙计
多边形中对角线数目的计算公式
从 n(n≥3)边形的一个顶点出发可以引 (n-3)条对角线, n个顶点可以引n(n-3)条对角线, 但是每条对角线都被重复计算了一次, 因此n边 形的对角线的总条数为 .题型二 多边形的内角和、外角和的综合应用例题2 一个正多边形的每个内角比与它相邻 的外角大60°, 求这个正多边形的边数及内角和. 解:设这个正多边形为正n边形,
则它的每 一个外角为 , 与它相邻的内角为180°- .
根据题意, 得(180°- )- =60°, 解得n=6,
故这个正多边形的边数为6, 所以其内角和为 (6-2)×180°=720°.锦囊妙计
正多边形中的两个关系
(1)正n边形的每一个外角的度数为 ;
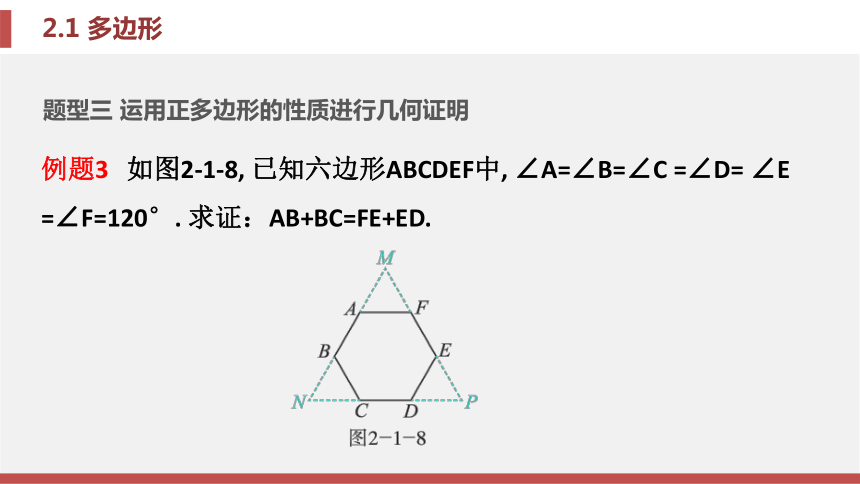
(2)n边形的每一个外角与相邻内角之间是互补 关系. 这两个关系是求解多边形问题的主要依据.题型三 运用正多边形的性质进行几何证明例题3 如图2-1-8, 已知六边形ABCDEF中, ∠A=∠B=∠C =∠D= ∠E =∠F=120°. 求证:AB+BC=FE+ED. 证明:如图2-1-8, 延长 并反向延长线段AB, CD, EF,
分别相交于点N, P, M.
依题意有△MAF, △NBC, △DEP均为等边三角形,
∴MA=MF, BN=BC, EP=ED, ∠M=∠N=∠P=60°,
∴△MNP为等边三角形, ∴MN=MP,
∴MN-MA=MP-MF, 即AN=FP, 即AB+BN=FE+EP.
又∵BN=BC, EP=ED, ∴AB+BC=FE+ED.锦囊妙计
在解决较复杂的多边形问题时, 常通过作辅 助线将多边形问题转化为三角形问题.题型四 与正多边形镶嵌有关的问题例题4 小王到瓷砖店购买一种正多边形瓷 砖铺设地面(瓷砖间要求无缝隙), 则他购买的瓷砖 形状不可以是( ).
A.正三角形 B.正方形
C.正六边形 D.正八边形D锦囊妙计
判断图形平面镶嵌的依据
判断图形是否能够平面镶嵌, 只需看拼在同一 顶点处的几个角的和是否等于360°, 若等于360°, 则说明图形能够平面镶嵌, 否则, 图形不能平面镶嵌.题型五 运用多边形内(外)角和求不规则图形的角度之和例题5 如图2-1-9所示, 则∠A+∠B+∠C+ ∠D+∠E+∠F+∠G+ ∠H+∠I+∠J的值为( ).
A.180° B.360° C.540° D.720°B锦囊妙计
转化思想在求不规则图形角度中的应用
解这类题的一般思路是把不规则图形的角通 过外角的性质转移并集中到同一个多边形中, 再利 用多边形的内(外)角和计算.
谢 谢 观 看!
A.6??? B.7??? C.8??? D.9题型一 多边形中的对角线问题考场对接 A分析 设这个多边形有n条边.
根据题意, 得 , ∴(n-6)(n+3)=0, 解得n1=6, n2=-3(舍去),
故这个多边形的边数为6.锦囊妙计
多边形中对角线数目的计算公式
从 n(n≥3)边形的一个顶点出发可以引 (n-3)条对角线, n个顶点可以引n(n-3)条对角线, 但是每条对角线都被重复计算了一次, 因此n边 形的对角线的总条数为 .题型二 多边形的内角和、外角和的综合应用例题2 一个正多边形的每个内角比与它相邻 的外角大60°, 求这个正多边形的边数及内角和. 解:设这个正多边形为正n边形,
则它的每 一个外角为 , 与它相邻的内角为180°- .
根据题意, 得(180°- )- =60°, 解得n=6,
故这个正多边形的边数为6, 所以其内角和为 (6-2)×180°=720°.锦囊妙计
正多边形中的两个关系
(1)正n边形的每一个外角的度数为 ;
(2)n边形的每一个外角与相邻内角之间是互补 关系. 这两个关系是求解多边形问题的主要依据.题型三 运用正多边形的性质进行几何证明例题3 如图2-1-8, 已知六边形ABCDEF中, ∠A=∠B=∠C =∠D= ∠E =∠F=120°. 求证:AB+BC=FE+ED. 证明:如图2-1-8, 延长 并反向延长线段AB, CD, EF,
分别相交于点N, P, M.
依题意有△MAF, △NBC, △DEP均为等边三角形,
∴MA=MF, BN=BC, EP=ED, ∠M=∠N=∠P=60°,
∴△MNP为等边三角形, ∴MN=MP,
∴MN-MA=MP-MF, 即AN=FP, 即AB+BN=FE+EP.
又∵BN=BC, EP=ED, ∴AB+BC=FE+ED.锦囊妙计
在解决较复杂的多边形问题时, 常通过作辅 助线将多边形问题转化为三角形问题.题型四 与正多边形镶嵌有关的问题例题4 小王到瓷砖店购买一种正多边形瓷 砖铺设地面(瓷砖间要求无缝隙), 则他购买的瓷砖 形状不可以是( ).
A.正三角形 B.正方形
C.正六边形 D.正八边形D锦囊妙计
判断图形平面镶嵌的依据
判断图形是否能够平面镶嵌, 只需看拼在同一 顶点处的几个角的和是否等于360°, 若等于360°, 则说明图形能够平面镶嵌, 否则, 图形不能平面镶嵌.题型五 运用多边形内(外)角和求不规则图形的角度之和例题5 如图2-1-9所示, 则∠A+∠B+∠C+ ∠D+∠E+∠F+∠G+ ∠H+∠I+∠J的值为( ).
A.180° B.360° C.540° D.720°B锦囊妙计
转化思想在求不规则图形角度中的应用
解这类题的一般思路是把不规则图形的角通 过外角的性质转移并集中到同一个多边形中, 再利 用多边形的内(外)角和计算.
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
