湘教版八年级数学下册2.3 中心对称和中心对称图形课件(共22张)
文档属性
| 名称 | 湘教版八年级数学下册2.3 中心对称和中心对称图形课件(共22张) |  | |
| 格式 | zip | ||
| 文件大小 | 581.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 14:54:49 | ||
图片预览






文档简介
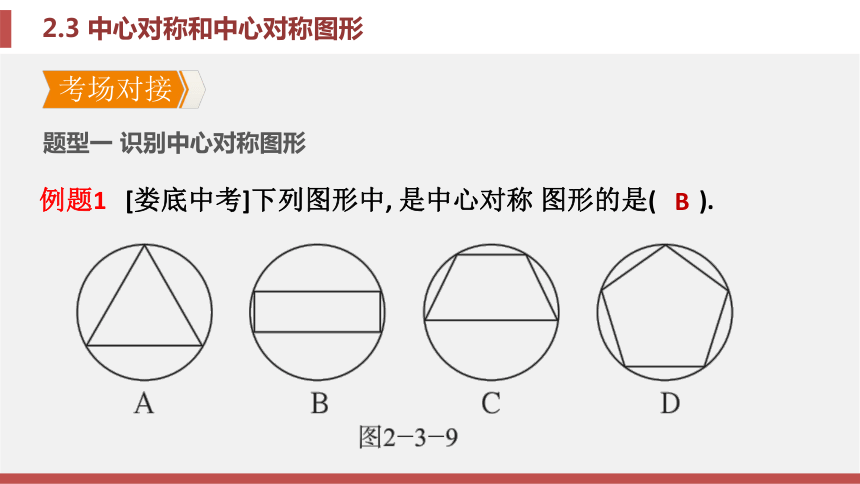
课件22张PPT。第2章 四边形2.3 中心对称和中心对称图形第2章 四边形2.3 中心对称和中心对称图形考场对接 例题1 [娄底中考]下列图形中, 是中心对称 图形的是( ).题型一 识别中心对称图形B分析锦囊妙计
识别中心对称图形的方法
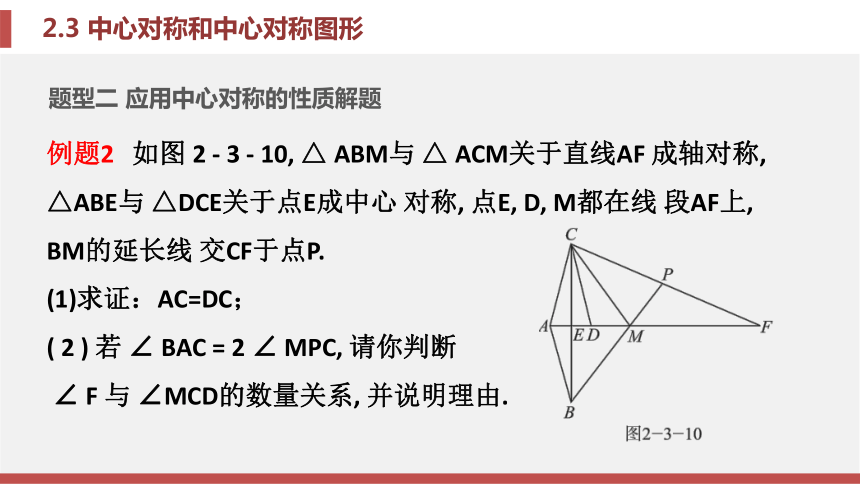
识别中心对称图形时, 最好的方法是将试 卷(或书本)倒转过来(旋转180°), 若看到的图形 与原图形一模一样, 则该图形是中心对称图形.题型二 应用中心对称的性质解题例题2 如图 2 - 3 - 10, △ ABM与 △ ACM关于直线AF 成轴对称, △ABE与 △DCE关于点E成中心 对称, 点E, D, M都在线 段AF上, BM的延长线 交CF于点P.
(1)求证:AC=DC;
( 2 ) 若 ∠ BAC = 2 ∠ MPC, 请你判断
∠ F 与 ∠MCD的数量关系, 并说明理由.解: (1)证明:∵△ABM与△ACM关于直线AF 成轴对称, ∴△ABM≌△ACM, ∴AB=AC.
又∵△ABE与△DCE关于点E成中心对称,
∴△ABE≌△DCE, ∴AB=DC, ∴AC=DC. (2)∠F=∠MCD. 理由:
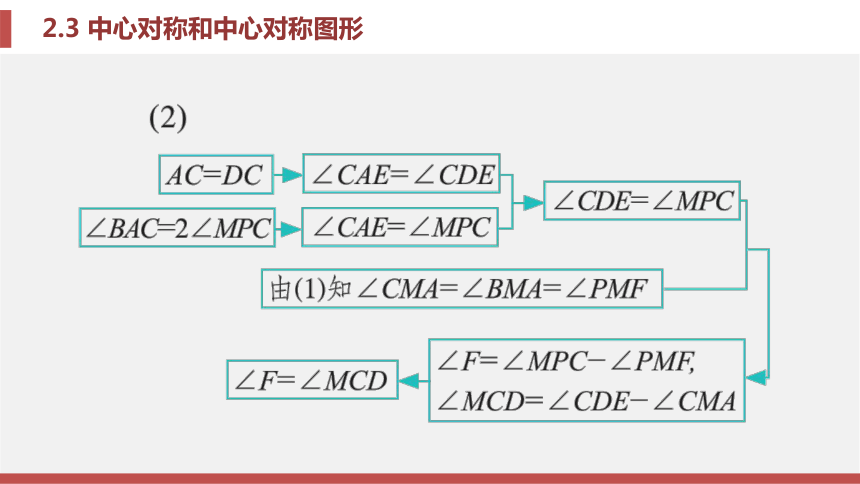
由( 1 )可得∠BAE =∠CAE =∠C D E , ∠CMA=∠BMA.
∵∠BAC=2∠MPC, ∠BMA=∠PMF,
∴∠CDE=∠MPC, ∠CMA=∠PMF.
∵∠F =∠MPC -∠PMF, ∠MCD =∠CDE - ∠CMA, ∴∠F=∠MCD. 锦囊妙计
从中心对称获取线段与角的关系
中心对称变换不改变图形的形状和大小, 因此在两个成中心对称的图形中, 必定含有相 等的线段、相等的角, 这是解题中常用的结论.题型三 网格作图例题3 如图2-3-11, 在所给网格图(每小格 均是边长为1的正方形)中完成下列问题. 作出△ABC关于点
O成中心对称的图形△A1B1C1依次连接 点A1, B1, C1在三条延长线上 分别截取OA1=OA, OB1=OB, OC1=OC锦囊妙计
中心对称作图的一般步骤
(1)连接原图形上一个关键点和对称中心;
(2)延长该关键点和对称中心的连线, 以对 称中心为端点在延长线上截取一条线段, 使其 长度等于关键点到对称中心的距离, 则线段的 另一个端点为关键点的对称点; (3)按照以上两步作出原图形上所有关键点 的对称点;
(4)将各对称点按原图形的形状依次连接起 来, 就得到与原图形关于对称中心对称的图形.题型四 用推理的方法证明一个图形是中心对称图形例题4 如图2-3-12, AC=BD, ∠A=∠B, 点E, F在AB上, 且DE∥CF, 试说明这个图形是中心对称 图形.锦囊妙计
证明中心对称图形的步骤
(1)证明各对应点的连线过对称中心(若没有 指明, 可添加辅助线作出对称中心);
(2)证明各 对应点到对称中心的距离相等.
谢 谢 观 看!
识别中心对称图形的方法
识别中心对称图形时, 最好的方法是将试 卷(或书本)倒转过来(旋转180°), 若看到的图形 与原图形一模一样, 则该图形是中心对称图形.题型二 应用中心对称的性质解题例题2 如图 2 - 3 - 10, △ ABM与 △ ACM关于直线AF 成轴对称, △ABE与 △DCE关于点E成中心 对称, 点E, D, M都在线 段AF上, BM的延长线 交CF于点P.
(1)求证:AC=DC;
( 2 ) 若 ∠ BAC = 2 ∠ MPC, 请你判断
∠ F 与 ∠MCD的数量关系, 并说明理由.解: (1)证明:∵△ABM与△ACM关于直线AF 成轴对称, ∴△ABM≌△ACM, ∴AB=AC.
又∵△ABE与△DCE关于点E成中心对称,
∴△ABE≌△DCE, ∴AB=DC, ∴AC=DC. (2)∠F=∠MCD. 理由:
由( 1 )可得∠BAE =∠CAE =∠C D E , ∠CMA=∠BMA.
∵∠BAC=2∠MPC, ∠BMA=∠PMF,
∴∠CDE=∠MPC, ∠CMA=∠PMF.
∵∠F =∠MPC -∠PMF, ∠MCD =∠CDE - ∠CMA, ∴∠F=∠MCD. 锦囊妙计
从中心对称获取线段与角的关系
中心对称变换不改变图形的形状和大小, 因此在两个成中心对称的图形中, 必定含有相 等的线段、相等的角, 这是解题中常用的结论.题型三 网格作图例题3 如图2-3-11, 在所给网格图(每小格 均是边长为1的正方形)中完成下列问题. 作出△ABC关于点
O成中心对称的图形△A1B1C1依次连接 点A1, B1, C1在三条延长线上 分别截取OA1=OA, OB1=OB, OC1=OC锦囊妙计
中心对称作图的一般步骤
(1)连接原图形上一个关键点和对称中心;
(2)延长该关键点和对称中心的连线, 以对 称中心为端点在延长线上截取一条线段, 使其 长度等于关键点到对称中心的距离, 则线段的 另一个端点为关键点的对称点; (3)按照以上两步作出原图形上所有关键点 的对称点;
(4)将各对称点按原图形的形状依次连接起 来, 就得到与原图形关于对称中心对称的图形.题型四 用推理的方法证明一个图形是中心对称图形例题4 如图2-3-12, AC=BD, ∠A=∠B, 点E, F在AB上, 且DE∥CF, 试说明这个图形是中心对称 图形.锦囊妙计
证明中心对称图形的步骤
(1)证明各对应点的连线过对称中心(若没有 指明, 可添加辅助线作出对称中心);
(2)证明各 对应点到对称中心的距离相等.
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
