湘教版数学八年级下册4.3 一次函数的图像课件(26张PPT)
文档属性
| 名称 | 湘教版数学八年级下册4.3 一次函数的图像课件(26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 576.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-07 09:19:09 | ||
图片预览







文档简介
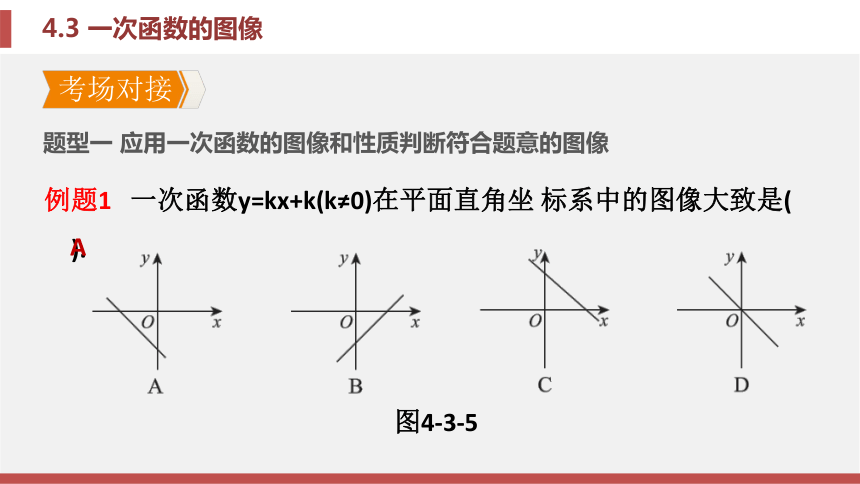
课件26张PPT。第4章 一次函数4.3 一次函数的图像第4章 一次函数4.3 一次函数的图像考场对接 例题1 一次函数y=kx+k(k≠0)在平面直角坐 标系中的图像大致是( ).题型一 应用一次函数的图像和性质判断符合题意的图像图4-3-5A锦囊妙计
判断符合条件的图像的思路
判断符合条件的图像时, 可将表达式中的k, b按符号进行讨论. 当从某一图像中获取的k, b 的符号与表达式中k, b的符号分别一致时, 该图 像必是符合题意的图像.题型二 应用一次函数的图像与性质比较大小例题2 如果点P1(3, y1), P2(2, y2)均在函数 y=2x-1的图像上, 那么
y1____ y2(填“>”“<”或“=”).分析思路(方法一)将x=2, x=3分别代入 y=2x-1, 求出y值后再比较大小(方法二)画出函数y=2x-1的图像, 根据y随x的变化情况比较大小>锦囊妙计
比较函数值大小的两种方法
(1)把自变量的值代入函数表达式求出函数 值, 比较函数值的大小;
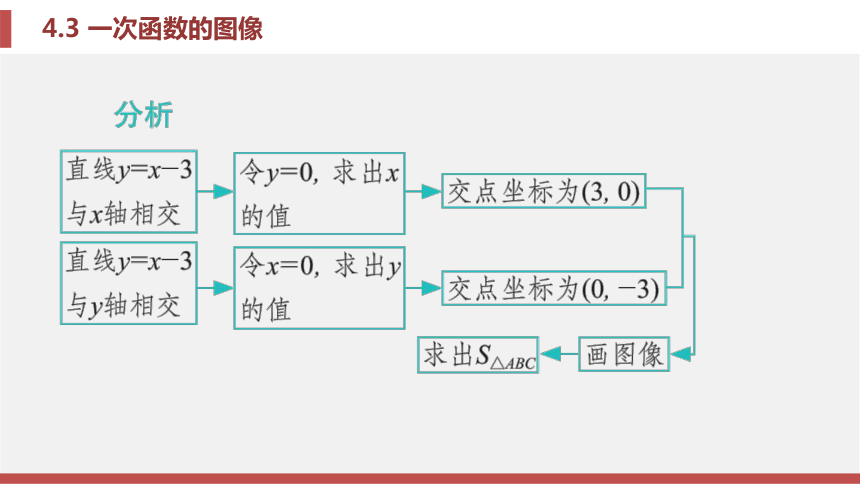
(2)通过画草图, 利用一 次函数的图像与性质比较函数值的大小.题型三 一次函数图像与坐标轴围成的三角形面积问题例题3 已知直线y=x-3与x轴交于点A, 与y轴 交于点B.
(1)求点A, B的坐标;
(2)画出直线y=x-3;
(3)求△AOB的面积.锦囊妙计
求一次函数图像与坐标轴围成的三角形面积的一般步骤
(1)求出直线与x轴, y轴的交点坐标;
(2)作出函数图像;
(3)根据图像找出三角形的底边长和底边上 的高;
(4)利用面积公式S= ×底边长×高求解.题型四 同一平面直角坐标系中的图像“共存”问题例题4 在同一平面直角坐标系下, 表示一次 函数y=mx+n与正比例函数y=mnx(m, n是常数, 且 mn≠0)的图像可能是( )图4-3-7A分析锦囊妙计
双图像问题的两种解题思路
对于双图像问题, 可假设某一图像正确, 根 据该图像判断字母系数的正负, 进而判断另一 图像是否正确;也可根据图像先判断各自系数 的正负, 若系数的符号相同, 则图像正确, 否则 不正确.题型五 一次函数图像的平移问题例题5 在平面直角坐标系内, 平 移直线y=2x-1, 请分别写出经过以下平移后直线所对应的函数表达式.
(1)向上平移3个单位长度;
(2)向左平移4个单位长度.解: (1)直线y=2x-1向上平移3个单位长度, 平 移后直线所对应的函数表达式为y=2x+2.
(2)直线y=2x-1向左平移4个单位长度, 平移后 直线所对应的函数表达式为y=2x+7. 锦囊妙计
一次函数图像的平移规律
对直线y=kx+b(k≠0)而言, 上下移动, 上加 下减;左右移动, 左加右减. 如:①向上平移h 个单位长度, 即y=kx+b+h. ②向下平移h个单位 长度, 即y=kx+b-h. ③向左平移h个单位长度, 即y=k(x+h)+b;④向右平移h个单位长度, 即 y=k(x-h)+b.题型六 几何图形与一次函数的综合例题6 如图4-3-8, 直线l:y= x+6分别交x 轴, y轴于点A, B, 点C与点 A关于y轴对称. 动点P, Q 分别在线段AC, AB上(点 P不与点A, C重合), 满足∠BPQ=∠BAO.
(1)点A的坐标是____, 点B的坐
标是____, BC=____.(2)当点P在什么位置时, △APQ≌△CBP?并 说明理由.
(3)在(2)的条件下, 可得点Q的横坐标为- , 在x轴上是否存在点M, 使得MQ+MB的值最小?如 果存在, 求出点M的坐标;如果不存在, 请说明理由.分析 (1)把x=0和y=0分别代入一次函数的表 达式, 求出点B, A的坐标, 根据勾股定理求出BC的长 即可.
(2)易证明∠PAQ=∠BCP, ∠AQP=∠CPB, 根 据点的坐标证出AP=BC, 根据全等三角形的判定 推出即可.
(3)先找到点B关于x轴对称的点B′的坐标, 把 点Q的横坐标- 代入直线l的函数表达式可求得 点Q的坐标, 再根据待定系数法可得直线B′Q的函 数表达式, 把y=0代入该函数表达式, 即可求出点M 的坐标.(2)当点P的坐标是(2, 0)时, △APQ≌△CBP.
理由:∵OA=8, P(2, 0), ∴AP=8+2=10=BC.
∵ ∠ BPQ = ∠ BAO, ∠ BAO + ∠ AQP + ∠APQ=180°, ∠APQ+∠BPQ+∠CPB=180°,
∴∠AQP=∠CPB.
∵点A和点C关于y轴对称,
∴∠PAQ=∠BCP. 锦囊妙计
与直线有关的距离之和最小值的求法
找两点中的任意一点关于直线的对称点, 连 接对称点与另一点, 与直线的交点是直线上的 要求的点, 对称点与另一点的线段长为所求的 距离之和的最小值, 常利用勾股定理求解.
谢 谢 观 看!
判断符合条件的图像的思路
判断符合条件的图像时, 可将表达式中的k, b按符号进行讨论. 当从某一图像中获取的k, b 的符号与表达式中k, b的符号分别一致时, 该图 像必是符合题意的图像.题型二 应用一次函数的图像与性质比较大小例题2 如果点P1(3, y1), P2(2, y2)均在函数 y=2x-1的图像上, 那么
y1____ y2(填“>”“<”或“=”).分析思路(方法一)将x=2, x=3分别代入 y=2x-1, 求出y值后再比较大小(方法二)画出函数y=2x-1的图像, 根据y随x的变化情况比较大小>锦囊妙计
比较函数值大小的两种方法
(1)把自变量的值代入函数表达式求出函数 值, 比较函数值的大小;
(2)通过画草图, 利用一 次函数的图像与性质比较函数值的大小.题型三 一次函数图像与坐标轴围成的三角形面积问题例题3 已知直线y=x-3与x轴交于点A, 与y轴 交于点B.
(1)求点A, B的坐标;
(2)画出直线y=x-3;
(3)求△AOB的面积.锦囊妙计
求一次函数图像与坐标轴围成的三角形面积的一般步骤
(1)求出直线与x轴, y轴的交点坐标;
(2)作出函数图像;
(3)根据图像找出三角形的底边长和底边上 的高;
(4)利用面积公式S= ×底边长×高求解.题型四 同一平面直角坐标系中的图像“共存”问题例题4 在同一平面直角坐标系下, 表示一次 函数y=mx+n与正比例函数y=mnx(m, n是常数, 且 mn≠0)的图像可能是( )图4-3-7A分析锦囊妙计
双图像问题的两种解题思路
对于双图像问题, 可假设某一图像正确, 根 据该图像判断字母系数的正负, 进而判断另一 图像是否正确;也可根据图像先判断各自系数 的正负, 若系数的符号相同, 则图像正确, 否则 不正确.题型五 一次函数图像的平移问题例题5 在平面直角坐标系内, 平 移直线y=2x-1, 请分别写出经过以下平移后直线所对应的函数表达式.
(1)向上平移3个单位长度;
(2)向左平移4个单位长度.解: (1)直线y=2x-1向上平移3个单位长度, 平 移后直线所对应的函数表达式为y=2x+2.
(2)直线y=2x-1向左平移4个单位长度, 平移后 直线所对应的函数表达式为y=2x+7. 锦囊妙计
一次函数图像的平移规律
对直线y=kx+b(k≠0)而言, 上下移动, 上加 下减;左右移动, 左加右减. 如:①向上平移h 个单位长度, 即y=kx+b+h. ②向下平移h个单位 长度, 即y=kx+b-h. ③向左平移h个单位长度, 即y=k(x+h)+b;④向右平移h个单位长度, 即 y=k(x-h)+b.题型六 几何图形与一次函数的综合例题6 如图4-3-8, 直线l:y= x+6分别交x 轴, y轴于点A, B, 点C与点 A关于y轴对称. 动点P, Q 分别在线段AC, AB上(点 P不与点A, C重合), 满足∠BPQ=∠BAO.
(1)点A的坐标是____, 点B的坐
标是____, BC=____.(2)当点P在什么位置时, △APQ≌△CBP?并 说明理由.
(3)在(2)的条件下, 可得点Q的横坐标为- , 在x轴上是否存在点M, 使得MQ+MB的值最小?如 果存在, 求出点M的坐标;如果不存在, 请说明理由.分析 (1)把x=0和y=0分别代入一次函数的表 达式, 求出点B, A的坐标, 根据勾股定理求出BC的长 即可.
(2)易证明∠PAQ=∠BCP, ∠AQP=∠CPB, 根 据点的坐标证出AP=BC, 根据全等三角形的判定 推出即可.
(3)先找到点B关于x轴对称的点B′的坐标, 把 点Q的横坐标- 代入直线l的函数表达式可求得 点Q的坐标, 再根据待定系数法可得直线B′Q的函 数表达式, 把y=0代入该函数表达式, 即可求出点M 的坐标.(2)当点P的坐标是(2, 0)时, △APQ≌△CBP.
理由:∵OA=8, P(2, 0), ∴AP=8+2=10=BC.
∵ ∠ BPQ = ∠ BAO, ∠ BAO + ∠ AQP + ∠APQ=180°, ∠APQ+∠BPQ+∠CPB=180°,
∴∠AQP=∠CPB.
∵点A和点C关于y轴对称,
∴∠PAQ=∠BCP. 锦囊妙计
与直线有关的距离之和最小值的求法
找两点中的任意一点关于直线的对称点, 连 接对称点与另一点, 与直线的交点是直线上的 要求的点, 对称点与另一点的线段长为所求的 距离之和的最小值, 常利用勾股定理求解.
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
