湘教版 八年级下册 4.5 一次函数的应用课件(30张PPT)
文档属性
| 名称 | 湘教版 八年级下册 4.5 一次函数的应用课件(30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 489.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-07 09:13:29 | ||
图片预览







文档简介
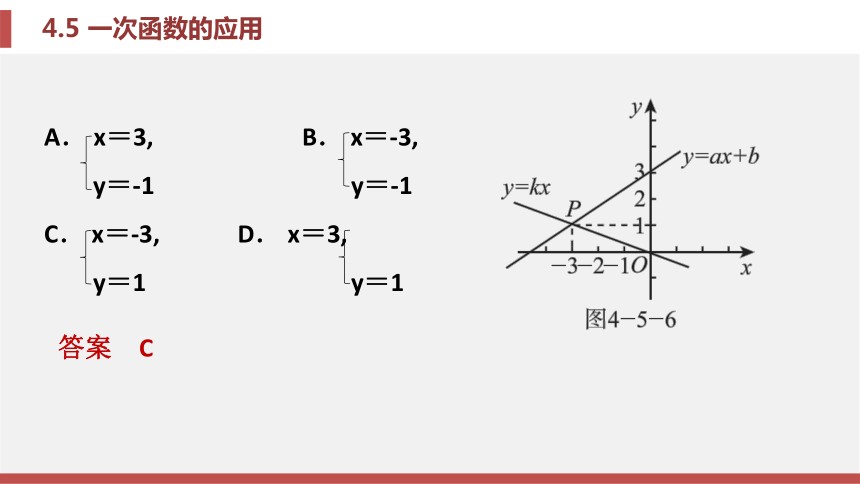
课件30张PPT。第4章 一次函数4.5 一次函数的应用第4章 一次函数4.5 一次函数的应用考场对接 例题1 [长沙模拟]如图4-5-6, 已知函 数y=ax+b(a≠0)和y=kx(k≠0)的图像相交于点 P, 则根据图像可
得, 关于x, y的二元一次方程组
y=ax+b,的解是( ).
y=kx题型一 根据函数的图像确定方程(组)的解A. x=3, B. x=-3,
y=-1 y=-1
C. x=-3, D. x=3,
y=1 y=1答案 C锦囊妙计
两直线的交点确定二元一次方程组的解
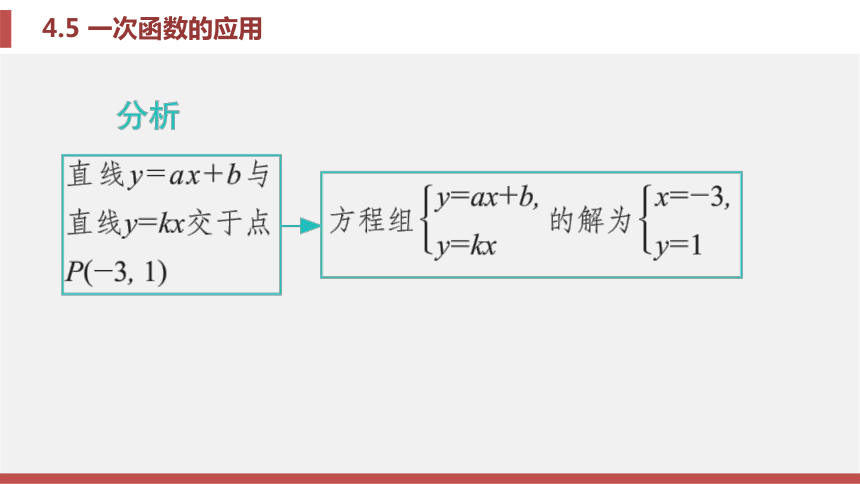
一次函数y=kx+b与y=k1x+b1的交点P(m, n )的横、纵坐标可看作是二元一次方程组 y=kx+b, 的解, 即解 x=m,
y=k1x+b1 y=n.题型二 利用一次函数的有关信息解一元一次方程或一元一次不等式例题2 已知一次函数y=ax+b(a, b是常数, 且 a≠0).x与y的部分对应值如下表:
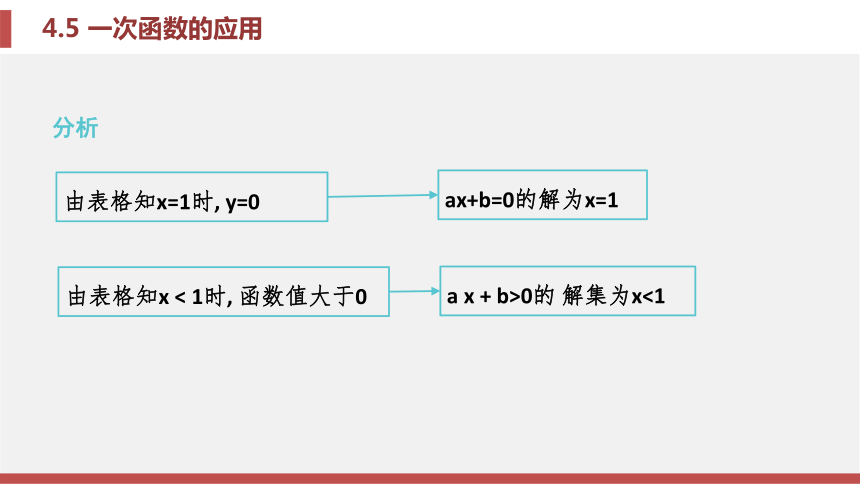
那么方程ax+b=0的解是_____, 不等式 ax+b>0的解集是_____.x=1x<1分析 a x + b>0的 解集为x<1由表格知x < 1时, 函数值大于0ax+b=0的解为x=1由表格知x=1时, y=0锦囊妙计
表格信息题的解题关键
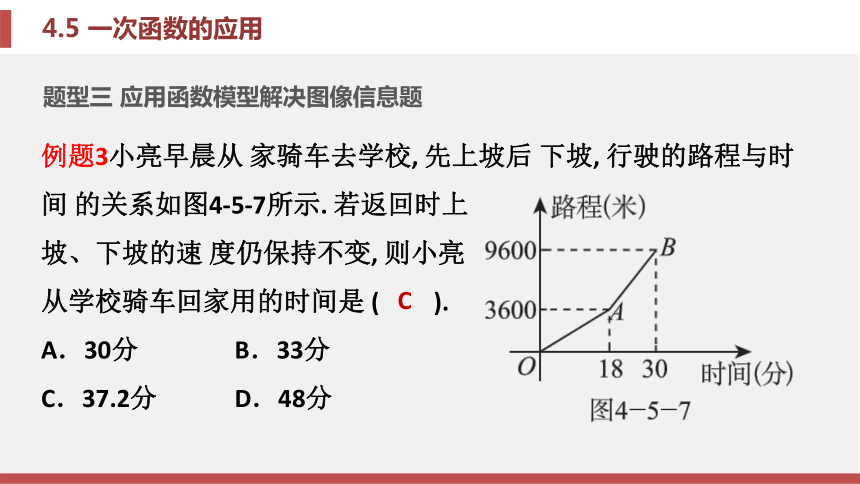
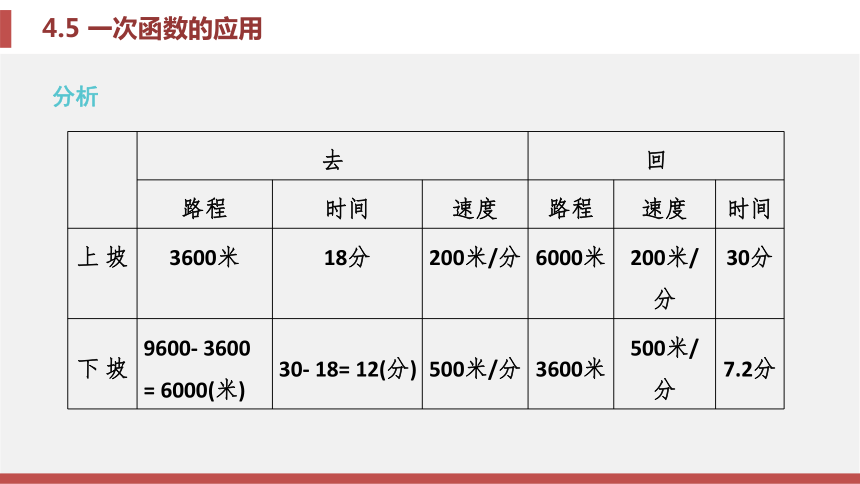
读懂表格中的信息是解题的关键. 求一元一 次方程ax+b=0的解, 实质上就是求当一次函数 y=ax+b的函数值为0时, 对应的自变量x的值;求 一元一次不等式ax+b>0的解集, 实质上就是求 当一次函数y=ax+b的函数值大于0时, 对应的自 变量x的取值范围.题型三 应用函数模型解决图像信息题例题3小亮早晨从 家骑车去学校, 先上坡后 下坡, 行驶的路程与时间 的关系如图4-5-7所示. 若返回时上
坡、下坡的速 度仍保持不变, 则小亮
从学校骑车回家用的时间是 ( ).
A.30分 B.33分
C.37.2分 D.48分C分析 锦囊妙计
解图像信息题的技巧
理解x轴、y轴所代表的含义, 读懂每一段函 数图像的意义, 学会从图像中获取有用的信息来 解题.题型四 应用函数模型求实际问题中的函数表达式, 并解决相关问题例题4 一艘轮船和一艘快艇沿相同路线从 甲港出发到乙港, 行驶过程中路程随时间变化的图 像如图4-5-8所
示, 根据图像解答下列问题.
(1)请分别求出轮船和快艇行驶的路程y(千
米) 与轮船行驶的时间x(时)之间的函数表
达式(不要求 写出自变量的取值范围);(2)轮船和快艇行驶的速度分别是多少?
(3)求快艇出发多长时间后赶上轮船.解: (1)设轮船行驶的路程y(千米)与轮船行驶 的时间x(时)之间的函数表达式为y=kx.
由图像可知, 当x=8时, y=160, 则160=8k, 解得k=20,
所以轮船行驶的路程y(千米)与轮船行驶的时间x(时)之间的函数表达式为y=20x.
设快艇行驶的路程y(千米)与轮船行驶的时间 x(时)之间的函数表达式为y=ax+b.锦囊妙计
根据图像求解问题的一般思路
在图像中找到每条直线(或线段)上的两个 已知点, 用待定系数法求出函数表达式是解题的 固有模式, 而解出的函数表达式对应的函数图像 及其性质是解决其他问题的依据.题型五 应用函数模型解决方案选择问题例题5 某公司到果园基地购买某种优质水 果慰问医务工作者, 购买量在3000千克以上(含 3000千克), 果园基地对此有两种销售方案. 甲方 案:每千克9元, 由基地送货上门;乙方案:每千 克8元, 由顾客自己租车运回. 已知该公司租车从基 地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的费用y(元) 与所购买的水果量x(千克)之间的函数表达式, 并写 出自变量x的取值范围;
(2)采用哪种购买方案费用少?并说明理由.分析 画出两个一次函数图像, 利用图像法选择方案思路2分y甲=y乙, y甲>y乙, y甲乙方案的费用y乙(元)与所购买的水果量x(千 克)之间的函数表达式为y乙=8x+5000(x≥3000).(2)解法一:①当y甲=y乙时, 有9x=8x+5000,
解得x=5000. 所以当x=5000时, 两种方案费用一样;
②当y甲所以当3000≤x<5000时, 选择甲方案费用少, 故采用甲方案;
③当y甲>y乙时,有9x>8x+5000,解得x>5000.
所以当x>5000时, 选择乙方案费用少,故采用乙方案.锦囊妙计
方案选择的两种思路
当求出每种方案的函数表达式进行方案抉 择时, 有两种思路:
(1)利用方程或不等式进行比较, 综合分析, 找到最佳方案;
(2)作出每个函数的图像, 应用函数图像的 性质进行选择.题型六 分段计费问题例题6 [南州中考]某地为了鼓励居民节约用 水, 决定实行两级收费制, 即每月用水量不超过12 吨(含12吨)时, 每吨按政府补贴优惠价收费;每月 用水量超过12吨时, 超过部分每吨按市场调节价收 费. 小黄家1月份用水24吨, 交水费42元;2月份用 水20吨, 交水费32元.
(1)求每吨水的政府补贴优惠价和市场调节价 分别是多少元? (2)设每月用水量为x吨, 应交水费为y元, 写出y 与x之间的函数表达式;
(3)小黄家3月份用水26吨, 他家应交水费多 少元?锦囊妙计
解分段计费问题的关键
解分段计费问题的关键是弄清分界点与分 段计费方式及费率. 对于选择题, 当分界点不易 找寻时, 可结合选项进行分析;对于复杂的分 段计费问题, 可借助表格进行分析.
谢 谢 观 看!
得, 关于x, y的二元一次方程组
y=ax+b,的解是( ).
y=kx题型一 根据函数的图像确定方程(组)的解A. x=3, B. x=-3,
y=-1 y=-1
C. x=-3, D. x=3,
y=1 y=1答案 C锦囊妙计
两直线的交点确定二元一次方程组的解
一次函数y=kx+b与y=k1x+b1的交点P(m, n )的横、纵坐标可看作是二元一次方程组 y=kx+b, 的解, 即解 x=m,
y=k1x+b1 y=n.题型二 利用一次函数的有关信息解一元一次方程或一元一次不等式例题2 已知一次函数y=ax+b(a, b是常数, 且 a≠0).x与y的部分对应值如下表:
那么方程ax+b=0的解是_____, 不等式 ax+b>0的解集是_____.x=1x<1分析 a x + b>0的 解集为x<1由表格知x < 1时, 函数值大于0ax+b=0的解为x=1由表格知x=1时, y=0锦囊妙计
表格信息题的解题关键
读懂表格中的信息是解题的关键. 求一元一 次方程ax+b=0的解, 实质上就是求当一次函数 y=ax+b的函数值为0时, 对应的自变量x的值;求 一元一次不等式ax+b>0的解集, 实质上就是求 当一次函数y=ax+b的函数值大于0时, 对应的自 变量x的取值范围.题型三 应用函数模型解决图像信息题例题3小亮早晨从 家骑车去学校, 先上坡后 下坡, 行驶的路程与时间 的关系如图4-5-7所示. 若返回时上
坡、下坡的速 度仍保持不变, 则小亮
从学校骑车回家用的时间是 ( ).
A.30分 B.33分
C.37.2分 D.48分C分析 锦囊妙计
解图像信息题的技巧
理解x轴、y轴所代表的含义, 读懂每一段函 数图像的意义, 学会从图像中获取有用的信息来 解题.题型四 应用函数模型求实际问题中的函数表达式, 并解决相关问题例题4 一艘轮船和一艘快艇沿相同路线从 甲港出发到乙港, 行驶过程中路程随时间变化的图 像如图4-5-8所
示, 根据图像解答下列问题.
(1)请分别求出轮船和快艇行驶的路程y(千
米) 与轮船行驶的时间x(时)之间的函数表
达式(不要求 写出自变量的取值范围);(2)轮船和快艇行驶的速度分别是多少?
(3)求快艇出发多长时间后赶上轮船.解: (1)设轮船行驶的路程y(千米)与轮船行驶 的时间x(时)之间的函数表达式为y=kx.
由图像可知, 当x=8时, y=160, 则160=8k, 解得k=20,
所以轮船行驶的路程y(千米)与轮船行驶的时间x(时)之间的函数表达式为y=20x.
设快艇行驶的路程y(千米)与轮船行驶的时间 x(时)之间的函数表达式为y=ax+b.锦囊妙计
根据图像求解问题的一般思路
在图像中找到每条直线(或线段)上的两个 已知点, 用待定系数法求出函数表达式是解题的 固有模式, 而解出的函数表达式对应的函数图像 及其性质是解决其他问题的依据.题型五 应用函数模型解决方案选择问题例题5 某公司到果园基地购买某种优质水 果慰问医务工作者, 购买量在3000千克以上(含 3000千克), 果园基地对此有两种销售方案. 甲方 案:每千克9元, 由基地送货上门;乙方案:每千 克8元, 由顾客自己租车运回. 已知该公司租车从基 地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的费用y(元) 与所购买的水果量x(千克)之间的函数表达式, 并写 出自变量x的取值范围;
(2)采用哪种购买方案费用少?并说明理由.分析 画出两个一次函数图像, 利用图像法选择方案思路2分y甲=y乙, y甲>y乙, y甲
解得x=5000. 所以当x=5000时, 两种方案费用一样;
②当y甲
③当y甲>y乙时,有9x>8x+5000,解得x>5000.
所以当x>5000时, 选择乙方案费用少,故采用乙方案.锦囊妙计
方案选择的两种思路
当求出每种方案的函数表达式进行方案抉 择时, 有两种思路:
(1)利用方程或不等式进行比较, 综合分析, 找到最佳方案;
(2)作出每个函数的图像, 应用函数图像的 性质进行选择.题型六 分段计费问题例题6 [南州中考]某地为了鼓励居民节约用 水, 决定实行两级收费制, 即每月用水量不超过12 吨(含12吨)时, 每吨按政府补贴优惠价收费;每月 用水量超过12吨时, 超过部分每吨按市场调节价收 费. 小黄家1月份用水24吨, 交水费42元;2月份用 水20吨, 交水费32元.
(1)求每吨水的政府补贴优惠价和市场调节价 分别是多少元? (2)设每月用水量为x吨, 应交水费为y元, 写出y 与x之间的函数表达式;
(3)小黄家3月份用水26吨, 他家应交水费多 少元?锦囊妙计
解分段计费问题的关键
解分段计费问题的关键是弄清分界点与分 段计费方式及费率. 对于选择题, 当分界点不易 找寻时, 可结合选项进行分析;对于复杂的分 段计费问题, 可借助表格进行分析.
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
