湘教版八年级数学下册2.2 平行四边形课件(共22张)
文档属性
| 名称 | 湘教版八年级数学下册2.2 平行四边形课件(共22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 643.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 00:00:00 | ||
图片预览







文档简介
课件22张PPT。第2章 四边形2.2 平行四边形第2章 四边形2.2 平行四边形考场对接 例题1 如图2-2-15, 四边形ABCD是平行四 边形, P是CD上一点, 且AP和BP分别平分∠DAB和 ∠CBA.
(1)求∠APB的度数;
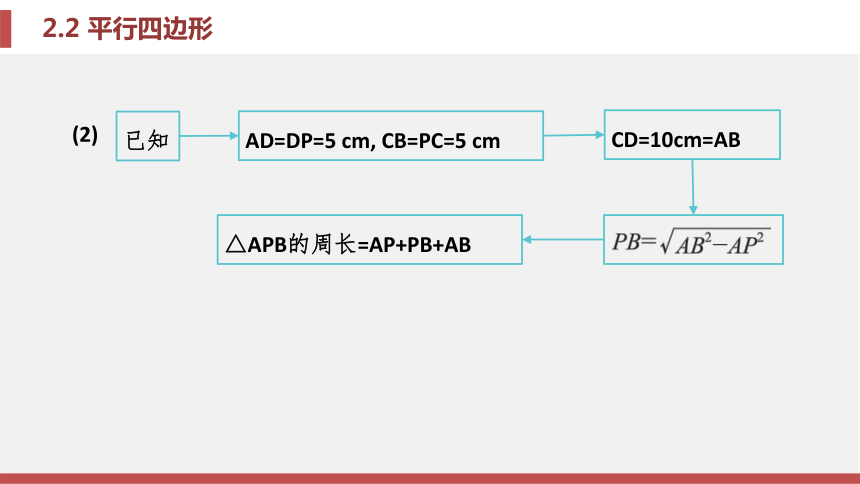
(2)如果AD=5 cm, AP=8 cm,
求△APB的周长. 题型一 应用平行四边形的性质进行有关计算考场对接 解: (1)∵四边形 ABCD是平行四边形,
∴AD∥CB, ∴∠DAB+∠CBA=180°.
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= (∠DAB+∠CBA)=90°,
∴∠APB=180°-(∠PAB+∠PBA)=90°. (2)∵AP平分∠DAB, ∴∠DAP=∠PAB.
∵四边形ABCD是平行四边形, ∴AD=CB, AB=CD, AB∥CD, ∴∠PAB=∠DPA, ∴∠DAP=∠DPA, ∴AD=DP=5 cm.
同理可得PC=CB=AD=5 cm, ∴AB=CD=DP+PC=10 cm.
在Rt△APB中, AB=10 cm, AP=8 cm, ∴PB= =6(cm),
∴△APB的周长是6+8+10=24(cm).锦囊妙计
角平分线、平行线、等腰三角形的综合
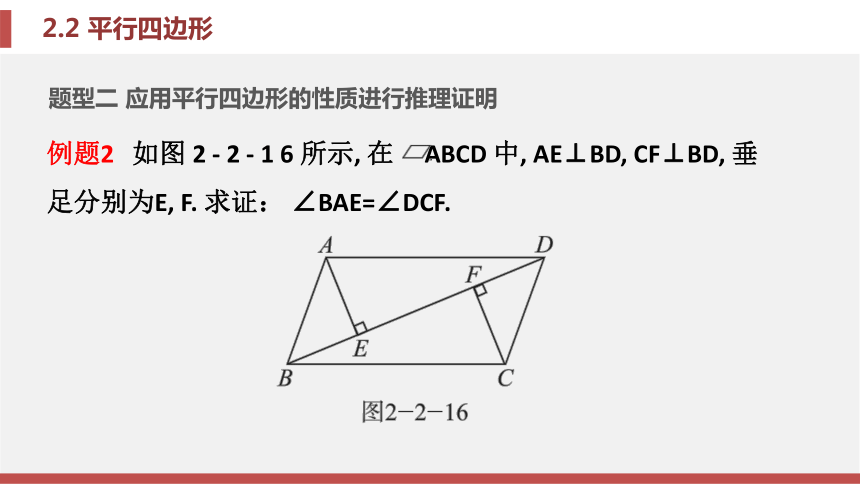
角平分线、平行线、等腰三角形经常出现 在同一个图形中, 即当角平分线、平行线、等 腰三角形中有两个图形同时出现在一个图形中, 要想到第三个图形很可能也会出现在这个图 形中.题型二 应用平行四边形的性质进行推理证明例题2 如图 2 - 2 - 1 6 所示, 在 ABCD 中, AE⊥BD, CF⊥BD, 垂足分别为E, F. 求证: ∠BAE=∠DCF.证明: ∵在 ABCD中, AB=CD, AB∥CD,
∴∠ABE=∠CDF.
又∵AE⊥BD, CF⊥BD, ∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF , ∴∠BAE=∠DCF. 锦囊妙计
利用平行四边形的性质进行证明的技巧
利用平行四边形的性质进行证明时, 通常 由平行四边形的性质得到两条线段相等, 两个 角相等, 进而证明三角形全等.题型三 选择合适的方法判定平行四边形例题3 如图2-2-17所示, 在 ABCD中, E, F 分别是AB, CD上的点, M, N分别是DE, BF的中点, ∠1=∠2.
求证:四边形ENFM是平行四边形.证明: ∵四边形ABCD是平行四边形,
∴AD=BC, ∠A=∠C, AB=CD.
又∵∠1=∠2, ∴△ADE≌△CBF, ∴DE=BF, AE=CF.
∵AB=CD, ∴BE=DF,
∴四边形EBFD是平行四边形, ∴DE∥BF.
∵M, N分别是DE, BF的中点, ∴ME=FN,
∴四边形ENFM是平行四边形.锦囊妙计
平行四边形的四种判定方法
(1)关于对角线:对角线互相平分的四边 形是平行四边形;(2)关于对边的位置关系: 两组对边分别平行的四边形是平行四边形;(3)关于对边的数量关系:两组对边分别相等的 四边形是平行四边形;(4)关于对边的数量与位 置关系:一组对边平行且相等的四边形是平行 四边形.题型四 与平行四边形的面积有关的问题例题4 如图2-2-18, 在 ABCD中, AE⊥BC 于点E, AF⊥CD于点F. 若∠EAF=60°, BE=2 cm, DF=3 cm, 求AB, BC的长及 ABCD的面积.解:在四边形AECF中,
∵∠EAF=60°, AE⊥BC, AF⊥CD,
∴∠C=360°-∠EAF-∠AEC-∠AFC= 360°-60°-90°-90°=120°.
在 ABCD中, ∵AB∥CD, AD∥BC,
∴∠B+∠C=180°, ∠C+∠D=180°, ∴∠B=∠D=60°.
在Rt△ABE中, ∠B=60°, BE=2 cm, ∴AB=4 cm,
∴CD=AB=4 cm(平行四边形的 对边相等). 同理, 在Rt△ADF中, AD=6 cm, ∴BC=AD=6 cm,锦囊妙计
解平行四边形有关面积问题的一般思路
(1)平行四边形的面积等于底乘高;
(2)平行四边形的两条对角线把平行四边形 分成面积相等的四个小三角形;
(3)平行四边形一边上的任意一点与对边端 点连线与对边所围成的三角形的面积等于平行 四边形面积的一半.
谢 谢 观 看!
(1)求∠APB的度数;
(2)如果AD=5 cm, AP=8 cm,
求△APB的周长. 题型一 应用平行四边形的性质进行有关计算考场对接 解: (1)∵四边形 ABCD是平行四边形,
∴AD∥CB, ∴∠DAB+∠CBA=180°.
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= (∠DAB+∠CBA)=90°,
∴∠APB=180°-(∠PAB+∠PBA)=90°. (2)∵AP平分∠DAB, ∴∠DAP=∠PAB.
∵四边形ABCD是平行四边形, ∴AD=CB, AB=CD, AB∥CD, ∴∠PAB=∠DPA, ∴∠DAP=∠DPA, ∴AD=DP=5 cm.
同理可得PC=CB=AD=5 cm, ∴AB=CD=DP+PC=10 cm.
在Rt△APB中, AB=10 cm, AP=8 cm, ∴PB= =6(cm),
∴△APB的周长是6+8+10=24(cm).锦囊妙计
角平分线、平行线、等腰三角形的综合
角平分线、平行线、等腰三角形经常出现 在同一个图形中, 即当角平分线、平行线、等 腰三角形中有两个图形同时出现在一个图形中, 要想到第三个图形很可能也会出现在这个图 形中.题型二 应用平行四边形的性质进行推理证明例题2 如图 2 - 2 - 1 6 所示, 在 ABCD 中, AE⊥BD, CF⊥BD, 垂足分别为E, F. 求证: ∠BAE=∠DCF.证明: ∵在 ABCD中, AB=CD, AB∥CD,
∴∠ABE=∠CDF.
又∵AE⊥BD, CF⊥BD, ∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF , ∴∠BAE=∠DCF. 锦囊妙计
利用平行四边形的性质进行证明的技巧
利用平行四边形的性质进行证明时, 通常 由平行四边形的性质得到两条线段相等, 两个 角相等, 进而证明三角形全等.题型三 选择合适的方法判定平行四边形例题3 如图2-2-17所示, 在 ABCD中, E, F 分别是AB, CD上的点, M, N分别是DE, BF的中点, ∠1=∠2.
求证:四边形ENFM是平行四边形.证明: ∵四边形ABCD是平行四边形,
∴AD=BC, ∠A=∠C, AB=CD.
又∵∠1=∠2, ∴△ADE≌△CBF, ∴DE=BF, AE=CF.
∵AB=CD, ∴BE=DF,
∴四边形EBFD是平行四边形, ∴DE∥BF.
∵M, N分别是DE, BF的中点, ∴ME=FN,
∴四边形ENFM是平行四边形.锦囊妙计
平行四边形的四种判定方法
(1)关于对角线:对角线互相平分的四边 形是平行四边形;(2)关于对边的位置关系: 两组对边分别平行的四边形是平行四边形;(3)关于对边的数量关系:两组对边分别相等的 四边形是平行四边形;(4)关于对边的数量与位 置关系:一组对边平行且相等的四边形是平行 四边形.题型四 与平行四边形的面积有关的问题例题4 如图2-2-18, 在 ABCD中, AE⊥BC 于点E, AF⊥CD于点F. 若∠EAF=60°, BE=2 cm, DF=3 cm, 求AB, BC的长及 ABCD的面积.解:在四边形AECF中,
∵∠EAF=60°, AE⊥BC, AF⊥CD,
∴∠C=360°-∠EAF-∠AEC-∠AFC= 360°-60°-90°-90°=120°.
在 ABCD中, ∵AB∥CD, AD∥BC,
∴∠B+∠C=180°, ∠C+∠D=180°, ∴∠B=∠D=60°.
在Rt△ABE中, ∠B=60°, BE=2 cm, ∴AB=4 cm,
∴CD=AB=4 cm(平行四边形的 对边相等). 同理, 在Rt△ADF中, AD=6 cm, ∴BC=AD=6 cm,锦囊妙计
解平行四边形有关面积问题的一般思路
(1)平行四边形的面积等于底乘高;
(2)平行四边形的两条对角线把平行四边形 分成面积相等的四个小三角形;
(3)平行四边形一边上的任意一点与对边端 点连线与对边所围成的三角形的面积等于平行 四边形面积的一半.
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
