湘教版八年级数学下册 4.4 用待定系数法确定一次函数表达式课件(37张PPT)
文档属性
| 名称 | 湘教版八年级数学下册 4.4 用待定系数法确定一次函数表达式课件(37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 686.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-07 00:00:00 | ||
图片预览








文档简介
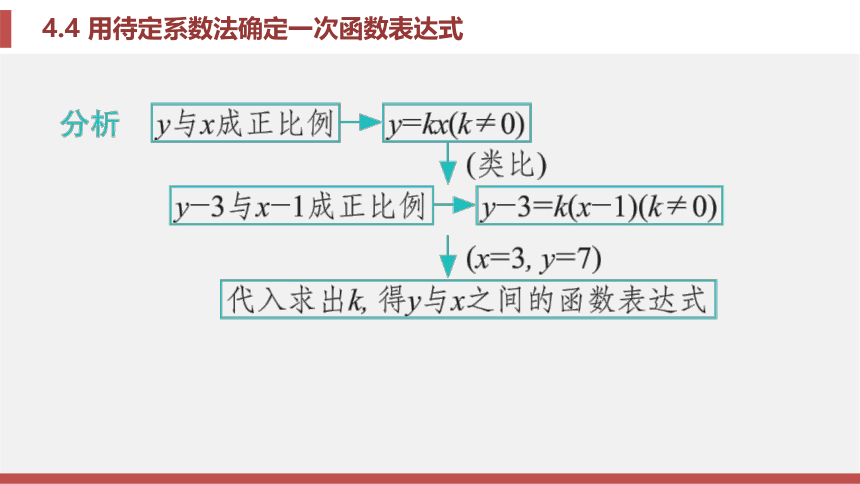
课件37张PPT。第4章 一次函数4.4 用待定系数法确定一次函数表达式第4章 一次函数4.4 用待定系数法确定一次函数表达式考场对接 例题1 已知y-3与x-1是正比例关系, 且当 x=3时, y=7.
(1)求y与x之间的函数表达式;
(2)当x=1时, 求y的值;
(3)当y=0时, 求x的值.题型一 已知两个量之间存在正比例关系,求函数表达式考场对接 解: (1)设y-3=k(x-1)(k≠0), 把x=3, y=7代入y-3=k(x-1)中,
得7-3=(3-1)k, 解得k=2.
所以y与x之间的函数表达式为y-3=2(x-1), 即y=2x+1.
(2)当x=1时, y=2×1+1=3.
(3)当y=0时, 2x+1=0, 所以x= - .锦囊妙计
已知正比例关系常见设表达式方法
变量之间存在正比例关系, 设表达式的方 法如下(其中k≠0):
(1)y与x成正比例, 设为y=kx;
(2)y与x+a成正比例, 设为y=k(x+a), 即把 (x+a)当成一个整体, 视为(1)中的x;
(3)y+b与x成正比例, 设为y+b=kx;
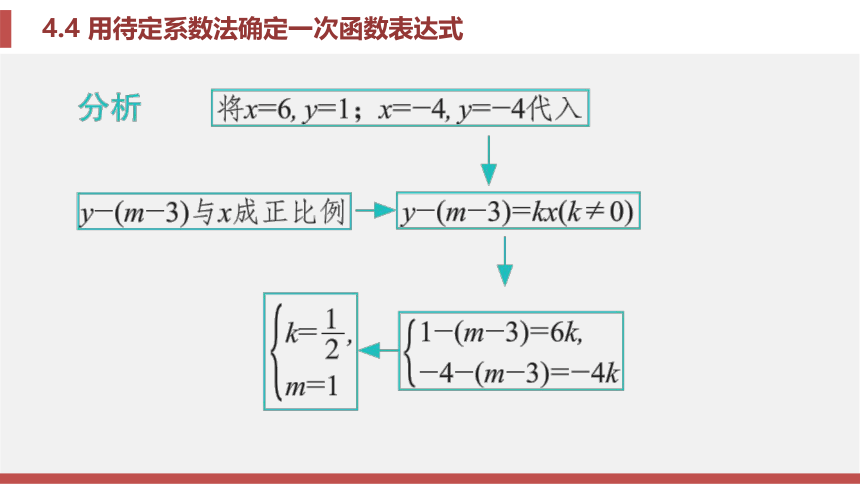
(4)y+b与x+a成正比例, 设为y+b=k(x+a).题型二 已知两对x, y的值, 求函数表达式例题2 [十堰中考]已知y-(m-3)(m是常数)与 x成正比例, 且当x=6时, y=1;当x=-4时, y=-4. 求 y与x之间的函数表达式.锦囊妙计
已知两对x, y的值求表达式的方法
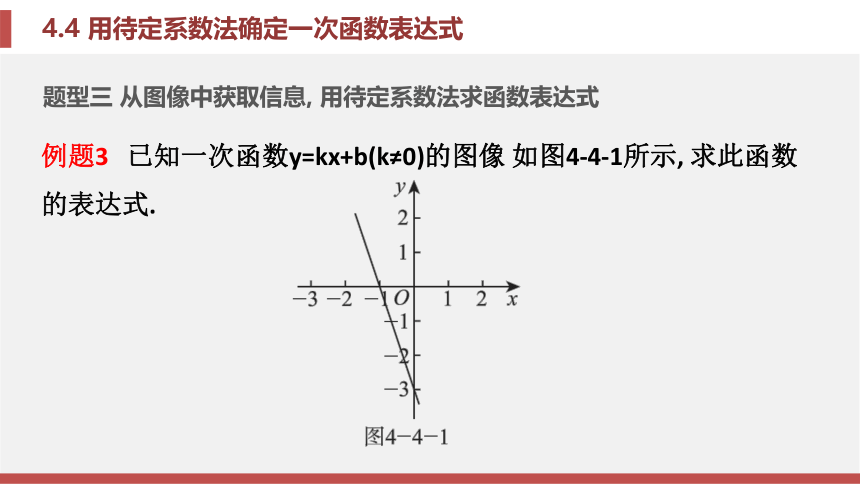
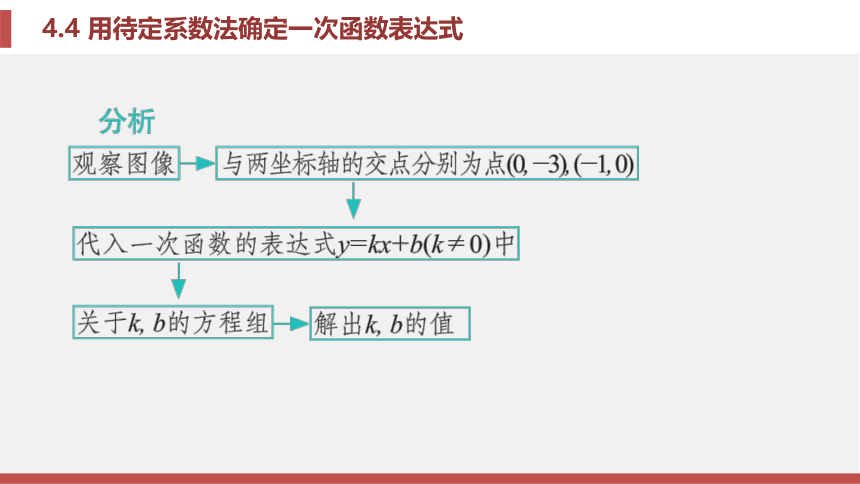
根据已知的对应关系, 设出合适的表达式, 再把两对x,y的值代入表达式, 求出待定的字母 系数即可.题型三 从图像中获取信息, 用待定系数法求函数表达式例题3 已知一次函数y=kx+b(k≠0)的图像 如图4-4-1所示, 求此函数的表达式.锦囊妙计
已知图像求表达式的方法
当给出一次函数图像求其表达式时, 应从图 像中找到两个已知点, 写出这两个点的坐标(若 图像是正比例函数的图像, 只需写出除原点外的 一个已知点的坐标即可), 再代入所设表达式中 求解.题型四 已知两直线的位置关系求函数表达式例题4 已知直线y=kx+b与直线y=- x+5平 行, 且过点A(0, -3).
(1)试求此直线所对应的函数表达式;
(2)y的值随x值的增大怎样变化?解: (1)∵直线y = k x+ b与直线 y=- x+5平行,
∴k= - . 把(0, -3)代入y= - x+ b中, 得b= -3.
∴此直线所对应的函数表达式为y= - x-3.
(2)∵k= - <0,
∴y的值随x值的增大而减小.锦囊妙计
两平行直线的特征及应用
两条直线平行, 则表达式中的k一定相等; 反之, 表达式中的k相等, 则两条直线一定平行.题型五 结合一次函数的性质求一次函数的表达式例题5 [自贡中考]已知一次函数y=kx+b, 当 1≤x≤4时, 3≤y≤6, 则 的值为________.2或–7分析 当k>0时, 函数值y随自变量x的增大而 增大.
∵当1≤x≤4时, 3≤y≤6, ∴当x=1时, y=3;当x=4时, y=6.
∴ k+b=3, 解得 k=1, ∴ =2
4k+b=6, b=2,
当k <0时, 函数值y随自变量x的增大而减小.
∵当1≤x≤4时, 3≤y≤6, ∴当x=1时, y=6;当x=4时, y=3.
∴ k+b=6, 解得 k=-1, ∴ =-7
4k+b=3, b=7, 锦囊妙计
已知x, y的取值范围求一次函数表达式的方法
已知a≤x≤b, m≤y≤n, 即已知对应线段的 两个端点坐标, 由于线段的偏转方向不定, 所以 有端点是(a, m), (b, n)和端点是(a, n), (b, m)两种 情形, 故需要分类讨论.题型六 结合几何图形的性质求一次函数的表达式例题6 在平面直角坐标 系中, 将两块全等的含90°角的 三角形纸板△ACF与△DBF按 图4-4-2所示的
方式摆放(直角 顶点F与原点O重合).
(1)求证:AE=DE;
(2)若直线DB所对应的函数表达式为
y= x+2, 求直线AC所对应的函数表达式.解: (1)证明:连接AD.
由题意可知△ACO≌△DBO,
∴AO=DO, ∠OAC=∠ODB,
∴∠OAD=∠ODA,
∴∠EAD=∠EDA, ∴AE=DE.锦囊妙计
在几何图形中运用待定系数法求一次函数 的表达式时, 要结合几何图形的性质, 如三角形 全等的性质, 等腰三角形的性质等, 确定点的坐 标, 从而确定函数表达式. 熟练掌握图形的性质 和判定定理以及待定系数法是解题的关键.题型七 与一次函数有关的几何变换例题7 已知一次函数y=2x-4与点P(-1, 2).
(1)求一次函数y=2x-4的图像关于y轴对称的 图像的函数表达式.
(2)求与直线y=2x-4关于点P(-1, 2)成中心对 称的直线的函数表达式.解: (1)一次函数y=2x-4的图像与x轴的交点坐 标为(2, 0), 与y轴的交点坐标为(0, -4).
根据关于y轴对称的点的坐标特征可得:点(0, -4)关于y轴的对称点是它本身, 点(2, 0)关于y轴的 对称点是点(-2, 0).
设与一次函数y=2x-4的图像关于y轴对称的图 像的函数表达式为y=kx-4.把(–2, 0)代入y=kx-4, 得0=-2k-4, 解得k=-2.
所以与一次函数y=2x-4的图像关 于y轴对称的图像的函数表达式为y=-2x-4.( 2 )设过点P且与直线y = 2 x - 4平行的直线 的函数表达式为y=2x+b, 把(-1, 2)代入y=2x+b, 得-2+b=2, 解得b=4, 所以y=2x+4, 直线y=2x+4与y 轴的交点坐标为(0, 4),
所以把直线y=2x-4向上平移8个单位长度得到 直线y=2x+4, 再把直线y=2x+4向上平移8个单位长 度得到直线y=2x+12,
所以与直线y=2x-4关于点P(-1, 2)成中心对称 的直线的函数表达式为y=2x+12.锦囊妙计
利用几何变换的性质求表达式的思路
(1)一次函数y=kx+b(k≠0)与y=-kx-b (k≠0)的图像关于x轴对称, 它们的交点在x轴 上;一次函数y=kx+b(k≠0)与y=-kx+b(k≠0) 的图像关于y轴对称, 它们的交点在y轴上;
(2)求与一次函数y=kx+b(k≠0)的图像关于 某点P成中心对称的图像的函数表达式时, 关键 是利用成中心对称的两条直线相互平行, 把问 题转化为直线的平移问题来解决.题型八 用待定系数法求函数表达式在实际中的应用例题8 某星期天8:00~8:30, 燃气公司给平 安加气站的储气罐注入天然气. 之后, 一位工作人 员以每车20
立方米的加气量, 依次给在加气站排队
等候的若干辆车加气.储气罐中的储气
量y(立方 米)与时间x(时)的函数关系
如图4-4-3所示.(1)8:00~8:30, 燃气公司
向储气罐注入了多少立 方米的天然气?(2)当x≥0.5时, 求储气罐中的储气量y(立方米) 关于时间x(时)的函数表达式;
(3)请你判断, 正在排队等候的第18辆车能否 在当天10:30之前加完气?并说明理由.解:(1)由图可知, 燃气公司向储气罐注入了 10 000-2000=8000(立方米)的天然气.(3)不能.理由如下:
∵给18辆车加气需天然气18×2 0=360(立 方米),
储气量为10 000-360=9640(立方米),
于是有9640=-200x+10 100, 解得x=2.3.
而从8:30到10:30经过了2小时, 显然 2<2.3.
故正在排队等候的第18辆车不能在当天10:30 之前加完气.锦囊妙计
利用函数图像解决实际问题的步骤
(1)分析题目中的已知条件, 找出题目中的 相关关系;
(2)确定函数的类型, 设出相应的函数表达式;
(3)将相关条件代入函数表达式中, 求出函数表 达式;
(4)根据函数表达式和自变量的取值情况得 出结论.
谢 谢 观 看!
(1)求y与x之间的函数表达式;
(2)当x=1时, 求y的值;
(3)当y=0时, 求x的值.题型一 已知两个量之间存在正比例关系,求函数表达式考场对接 解: (1)设y-3=k(x-1)(k≠0), 把x=3, y=7代入y-3=k(x-1)中,
得7-3=(3-1)k, 解得k=2.
所以y与x之间的函数表达式为y-3=2(x-1), 即y=2x+1.
(2)当x=1时, y=2×1+1=3.
(3)当y=0时, 2x+1=0, 所以x= - .锦囊妙计
已知正比例关系常见设表达式方法
变量之间存在正比例关系, 设表达式的方 法如下(其中k≠0):
(1)y与x成正比例, 设为y=kx;
(2)y与x+a成正比例, 设为y=k(x+a), 即把 (x+a)当成一个整体, 视为(1)中的x;
(3)y+b与x成正比例, 设为y+b=kx;
(4)y+b与x+a成正比例, 设为y+b=k(x+a).题型二 已知两对x, y的值, 求函数表达式例题2 [十堰中考]已知y-(m-3)(m是常数)与 x成正比例, 且当x=6时, y=1;当x=-4时, y=-4. 求 y与x之间的函数表达式.锦囊妙计
已知两对x, y的值求表达式的方法
根据已知的对应关系, 设出合适的表达式, 再把两对x,y的值代入表达式, 求出待定的字母 系数即可.题型三 从图像中获取信息, 用待定系数法求函数表达式例题3 已知一次函数y=kx+b(k≠0)的图像 如图4-4-1所示, 求此函数的表达式.锦囊妙计
已知图像求表达式的方法
当给出一次函数图像求其表达式时, 应从图 像中找到两个已知点, 写出这两个点的坐标(若 图像是正比例函数的图像, 只需写出除原点外的 一个已知点的坐标即可), 再代入所设表达式中 求解.题型四 已知两直线的位置关系求函数表达式例题4 已知直线y=kx+b与直线y=- x+5平 行, 且过点A(0, -3).
(1)试求此直线所对应的函数表达式;
(2)y的值随x值的增大怎样变化?解: (1)∵直线y = k x+ b与直线 y=- x+5平行,
∴k= - . 把(0, -3)代入y= - x+ b中, 得b= -3.
∴此直线所对应的函数表达式为y= - x-3.
(2)∵k= - <0,
∴y的值随x值的增大而减小.锦囊妙计
两平行直线的特征及应用
两条直线平行, 则表达式中的k一定相等; 反之, 表达式中的k相等, 则两条直线一定平行.题型五 结合一次函数的性质求一次函数的表达式例题5 [自贡中考]已知一次函数y=kx+b, 当 1≤x≤4时, 3≤y≤6, 则 的值为________.2或–7分析 当k>0时, 函数值y随自变量x的增大而 增大.
∵当1≤x≤4时, 3≤y≤6, ∴当x=1时, y=3;当x=4时, y=6.
∴ k+b=3, 解得 k=1, ∴ =2
4k+b=6, b=2,
当k <0时, 函数值y随自变量x的增大而减小.
∵当1≤x≤4时, 3≤y≤6, ∴当x=1时, y=6;当x=4时, y=3.
∴ k+b=6, 解得 k=-1, ∴ =-7
4k+b=3, b=7, 锦囊妙计
已知x, y的取值范围求一次函数表达式的方法
已知a≤x≤b, m≤y≤n, 即已知对应线段的 两个端点坐标, 由于线段的偏转方向不定, 所以 有端点是(a, m), (b, n)和端点是(a, n), (b, m)两种 情形, 故需要分类讨论.题型六 结合几何图形的性质求一次函数的表达式例题6 在平面直角坐标 系中, 将两块全等的含90°角的 三角形纸板△ACF与△DBF按 图4-4-2所示的
方式摆放(直角 顶点F与原点O重合).
(1)求证:AE=DE;
(2)若直线DB所对应的函数表达式为
y= x+2, 求直线AC所对应的函数表达式.解: (1)证明:连接AD.
由题意可知△ACO≌△DBO,
∴AO=DO, ∠OAC=∠ODB,
∴∠OAD=∠ODA,
∴∠EAD=∠EDA, ∴AE=DE.锦囊妙计
在几何图形中运用待定系数法求一次函数 的表达式时, 要结合几何图形的性质, 如三角形 全等的性质, 等腰三角形的性质等, 确定点的坐 标, 从而确定函数表达式. 熟练掌握图形的性质 和判定定理以及待定系数法是解题的关键.题型七 与一次函数有关的几何变换例题7 已知一次函数y=2x-4与点P(-1, 2).
(1)求一次函数y=2x-4的图像关于y轴对称的 图像的函数表达式.
(2)求与直线y=2x-4关于点P(-1, 2)成中心对 称的直线的函数表达式.解: (1)一次函数y=2x-4的图像与x轴的交点坐 标为(2, 0), 与y轴的交点坐标为(0, -4).
根据关于y轴对称的点的坐标特征可得:点(0, -4)关于y轴的对称点是它本身, 点(2, 0)关于y轴的 对称点是点(-2, 0).
设与一次函数y=2x-4的图像关于y轴对称的图 像的函数表达式为y=kx-4.把(–2, 0)代入y=kx-4, 得0=-2k-4, 解得k=-2.
所以与一次函数y=2x-4的图像关 于y轴对称的图像的函数表达式为y=-2x-4.( 2 )设过点P且与直线y = 2 x - 4平行的直线 的函数表达式为y=2x+b, 把(-1, 2)代入y=2x+b, 得-2+b=2, 解得b=4, 所以y=2x+4, 直线y=2x+4与y 轴的交点坐标为(0, 4),
所以把直线y=2x-4向上平移8个单位长度得到 直线y=2x+4, 再把直线y=2x+4向上平移8个单位长 度得到直线y=2x+12,
所以与直线y=2x-4关于点P(-1, 2)成中心对称 的直线的函数表达式为y=2x+12.锦囊妙计
利用几何变换的性质求表达式的思路
(1)一次函数y=kx+b(k≠0)与y=-kx-b (k≠0)的图像关于x轴对称, 它们的交点在x轴 上;一次函数y=kx+b(k≠0)与y=-kx+b(k≠0) 的图像关于y轴对称, 它们的交点在y轴上;
(2)求与一次函数y=kx+b(k≠0)的图像关于 某点P成中心对称的图像的函数表达式时, 关键 是利用成中心对称的两条直线相互平行, 把问 题转化为直线的平移问题来解决.题型八 用待定系数法求函数表达式在实际中的应用例题8 某星期天8:00~8:30, 燃气公司给平 安加气站的储气罐注入天然气. 之后, 一位工作人 员以每车20
立方米的加气量, 依次给在加气站排队
等候的若干辆车加气.储气罐中的储气
量y(立方 米)与时间x(时)的函数关系
如图4-4-3所示.(1)8:00~8:30, 燃气公司
向储气罐注入了多少立 方米的天然气?(2)当x≥0.5时, 求储气罐中的储气量y(立方米) 关于时间x(时)的函数表达式;
(3)请你判断, 正在排队等候的第18辆车能否 在当天10:30之前加完气?并说明理由.解:(1)由图可知, 燃气公司向储气罐注入了 10 000-2000=8000(立方米)的天然气.(3)不能.理由如下:
∵给18辆车加气需天然气18×2 0=360(立 方米),
储气量为10 000-360=9640(立方米),
于是有9640=-200x+10 100, 解得x=2.3.
而从8:30到10:30经过了2小时, 显然 2<2.3.
故正在排队等候的第18辆车不能在当天10:30 之前加完气.锦囊妙计
利用函数图像解决实际问题的步骤
(1)分析题目中的已知条件, 找出题目中的 相关关系;
(2)确定函数的类型, 设出相应的函数表达式;
(3)将相关条件代入函数表达式中, 求出函数表 达式;
(4)根据函数表达式和自变量的取值情况得 出结论.
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
