湘教版八年级数学下册 第4章 一次函数章末复习课件(共62张)
文档属性
| 名称 | 湘教版八年级数学下册 第4章 一次函数章末复习课件(共62张) |

|
|
| 格式 | zip | ||
| 文件大小 | 795.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-07 00:00:00 | ||
图片预览


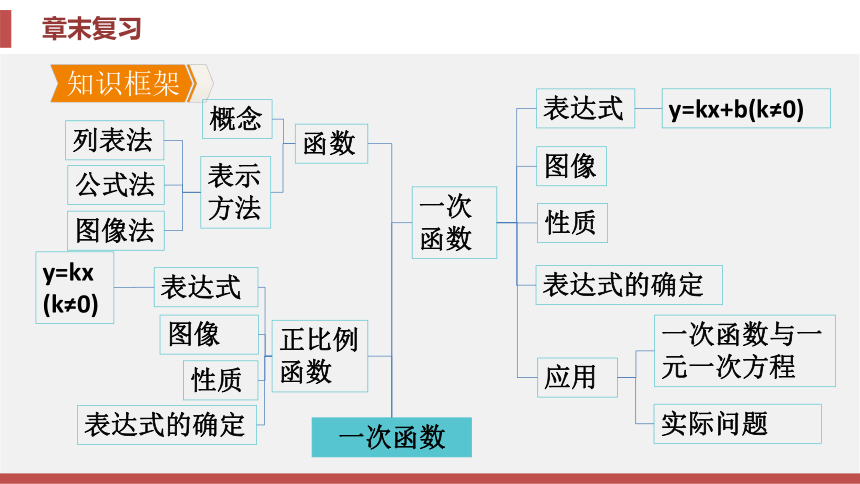









文档简介
课件62张PPT。第4章 一次函数章末复习第4章 一次函数章末复习知识框架归纳整合素养提升中考链接知识框架【要点指导】确定一个图像反映的是不是函数关系, 关键是利用定 义, 判断给出一个自变量的值, 是否有唯一确定的函数值与之对应. 函数的 实质是两个变量之间的关系, 自变量每取一个值, 因变量都有唯一确定的 值与之对应.归纳整合专题一 函数概念型问题例1 下列图形中的曲线不表示y是x的函数的是( ). C分析 依据函数的定义判断图像表示的是不是函数关系, 易知C选项中的曲 线不表示y是x的函数, 因为C选项的图像中一个x值对应一个或两个y值, 不符合 函数的定义. 相关题1 [泸州中考]下列曲线中不 能表示y是x的函数的是 ( ).C图4-Z-2【要点指导】一次函数的图像和性质是函数的重要内容, 是中考的 重要考点, 特别是与函数的增减性有关的问题更是历年中考的热点, 解题 的关键是明确一次函数y=kx+b中, 当k>0时, y的值随着x值的增大而增 大, 图像必过第一、三象限;当k 0时, y的值随着x值的增大而减小, 图像 必过第二、四象限. 专题二 一次函数的图像和性质例2 [宿迁中考]在平面直角坐标系中, 若直线y=kx+b经过第一、 三、四象限, 则直线y=bx+k不经过的象限是( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限分析 因为直线y=kx+b经过第一、三、四象限, 所以k>0, b<0, 所以 直线y=bx+k经过第一、二、四象限, 所以直线y=bx+k不经过第三象限.C相关题2 已知一次函数y=(6+3m)x+ (n-4).
(1)当m为何值时, y随x的增 大而减小?
(2)当m, n为何值时, 函数 的图像与y轴的交点在x轴 的下方?
(3)当m, n为何值时, 函数 图像经过原点?[解析] (1)当6+3m<0时,y随x的增大而减小;
(2)当6+3m≠0且n-4<0时,函数的图像与y轴的交点在x轴的下方;
(3)当6+3m≠0且n-4=0时,函数图像经过原点.解:(1)当6+3m<0,即m<-2时,y随x的增大而减小.
(2)当6+3m≠0且n-4<0时,函数的图像与y轴的交点在x轴的下方,
解得m≠-2且n<4,
所以当m≠-2且n<4时,函数的图像与y轴的交点在x轴的下方.
(3)当6+3m≠0且n-4=0时,函数图像经过原点,
解得m≠-2且n=4,
所以当m≠-2且n=4时,函数图像经过原点.【要点指导】确定函数表达式的方法:(1)根据基本数量关系列出 函数表达式;(2)根据数学公式列出函数表达式;(3)运用点的坐标列方 程求待定系数确定函数表达式. 在确定实际问题中的函数表达式时, 不 要忽略自变量的取值范围.专题三 确定函数表达式例3 [肇庆中考]已知一次函数y=kx-4, 当x=2时, y= -3.
(1)求一次函数的表达式;
(2)将该函数的图像向上平移6个单位长度, 求平移后的图像与x轴的交点 坐标.解:(1)将x=2, y= -3代入y=kx-4, 得-3=2k-4, 解得k= ,
所以一次函数的表达式为y= x-4.
(2)将y= x-4的图像向上平移6个单位长度得函数y= x+2的图像, 当y=0时, x=-4, 所以平移后的图像与x轴的交点坐标为(-4, 0).相关题3 如图4-Z-3, 直线l过A(0, -1), B(1, 0)两点, 则直线 l所对应的函数表达式为 __________. y=x-1【要点指导】与一次函数有关的计算题一直是中考的热点考题. 它 涉及的计算一般有求直线与坐标轴的交点坐标, 求两直线的交点坐标, 求平面直角坐标系中有关图形的面积、周长及线段的长度等.专题四 与一次函数有关的计算题例4 如图4-Z-4, 在平面直角坐标系xOy中, 一次 函数的图像与x轴交于点A(1, 0), 与y轴交于点B(0, 2), 求 一次函数的表达式及线段AB的长.解: 设一次函数的表达式为y=kx+b(k≠0).
由题意 可知, 点A(1, 0) , B(0, 2)在直线y=kx+b上,
所以b=2, k+b= 0 ,解得b=2, k=-2,
所以一次函数的表达式为 y=-2x+2.
因为OA=1, OB=2, ∠AOB=90°,
所以AB=相关题4 如图4-Z-5, 已知两直线l1 和l2, 直线l1的函数表达式 是y=x+4, 且直线l1与x轴交 于点C, 直线l2经过A(0, 4), B(2, 0)两点.
(1)求点C的坐标;
(2)求直线l2的函数表达式;
(3)求△ABC的面积.【要点指导】以实际问题为载体的一次函数图像问题主要涉及两 个方面:一是根据图像信息求函数表达式, 进而解决实际问题;二是根 据实际问题列出函数表达式, 画出函数图像, 此类问题往往将多个一次函 数的图像放在同一个平面直角坐标系中. 解此类问题的关键在于看懂图 像和熟悉实际情景中的数量关系, 应用数形结合的思想方法, 联系各种知 识进行分析推理, 将图像信息与实际数据转化为相应的数学问题.专题五 一次函数图像信息题例5 为积极响应党中央关于支援地震灾区抗震救灾的号召, 某工厂 日夜连续加班, 计划为灾区生产1000顶帐篷.生产过程中的剩余生产任务 y(顶)与已用生产时间x(时)
之间的关系如图4-Z-6 所示.
(1)求变量y与x之间的函数表达式
(不要求写自变 量的取值范围);
(2)求m的值. 解: (1)设y与x之间的函数表达式为y=kx+1000(k≠0),
由图像知, 点(30, 400)在一次函数y=kx+1000的图像上,
将其代入上述函数表达式, 解得k=-20,
所以y与x之间的函数表达式为y=-20x+1000.
(2)当y=0时, x=50, 所以m的值是50. 相关题5 某种形如长方体(容积为 2000 mL)的盒装果汁, 其 盒底面是边长为10 cm的 正方形, 现从盒中倒出果 汁, 盒中剩余果汁的体积 y(mL)与果汁下降的高度 x(cm)之间的函数关系如图 4-Z-7所示(盒子的厚度 不计).
(1)求出y与x的函数表达式, 并写出自
变量的取值范围; (2)若将满盒果汁倒出一部 分, 下降的高度为15 cm, 剩余的果汁还能够倒满每 个容积为180 mL的三个纸 杯吗?请计算说明.解: (1)设函数表达式为y=kx+b(k≠0),由图像知,
点(0,2000),(20,0)在一次函数y=kx+b的图像上,
将两点的坐标代入上述函数表达式,
解得k=-100,b=2000,所以y=-100x+2000(0≤x≤20).
(2)当x=15时,y=-100×15+2000=500.
因为500<180×3,所以不能倒满三个纸杯.【要点指导】一次函数是解决问题的常见模型, 近几年中考中考查一 次函数的实际应用题越来越多, 此类题目内容新颖, 与生活联系紧密, 解题 的关键是能从实际问题中抽象出一次函数模型, 并求出其函数表达式. 专题六 一次函数的应用例6 某商场欲购进A, B两种品牌的饮料500箱, 这两种饮料每箱的进 价和售价如下表所示. 设购进A种饮料x箱, 且所购进的两种饮料能全部卖 完, 获得的总利润为y元.
(1)求y关于x的函数表达式;
(2)如果购进两种饮料的总费用不超
过20 000元, 那么该商场如何进货 才
能获利最大?并求出最大利润.
(注:利润=售价-进价)解: (1)y=(68-55)x+(40-35)(500-x)=8x+2500,
即y=8x+2500(0<x<500, 且x为整数).
(2)由题意, 得55x+35(500-x)≤20 000,解得x≤125,
即x可取得的最大值 为125. 对于函数y=8x+2500,
因为k=8>0, 所以y随x的增大而增大,
即当x取 最大值时, 函数y也取最大值.
因此, 当x=125时, y最大值=8×125+2500=3500, 500-125=375, 所以该商场购进A, B两种饮料分别为125箱, 375箱时, 才能获利最大, 最大利润为3500元.
500-125=375, 所以该商场购进A, B两种饮料分别为125箱, 375箱时, 才能获利最大, 最大利润为3500元. 相关题6 [陕西中考]小李从西安通 过某快递公司给在南昌 的外婆寄了一盒樱桃, 寄 快递时, 他了解到这个公 司除收取每次6元的包装 费外, 樱桃不超过1 kg收 费22元, 超过1 kg, 则超出 部分按每千克10元加收 费用. 设该公司从西安到 南昌快递樱桃的费用为 y(元), 所寄樱桃为x(kg).
(1)求y与x之间的函数表 达式;
(2)已知小李给外婆寄了 2.5 kg樱桃, 请你求出这次 快递的费用是多少元.[解析] (1)本题是分段函数问题,应该分别列出01两个范围内y与x之间的函数表达式.
(2)因为2.5>1,所以把x=2.5代入当x>1时的函数表达式中求解.【要点指导】一次函数的图像与几何图形相结合的题近年来越来 越多地出现在中考题中, 成为中考试题的一个亮点. 解决此类题有两个技 巧:一是将问题转化为一般的几何问题解决;二是借助平面直角坐标系, 用代数的方法解决几何图形问题, 即利用数形结合思想解决.素养提升专题? 数形结合思想例 [包头中考]如图4-Z-8, 直线y= x+4与x 轴、y轴分别交于点A和点B, C, D分别为线段AB, OB 的中点, P为OA上一动点, PC+PD的值最小时, 点P的 坐标为( ).
A.(-3, 0) B.(-6, 0)
C.(- , 0) D.(- , 0) C分析 作点D关于x轴的对称点D', 连接CD'交x轴于点P,
此时 PC+PD的值最小, 如图4-Z-8所示.
令y= x+4中x=0, 则y=4, 所以点B的坐标为(0, 4).
令y= x+4中y=0, 则 x+4=0, 解得x=-6,
所以 点A的坐标为(-6, 0).
因为C, D分别为线段AB, OB的中点,
所以点C的 坐标为(-3, 2), 点D的坐标为(0, 2).
因为点D'和点D关于x轴对称, 所 以点D'的坐标为(0, -2). 设直线CD'的函数表达式为y=kx+b(k≠0).
因为直线CD'过点C(-3, 2), D'(0, -2),
所以b= -2①, -3 k+b= 2②, 把①代入②, 得k= - ,
所以直线CD'的函数表达式为y= - x-2.
令y= - x-2中y=0, 则0= - x-2, 解得x= - ,
所以点P的坐标为(- , 0). 故选C. 相关题 如图4 - Z - 9 , 一次函数 y= - x+2的图像分别与 x轴, y轴交于点A, B, 以线 段AB为边在第一象限内 作等腰直角三角形ABC , ∠BAC=90°. 求过B, C两 点直线的函数表达式.中考链接母题1 (教材P116习题4.1A组第4题)
甲、乙两人在一次跨栏比赛中, 路程s(m)与 时间t(s)的函数关系如图4-Z-10所示, 回答下列 问题:
(1)这次比赛的赛程是多少?
(2)甲、乙二人谁先到达终点?
(3)求乙在这次比赛中的平均速度.考点:从函数图像上获取信息.
考情:从函数的图像上获取信息是常见的考题, 主要考查学生对函数图像上点的意义、图像的变 化趋势的理解以及对数形结合思想的运用.
策略:正确理解平面直角坐标系中横轴、纵轴所 表示的意义及平行于x轴的线段与x轴、y轴的交 点的含义.链接1 [咸宁中考]甲、乙两人在笔直的湖边 公路上同起点、同终点、同方向匀速步行2400米, 先到终点的人原地休息. 已知甲先出发4分钟, 在 整个步行过程中,
甲、乙两人的距离y(米)与甲出 发
的时间t(分)之间的关系如图4-Z-11
所示, 下列 结论: ①甲步行的速度为
60米/分; ②乙走完全程用了32分钟;③乙用16分钟追上甲; ④乙到达终点时, 甲离终点还有300米. 其中正确的结论有( ).
A.1个 B.2个
C.3个 D.4个[答案] A分析 由图可得: 甲步行的速度为240÷4=60(米/分), 故①正确.
乙走完全程用的时间为2400÷(16×60÷12)= 30(分), 故②错误.
乙追上甲用的时间为16-4=12(分), 故③错误.
乙到达终点时, 甲离终点的距离是2400- (4+30)×60=360(米), 故④错误.
故选A. 母题2 (教材P128习题4.3B组第6题)
正比例函数y=kx(k≠0)的函数值 y随 x的增大 而增大, 则一次函数y=x+k的图像大致是( ).图4-Z-12考点:一次函数的图像与性质.
考情:此类题比较简单, 一般以选择题、填空题 的形式出现.策略:k, b的符号与函数图像、性质的关系 如下:链接2 [湘潭中考]若b>0, 则一次函数y= -x+b的图像大致是( ).C图4-Z-13分析 ∵一次函数y=-x+b中, k=-1<0, b>0,
∴一次函数y=-x+b的图像经过第一、二、四 象限. 故选C链接3 [常德中考]若一次函数y=(k-2)x+1的 函数值y随x的增大而增大, 则( ).
A.k<2 B.k>2
C.k>0 D.k<0B分析 由题意, 得k-2>0, 解得k>2. 故选B.链接4 [眉山中考]已知点A(x1, y1), B(x2, y2)在 直线y=kx+b上, 且直线经过第一、二、四象限, 当 x1<x2时, y1与y2的大小关系为________. (用“>” 连接)y1>y2分析 ∵直线经过第一、二、四象限, ∴y随x的增大而减小.
∵x1<x2, ∴y1与y2的大小关系为y1>y2.母题3 (教材P127练习第1题(1))
将直线y = 3x向下平移2个单位,得到直线 ________.考点:一次函数图像(直线)的平移.
考情:一次函数图像的平移在中考中常以选择题 填空题的形式出现,难度不大, 但是要弄清楚上下平 移时图像与y轴交点坐标的变化规律.策略:一次函数图像的平移规律:左加右减自变量, 上加下减常数项.
①将一次函数y=kx+b 的图像向上或向下平移m个单位(其中m>0),得 到的图像对应的函数表达式为y=k x+(b+m)或 y=kx+(b-m).
②将一次函数y=kx+b的图像向左 或向右平移n个单位(其中n>0), 得到的图像对应的函数表达式为y=k(x+n)+b或y=k(x-n)+b.链接5 [娄底中考]将直线y=2x-3向右平移2 个单位长度, 再向上平移3个单位长度后, 所得的直 线的函数表达式为( ).
A.y=2x-4 B.y=2x+4
C.y=2x+2 D.y=2x-2A分析 平移后所得直线的函数表达式为y= 2(x-2)-3+3=2x-4. 故选A.母题4 (教材P131练习第2题)
已知一次函数的图像经过两点A ( - 1,3 ) , B(2,-5), 求这个函数的表达式.考点:待定系数法求函数表达式.
考情:待定系数法求函数表达式是利用函数模型 解决实际问题的工具, 是最常考的题型, 必须牢记 解题方法.
策略:在已知条件中找两个已知点的坐标(或两 对x, y的值)代入y=kx+b中列方程组求出k, b的值, 为确保计算正确, 求出k, b的值后应代入每个方程 检验.链接6 [湖州中考]已知y是x的一次函数, 当 x=3时, y=1;当x=-2时, y=-4. 求这个一次函数的 表达式.母题5 (教材P134练习第2题)
某移动公司对于移动话费推出两种收费 方式:
A方案:每月收取基本月租费25元, 另收通话 费为0.36元/min;
B方案:零月租费, 通话费为0.5元/min.
(1)试写出A, B两种方案所付话费y(元)与通话 时间t(min)之间的函数表达式;
(2)分别画出这两个函数的图像;
(3)若林先生每月通话300 min, 他选择哪种付 费方式比较合算?考点:应用函数模型解决具体问题.
考情:中考中注重考查学生运用数学知识解决实 际问题的能力, 而建立函数模型解决问题是最常 见的考查方式, 极其重要.
策略:先根据条件求出函数表达式, 再利用函数 表达式求出特定x(y)条件下y(x)的值或取值范围, 从而解决实际问题.链接7 [永州中考]永州市是一个降水丰富的 地区, 今年4月初, 某地连续降雨导致该地某水库水 位持续上涨, 下表是该水库4月1日~4月4日的水位 变化情况:
(1)请建立该水库水位y与日期x之间的函数 模型;
(2)请用求出的函数表达式预测该水库今年 4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年 12月1日的水位吗?(2)当x=6时, y=0.5×6+19.5=22.50.
答:预测该水库今年4月6日的水位为22.50米.
(3)不能, 因为用所建立的函数模型远离已知 数据做预测是不可靠的.
谢 谢 观 看!
A.第一象限 B.第二象限
C.第三象限 D.第四象限分析 因为直线y=kx+b经过第一、三、四象限, 所以k>0, b<0, 所以 直线y=bx+k经过第一、二、四象限, 所以直线y=bx+k不经过第三象限.C相关题2 已知一次函数y=(6+3m)x+ (n-4).
(1)当m为何值时, y随x的增 大而减小?
(2)当m, n为何值时, 函数 的图像与y轴的交点在x轴 的下方?
(3)当m, n为何值时, 函数 图像经过原点?[解析] (1)当6+3m<0时,y随x的增大而减小;
(2)当6+3m≠0且n-4<0时,函数的图像与y轴的交点在x轴的下方;
(3)当6+3m≠0且n-4=0时,函数图像经过原点.解:(1)当6+3m<0,即m<-2时,y随x的增大而减小.
(2)当6+3m≠0且n-4<0时,函数的图像与y轴的交点在x轴的下方,
解得m≠-2且n<4,
所以当m≠-2且n<4时,函数的图像与y轴的交点在x轴的下方.
(3)当6+3m≠0且n-4=0时,函数图像经过原点,
解得m≠-2且n=4,
所以当m≠-2且n=4时,函数图像经过原点.【要点指导】确定函数表达式的方法:(1)根据基本数量关系列出 函数表达式;(2)根据数学公式列出函数表达式;(3)运用点的坐标列方 程求待定系数确定函数表达式. 在确定实际问题中的函数表达式时, 不 要忽略自变量的取值范围.专题三 确定函数表达式例3 [肇庆中考]已知一次函数y=kx-4, 当x=2时, y= -3.
(1)求一次函数的表达式;
(2)将该函数的图像向上平移6个单位长度, 求平移后的图像与x轴的交点 坐标.解:(1)将x=2, y= -3代入y=kx-4, 得-3=2k-4, 解得k= ,
所以一次函数的表达式为y= x-4.
(2)将y= x-4的图像向上平移6个单位长度得函数y= x+2的图像, 当y=0时, x=-4, 所以平移后的图像与x轴的交点坐标为(-4, 0).相关题3 如图4-Z-3, 直线l过A(0, -1), B(1, 0)两点, 则直线 l所对应的函数表达式为 __________. y=x-1【要点指导】与一次函数有关的计算题一直是中考的热点考题. 它 涉及的计算一般有求直线与坐标轴的交点坐标, 求两直线的交点坐标, 求平面直角坐标系中有关图形的面积、周长及线段的长度等.专题四 与一次函数有关的计算题例4 如图4-Z-4, 在平面直角坐标系xOy中, 一次 函数的图像与x轴交于点A(1, 0), 与y轴交于点B(0, 2), 求 一次函数的表达式及线段AB的长.解: 设一次函数的表达式为y=kx+b(k≠0).
由题意 可知, 点A(1, 0) , B(0, 2)在直线y=kx+b上,
所以b=2, k+b= 0 ,解得b=2, k=-2,
所以一次函数的表达式为 y=-2x+2.
因为OA=1, OB=2, ∠AOB=90°,
所以AB=相关题4 如图4-Z-5, 已知两直线l1 和l2, 直线l1的函数表达式 是y=x+4, 且直线l1与x轴交 于点C, 直线l2经过A(0, 4), B(2, 0)两点.
(1)求点C的坐标;
(2)求直线l2的函数表达式;
(3)求△ABC的面积.【要点指导】以实际问题为载体的一次函数图像问题主要涉及两 个方面:一是根据图像信息求函数表达式, 进而解决实际问题;二是根 据实际问题列出函数表达式, 画出函数图像, 此类问题往往将多个一次函 数的图像放在同一个平面直角坐标系中. 解此类问题的关键在于看懂图 像和熟悉实际情景中的数量关系, 应用数形结合的思想方法, 联系各种知 识进行分析推理, 将图像信息与实际数据转化为相应的数学问题.专题五 一次函数图像信息题例5 为积极响应党中央关于支援地震灾区抗震救灾的号召, 某工厂 日夜连续加班, 计划为灾区生产1000顶帐篷.生产过程中的剩余生产任务 y(顶)与已用生产时间x(时)
之间的关系如图4-Z-6 所示.
(1)求变量y与x之间的函数表达式
(不要求写自变 量的取值范围);
(2)求m的值. 解: (1)设y与x之间的函数表达式为y=kx+1000(k≠0),
由图像知, 点(30, 400)在一次函数y=kx+1000的图像上,
将其代入上述函数表达式, 解得k=-20,
所以y与x之间的函数表达式为y=-20x+1000.
(2)当y=0时, x=50, 所以m的值是50. 相关题5 某种形如长方体(容积为 2000 mL)的盒装果汁, 其 盒底面是边长为10 cm的 正方形, 现从盒中倒出果 汁, 盒中剩余果汁的体积 y(mL)与果汁下降的高度 x(cm)之间的函数关系如图 4-Z-7所示(盒子的厚度 不计).
(1)求出y与x的函数表达式, 并写出自
变量的取值范围; (2)若将满盒果汁倒出一部 分, 下降的高度为15 cm, 剩余的果汁还能够倒满每 个容积为180 mL的三个纸 杯吗?请计算说明.解: (1)设函数表达式为y=kx+b(k≠0),由图像知,
点(0,2000),(20,0)在一次函数y=kx+b的图像上,
将两点的坐标代入上述函数表达式,
解得k=-100,b=2000,所以y=-100x+2000(0≤x≤20).
(2)当x=15时,y=-100×15+2000=500.
因为500<180×3,所以不能倒满三个纸杯.【要点指导】一次函数是解决问题的常见模型, 近几年中考中考查一 次函数的实际应用题越来越多, 此类题目内容新颖, 与生活联系紧密, 解题 的关键是能从实际问题中抽象出一次函数模型, 并求出其函数表达式. 专题六 一次函数的应用例6 某商场欲购进A, B两种品牌的饮料500箱, 这两种饮料每箱的进 价和售价如下表所示. 设购进A种饮料x箱, 且所购进的两种饮料能全部卖 完, 获得的总利润为y元.
(1)求y关于x的函数表达式;
(2)如果购进两种饮料的总费用不超
过20 000元, 那么该商场如何进货 才
能获利最大?并求出最大利润.
(注:利润=售价-进价)解: (1)y=(68-55)x+(40-35)(500-x)=8x+2500,
即y=8x+2500(0<x<500, 且x为整数).
(2)由题意, 得55x+35(500-x)≤20 000,解得x≤125,
即x可取得的最大值 为125. 对于函数y=8x+2500,
因为k=8>0, 所以y随x的增大而增大,
即当x取 最大值时, 函数y也取最大值.
因此, 当x=125时, y最大值=8×125+2500=3500, 500-125=375, 所以该商场购进A, B两种饮料分别为125箱, 375箱时, 才能获利最大, 最大利润为3500元.
500-125=375, 所以该商场购进A, B两种饮料分别为125箱, 375箱时, 才能获利最大, 最大利润为3500元. 相关题6 [陕西中考]小李从西安通 过某快递公司给在南昌 的外婆寄了一盒樱桃, 寄 快递时, 他了解到这个公 司除收取每次6元的包装 费外, 樱桃不超过1 kg收 费22元, 超过1 kg, 则超出 部分按每千克10元加收 费用. 设该公司从西安到 南昌快递樱桃的费用为 y(元), 所寄樱桃为x(kg).
(1)求y与x之间的函数表 达式;
(2)已知小李给外婆寄了 2.5 kg樱桃, 请你求出这次 快递的费用是多少元.[解析] (1)本题是分段函数问题,应该分别列出0
(2)因为2.5>1,所以把x=2.5代入当x>1时的函数表达式中求解.【要点指导】一次函数的图像与几何图形相结合的题近年来越来 越多地出现在中考题中, 成为中考试题的一个亮点. 解决此类题有两个技 巧:一是将问题转化为一般的几何问题解决;二是借助平面直角坐标系, 用代数的方法解决几何图形问题, 即利用数形结合思想解决.素养提升专题? 数形结合思想例 [包头中考]如图4-Z-8, 直线y= x+4与x 轴、y轴分别交于点A和点B, C, D分别为线段AB, OB 的中点, P为OA上一动点, PC+PD的值最小时, 点P的 坐标为( ).
A.(-3, 0) B.(-6, 0)
C.(- , 0) D.(- , 0) C分析 作点D关于x轴的对称点D', 连接CD'交x轴于点P,
此时 PC+PD的值最小, 如图4-Z-8所示.
令y= x+4中x=0, 则y=4, 所以点B的坐标为(0, 4).
令y= x+4中y=0, 则 x+4=0, 解得x=-6,
所以 点A的坐标为(-6, 0).
因为C, D分别为线段AB, OB的中点,
所以点C的 坐标为(-3, 2), 点D的坐标为(0, 2).
因为点D'和点D关于x轴对称, 所 以点D'的坐标为(0, -2). 设直线CD'的函数表达式为y=kx+b(k≠0).
因为直线CD'过点C(-3, 2), D'(0, -2),
所以b= -2①, -3 k+b= 2②, 把①代入②, 得k= - ,
所以直线CD'的函数表达式为y= - x-2.
令y= - x-2中y=0, 则0= - x-2, 解得x= - ,
所以点P的坐标为(- , 0). 故选C. 相关题 如图4 - Z - 9 , 一次函数 y= - x+2的图像分别与 x轴, y轴交于点A, B, 以线 段AB为边在第一象限内 作等腰直角三角形ABC , ∠BAC=90°. 求过B, C两 点直线的函数表达式.中考链接母题1 (教材P116习题4.1A组第4题)
甲、乙两人在一次跨栏比赛中, 路程s(m)与 时间t(s)的函数关系如图4-Z-10所示, 回答下列 问题:
(1)这次比赛的赛程是多少?
(2)甲、乙二人谁先到达终点?
(3)求乙在这次比赛中的平均速度.考点:从函数图像上获取信息.
考情:从函数的图像上获取信息是常见的考题, 主要考查学生对函数图像上点的意义、图像的变 化趋势的理解以及对数形结合思想的运用.
策略:正确理解平面直角坐标系中横轴、纵轴所 表示的意义及平行于x轴的线段与x轴、y轴的交 点的含义.链接1 [咸宁中考]甲、乙两人在笔直的湖边 公路上同起点、同终点、同方向匀速步行2400米, 先到终点的人原地休息. 已知甲先出发4分钟, 在 整个步行过程中,
甲、乙两人的距离y(米)与甲出 发
的时间t(分)之间的关系如图4-Z-11
所示, 下列 结论: ①甲步行的速度为
60米/分; ②乙走完全程用了32分钟;③乙用16分钟追上甲; ④乙到达终点时, 甲离终点还有300米. 其中正确的结论有( ).
A.1个 B.2个
C.3个 D.4个[答案] A分析 由图可得: 甲步行的速度为240÷4=60(米/分), 故①正确.
乙走完全程用的时间为2400÷(16×60÷12)= 30(分), 故②错误.
乙追上甲用的时间为16-4=12(分), 故③错误.
乙到达终点时, 甲离终点的距离是2400- (4+30)×60=360(米), 故④错误.
故选A. 母题2 (教材P128习题4.3B组第6题)
正比例函数y=kx(k≠0)的函数值 y随 x的增大 而增大, 则一次函数y=x+k的图像大致是( ).图4-Z-12考点:一次函数的图像与性质.
考情:此类题比较简单, 一般以选择题、填空题 的形式出现.策略:k, b的符号与函数图像、性质的关系 如下:链接2 [湘潭中考]若b>0, 则一次函数y= -x+b的图像大致是( ).C图4-Z-13分析 ∵一次函数y=-x+b中, k=-1<0, b>0,
∴一次函数y=-x+b的图像经过第一、二、四 象限. 故选C链接3 [常德中考]若一次函数y=(k-2)x+1的 函数值y随x的增大而增大, 则( ).
A.k<2 B.k>2
C.k>0 D.k<0B分析 由题意, 得k-2>0, 解得k>2. 故选B.链接4 [眉山中考]已知点A(x1, y1), B(x2, y2)在 直线y=kx+b上, 且直线经过第一、二、四象限, 当 x1<x2时, y1与y2的大小关系为________. (用“>” 连接)y1>y2分析 ∵直线经过第一、二、四象限, ∴y随x的增大而减小.
∵x1<x2, ∴y1与y2的大小关系为y1>y2.母题3 (教材P127练习第1题(1))
将直线y = 3x向下平移2个单位,得到直线 ________.考点:一次函数图像(直线)的平移.
考情:一次函数图像的平移在中考中常以选择题 填空题的形式出现,难度不大, 但是要弄清楚上下平 移时图像与y轴交点坐标的变化规律.策略:一次函数图像的平移规律:左加右减自变量, 上加下减常数项.
①将一次函数y=kx+b 的图像向上或向下平移m个单位(其中m>0),得 到的图像对应的函数表达式为y=k x+(b+m)或 y=kx+(b-m).
②将一次函数y=kx+b的图像向左 或向右平移n个单位(其中n>0), 得到的图像对应的函数表达式为y=k(x+n)+b或y=k(x-n)+b.链接5 [娄底中考]将直线y=2x-3向右平移2 个单位长度, 再向上平移3个单位长度后, 所得的直 线的函数表达式为( ).
A.y=2x-4 B.y=2x+4
C.y=2x+2 D.y=2x-2A分析 平移后所得直线的函数表达式为y= 2(x-2)-3+3=2x-4. 故选A.母题4 (教材P131练习第2题)
已知一次函数的图像经过两点A ( - 1,3 ) , B(2,-5), 求这个函数的表达式.考点:待定系数法求函数表达式.
考情:待定系数法求函数表达式是利用函数模型 解决实际问题的工具, 是最常考的题型, 必须牢记 解题方法.
策略:在已知条件中找两个已知点的坐标(或两 对x, y的值)代入y=kx+b中列方程组求出k, b的值, 为确保计算正确, 求出k, b的值后应代入每个方程 检验.链接6 [湖州中考]已知y是x的一次函数, 当 x=3时, y=1;当x=-2时, y=-4. 求这个一次函数的 表达式.母题5 (教材P134练习第2题)
某移动公司对于移动话费推出两种收费 方式:
A方案:每月收取基本月租费25元, 另收通话 费为0.36元/min;
B方案:零月租费, 通话费为0.5元/min.
(1)试写出A, B两种方案所付话费y(元)与通话 时间t(min)之间的函数表达式;
(2)分别画出这两个函数的图像;
(3)若林先生每月通话300 min, 他选择哪种付 费方式比较合算?考点:应用函数模型解决具体问题.
考情:中考中注重考查学生运用数学知识解决实 际问题的能力, 而建立函数模型解决问题是最常 见的考查方式, 极其重要.
策略:先根据条件求出函数表达式, 再利用函数 表达式求出特定x(y)条件下y(x)的值或取值范围, 从而解决实际问题.链接7 [永州中考]永州市是一个降水丰富的 地区, 今年4月初, 某地连续降雨导致该地某水库水 位持续上涨, 下表是该水库4月1日~4月4日的水位 变化情况:
(1)请建立该水库水位y与日期x之间的函数 模型;
(2)请用求出的函数表达式预测该水库今年 4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年 12月1日的水位吗?(2)当x=6时, y=0.5×6+19.5=22.50.
答:预测该水库今年4月6日的水位为22.50米.
(3)不能, 因为用所建立的函数模型远离已知 数据做预测是不可靠的.
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
