湘教版数学八年级下册第5章 数据的频数分布章末复习课件(50张PPT)
文档属性
| 名称 | 湘教版数学八年级下册第5章 数据的频数分布章末复习课件(50张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 959.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-07 00:00:00 | ||
图片预览








文档简介
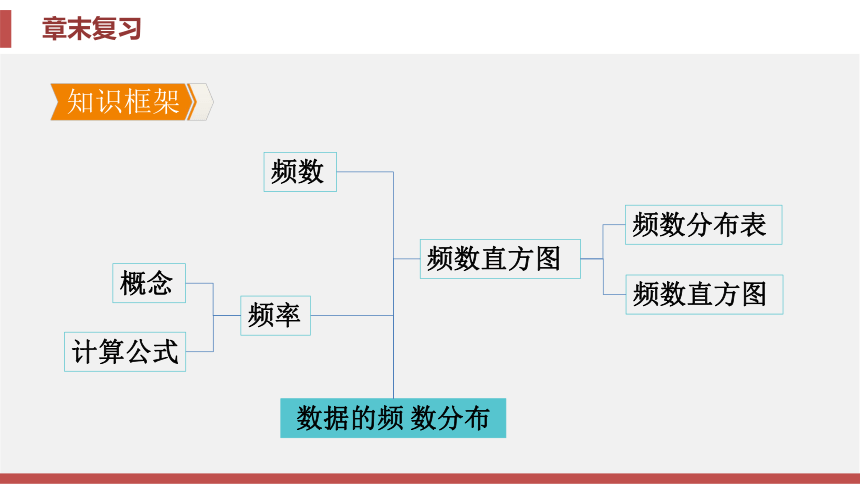
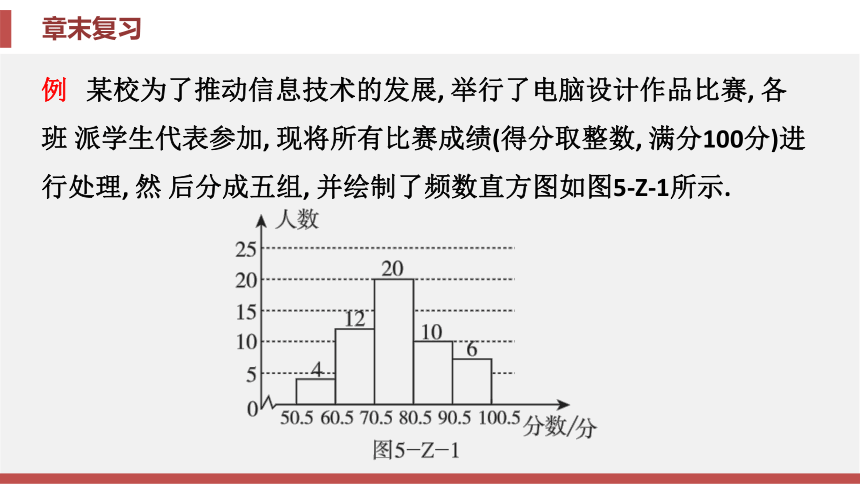
课件50张PPT。第5章 数据的频数分布章末复习第5章 数据的频数分布章末复习知识框架归纳整合素养提升中考链接知识框架【要点指导】频数、频率及频数直方图常常结合在一起考查, 准确 理解它们的意义才能正确解题.归纳整合专题 频数、频率及频数直方图的应用例 某校为了推动信息技术的发展, 举行了电脑设计作品比赛, 各班 派学生代表参加, 现将所有比赛成绩(得分取整数, 满分100分)进行处理, 然 后分成五组, 并绘制了频数直方图如图5-Z-1所示. 请结合图中所提供的信息, 解答下列问题:
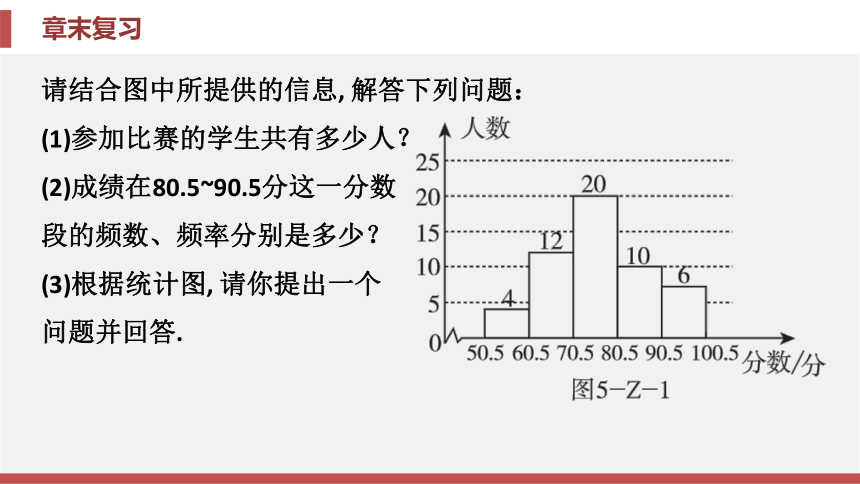
(1)参加比赛的学生共有多少人?
(2)成绩在80.5~90.5分这一分数
段的频数、频率分别是多少?
(3)根据统计图, 请你提出一个
问题并回答.解:(1)参加比赛的学生共有4+12+20+10+6=52(人).
(2)成绩在80.5~90.5分这一分数段的频数为10, 频率为 .
(3)答案不唯一, 如:
成绩在90.5~100.5分这一分数段的学生有多少人?
答:成绩在90.5~100.5分这一分数段的学生有6人. 相关题 如图5-Z-2所示, 纵轴表 示八年级(1)班学生的人 数, 横轴表示学生的身高, 根据频数直方图提供的信 息, 回答下列问题:
(1)八年级(1)班共有学生 多少人?
(2)身高在160.5~170.5 cm 这一范
围内的学生有多 少人?这一组
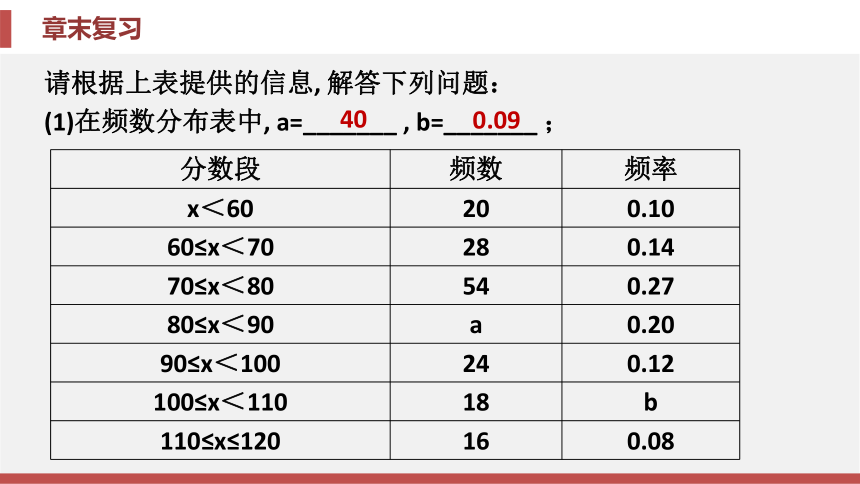
的频率是 多少?【要点指导】通过观察“图形”的特征、规律和变化趋势, 分离出 “数”的特征、规律和变化趋势, 并解决相应的问题. 素养提升专题 数形结合思想例 某课题组为了解全市八年级学生对数学知识的掌握情况, 在一 次数学检测中, 从全市24 000名八年级考生中随机抽取部分学生的数学成 绩进行调查, 并将调查结果绘制成下表:请根据上表提供的信息, 解答下列问题:
(1)在频数分布表中, a=_______ , b=_______ ; 400.09(2)请补全如图5-Z-3所示的频数直方图;(3)如果把成绩在90分以上(含90分)定为优秀, 那么该市八年级考生中 数学成绩为优秀的学生所占的百分比是多少?解:(2)补全频数直方图如图5-Z-4所示.
(3)0.12+0.09+0.08=0.29,
0.29×100%=29%.
答:该市八年级考生中数
学成绩为优秀的学生所占
的百分比为29%. 相关题 某校八年级共有学生900人, 为了解这个年级学生的体能 情况, 从中随机抽取部分学 生进行1分钟跳绳测试, 并指 定甲、乙、丙、丁四名同学对 这次测试结果的数据做出整 理. 下面是这四名同学提供 的部分信息.
甲:将全体测试数据分成 6组,绘
制成如图5-Z-5 所示的频数直方图;乙:跳绳次数不少于105 次的同学所占的比例为 96%;
丙:第①②两组的频率之 和为0.12, 且第②组与第⑥ 组的频数都是12;
丁:第②③④组的频数之 比是
4∶17∶15. 根据这四名同学提供
的信 息, 请解答下列问题: (1)这次跳绳测试共抽取了 多少名学生?各组分别有多 少人?
(2)如果跳绳次数不少于135 为优秀, 那么根据这次抽查 的结果, 计算全年级跳绳达 到优秀的人数所占的百分比.中考链接母题1 (教材P153习题5.1A组第2题)
如图5-Z-6为一个转盘, 让转盘自由转动18
次, 记录每次指针指向区域的颜色如下:
请制作反映指针指向
区域颜色的频数分布
表, 并计算相应的频率. 黄 红 绿 绿 红 黄 绿 红 红
黄 绿 红 黄 红 绿 绿 黄 黄考点:频率的概念及计算公式.
考情:频数、频率的概念是中考中常考的知识点, 常给所考知识点添加一个背景情境, 着重考查频 率计算公式的灵活运用.
策略:先列出公式, 再将已知条件代入公式求解. 链接1 [常德中考]某校对七年级全体学生 进行了一次视力普查, 得到如下统计表, 则视力在 4.9≤x<5.5这个范围的频率为_______.0.35分析 视力在4.9≤x<5.5这个范围的频数为 60+10=70,
则视力在4.9≤x<5.5这个范围的频率为
故答案为0.35. 母题2 (教材P153习题5.1A组第1题)
某中学八年级(2)班40名同学投票选举班长, 候选人包括陈佳、彭晓、黄敏和汤伟四位. 为了方 便记录, 他们的得票分别以C, P, H, T来代表, 投票 结果如下:
P P H C C C T H P T
T P H T C C T P P H
T H P C P H H T T C
T T C H P P T H T P(1)请根据上述投票结果完成下表:
(2)如果得票最高的候选人被选为班长, 则四 人中哪一位会当选?考点:频数与频率的实际应用.
考情:考情:利用频数与频率的知识解决合理设计方案 或选择方案等问题.
策略:依据频数与频率的关系, 按试验结果中各对 象的频数之比设计方案. 链接2 [临沂中考] 某地某月1~20日中午12 时的气温(单位:℃)如下:
22 31 25 15 18 23 21 20 27 17
20 12 18 21 21 16 20 24 26 19(1)将下列频数分布表补充完整:(2)补全频数直方图;
(3)根据频数分布表或频数直方图, 分析数据 的分布情况. 解:(1)补充表格如下:(2)补全频数直方图如图5-Z-7.
(3)答案不唯一, 如由频数直方图知气温在 17≤x<22内的天数最多.母题3 (教材P159习题5.2A组第1题)
李老师为了了解本班学生的作息时间, 调查班 上50名学生上学路上花费的时间, 他发现学生所花 时间
都少于50 min, 然后将调查数据整理,
作出如 图5-Z-8所示的频数直方图的
一部分.
(1)补全频数直方图;(2)该班学生在路上花费的时间在哪个范围内 最多?
(3)该班学生上学路上花费时间在30 min以上 (含30 min)的人数占全班人数的百分比是多少?考点:频数直方图.
考情:中考中常将统计表与统计图结合起来考查 灵活运用统计知识的能力.
策略:当统计表(或统计图)中某些内容不完整时, 应 从其他图表中获取这些未知内容的信息, 然后运用 频数、频率知识进行计算, 补全图表中缺少的内容, 进而根据补全的内容解决其他实际问题. 链接3 [娄底中考]根据频数分布表或频数直 方图求加权平均数时, 统计中常用各组的组中值代 表各组的实际数据, 把各组的频数看作相应组中值 的权, 请你依据以上知识, 解决下面的实际问题.
为了解5路公共汽车的运营情况, 公交部门统 计了某天5路公共汽车每个运行班次的载客量, 并 按载客量的多少分成A, B, C, D四组, 得到如下统 计图:(1)求A组对应扇形圆心角的度数,并写出这 天载客量的中位数所在的组;(2)求这天5路公共汽车平均每班次的载客量;(3)如果一个月按30天计算,请估计5路公共 汽车一个月的总载客量,并把结果用科学记数法 表示出来.分析 (1)利用360°乘A组所占的比例即可;
(2)首先计算出各组的组中值,然后再利用加权平 均数公式计算平均数;
(3)利用平均每班次的载客 量×天数×次数可得一个月的总载客量.解: (1)由运营情况频数直方图可知共运营 10+16+18+6=50(次).
A组对应扇形圆心角的度数 为360°× =72°.
这天载客量的中位数在B组.
(2)各组组中值分别如下:A, 10;B, 30;C, 50;D, 70.
答:这天5路公共汽车平均每班次的载客量是 38人. (3)38×50×30=57 000=5.7×104 (人).
答:估计5路公共汽车一个月的总载客量为 5.7×104 人.链接4 [酒泉中考] 中华文明, 源远流长, 中华 汉字, 寓意深广. 为传承中华优秀文化, 某校团委组 织了一次全校3000名学生参加的“汉字听写”大 赛. 为了解本次大赛的成绩, 校团委随机抽取了其中 200名学生的成绩(成绩x取整数, 总分100分)作为样 本进行统计, 制成如下不完整的统计图表:根据所给信息, 解答下列问题:
(1)m=_______,n=_______;
频数、频率分布表(2)补全频数直方图;
频数、频率分布表(3)这200名学生成绩的中位数会落在哪个分 数段?
频数、频率分布表(4)若成绩在90分以上(包括90分)为“优”等, 请你估计该校参加本次比赛的3000名学生中成绩 是“优”等的约有多少人?
频数、频率分布表解: (1)由题可知总数为200,
则10+30+40+ m+50=200, 解得m=70;
由频率总和为1, 得0.05+0.15+n+0.35+0.25= 1, 解得n=0.20.(2)补全的频数直方图如下所示:(3)200个数据的中位数为第100个和第101个 数据的平均数, 由频数、频率分布表, 可得第100个 和第101个数据均位于80≤x<90分数段,则这200 名学生成绩的中位数会落在80≤x<90分数段.
(4)由补全的频数直方图可知在随机抽取的 200个样本中,
成绩在90分以上(包括90分)的频率= =0.25, 3000×0.25=750(人).
答:估计该校参加本次比赛的3000名学生中 成绩是“优”等的人数约为750人.
谢 谢 观 看!
(1)参加比赛的学生共有多少人?
(2)成绩在80.5~90.5分这一分数
段的频数、频率分别是多少?
(3)根据统计图, 请你提出一个
问题并回答.解:(1)参加比赛的学生共有4+12+20+10+6=52(人).
(2)成绩在80.5~90.5分这一分数段的频数为10, 频率为 .
(3)答案不唯一, 如:
成绩在90.5~100.5分这一分数段的学生有多少人?
答:成绩在90.5~100.5分这一分数段的学生有6人. 相关题 如图5-Z-2所示, 纵轴表 示八年级(1)班学生的人 数, 横轴表示学生的身高, 根据频数直方图提供的信 息, 回答下列问题:
(1)八年级(1)班共有学生 多少人?
(2)身高在160.5~170.5 cm 这一范
围内的学生有多 少人?这一组
的频率是 多少?【要点指导】通过观察“图形”的特征、规律和变化趋势, 分离出 “数”的特征、规律和变化趋势, 并解决相应的问题. 素养提升专题 数形结合思想例 某课题组为了解全市八年级学生对数学知识的掌握情况, 在一 次数学检测中, 从全市24 000名八年级考生中随机抽取部分学生的数学成 绩进行调查, 并将调查结果绘制成下表:请根据上表提供的信息, 解答下列问题:
(1)在频数分布表中, a=_______ , b=_______ ; 400.09(2)请补全如图5-Z-3所示的频数直方图;(3)如果把成绩在90分以上(含90分)定为优秀, 那么该市八年级考生中 数学成绩为优秀的学生所占的百分比是多少?解:(2)补全频数直方图如图5-Z-4所示.
(3)0.12+0.09+0.08=0.29,
0.29×100%=29%.
答:该市八年级考生中数
学成绩为优秀的学生所占
的百分比为29%. 相关题 某校八年级共有学生900人, 为了解这个年级学生的体能 情况, 从中随机抽取部分学 生进行1分钟跳绳测试, 并指 定甲、乙、丙、丁四名同学对 这次测试结果的数据做出整 理. 下面是这四名同学提供 的部分信息.
甲:将全体测试数据分成 6组,绘
制成如图5-Z-5 所示的频数直方图;乙:跳绳次数不少于105 次的同学所占的比例为 96%;
丙:第①②两组的频率之 和为0.12, 且第②组与第⑥ 组的频数都是12;
丁:第②③④组的频数之 比是
4∶17∶15. 根据这四名同学提供
的信 息, 请解答下列问题: (1)这次跳绳测试共抽取了 多少名学生?各组分别有多 少人?
(2)如果跳绳次数不少于135 为优秀, 那么根据这次抽查 的结果, 计算全年级跳绳达 到优秀的人数所占的百分比.中考链接母题1 (教材P153习题5.1A组第2题)
如图5-Z-6为一个转盘, 让转盘自由转动18
次, 记录每次指针指向区域的颜色如下:
请制作反映指针指向
区域颜色的频数分布
表, 并计算相应的频率. 黄 红 绿 绿 红 黄 绿 红 红
黄 绿 红 黄 红 绿 绿 黄 黄考点:频率的概念及计算公式.
考情:频数、频率的概念是中考中常考的知识点, 常给所考知识点添加一个背景情境, 着重考查频 率计算公式的灵活运用.
策略:先列出公式, 再将已知条件代入公式求解. 链接1 [常德中考]某校对七年级全体学生 进行了一次视力普查, 得到如下统计表, 则视力在 4.9≤x<5.5这个范围的频率为_______.0.35分析 视力在4.9≤x<5.5这个范围的频数为 60+10=70,
则视力在4.9≤x<5.5这个范围的频率为
故答案为0.35. 母题2 (教材P153习题5.1A组第1题)
某中学八年级(2)班40名同学投票选举班长, 候选人包括陈佳、彭晓、黄敏和汤伟四位. 为了方 便记录, 他们的得票分别以C, P, H, T来代表, 投票 结果如下:
P P H C C C T H P T
T P H T C C T P P H
T H P C P H H T T C
T T C H P P T H T P(1)请根据上述投票结果完成下表:
(2)如果得票最高的候选人被选为班长, 则四 人中哪一位会当选?考点:频数与频率的实际应用.
考情:考情:利用频数与频率的知识解决合理设计方案 或选择方案等问题.
策略:依据频数与频率的关系, 按试验结果中各对 象的频数之比设计方案. 链接2 [临沂中考] 某地某月1~20日中午12 时的气温(单位:℃)如下:
22 31 25 15 18 23 21 20 27 17
20 12 18 21 21 16 20 24 26 19(1)将下列频数分布表补充完整:(2)补全频数直方图;
(3)根据频数分布表或频数直方图, 分析数据 的分布情况. 解:(1)补充表格如下:(2)补全频数直方图如图5-Z-7.
(3)答案不唯一, 如由频数直方图知气温在 17≤x<22内的天数最多.母题3 (教材P159习题5.2A组第1题)
李老师为了了解本班学生的作息时间, 调查班 上50名学生上学路上花费的时间, 他发现学生所花 时间
都少于50 min, 然后将调查数据整理,
作出如 图5-Z-8所示的频数直方图的
一部分.
(1)补全频数直方图;(2)该班学生在路上花费的时间在哪个范围内 最多?
(3)该班学生上学路上花费时间在30 min以上 (含30 min)的人数占全班人数的百分比是多少?考点:频数直方图.
考情:中考中常将统计表与统计图结合起来考查 灵活运用统计知识的能力.
策略:当统计表(或统计图)中某些内容不完整时, 应 从其他图表中获取这些未知内容的信息, 然后运用 频数、频率知识进行计算, 补全图表中缺少的内容, 进而根据补全的内容解决其他实际问题. 链接3 [娄底中考]根据频数分布表或频数直 方图求加权平均数时, 统计中常用各组的组中值代 表各组的实际数据, 把各组的频数看作相应组中值 的权, 请你依据以上知识, 解决下面的实际问题.
为了解5路公共汽车的运营情况, 公交部门统 计了某天5路公共汽车每个运行班次的载客量, 并 按载客量的多少分成A, B, C, D四组, 得到如下统 计图:(1)求A组对应扇形圆心角的度数,并写出这 天载客量的中位数所在的组;(2)求这天5路公共汽车平均每班次的载客量;(3)如果一个月按30天计算,请估计5路公共 汽车一个月的总载客量,并把结果用科学记数法 表示出来.分析 (1)利用360°乘A组所占的比例即可;
(2)首先计算出各组的组中值,然后再利用加权平 均数公式计算平均数;
(3)利用平均每班次的载客 量×天数×次数可得一个月的总载客量.解: (1)由运营情况频数直方图可知共运营 10+16+18+6=50(次).
A组对应扇形圆心角的度数 为360°× =72°.
这天载客量的中位数在B组.
(2)各组组中值分别如下:A, 10;B, 30;C, 50;D, 70.
答:这天5路公共汽车平均每班次的载客量是 38人. (3)38×50×30=57 000=5.7×104 (人).
答:估计5路公共汽车一个月的总载客量为 5.7×104 人.链接4 [酒泉中考] 中华文明, 源远流长, 中华 汉字, 寓意深广. 为传承中华优秀文化, 某校团委组 织了一次全校3000名学生参加的“汉字听写”大 赛. 为了解本次大赛的成绩, 校团委随机抽取了其中 200名学生的成绩(成绩x取整数, 总分100分)作为样 本进行统计, 制成如下不完整的统计图表:根据所给信息, 解答下列问题:
(1)m=_______,n=_______;
频数、频率分布表(2)补全频数直方图;
频数、频率分布表(3)这200名学生成绩的中位数会落在哪个分 数段?
频数、频率分布表(4)若成绩在90分以上(包括90分)为“优”等, 请你估计该校参加本次比赛的3000名学生中成绩 是“优”等的约有多少人?
频数、频率分布表解: (1)由题可知总数为200,
则10+30+40+ m+50=200, 解得m=70;
由频率总和为1, 得0.05+0.15+n+0.35+0.25= 1, 解得n=0.20.(2)补全的频数直方图如下所示:(3)200个数据的中位数为第100个和第101个 数据的平均数, 由频数、频率分布表, 可得第100个 和第101个数据均位于80≤x<90分数段,则这200 名学生成绩的中位数会落在80≤x<90分数段.
(4)由补全的频数直方图可知在随机抽取的 200个样本中,
成绩在90分以上(包括90分)的频率= =0.25, 3000×0.25=750(人).
答:估计该校参加本次比赛的3000名学生中 成绩是“优”等的人数约为750人.
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
