人教版高一物理必修一:4.6用牛顿运动定律解决问题(一)(共21张PPT)
文档属性
| 名称 | 人教版高一物理必修一:4.6用牛顿运动定律解决问题(一)(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 780.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-01-06 08:23:38 | ||
图片预览







文档简介
(共21张PPT)
第六节 牛顿运动定律的应用
例1:一个静止在水平面上的物体,质量是2kg,在6.4N的水平拉力作用下沿水平地面向右运动,地面与水平地面的滑动摩擦力是4.2N,求物体在4s末的速度和4s内发生的位移。
是不是我们熟悉的某种运动呢?
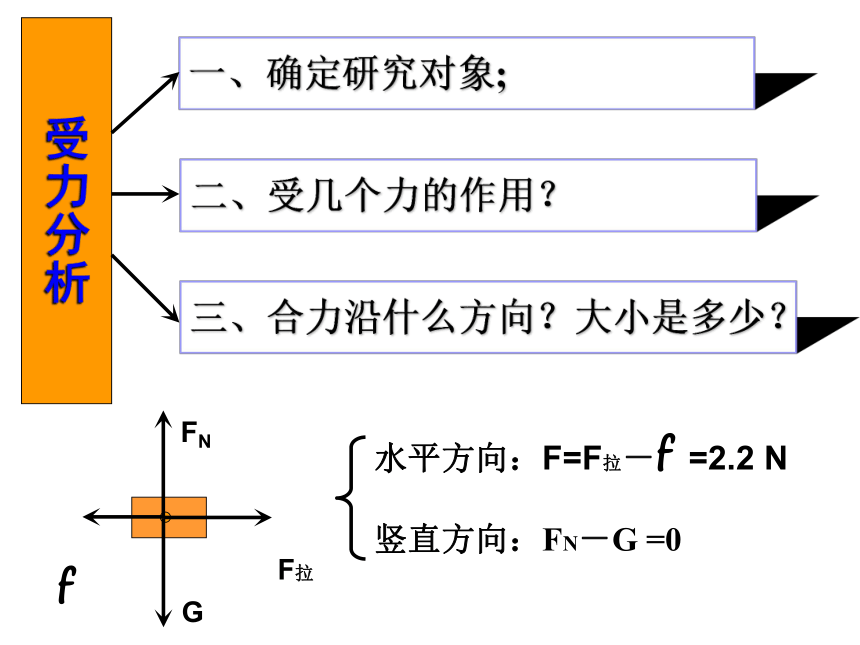
一、确定研究对象;
二、受几个力的作用?
三、合力沿什么方向?大小是多少?
受力分析
水平方向:F=F拉-f =2.2 N
竖直方向:FN-G =0
解:物体为研究对象,受力分析如图所示,取水平向右方向为正方向F=6.4N, f=4.2N,
所以F合= F- f= 2.2N
根据牛顿第二定律:F合=ma,得
a=F/m= 2.2÷2m/s2=1.1m/s2
所以物体在4s末的速度为4.4m/s,4s内发生的位移为8.8m
V
正
a
v =at=1.1 ×4 m/s=4.4 m/s
根据运动学公式得:
已知物体的受力情况,求物体运动情况的一般思路可以表述为:
研究对象
受力分析
合力F合
a
运动情况
二、已知物体运动情况求物体的受力情况
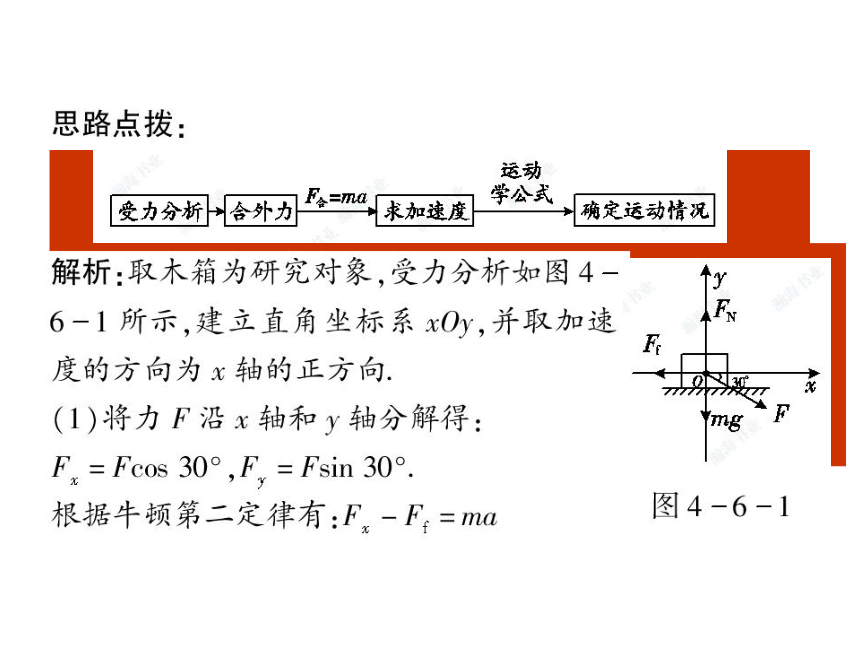
例2:一个滑雪的人,质量m=75kg,以v0=2m/s的初速度沿山坡匀加速滑下,山坡倾角θ=300,在t=5s的时间内滑下的路程s=60m,求滑雪人受到的阻力(包括滑动摩擦力和空气阻力)。
受力分析
合力沿什么方向?
合力沿斜面向下
受力方向复杂,如何求合力?
建立如图所示的直角坐标系——正交分解
Y
X
X:Gx - f =ma
Y:FN-GY =0
解:以人为研究对象,受力分析,建立如图坐标系,
F=Gx-f=m a ②
由运动学公式 x=v0 t+ at2 得
( f 方向沿斜面向上 )
1
2
Y
X
根据牛顿第二定律F=m a 得:
滑雪人受到的阻力f=-75 N
以加速度方向为正方向
v
a
正
已知物体的运动情况求物体的受力情况这一类问题的一般思路可表示为:
a
F合
受力分析
所求力
质量为0.5 kg的物体在与水平面成37°角的斜向上拉力F作用下,沿水平桌面静止向右做直线运动,经过0.5 m的距离,速度为2m/s,已知物体与桌面间的动摩擦因数μ=0.1,求作用力F的大小.
解:以物体为研究对象,受力分析,建立坐标系如图所示,
X
y
Fsin37?
Fcos37?
有(1)(2)(3)式可得:
正
v
a
取速度方向为正方向
1)已知物体的受力情况求物体的运动情况
2)已知物体的运动情况求物体的受力情况
可简单表示为:
1.为了安全,在公路上行驶的汽车之间保持必要的距离。已知某高速公路的最高限速v=108km/h,假设前方的车辆突然停止,后车司机从发现这一情况,经操纵刹车,到汽车开始减速所经历的时间(即反应时间)t=0.50s。刹车时汽车受到的阻力的大小f为汽车重力的0.40倍,该高速公路上汽车间的距离s至少应为多少?取重力加速度g=10m/s2。
解:以汽车为研究对象,减速运动受力分析如图,设反应时间内通过的位移为s1,匀减速过程通过的位移为s2
V0=108km/h=30m/s,t=0.5s,f=0. 4G,g=10m/s2
由s=vt得s1=30× 0.5m=15m
由牛顿第二定律:F合=ma,取初速度方向为正,得:
a= F合/m=- m/s2=-4m/S2
由Vt2- V02=2as,得:
S2= V02/2a=112.5m
S1+S2=127.5m
即高速公路上汽车间的距离至少应为127.5m
G
N
f
v
正
a
2.质量为100t的机车从停车场出发,经225m后,速度达到54km/h,此时,司机关闭发动机,让机车进站,机车又行驶125m才停在站上.设运动阻力不变,求机车关闭发动机前所受到的牵引力.
由牛顿第二定律得:
减速阶段
所以减速运动加速度的大小为
得阻力大小为
因而
第六节 牛顿运动定律的应用
例1:一个静止在水平面上的物体,质量是2kg,在6.4N的水平拉力作用下沿水平地面向右运动,地面与水平地面的滑动摩擦力是4.2N,求物体在4s末的速度和4s内发生的位移。
是不是我们熟悉的某种运动呢?
一、确定研究对象;
二、受几个力的作用?
三、合力沿什么方向?大小是多少?
受力分析
水平方向:F=F拉-f =2.2 N
竖直方向:FN-G =0
解:物体为研究对象,受力分析如图所示,取水平向右方向为正方向F=6.4N, f=4.2N,
所以F合= F- f= 2.2N
根据牛顿第二定律:F合=ma,得
a=F/m= 2.2÷2m/s2=1.1m/s2
所以物体在4s末的速度为4.4m/s,4s内发生的位移为8.8m
V
正
a
v =at=1.1 ×4 m/s=4.4 m/s
根据运动学公式得:
已知物体的受力情况,求物体运动情况的一般思路可以表述为:
研究对象
受力分析
合力F合
a
运动情况
二、已知物体运动情况求物体的受力情况
例2:一个滑雪的人,质量m=75kg,以v0=2m/s的初速度沿山坡匀加速滑下,山坡倾角θ=300,在t=5s的时间内滑下的路程s=60m,求滑雪人受到的阻力(包括滑动摩擦力和空气阻力)。
受力分析
合力沿什么方向?
合力沿斜面向下
受力方向复杂,如何求合力?
建立如图所示的直角坐标系——正交分解
Y
X
X:Gx - f =ma
Y:FN-GY =0
解:以人为研究对象,受力分析,建立如图坐标系,
F=Gx-f=m a ②
由运动学公式 x=v0 t+ at2 得
( f 方向沿斜面向上 )
1
2
Y
X
根据牛顿第二定律F=m a 得:
滑雪人受到的阻力f=-75 N
以加速度方向为正方向
v
a
正
已知物体的运动情况求物体的受力情况这一类问题的一般思路可表示为:
a
F合
受力分析
所求力
质量为0.5 kg的物体在与水平面成37°角的斜向上拉力F作用下,沿水平桌面静止向右做直线运动,经过0.5 m的距离,速度为2m/s,已知物体与桌面间的动摩擦因数μ=0.1,求作用力F的大小.
解:以物体为研究对象,受力分析,建立坐标系如图所示,
X
y
Fsin37?
Fcos37?
有(1)(2)(3)式可得:
正
v
a
取速度方向为正方向
1)已知物体的受力情况求物体的运动情况
2)已知物体的运动情况求物体的受力情况
可简单表示为:
1.为了安全,在公路上行驶的汽车之间保持必要的距离。已知某高速公路的最高限速v=108km/h,假设前方的车辆突然停止,后车司机从发现这一情况,经操纵刹车,到汽车开始减速所经历的时间(即反应时间)t=0.50s。刹车时汽车受到的阻力的大小f为汽车重力的0.40倍,该高速公路上汽车间的距离s至少应为多少?取重力加速度g=10m/s2。
解:以汽车为研究对象,减速运动受力分析如图,设反应时间内通过的位移为s1,匀减速过程通过的位移为s2
V0=108km/h=30m/s,t=0.5s,f=0. 4G,g=10m/s2
由s=vt得s1=30× 0.5m=15m
由牛顿第二定律:F合=ma,取初速度方向为正,得:
a= F合/m=- m/s2=-4m/S2
由Vt2- V02=2as,得:
S2= V02/2a=112.5m
S1+S2=127.5m
即高速公路上汽车间的距离至少应为127.5m
G
N
f
v
正
a
2.质量为100t的机车从停车场出发,经225m后,速度达到54km/h,此时,司机关闭发动机,让机车进站,机车又行驶125m才停在站上.设运动阻力不变,求机车关闭发动机前所受到的牵引力.
由牛顿第二定律得:
减速阶段
所以减速运动加速度的大小为
得阻力大小为
因而
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
