人教版数学九年级下册28.2 解直角三角形及其应用同步测试(优选2019年50道真题 含解析 )
文档属性
| 名称 | 人教版数学九年级下册28.2 解直角三角形及其应用同步测试(优选2019年50道真题 含解析 ) |
|
|
| 格式 | zip | ||
| 文件大小 | 956.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 00:00:00 | ||
图片预览


文档简介
28.2 解直角三角形及其应用
一.选择题(共20小题)
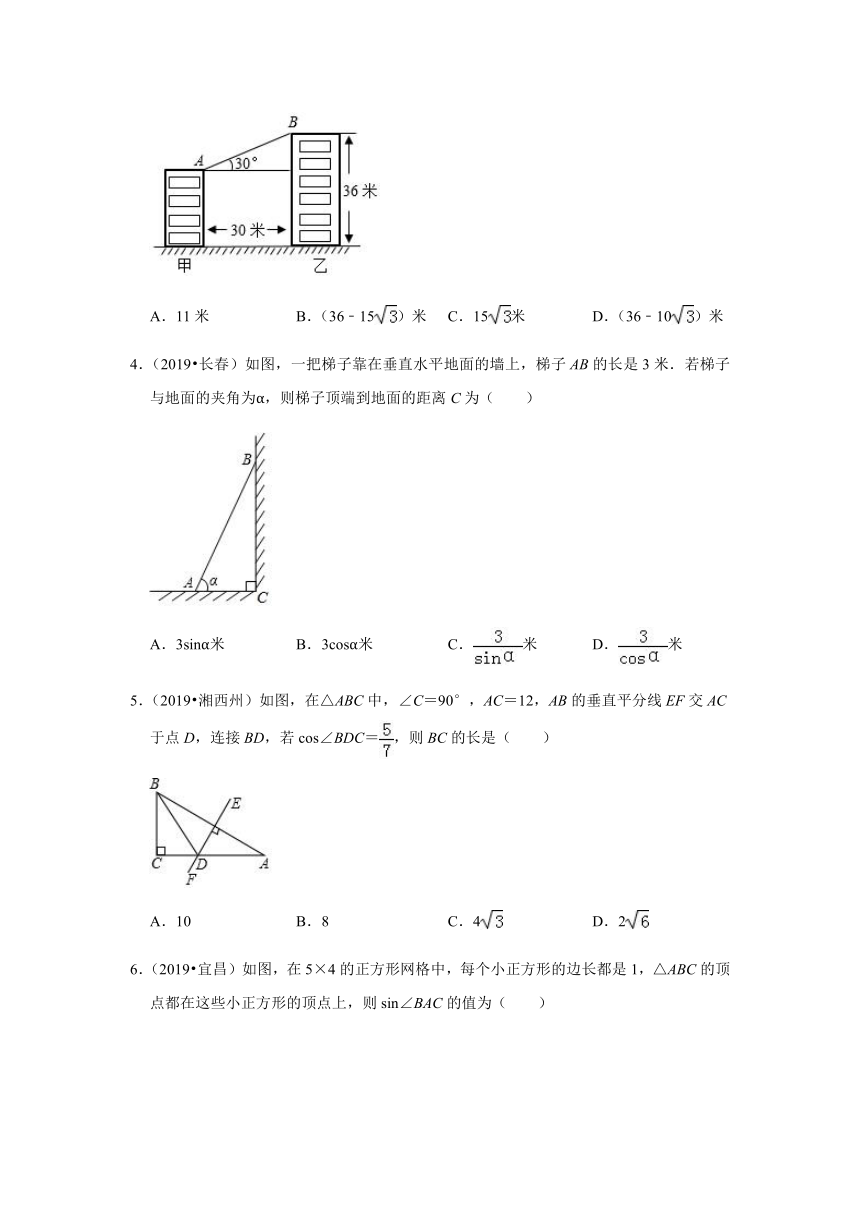
1.(2019?济南)某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为( )(参考数据:tan37°≈,tan53°≈)
A.225m B.275m C.300m D.315m
2.(2019?营口)如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是( )
A. B. C. D.
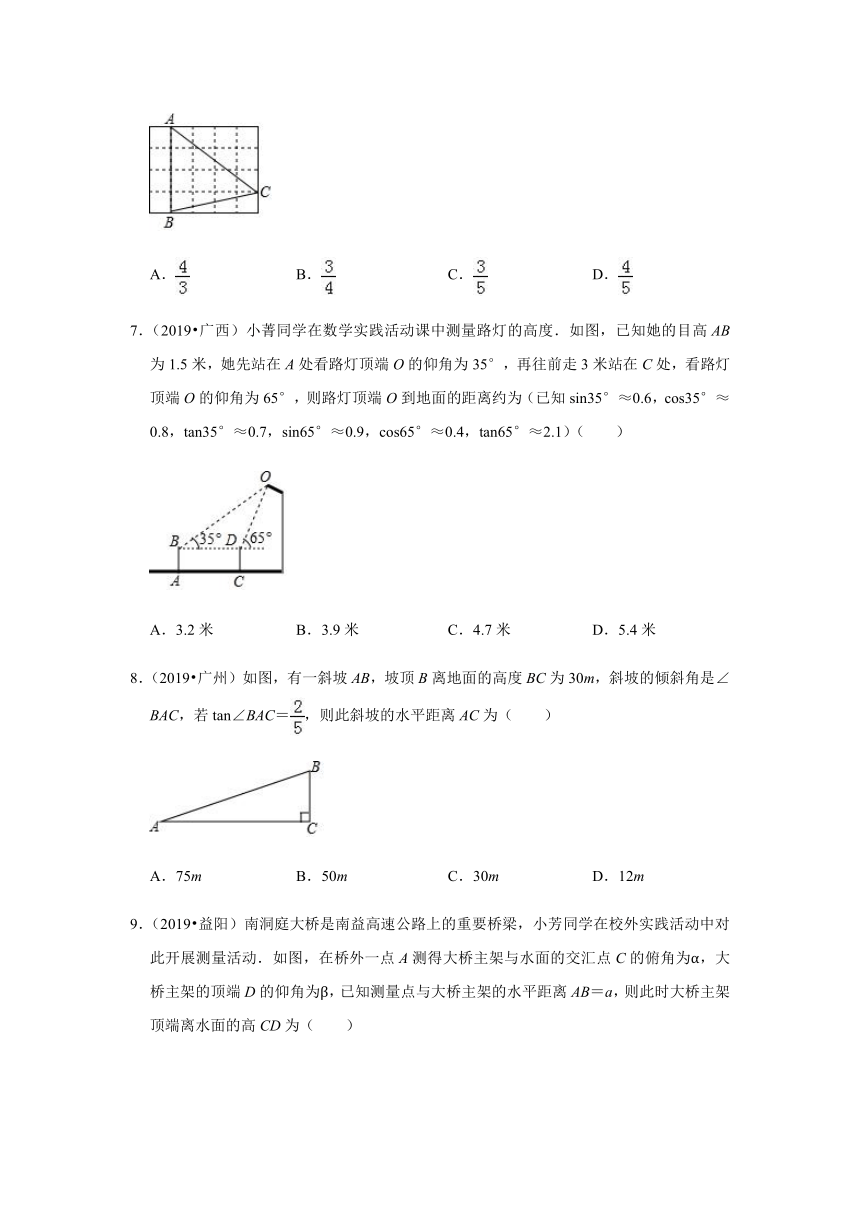
3.(2019?日照)如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A 处看乙楼楼顶B处仰角为30°,则甲楼高度为( )
A.11米 B.(36﹣15)米 C.15米 D.(36﹣10)米
4.(2019?长春)如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米.若梯子与地面的夹角为α,则梯子顶端到地面的距离C为( )
A.3sinα米 B.3cosα米 C.米 D.米
5.(2019?湘西州)如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是( )
A.10 B.8 C.4 D.2
6.(2019?宜昌)如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为( )
A. B. C. D.
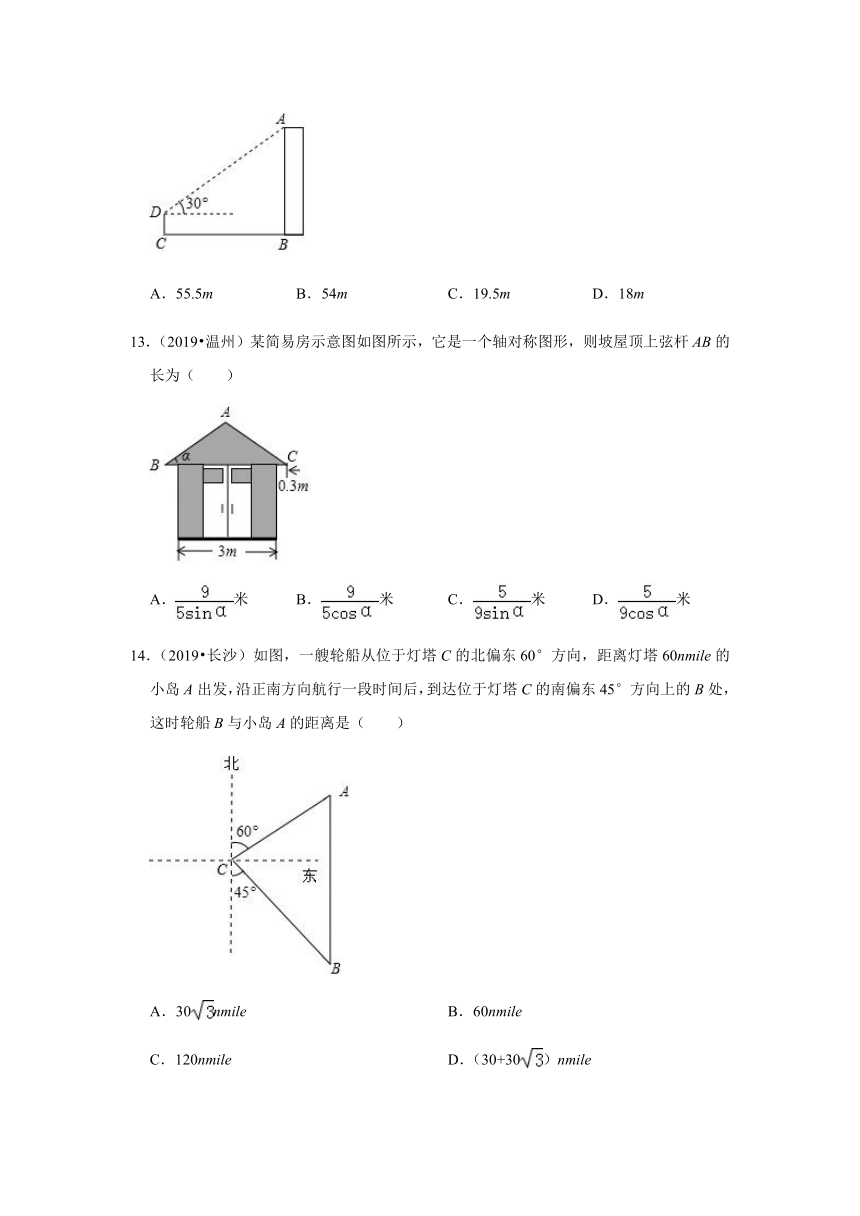
7.(2019?广西)小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高AB为1.5米,她先站在A处看路灯顶端O的仰角为35°,再往前走3米站在C处,看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为(已知sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)( )
A.3.2米 B.3.9米 C.4.7米 D.5.4米
8.(2019?广州)如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若tan∠BAC=,则此斜坡的水平距离AC为( )
A.75m B.50m C.30m D.12m
9.(2019?益阳)南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asinα+asinβ B.acosα+acosβ
C.atanα+atanβ D.+
10.(2019?河北)如图,从点C观测点D的仰角是( )
A.∠DAB B.∠DCE C.∠DCA D.∠ADC
11.(2019?长沙)如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是( )
A.2 B.4 C.5 D.10
12.(2019?苏州)如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18m的地面上,若测角仪的高度是1.5m.测得教学楼的顶部A处的仰角为30°.则教学楼的高度是( )
A.55.5m B.54m C.19.5m D.18m
13.(2019?温州)某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为( )
A.米 B.米 C.米 D.米
14.(2019?长沙)如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60nmile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )
A.30nmile B.60nmile
C.120nmile D.(30+30)nmile
15.(2019?杭州)如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )
A.asinx+bsinx B.acosx+bcosx
C.asinx+bcosx D.acosx+bsinx
16.(2019?凉山州)如图,在△ABC中,CA=CB=4,cosC=,则sinB的值为( )
A. B. C. D.
17.(2019?威海)如图,一个人从山脚下的A点出发,沿山坡小路AB走到山顶B点.已知坡角为20°,山高BC=2千米.用科学计算器计算小路AB的长度,下列按键顺序正确的是( )
A. B.
C. D.
18.(2019?重庆)如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1:2.4,那么建筑物AB的高度约为( )
(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
A.65.8米 B.71.8米 C.73.8米 D.119.8米
19.(2019?重庆)为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为( )
(参考数据:sin48°≈0.73,cos48°≈0.67,tan48°≈1.11)
A.17.0米 B.21.9米 C.23.3米 D.33.3米
20.(2019?泰安)如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为( )km.
A.30+30 B.30+10 C.10+30 D.30
二.填空题(共20小题)
21.(2019?阜新)如图,一艘船以40nmile/h的速度由西向东航行,航行到A处时,测得灯塔P在船的北偏东30°方向上,继续航行2.5h,到达B处,测得灯塔P在船的北偏西60°方向上,此时船到灯塔的距离为 nmile.(结果保留根号)
22.(2019?青海)如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则CD的长为 米.(结果保留根号)
23.(2019?葫芦岛)如图,河的两岸a,b互相平行,点A,B,C是河岸b上的三点,点P是河岸a上的一个建筑物,某人在河岸b上的A处测得∠PAB=30°,在B处测得∠PBC=75°,若AB=80米,则河两岸之间的距离约为 米.(≈1.73,结果精确到0.1米)
24.(2019?鄂尔多斯)如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若Rt△ABC是“好玩三角形”,且∠A=90°,则tan∠ABC= .
25.(2019?辽阳)某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车 (填“超速”或“没有超速”)(参考数据:≈1.732)
26.(2019?大连)如图,建筑物C上有一杆AB.从与BC相距10m的D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则旗杆AB的高度约为 m(结果取整数,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33).
27.(2019?徐州)如图,无人机于空中A处测得某建筑顶部B处的仰角为45°,测得该建筑底部C处的俯角为17°.若无人机的飞行高度AD为62m,则该建筑的高度BC为 m.
(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)
28.(2019?赤峰)如图,一根竖直的木杆在离地面3.1m处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为 m.
(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
29.(2019?柳州)如图,在△ABC中,sinB=,tanC=,AB=3,则AC的长为 .
30.(2019?舟山)如图,在△ABC中,若∠A=45°,AC2﹣BC2=AB2,则tanC= .
31.(2019?孝感)如图,在P处利用测角仪测得某建筑物AB的顶端B点的仰角为60°,点C的仰角为45°,点P到建筑物的距离为PD=20米,则BC= 米.
32.(2019?咸宁)如图所示,九(1)班数学课外活动小组在河边测量河宽AB(这段河流的两岸平行),他们在点C测得∠ACB=30°,点D处测得∠ADB=60°,CD=80m,则河宽AB约为 m(结果保留整数,≈1.73).
33.(2019?荆州)如图,灯塔A在测绘船的正北方向,灯塔B在测绘船的东北方向,测绘船向正东方向航行20海里后,恰好在灯塔B的正南方向,此时测得灯塔A在测绘船北偏西63.5°的方向上,则灯塔A,B间的距离为 海里(结果保留整数).(参考数据sin26.5°≈0.45,cos26.5°≈0.90,tan26.5°≈0.50,≈2.24)
34.(2019?天门)如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6m,则旗杆AB的高度为 m.
35.(2019?黄石)如图,一轮船在M处观测灯塔P位于南偏西30°方向,该轮船沿正南方向以15海里/小时的速度匀速航行2小时后到达N处,再观测灯塔P位于南偏西60°方向,若该轮船继续向南航行至灯塔P最近的位置T处,此时轮船与灯塔之间的距离PT为 海里(结果保留根号).
36.(2019?广东)如图,某校教学楼AC与实验楼BD的水平间距CD=15米,在实验楼顶部B点测得教学楼顶部A点的仰角是30°,底部C点的俯角是45°,则教学楼AC的高度是 米(结果保留根号).
37.(2019?宿迁)如图,∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=2,点C在射线AN上运动,当△ABC是锐角三角形时,BC的取值范围是 .
38.(2019?乐山)如图,在△ABC中,∠B=30°,AC=2,cosC=.则AB边的长为 .
39.(2019?温州)图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为 分米;当OB从水平状态旋转到OB'(在CO延长线上)时,点E绕点F随之旋转至OB'上的点E'处,则B'E'﹣BE为 分米.
40.(2019?衢州)如图,人字梯AB,AC的长都为2米,当α=50°时,人字梯顶端离地面的高度AD是 米(结果精确到0.1m.参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
三.解答题(共10小题)
41.(2019?恩施州)如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为30°,已知AB=6m,DE=10m.求乙楼的高度AC的长.(参考数据:≈1.41,≈1.73,精确到0.1m.)
42.(2019?盘锦)如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度.(精确到0.1m.参考数据:≈1.41,≈1.73)
43.(2019?营口)如图,A,B两市相距150km,国家级风景区中心C位于A市北偏东60°方向上,位于B市北偏西45°方向上.已知风景区是以点C为圆心、50km为半径的圆形区域.为了促进旅游经济发展,有关部门计划修建连接A,B两市的高速公路,高速公路AB是否穿过风景区?通过计算加以说明.(参考数据:≈1.73)
44.小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为60°,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为30°.已知山坡坡度i=3:4,即tanθ=,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据:≈1.732)
45.(2019?上海)图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD′E′的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.
(1)求点D′到BC的距离;
(2)求E、E′两点的距离.
46.(2019?遵义)某地为打造宜游环境,对旅游道路进行改造.如图是风景秀美的观景山,从山脚B到山腰D沿斜坡已建成步行道,为方便游客登顶观景,欲从D到A修建电动扶梯,经测量,山高AC=154米,步行道BD=168米,∠DBC=30°,在D处测得山顶A的仰角为45°.求电动扶梯DA的长(结果保留根号).
47.(2019?永州)为了测量某山(如图所示)的高度,甲在山顶A测得C处的俯角为45°,D处的俯角为30°,乙在山下测得C,D之间的距离为400米.已知B,C,D在同一水平面的同一直线上,求山高AB.(可能用到的数据:≈1.414,≈1.732)
48.(2019?湘潭)我国于2019年6月5日首次完成运载火箭海上发射,这标志着我国火箭发射技术达到了一个崭新的高度.如图,运载火箭从海面发射站点M处垂直海面发射,当火箭到达点A处时,海岸边N处的雷达站测得点N到点A的距离为8千米,仰角为30°.火箭继续直线上升到达点B处,此时海岸边N处的雷达测得B处的仰角增加15°,求此时火箭所在点B处与发射站点M处的距离.(结果精确到0.1千米)(参考数据:≈1.41,≈1.73)
49.(2019?陕西)小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米.已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB.(小平面镜的大小忽略不计)
50.(2019?内江)如图,两座建筑物DA与CB,其中CB的高为120米,从DA的顶点A测得CB顶部B的仰角为30°,测得其底部C的俯角为45°,求这两座建筑物的地面距离DC为多少米?(结果保留根号)
28.2 解直角三角形及其应用
参考答案与试题解析
一.选择题(共20小题)
1.(2019?济南)某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为( )(参考数据:tan37°≈,tan53°≈)
A.225m B.275m C.300m D.315m
解:如图,作CE⊥BA于E.设EC=xm,BE=ym.
在Rt△ECB中,tan53°=,即=,
在Rt△AEC中,tan37°=,即=,
解得x=180,y=135,
∴AC===300(m),
故选C.
2.(2019?营口)如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是( )
A. B. C. D.
解:∵AD∥BC,∠DAB=90°,
∴∠ABC=180°﹣∠DAB=90°,∠BAC+∠EAD=90°,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADB+∠EAD=90°,
∴∠BAC=∠ADB,
∴△ABC∽△DAB,
∴=,
∵BC=AD,
∴AD=2BC,
∴AB2=BC×AD=BC×2BC=2BC2,
∴AB=BC,
在Rt△ABC中,tan∠BAC===;
故选C.
3.(2019?日照)如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A 处看乙楼楼顶B处仰角为30°,则甲楼高度为( )
A.11米 B.(36﹣15)米 C.15米 D.(36﹣10)米
解:过点A作AE⊥BD,交BD于点E,
在Rt△ABE中,AE=30米,∠BAE=30°,
∴BE=30×tan30°=10(米),
∴AC=ED=BD﹣BE=(36﹣10)(米).
∴甲楼高为(36﹣10)米.
故选D.
4.(2019?长春)如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米.若梯子与地面的夹角为α,则梯子顶端到地面的距离C为( )
A.3sinα米 B.3cosα米 C.米 D.米
解:由题意可得sinα==,
故BC=3sinα(m).
故选A.
5.(2019?湘西州)如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是( )
A.10 B.8 C.4 D.2
解:∵∠C=90°,cos∠BDC=,
设CD=5x,BD=7x,
∴BC=2x,
∵AB的垂直平分线EF交AC于点D,
∴AD=BD=7x,
∴AC=12x,
∵AC=12,
∴x=1,
∴BC=2;
故选D.
6.(2019?宜昌)如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为( )
A. B. C. D.
解:如图,过C作CD⊥AB于D,则∠ADC=90°,
∴AC===5.
∴sin∠BAC==.
故选D.
7.(2019?广西)小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高AB为1.5米,她先站在A处看路灯顶端O的仰角为35°,再往前走3米站在C处,看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为(已知sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)( )
A.3.2米 B.3.9米 C.4.7米 D.5.4米
解:过点O作OE⊥AC于点F,延长BD交OE于点F,
设DF=x,
∵tan65°=,
∴OF=xtan65°,
∴BF=3+x,
∵tan35°=,
∴OF=(3+x)tan35°,
∴2.1x=0.7(3+x),
∴x=1.5,
∴OF=1.5×2.1=3.15,
∴OE=3.15+1.5=4.65,
故选C.
8.(2019?广州)如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若tan∠BAC=,则此斜坡的水平距离AC为( )
A.75m B.50m C.30m D.12m
解:∵∠BCA=90°,tan∠BAC=,BC=30m,
∴tan∠BAC=,
解得,AC=75,
故选A.
9.(2019?益阳)南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asinα+asinβ B.acosα+acosβ
C.atanα+atanβ D.+
解:在Rt△ABD和Rt△ABC中,AB=a,tanα=,tanβ=,
∴BC=atanα,BD=atanβ,
∴CD=BC+BD=atanα+atanβ;
故选C.
10.(2019?河北)如图,从点C观测点D的仰角是( )
A.∠DAB B.∠DCE C.∠DCA D.∠ADC
解:∵从点C观测点D的视线是CD,水平线是CE,
∴从点C观测点D的仰角是∠DCE,
故选B.
11.(2019?长沙)如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是( )
A.2 B.4 C.5 D.10
解:如图,作DH⊥AB于H,CM⊥AB于M.
∵BE⊥AC,
∴∠AEB=90°,
∵tanA==2,设AE=a,BE=2a,
则有:100=a2+4a2,
∴a2=20,
∴a=2或﹣2(舍弃),
∴BE=2a=4,
∵AB=AC,BE⊥AC,CM⊥AB,
∴CM=BE=4(等腰三角形两腰上的高相等))
∵∠DBH=∠ABE,∠BHD=∠BEA,
∴sin∠DBH===,
∴DH=BD,
∴CD+BD=CD+DH,
∴CD+DH≥CM,
∴CD+BD≥4,
∴CD+BD的最小值为4.
故选B.
12.(2019?苏州)如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18m的地面上,若测角仪的高度是1.5m.测得教学楼的顶部A处的仰角为30°.则教学楼的高度是( )
A.55.5m B.54m C.19.5m D.18m
解:过D作DE⊥AB,
∵在D处测得教学楼的顶部A的仰角为30°,
∴∠ADE=30°,
∵BC=DE=18m,
∴AE=DE?tan30°=18m,
∴AB=AE+BE=AE+CD=18+1.5=19.5m,
故选C.
13.(2019?温州)某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为( )
A.米 B.米 C.米 D.米
解:作AD⊥BC于点D,
则BD=0.3=,
∵cosα=,
∴cosα=,
解得,AB=米,
故选B.
14.(2019?长沙)如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60nmile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )
A.30nmile B.60nmile
C.120nmile D.(30+30)nmile
解:过C作CD⊥AB于D点,
∴∠ACD=30°,∠BCD=45°,AC=60.
在Rt△ACD中,cos∠ACD=,
∴CD=AC?cos∠ACD=60×=30.
在Rt△DCB中,∵∠BCD=∠B=45°,
∴CD=BD=30,
∴AB=AD+BD=30+30.
答:此时轮船所在的B处与灯塔P的距离是(30+30)nmile.
故选D.
15.(2019?杭州)如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )
A.asinx+bsinx B.acosx+bcosx
C.asinx+bcosx D.acosx+bsinx
解:作AE⊥OC于点E,作AF⊥OB于点F,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵∠ABC=∠AEC,∠BCO=x,
∴∠EAB=x,
∴∠FBA=x,
∵AB=a,AD=b,
∴FO=FB+BO=a?cosx+b?sinx,
故选D.
16.(2019?凉山州)如图,在△ABC中,CA=CB=4,cosC=,则sinB的值为( )
A. B. C. D.
解:过点A作AD⊥BC,垂足为D,如图所示.
在Rt△ACD中,CD=CA?cosC=1,
∴AD==;
在Rt△ABD中,BD=CB﹣CD=3,AD=,
∴AB==2,
∴sinB==.
故选D.
17.(2019?威海)如图,一个人从山脚下的A点出发,沿山坡小路AB走到山顶B点.已知坡角为20°,山高BC=2千米.用科学计算器计算小路AB的长度,下列按键顺序正确的是( )
A. B.
C. D.
解:在△ABC中,sinA=sin20°=,
∴AB==,
∴按键顺序为2÷sin20=
故选A.
18.(2019?重庆)如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1:2.4,那么建筑物AB的高度约为( )
(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
A.65.8米 B.71.8米 C.73.8米 D.119.8米
解:过点E作EM⊥AB与点M,延长ED交BC于G,
∵斜坡CD的坡度(或坡比)i=1:2.4,BC=CD=52米,
∴设DG=x,则CG=2.4x.
在Rt△CDG中,
∵DG2+CG2=DC2,即x2+(2.4x)2=522,解得x=20,
∴DG=20米,CG=48米,
∴EG=20+0.8=20.8米,BG=52+48=100米.
∵EM⊥AB,AB⊥BG,EG⊥BG,
∴四边形EGBM是矩形,
∴EM=BG=100米,BM=EG=20.8米.
在Rt△AEM中,
∵∠AEM=27°,
∴AM=EM?tan27°≈100×0.51=51米,
∴AB=AM+BM=51+20.8=71.8米.
故选B.
19.(2019?重庆)为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为( )
(参考数据:sin48°≈0.73,cos48°≈0.67,tan48°≈1.11)
A.17.0米 B.21.9米 C.23.3米 D.33.3米
解:如图,设CD与EA交于F,
∵=1:2.4=,
∴设CF=5k,AF=12k,
∴AC==13k=26,
∴k=2,
∴AF=24,CF=10,
∵AE=6,
∴EF=6+24=30,
∵∠DEF=48°,
∴tan48°===1.11,
∴DF=33.3,
∴CD=33.3﹣10=23.3,
答:古树CD的高度约为23.3米,
故选C.
20.(2019?泰安)如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为( )km.
A.30+30 B.30+10 C.10+30 D.30
解:根据题意得,∠CAB=65°﹣20°=45°,∠ACB=40°+20°=60°,AB=30,
过B作BE⊥AC于E,
∴∠AEB=∠CEB=90°,
在Rt△ABE中,∵∠ABE=45°,AB=30,
∴AE=BE=AB=30km,
在Rt△CBE中,∵∠ACB=60°,
∴CE=BE=10km,
∴AC=AE+CE=30+10,
∴A,C两港之间的距离为(30+10)km,
故选B.
二.填空题(共20小题)
21.(2019?阜新)如图,一艘船以40nmile/h的速度由西向东航行,航行到A处时,测得灯塔P在船的北偏东30°方向上,继续航行2.5h,到达B处,测得灯塔P在船的北偏西60°方向上,此时船到灯塔的距离为 50 nmile.(结果保留根号)
解:根据题意,得∠PAB=60°,∠PBA=30,AB=2.5×40=100(nmile),
∴∠P=180°﹣∠PAB﹣∠PBA=180°﹣60°﹣30°=90°.
在Rt△PAB中,PB=AB?sin∠PAB=100×=50(nmile).
故答案为50.
22.(2019?青海)如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则CD的长为 4﹣4 米.(结果保留根号)
解:在Rt△CMB中,∵∠CMB=90°,MB=AM+AB=12米,∠MBC=30°,
∴CM=MB?tan30°=12×=4,
在Rt△ADM中,∵∠AMD=90°,∠MAD=45°,
∴∠MAD=∠MDA=45°,
∴MD=AM=4米,
∴CD=CM﹣DM=(4﹣4)米,
故答案为4﹣4.
23.(2019?葫芦岛)如图,河的两岸a,b互相平行,点A,B,C是河岸b上的三点,点P是河岸a上的一个建筑物,某人在河岸b上的A处测得∠PAB=30°,在B处测得∠PBC=75°,若AB=80米,则河两岸之间的距离约为 54.6 米.(≈1.73,结果精确到0.1米)
解:过点A作AE⊥a于点E,过点B作BD⊥PA于点D,
∵∠PBC=75°,∠PAB=30°,
∴∠DPB=45°,
∵AB=80,
∴BD=40,AD=40,
∴PD=DB=40,
∴AP=AD+PD=40+40,
∵a∥b,
∴∠EPA=∠PAB=30°,
∴AE=AP=20+20≈54.6,
故答案为54.6
24.(2019?鄂尔多斯)如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若Rt△ABC是“好玩三角形”,且∠A=90°,则tan∠ABC= 或 .
解:①如图1中,
在Rt△ABC中,∠A=90°,CE是△ABC的中线,设AB=EC=2a,则AE=EB=a,AC=a,
∴tan∠ABC==.
②如图2中,
在Rt△ABC中,∠A=90°,BE是△ABC的中线,设EB=AC=2a,则AE=EC=a,AB=a,
∴tan∠ABC==.,
故答案为或.
25.(2019?辽阳)某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车 没有超速 (填“超速”或“没有超速”)(参考数据:≈1.732)
解:作AD⊥直线l于D,
在Rt△ADB中,∠ABD=45°,
∴BD=AD=100,
在Rt△ADB中,tan∠ACD=,
则CD==100≈173.2,
∴BC=173.2﹣100=73.2(米),
小汽车的速度为0.0732÷=52.704(千米/小时),
∵52.704千米/小时<速60千米/小时,
∴小汽车没有超速,
故答案为没有超速.
26.(2019?大连)如图,建筑物C上有一杆AB.从与BC相距10m的D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则旗杆AB的高度约为 3 m(结果取整数,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33).
解:在Rt△BCD中,tan∠BDC=,
则BC=CD?tan∠BDC=10,
在Rt△ACD中,tan∠ADC=,
则AC=CD?tan∠ADC≈10×1.33=13.3,
∴AB=AC﹣BC=3.3≈3(m),
故答案为3.
27.(2019?徐州)如图,无人机于空中A处测得某建筑顶部B处的仰角为45°,测得该建筑底部C处的俯角为17°.若无人机的飞行高度AD为62m,则该建筑的高度BC为 262 m.
(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)
解:作AE⊥BC于E,
则四边形ADCE为矩形,
∴EC=AD=62,
在Rt△AEC中,tan∠EAC=,
则AE=≈=200,
在Rt△AEB中,∠BAE=45°,
∴BE=AE=200,
∴BC=200+62=262(m),
则该建筑的高度BC为262m,
故答案为262.
28.(2019?赤峰)如图,一根竖直的木杆在离地面3.1m处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为 8.1 m.
(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
解:如图:AC=3.1m,∠B=38°,
∴AB==,
∴木杆折断之前高度=AC+AB=3.1+5=8.1(m)
故答案为8.1
29.(2019?柳州)如图,在△ABC中,sinB=,tanC=,AB=3,则AC的长为 .
解:过A作AD⊥BC,
在Rt△ABD中,sinB=,AB=3,
∴AD=AB?sinB=1,
在Rt△ACD中,tanC=,
∴=,即CD=,
根据勾股定理得AC===,
故答案为
30.(2019?舟山)如图,在△ABC中,若∠A=45°,AC2﹣BC2=AB2,则tanC= .
解:如图,过B作BD⊥AC于D,
∵∠A=45°,
∴∠ABD=∠A=45°,
∴AD=BD.
∵∠ADB=∠CDB=90°,
∴AB2=AD2+DB2=2BD2,BC2=DC2+BD2,
∴AC2﹣BC2=(AD+DC)2﹣(DC2+BD2)
=AD2+DC2+2AD?DC﹣DC2﹣BD2
=2AD?DC
=2BD?DC,
∵AC2﹣BC2=AB2,
∴2BD?DC=×2BD2,
∴DC=BD,
∴tanC===.
故答案为.
31.(2019?孝感)如图,在P处利用测角仪测得某建筑物AB的顶端B点的仰角为60°,点C的仰角为45°,点P到建筑物的距离为PD=20米,则BC= (20﹣20) 米.
解:在Rt△PBD中,tan∠BPD=,
则BD=PD?tan∠BPD=20,
在Rt△PBD中,∠CPD=45°,
∴CD=PD=20,
∴BC=BD﹣CD=20﹣20,
故答案为(20﹣20).
32.(2019?咸宁)如图所示,九(1)班数学课外活动小组在河边测量河宽AB(这段河流的两岸平行),他们在点C测得∠ACB=30°,点D处测得∠ADB=60°,CD=80m,则河宽AB约为 69 m(结果保留整数,≈1.73).
解:在Rt△ABC中,∠ACB=30°,∠ADB=60°,
∴∠DAC=30°,
∴DA=DC=80,
在Rt△ABD中,
,
∴==40≈69(米),
故答案为69.
33.(2019?荆州)如图,灯塔A在测绘船的正北方向,灯塔B在测绘船的东北方向,测绘船向正东方向航行20海里后,恰好在灯塔B的正南方向,此时测得灯塔A在测绘船北偏西63.5°的方向上,则灯塔A,B间的距离为 22 海里(结果保留整数).(参考数据sin26.5°≈0.45,cos26.5°≈0.90,tan26.5°≈0.50,≈2.24)
解:由题意得,MN=20,∠ANB=63.5°,∠BMN=45°,∠AMN=∠BNM=90°,
∴BN=MN=20,
如图,过A作AE⊥BN于E,
则四边形AMNE是矩形,
∴AE=MN=20,EN=AM,
∵AM=MN?tan26.5°=20×0.50=10,
∴BE=20﹣10=10,
∴AB==10≈22海里.
故答案为22.
34.(2019?天门)如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6m,则旗杆AB的高度为 14.4 m.
解:作DE⊥AB于E,如图所示:
则∠AED=90°,四边形BCDE是矩形,
∴BE=CD=9.6m,∠CDE=∠DEA=90°,
∴∠ADC=90°+30°=120°,
∵∠ACB=60°,
∴∠ACD=30°,
∴∠CAD=30°=∠ACD,
∴AD=CD=9.6m,
在Rt△ADE中,∠ADE=30°,
∴AE=AD=4.8m,
∴AB=AE+BE=4.8m+9.6m=14.4m;
故答案为14.4.
35.(2019?黄石)如图,一轮船在M处观测灯塔P位于南偏西30°方向,该轮船沿正南方向以15海里/小时的速度匀速航行2小时后到达N处,再观测灯塔P位于南偏西60°方向,若该轮船继续向南航行至灯塔P最近的位置T处,此时轮船与灯塔之间的距离PT为 15 海里(结果保留根号).
解:由题意得,MN=15×2=30海里,
∵∠PMN=30°,∠PNT=60°,
∴∠MPN=∠PMN=30°,
∴PN=MN=30海里,
∴PT=PN?sin∠PNT=15海里.
故答案为15.
36.(2019?广东)如图,某校教学楼AC与实验楼BD的水平间距CD=15米,在实验楼顶部B点测得教学楼顶部A点的仰角是30°,底部C点的俯角是45°,则教学楼AC的高度是 (15+15) 米(结果保留根号).
解:过点B作BE⊥AB于点E,
在Rt△BEC中,∠CBE=45°,BE=15;可得CE=BE×tan45°=15米.
在Rt△ABE中,∠ABE=30°,BE=15,可得AE=BE×tan30°=15米.
故教学楼AC的高度是AC=15米.
答:教学楼AC的高度是(15)米.
37.(2019?宿迁)如图,∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=2,点C在射线AN上运动,当△ABC是锐角三角形时,BC的取值范围是 <BC< .
解:如图,过点B作BC1⊥AN,垂足为C1,BC2⊥AM,交AN于点C2
在Rt△ABC1中,AB=2,∠A=60°
∴∠ABC1=30°
∴AC1=AB=1,由勾股定理得BC1=,
在Rt△ABC2中,AB=2,∠A=60°
∴∠AC2B=30°
∴AC2=4,由勾股定理得BC2=2,
当△ABC是锐角三角形时,点C在C1C2上移动,此时<BC<2.
故答案为<BC<2.
38.(2019?乐山)如图,在△ABC中,∠B=30°,AC=2,cosC=.则AB边的长为 .
解:如图,作AH⊥BC于H.
在Rt△ACH中,∵∠AHC=90°,AC=2,cosC=,
∴=,
∴CH=,
∴AH===,
在Rt△ABH中,∵∠AHB=90°,∠B=30°,
∴AB=2AH=,
故答案为.
39.(2019?温州)图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为 (5+5) 分米;当OB从水平状态旋转到OB'(在CO延长线上)时,点E绕点F随之旋转至OB'上的点E'处,则B'E'﹣BE为 4 分米.
解:如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J.
∵AM⊥CD,
∴∠QMP=∠MPO=∠OQM=90°,
∴四边形OQMP是矩形,
∴QM=OP,
∵OC=OD=10,∠COD=60°,
∴△COD是等边三角形,
∵OP⊥CD,
∴∠COP=∠COD=30°,
∴QM=OP=OC?cos30°=5(分米),
∵∠AOC=∠QOP=90°,
∴∠AOQ=∠COP=30°,
∴AQ=OA=5(分米),
∴AM=AQ+MQ=5+5.
∵OB∥CD,
∴∠BOD=∠ODC=60°
在Rt△OFK中,KO=OF?cos60°=2(分米),FK=OF?sin60°=2(分米),
在Rt△PKE中,EK==2(分米)
∴BE=10﹣2﹣2=(8﹣2)(分米),
在Rt△OFJ中,OJ=OF?cos60°=2(分米),FJ=2(分米),
在Rt△FJE′中,E′J==2,
∴B′E′=10﹣(2﹣2)=12﹣2,
∴B′E′﹣BE=4.
故答案为5+5,4.
40.(2019?衢州)如图,人字梯AB,AC的长都为2米,当α=50°时,人字梯顶端离地面的高度AD是 1.5 米(结果精确到0.1m.参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
解:∵sinα=,
∴AD=AC?sinα≈2×0.77=1.5,
故答案为1.5
三.解答题(共10小题)
41.(2019?恩施州)如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为30°,已知AB=6m,DE=10m.求乙楼的高度AC的长.(参考数据:≈1.41,≈1.73,精确到0.1m.)
解:如图,过点E作EF⊥AC于F,则四边形CDEF为矩形,
∴EF=CD,CF=DE=10,
设AC=xm,则CD=EF=xm,BF=(x﹣16)m,
在Rt△BEF中,∠EBF=60°,tan∠EBF=,
∴=,
∴x=24+8≈37.8m
答:乙楼的高度AC的长约为37.8m.
42.(2019?盘锦)如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度.(精确到0.1m.参考数据:≈1.41,≈1.73)
解:设CB部分的高度为xm.
∵∠BDC=∠BCD=45°,
∴BC=BD=xm.
在Rt△BCD中,CD===x(m).
在Rt△BCE中,∵∠BEC=30°,
∴CE=2BC=2x(m).
∵CE=CF=CD+DF,
∴2x=x+2,
解得x=2+.
∴BC=2+≈3.4(m).
答:CB部分的高度约为3.4m.
43.(2019?营口)如图,A,B两市相距150km,国家级风景区中心C位于A市北偏东60°方向上,位于B市北偏西45°方向上.已知风景区是以点C为圆心、50km为半径的圆形区域.为了促进旅游经济发展,有关部门计划修建连接A,B两市的高速公路,高速公路AB是否穿过风景区?通过计算加以说明.(参考数据:≈1.73)
解:高速公路AB不穿过风景区.
过点C作CH⊥AB于点H,如图所示.
根据题意,得∠CAB=30°,∠CBA=45°,
在Rt△CHB中,∵tan∠CBH==1,
∴CH=BH.
设BH=tkm,则CH=tkm,
在Rt△CAH中,∵tan∠CAH==,
∴AH=tkm.
∵AB=150km,
∴t+t=150,
∴t=75﹣75≈75×1.73﹣75=54.75.
∵54.75>50,
∴高速公路AB不穿过风景区.
44.小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为60°,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为30°.已知山坡坡度i=3:4,即tanθ=,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据:≈1.732)
解:作DC⊥EP交EP的延长线于C,作DF⊥ME于F,作PH⊥DF于H,
则DC=PH=FE,DH=CP,HF=PE,
设DC=3x,
∵tanθ=,
∴CP=4x,
由勾股定理得,PD2=DC2+CP2,即252=(3x)2+(4x)2,
解得,x=5,
则DC=3x=15,CP=4x=20,
∴DH=CP=20,PH=FE=DC=15,
设MF=ym,
则ME=(y+15)m,
在Rt△MDF中,tan∠MDF=,
则DF==y,
在Rt△MPE中,tan∠MPE=,
则PE==(y+15),
∵DH=DF﹣HF,
∴y﹣(y+15)=20,
解得,y=7.5+10,
∴ME=MF+FE=7.5+10+15≈39.8,
答:古塔的高度ME约为39.8m.
45.(2019?上海)图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD′E′的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.
(1)求点D′到BC的距离;
(2)求E、E′两点的距离.
解:(1)过点D′作D′H⊥BC,垂足为点H,交AD于点F,如图3所示.
由题意,得AD′=AD=90厘米,∠DAD′=60°.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFD′=∠BHD′=90°.
在Rt△AD′F中,D′F=AD′?sin∠DAD′=90×sin60°=45厘米.
又∵CE=40厘米,DE=30厘米,
∴FH=DC=DE+CE=70厘米,
∴D′H=D′F+FH=(45+70)厘米.
答:点D′到BC的距离为(45+70)厘米.
(2)连接AE,AE′,EE′,如图4所示.
由题意,得AE′=AE,∠EAE′=60°,
∴△AEE′是等边三角形,
∴EE′=AE.
∵四边形ABCD是矩形,
∴∠ADE=90°.
在Rt△ADE中,AD=90厘米,DE=30厘米,
∴AE==30厘米,
∴EE′=30厘米.
答:E、E′两点的距离是30厘米.
46.(2019?遵义)某地为打造宜游环境,对旅游道路进行改造.如图是风景秀美的观景山,从山脚B到山腰D沿斜坡已建成步行道,为方便游客登顶观景,欲从D到A修建电动扶梯,经测量,山高AC=154米,步行道BD=168米,∠DBC=30°,在D处测得山顶A的仰角为45°.求电动扶梯DA的长(结果保留根号).
解:作DE⊥BC于E,
则四边形DECF为矩形,
∴FC=DE,DF=EC,
在Rt△DBE中,∠DBC=30°,
∴DE=BD=84,
∴FC=DE=84,
∴AF=AC﹣FC=154﹣84=70,
在Rt△ADF中,∠ADF=45°,
∴AD=AF=70(米),
答:电动扶梯DA的长为70米.
47.(2019?永州)为了测量某山(如图所示)的高度,甲在山顶A测得C处的俯角为45°,D处的俯角为30°,乙在山下测得C,D之间的距离为400米.已知B,C,D在同一水平面的同一直线上,求山高AB.(可能用到的数据:≈1.414,≈1.732)
解:设AB=x,
由题意可知:∠ACB=45°,∠ADB=30°,
∴AB=BC=x,
∴BD=BC+CD=x+400,
在Rt△ADB中,
∴tan30°=,
∴=,
解得x=≈546.4,
∴山高AB为546.4米
48.(2019?湘潭)我国于2019年6月5日首次完成运载火箭海上发射,这标志着我国火箭发射技术达到了一个崭新的高度.如图,运载火箭从海面发射站点M处垂直海面发射,当火箭到达点A处时,海岸边N处的雷达站测得点N到点A的距离为8千米,仰角为30°.火箭继续直线上升到达点B处,此时海岸边N处的雷达测得B处的仰角增加15°,求此时火箭所在点B处与发射站点M处的距离.(结果精确到0.1千米)(参考数据:≈1.41,≈1.73)
解:如图所示:连接MN,由题意可得∠AMN=90°,∠ANM=30°,∠BNM=45°,AN=8km,
在直角△AMN中,MN=AN?cos30°=8×=4(km).
在直角△BMN中,BM=MN?tan45°=4km≈6.9km.
答:此时火箭所在点B处与发射站点M处的距离约为6.9km.
49.(2019?陕西)小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米.已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB.(小平面镜的大小忽略不计)
解:如图,过点C作CH⊥AB于点H,
则CH=BD,BH=CD=0.5.
在Rt△ACH中,∠ACH=45°,
∴AH=CH=BD,
∴AB=AH+BH=BD+0.5.
∵EF⊥FB,AB⊥FB,
∴∠EFG=∠ABG=90°.
由题意,易知∠EGF=∠AGB,
∴△EFG∽△ABG,
∴=即=,
解之,得BD=17.5,
∴AB=17.5+0.5=18(m).
∴这棵古树的高AB为18m.
50.(2019?内江)如图,两座建筑物DA与CB,其中CB的高为120米,从DA的顶点A测得CB顶部B的仰角为30°,测得其底部C的俯角为45°,求这两座建筑物的地面距离DC为多少米?(结果保留根号)
解:作AE⊥BC于E,
则四边形ADCE为矩形,
∴AD=CE,
设BE=x,
在Rt△ABE中,tanBAE=,
则AE==x,
∵∠EAC=45°,
∴EC=AE=x,
由题意得,BE+CE=120,即x+x=120,
解得,x=60(﹣1),
∴AD=CE=x=180﹣60,
∴DC=180﹣60,
答:两座建筑物的地面距离DC为(180﹣60)米.
