湘教版八年级数学下册第3章 图形与坐标章末复习课件(共35张)
文档属性
| 名称 | 湘教版八年级数学下册第3章 图形与坐标章末复习课件(共35张) |

|
|
| 格式 | zip | ||
| 文件大小 | 725.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-07 00:00:00 | ||
图片预览








文档简介
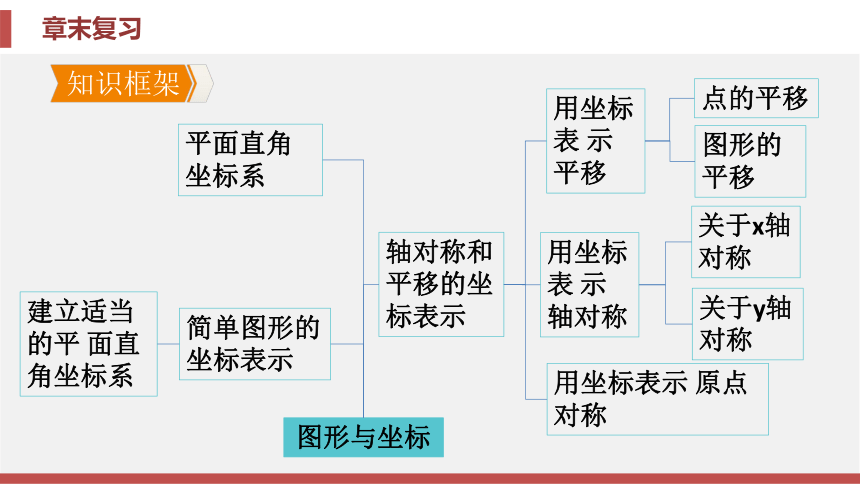
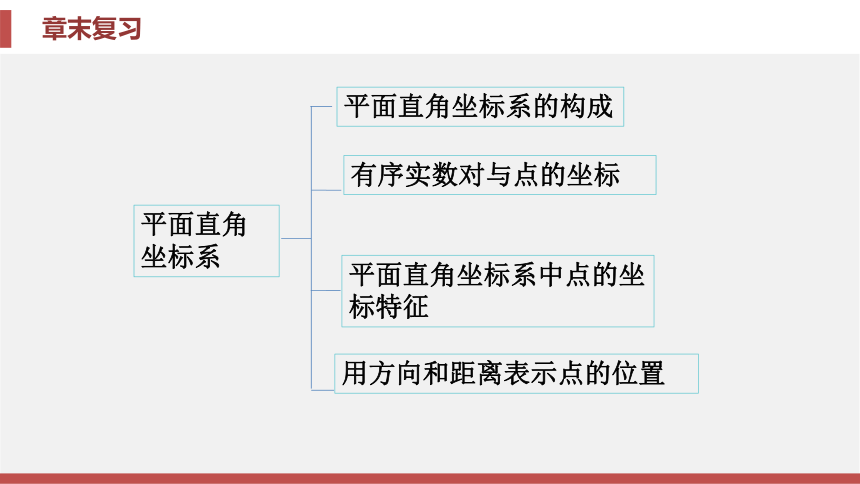
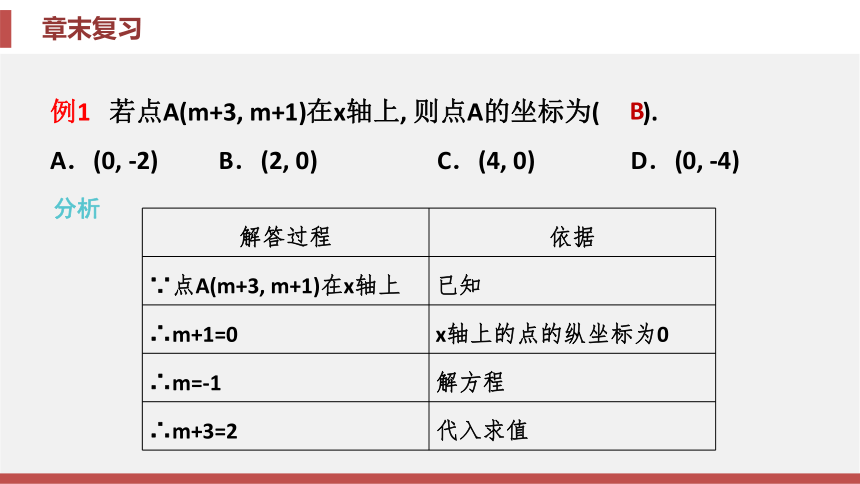
课件35张PPT。第3章 图形与坐标章末复习第3章 图形与坐标章末复习知识框架归纳整合素养提升中考链接知识框架【要点指导】平面直角坐标系由两条互相垂直的数轴组成, 这两条数轴 将坐标平面分成四个象限, 各象限内点的坐标特征如下:第一象限为(正, 正), 第二象限为(负, 正), 第三象限为(负, 负), 第四象限为(正, 负). x轴上的点的纵 坐标为0, y轴上的点的横坐标为0.归纳整合专题一 平面直角坐标系中点的坐标特征例1 若点A(m+3, m+1)在x轴上, 则点A的坐标为( ).
A.(0, -2) B.(2, 0) C.(4, 0) D.(0, -4)分析B相关题1 在平面直角坐标系中, 点 P(-2, x2 +1)所在的象限是( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限B[解析] ∵x2≥0,∴x2+1≥1,∴点P(-2,x2+1)在第二象限.故选B.【要点指导】在平面直角坐标系中, 图形的轴对称、平移变换不改变 图形的形状和大小, 图形的变换可以通过坐标变化体现出来, 常见的考查 方式是在平面直角坐标系中作图, 并写出相应点的坐标.专题二 轴对称、平移与坐标变化例2 已知点O(0, 0), D(4, 2), E(7, 7), C(2, 4).
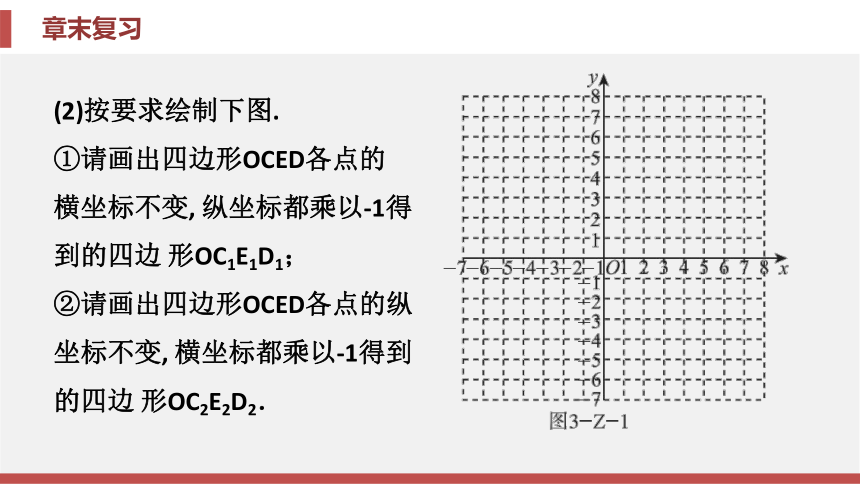
(1)在图3-Z-1的平面直角坐标系中, 描出各点并依次连接各点得到四 边形OCED. (2)按要求绘制下图.
①请画出四边形OCED各点的
横坐标不变, 纵坐标都乘以-1得
到的四边 形OC1E1D1;
②请画出四边形OCED各点的纵
坐标不变, 横坐标都乘以-1得到
的四边 形OC2E2D2.分析 (1)在平面直角坐标系中找出各点的位置, 然后顺次连接即可;
(2)①根据网格结构找出点C, E, D横坐标不变, 纵坐标都乘以-1的对应 点C1, E1, D1的位置, 再与点O顺次连接即可; ②根据网格结构找出点C, E, D纵坐标不变, 横坐标都乘以-1的对应点 C2, E2, D2的位置, 再与点O顺次连接即可.解: (1)四边形OCED如图3-Z-2所示.
(2)①四边形OC1E1D1如图3-Z-2所示; ②四边形OC2E2D2如图3-Z-2所示.相关题2 在如图3-Z-3所示的平 面直角坐标系中, 解答下 列问题: (1)在平面直角坐标系 中描出点A(2, 0), B(-1, -4), C(3, -3), 并连接得 到△ABC;
( 2 ) 将 △ ABC向上平 移4个单位
长度, 得到 △A1B1C1, 在图中画出
△A1B1C1; (3)求四边形A 1B1BA
的 周长.解:(1)△ABC如图所示.(2)△A1B1C1如图所示.【要点指导】有了坐标可以非常方便地描述点或图形经过轴对称(或平 移)变换后所得点或图形的位置, 解题时仍需注意“数”与“形”之间的联 系, 灵活运用数形结合的思想.素养提升专题一 数形结合思想例1 [重庆中考]如图3-Z-4, 已知△ABC三个顶点的 坐标分别为
A(-3, -2),B(0, -5), C(2, 4).
(1)若将△ABC向上平移5个单位
长度, 写出点A, B, C 的对应点A′,
B′, C′的坐标;
(2)试求△ABC的面积. 解: (1)A′(-3, 3), B′(0, 0), C′(2, 9).
(2)如图3-Z-4, 过点A作AE∥y轴, 过点B作BE∥x轴, 交AE于点E, 过点C 作CF∥y轴交EB的延长线于点F,
过点C作CD∥x轴, 交EA的延长线于点D.
∵DE∥y轴, CF∥y轴, CD∥x轴,
EF∥x轴, x轴⊥y轴,
∴DE⊥EF, CF⊥EF, DE⊥CD,
∴四边形DEFC为矩形. ∵S矩形DEFC=5×9=45, S△ADC= ×5×6=15, S△AEB= ×3×3=4.5, S△CBF= ×2×9=9,
∴S△ABC=S矩形DEFC-S△ADC-S△AEB-S△CBF
=45-15-4.5-9=16.5.相关题 1 如图3-Z-5, A, B, C为一 个平行四边形的三个顶 点, 且A, B, C三点的坐标 分别为(3, 3), (6, 4), (4, 6).
(1)请直接写出这个平行四 边形
第四个顶点的坐标;
(2)求这个平行四边形的 面积.【要点指导】解决有关分类讨论的问题, 关键是明确引起分类讨论的 条件, 并按照一定的原则或标准逐类进行讨论, 再把结论汇总得出问题的 答案. 分类的原则:(1)分类中的每一部分是相互独立的;(2)一次分类按一 个标准进行. 正确的分类必须是周全的, 既不重复也不遗漏.专题二 分类讨论思想例2 如图3-Z-6, 在平面直角坐标系中, O 为坐标原点, 四边形OABC为长方形, A(10, 0), C(0, 4), D为OA的中点, P为BC边上一点, 若△POD 为等腰三角形, 则满足条件的所有点P的坐标 为
__________________________ .(2.5, 4)或(3, 4)或(2, 4)或(8, 4)分析 △POD为等腰三角形, 但其顶角的顶点不确定, 因此需分情况讨 论. 分别以P, O, D为顶角的顶点进行讨论, 其中以D为顶点又有两种情况. 具 体分类讨论情况如下:①以P为顶角的顶点时, 点P在OD的垂直平分线上, 可 得点P的坐标为(2.5, 4);②以O为顶角的顶点时, 利用勾股定理, 可得点P的坐 标为(3, 4);③以D为顶角的顶点时, 可得点P的坐标为(2, 4)或(8, 4). 故满足条 件的所有点P的坐标为(2.5, 4)或(3, 4)或(2, 4)或(8, 4).相关题2-1 在平面直角坐标系中, 若点M(1, 3)与点N(x, 3) 之间的距离是5, 则x的 值为_________.-4或6相关题2-2 在平面直角坐标系 中, 已知点A(- , 0), B( , 0), 点C在坐标轴 上, 且 AC+BC= 6, 写出 满足条件的所有点C的 坐标
_________________________________.(3,0)或(-3,0)或(0,2)或(0,-2)中考链接母题1 (教材P90习题3.1 B组第7题)
你能判断A ( - 1 - a 2 , 3 + b 2 )是哪个象限的 点吗?考点:平面直角坐标系内点的坐标特征.
考情:本类知识常以选择题、填空题的形式考 查, 难度不大, 但易出错.
策略:画草图, 利用数形结合进行判断.链接1 [贵港中考]在平面直角坐标系中, 点 P(m-3, 4-2m)不可能在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限A分析 ①当m-3>0, 即m>3时, -2 m< -6 , 4-2m<-2, 所以, 点P(m-3, 4-2m)在第四象限, 不 可能在第一象限;
②当m-3<0,即m<3时, -2 m> -6 ,4-2m>-2, 所以点P(m-3, 4-2m)可以在第二或三象限. 综上 所述, 点P不可能在第一象限.母题2 (教材P106复习题3B组第8题)
如图3-Z-7, △ABC的坐标分别为A(6, 6), B(-3, 3), C(3, 3), 求△ABC的面积.考点:点的坐标的含义及点到坐标轴的距离.
考情:点到坐标轴的距离是中考的常考考点, 经 常出现在解答题中, 常用于求几何图形的面积, 必须牢固掌握.
策略:牢记点P(x, y)到x轴的距离为|y|, 到y轴的 距离为|x|.链接2 [扬州中考]在平面直角坐标系的第二 象限内有一点M, 点M到x轴的距离为3, 到y轴的距 离为4, 则点M的坐标是( ). A.(3, -4) B.(4, -3)
C.(-4, 3) D.(-3, 4)C分析 由题意, 得x=-4, y=3, 即M点的坐标是(-4, 3), 故选C.母题3 (教材P102习题3.3A组第1题)
填空:
(1)点A(5, -3)关于x轴对称的点的坐标是_________;
( 2 )点 B ( 3, 2 )关于y轴对称的点的坐标 是________;
(3)点P(-3, 5)向上平移2个单位长度, 它的像 是点P′________;
(4)点M(-3, 5)向左平移3个单位长度, 它的像 是点M′________.考点:图形平移、轴对称的坐标表示.
考情:本类知识在填空题、选择题、解答题中均 有涉及, 在解答题中常与三角形、四边形结合进 行证明或计算.
策略:抓住轴对称、平移的性质, 准确写出图形 变换前后对应点的坐标.链接3 [湘潭中考] 如图3-Z-8, 点A的坐标为 (-1, 2), 点A关于y轴的对称点的坐标为( ).
A.(1, 2) B.(-1, -2)
C.(1, -2) D.(2, -1)A分析 点A的坐标为(-1, 2), 点A关于y轴的对 称点的坐标为(1, 2).链接4 [长沙中考] 在平面直角坐标系中, 如 果将点A(-2, 3)向右平移3个单位长度, 再向下平 移2个单位长度, 那么平移后的对应点A′的坐标是 ______.(1, 1)分析 ∵将点A(-2, 3)向右平移3个单位长度, 再向下平移2个单位长度, 可以得到(-2+3, 3-2), ∴平移后的对应点A′的坐标是(1, 1).
谢 谢 观 看!
A.(0, -2) B.(2, 0) C.(4, 0) D.(0, -4)分析B相关题1 在平面直角坐标系中, 点 P(-2, x2 +1)所在的象限是( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限B[解析] ∵x2≥0,∴x2+1≥1,∴点P(-2,x2+1)在第二象限.故选B.【要点指导】在平面直角坐标系中, 图形的轴对称、平移变换不改变 图形的形状和大小, 图形的变换可以通过坐标变化体现出来, 常见的考查 方式是在平面直角坐标系中作图, 并写出相应点的坐标.专题二 轴对称、平移与坐标变化例2 已知点O(0, 0), D(4, 2), E(7, 7), C(2, 4).
(1)在图3-Z-1的平面直角坐标系中, 描出各点并依次连接各点得到四 边形OCED. (2)按要求绘制下图.
①请画出四边形OCED各点的
横坐标不变, 纵坐标都乘以-1得
到的四边 形OC1E1D1;
②请画出四边形OCED各点的纵
坐标不变, 横坐标都乘以-1得到
的四边 形OC2E2D2.分析 (1)在平面直角坐标系中找出各点的位置, 然后顺次连接即可;
(2)①根据网格结构找出点C, E, D横坐标不变, 纵坐标都乘以-1的对应 点C1, E1, D1的位置, 再与点O顺次连接即可; ②根据网格结构找出点C, E, D纵坐标不变, 横坐标都乘以-1的对应点 C2, E2, D2的位置, 再与点O顺次连接即可.解: (1)四边形OCED如图3-Z-2所示.
(2)①四边形OC1E1D1如图3-Z-2所示; ②四边形OC2E2D2如图3-Z-2所示.相关题2 在如图3-Z-3所示的平 面直角坐标系中, 解答下 列问题: (1)在平面直角坐标系 中描出点A(2, 0), B(-1, -4), C(3, -3), 并连接得 到△ABC;
( 2 ) 将 △ ABC向上平 移4个单位
长度, 得到 △A1B1C1, 在图中画出
△A1B1C1; (3)求四边形A 1B1BA
的 周长.解:(1)△ABC如图所示.(2)△A1B1C1如图所示.【要点指导】有了坐标可以非常方便地描述点或图形经过轴对称(或平 移)变换后所得点或图形的位置, 解题时仍需注意“数”与“形”之间的联 系, 灵活运用数形结合的思想.素养提升专题一 数形结合思想例1 [重庆中考]如图3-Z-4, 已知△ABC三个顶点的 坐标分别为
A(-3, -2),B(0, -5), C(2, 4).
(1)若将△ABC向上平移5个单位
长度, 写出点A, B, C 的对应点A′,
B′, C′的坐标;
(2)试求△ABC的面积. 解: (1)A′(-3, 3), B′(0, 0), C′(2, 9).
(2)如图3-Z-4, 过点A作AE∥y轴, 过点B作BE∥x轴, 交AE于点E, 过点C 作CF∥y轴交EB的延长线于点F,
过点C作CD∥x轴, 交EA的延长线于点D.
∵DE∥y轴, CF∥y轴, CD∥x轴,
EF∥x轴, x轴⊥y轴,
∴DE⊥EF, CF⊥EF, DE⊥CD,
∴四边形DEFC为矩形. ∵S矩形DEFC=5×9=45, S△ADC= ×5×6=15, S△AEB= ×3×3=4.5, S△CBF= ×2×9=9,
∴S△ABC=S矩形DEFC-S△ADC-S△AEB-S△CBF
=45-15-4.5-9=16.5.相关题 1 如图3-Z-5, A, B, C为一 个平行四边形的三个顶 点, 且A, B, C三点的坐标 分别为(3, 3), (6, 4), (4, 6).
(1)请直接写出这个平行四 边形
第四个顶点的坐标;
(2)求这个平行四边形的 面积.【要点指导】解决有关分类讨论的问题, 关键是明确引起分类讨论的 条件, 并按照一定的原则或标准逐类进行讨论, 再把结论汇总得出问题的 答案. 分类的原则:(1)分类中的每一部分是相互独立的;(2)一次分类按一 个标准进行. 正确的分类必须是周全的, 既不重复也不遗漏.专题二 分类讨论思想例2 如图3-Z-6, 在平面直角坐标系中, O 为坐标原点, 四边形OABC为长方形, A(10, 0), C(0, 4), D为OA的中点, P为BC边上一点, 若△POD 为等腰三角形, 则满足条件的所有点P的坐标 为
__________________________ .(2.5, 4)或(3, 4)或(2, 4)或(8, 4)分析 △POD为等腰三角形, 但其顶角的顶点不确定, 因此需分情况讨 论. 分别以P, O, D为顶角的顶点进行讨论, 其中以D为顶点又有两种情况. 具 体分类讨论情况如下:①以P为顶角的顶点时, 点P在OD的垂直平分线上, 可 得点P的坐标为(2.5, 4);②以O为顶角的顶点时, 利用勾股定理, 可得点P的坐 标为(3, 4);③以D为顶角的顶点时, 可得点P的坐标为(2, 4)或(8, 4). 故满足条 件的所有点P的坐标为(2.5, 4)或(3, 4)或(2, 4)或(8, 4).相关题2-1 在平面直角坐标系中, 若点M(1, 3)与点N(x, 3) 之间的距离是5, 则x的 值为_________.-4或6相关题2-2 在平面直角坐标系 中, 已知点A(- , 0), B( , 0), 点C在坐标轴 上, 且 AC+BC= 6, 写出 满足条件的所有点C的 坐标
_________________________________.(3,0)或(-3,0)或(0,2)或(0,-2)中考链接母题1 (教材P90习题3.1 B组第7题)
你能判断A ( - 1 - a 2 , 3 + b 2 )是哪个象限的 点吗?考点:平面直角坐标系内点的坐标特征.
考情:本类知识常以选择题、填空题的形式考 查, 难度不大, 但易出错.
策略:画草图, 利用数形结合进行判断.链接1 [贵港中考]在平面直角坐标系中, 点 P(m-3, 4-2m)不可能在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限A分析 ①当m-3>0, 即m>3时, -2 m< -6 , 4-2m<-2, 所以, 点P(m-3, 4-2m)在第四象限, 不 可能在第一象限;
②当m-3<0,即m<3时, -2 m> -6 ,4-2m>-2, 所以点P(m-3, 4-2m)可以在第二或三象限. 综上 所述, 点P不可能在第一象限.母题2 (教材P106复习题3B组第8题)
如图3-Z-7, △ABC的坐标分别为A(6, 6), B(-3, 3), C(3, 3), 求△ABC的面积.考点:点的坐标的含义及点到坐标轴的距离.
考情:点到坐标轴的距离是中考的常考考点, 经 常出现在解答题中, 常用于求几何图形的面积, 必须牢固掌握.
策略:牢记点P(x, y)到x轴的距离为|y|, 到y轴的 距离为|x|.链接2 [扬州中考]在平面直角坐标系的第二 象限内有一点M, 点M到x轴的距离为3, 到y轴的距 离为4, 则点M的坐标是( ). A.(3, -4) B.(4, -3)
C.(-4, 3) D.(-3, 4)C分析 由题意, 得x=-4, y=3, 即M点的坐标是(-4, 3), 故选C.母题3 (教材P102习题3.3A组第1题)
填空:
(1)点A(5, -3)关于x轴对称的点的坐标是_________;
( 2 )点 B ( 3, 2 )关于y轴对称的点的坐标 是________;
(3)点P(-3, 5)向上平移2个单位长度, 它的像 是点P′________;
(4)点M(-3, 5)向左平移3个单位长度, 它的像 是点M′________.考点:图形平移、轴对称的坐标表示.
考情:本类知识在填空题、选择题、解答题中均 有涉及, 在解答题中常与三角形、四边形结合进 行证明或计算.
策略:抓住轴对称、平移的性质, 准确写出图形 变换前后对应点的坐标.链接3 [湘潭中考] 如图3-Z-8, 点A的坐标为 (-1, 2), 点A关于y轴的对称点的坐标为( ).
A.(1, 2) B.(-1, -2)
C.(1, -2) D.(2, -1)A分析 点A的坐标为(-1, 2), 点A关于y轴的对 称点的坐标为(1, 2).链接4 [长沙中考] 在平面直角坐标系中, 如 果将点A(-2, 3)向右平移3个单位长度, 再向下平 移2个单位长度, 那么平移后的对应点A′的坐标是 ______.(1, 1)分析 ∵将点A(-2, 3)向右平移3个单位长度, 再向下平移2个单位长度, 可以得到(-2+3, 3-2), ∴平移后的对应点A′的坐标是(1, 1).
谢 谢 观 看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
