湘教版八年级下册数学 第2章 四边形复习课件(共76张PPT)
文档属性
| 名称 | 湘教版八年级下册数学 第2章 四边形复习课件(共76张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 00:00:00 | ||
图片预览









文档简介
(共76张PPT)
第2章
四边形
章末复习
第2章
四边形
章末复习
知识框架
归纳整合
素养提升
中考链接
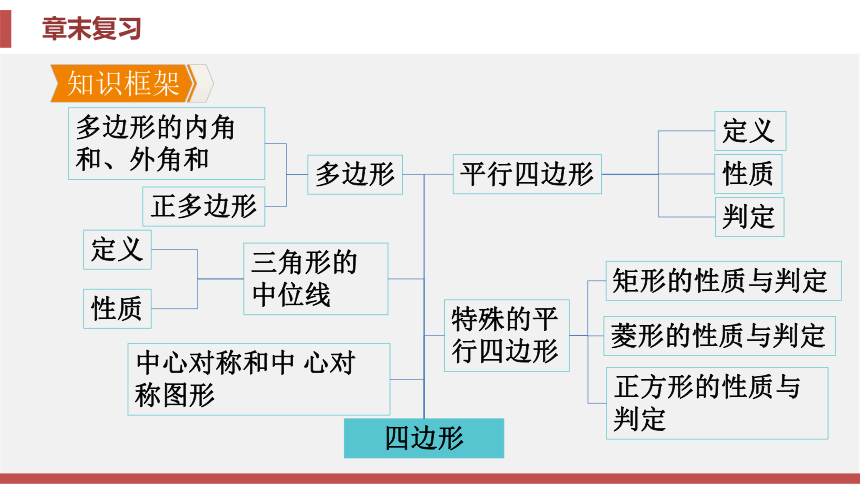
知识框架
多边形
定义
性质
三角形的
中位线
中心对称和中
心对称图形
四边形
定义
性质
平行四边形
矩形的性质与判定
菱形的性质与判定
特殊的平
行四边形
正方形的性质与判定
判定
多边形的内角
和、外角和
正多边形
【要点指导】涉及多边形内角和的计算,
通常有以下几种题型:
(1)已知多边形的边数,
求其内角和;
(2)已知多边形的内角和,
求其边数;
(3)已知多边形中内角和与外角和的关系,
求多边形的边数;
归纳整合
专题一
多边形的内角和与外角和
(4)正多边形
的边数与内角、外角的互求.
无论哪种形式的问题,
抓住多边形内角和公
式和外角和定理就能解决.注意n边形的内角和公式为(n-2)·180°,
其值
是变化的,
随着边数n的增加而增加;多边形的外角和都等于360°,
是一
个定值,
不随边数的变化而变化,
两者之间的联系是内角与其相邻的外角
之和为180°.
例1
[临沂中考]
一个正多边形的内角和为540°,
则这个正多边形的每
个外角的度数等于( ).
A.108°
B.90°
C.72°
D.60°
分析
设这个正多边形的边数为n.
因为正多边形的内角和是540°,
即
(n-2)·180°=540°,
解得n=5,
所以这个正多边形的每个外角的度数都是
360°÷5=72°.
C
相关题1
若一个多边形的内角和
是900°,
则这个多边形
的边数是( ).
A.10
B.9
C.8
D.7
D
【要点指导】平行四边形的性质与判定都可以从边、角、对角线的角
度去考虑,
平行四边形的性质有四种,
判定方法有五种,
应用时要认真领会它
们之间的联系与区别,
同时要根据条件合理、灵活地选择性质与判定方法.
专题二
平行四边形的性质和判定
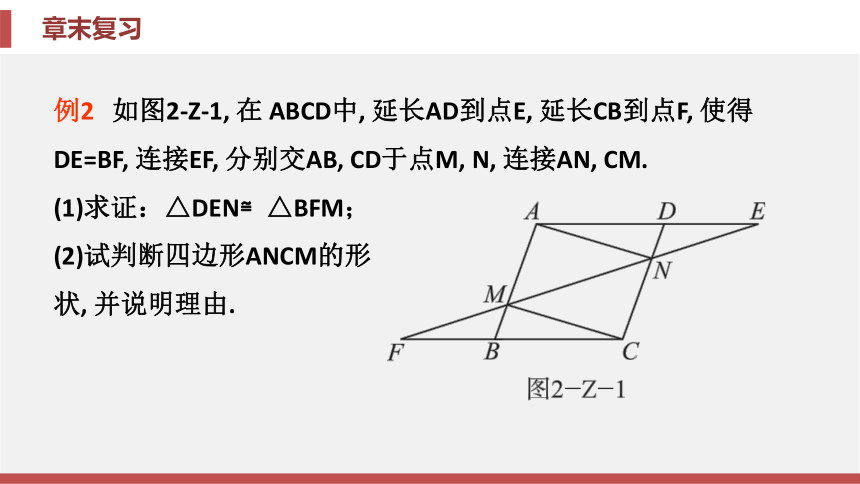
例2
如图2-Z-1,
在
ABCD中,
延长AD到点E,
延长CB到点F,
使得
DE=BF,
连接EF,
分别交AB,
CD于点M,
N,
连接AN,
CM.
(1)求证:△DEN≌△BFM;
(2)试判断四边形ANCM的形
状,
并说明理由.
解:
(1)证明:∵四边形ABCD是平行四边形,
∴AE∥CF,
∠ADC=∠ABC,
∴∠E=∠F,
∠EDN=∠FBM.
在△DEN和△BFM中,
∵∠E=∠F,
DE=BF,
∠EDN=∠FBM,
∴△DEN≌△BFM(ASA).
(2)四边形ANCM是平行四边形.理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,
AB∥CD,
即AM∥CN.
又由(1)知△DEN≌△BFM,
∴DN=BM,
∴CN=AM,
∴四边形ANCM是平行四边形.
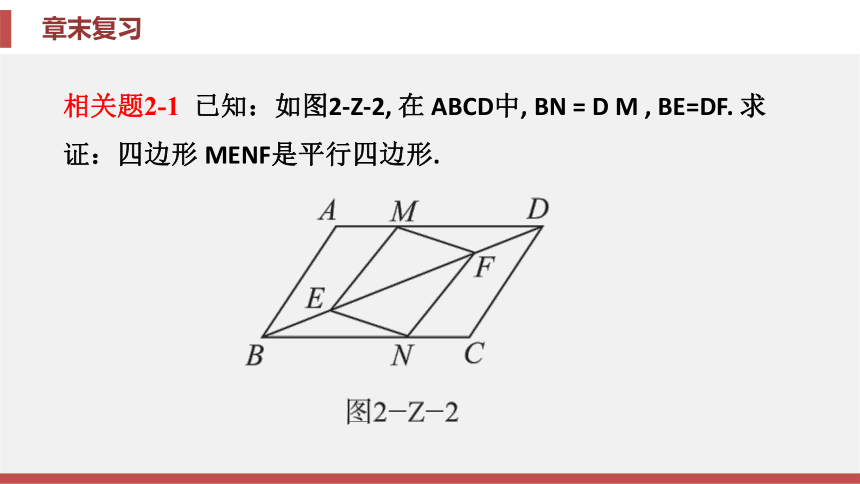
相关题2-1
已知:如图2-Z-2,
在
ABCD中,
BN
=
D
M
,
BE=DF.
求证:四边形
MENF是平行四边形.
证明:∵在 ABCD中,AD∥BC,∴∠CBD=∠ADB.
又∵BN=DM,BE=DF,∴△BNE≌△DMF,
则EN=FM,∠BEN=∠DFM,
∴∠FEN=∠EFM,∴EN∥FM,
∴四边形MENF是平行四边形.
相关题2-2
如图2-Z-3,
在
ABCD
中,
∠C=60°,
M,
N分
别是
A
D
,
B
C的中点
,
BC=2CD.
(1)求证:四边形MNCD
是平行四边形;
(2)求证:BD=
MN.
证明:
(1)∵四边形ABCD是平行四边形,
∴AD∥BC
,AD=BC.
∵M,N分别是AD,BC的中点,
∴MD=NC,MD∥NC,
∴四边形MNCD是平行四边形.
【要点指导】三角形中位线定理包含两个方面的内容:(1)三角形的
中位线平行于第三边;(2)三角形的中位线等于第三边的一半.
前者是两
条线段的位置关系;后者是线段与线段之间的数量关系.
定理的结论中既
包含线段的位置关系又包含线段的数量关系,
因此运用三角形中位线定理
既可以证明两直线平行,
又可以说明线段之间的数量关系.
专题三
三角形中位线定理
例3
已知:如图2-Z-4所示,
△ABC是锐角三角
形,
分别以AB,
AC为边向外侧作等边三角形ABM和等边
三角形CAN.
D,
E,
F分别是MB,
BC,
CN的中点,
连接DE,
EF.
求证:DE=EF.
证明:连接BN,
CM.
∵△ABM,
△CAN是等边三角形,
∴∠MAB=∠NAC=60°,
∴∠MAB+∠BAC=∠NAC+∠BAC,
即∠MAC=∠BAN.
在△MAC和△BAN中,
∵AM=AB,
∠MAC=∠BAN,
AC=AN,
∴△MAC≌△BAN,
∴MC=BN.
∵D,
E,
F分别是MB,
BC,
CN的中点,
∴DE,
EF分别是△MBC,
△BNC的中位线,
∴DE=
MC,
EF=
BN,
∴DE=EF.
相关题3
O是△ABC所在平面内
的一个动点,
连接OB,
OC,
并将AB,
OB,
OC,
AC的中点D,
E,
F,
G依次
连接起来,
设点D,
E,
F,
G能构成四边形.
(1)如图2-Z-5①,
当点
O在△ABC内部时,
求
证:四边形DEFG是平
行四边形;
图2-Z-5
(2)当点O在△ABC外时,
(1)中的结论是否仍然成
立(在图②中画出图形,
指出结论,
并说明理由)?
图2-Z-5
【要点指导】熟练掌握各类特殊平行四边形的定义、性质、判定方
法以及它们之间的联系和区别,
同时要灵活运用全等三角形、等腰三角
形、直角三角形等知识进行分析.
专题四
特殊平行四边形的性质和判定的应用
例4
[娄底中考]如图2-Z-6所示,
在矩形ABCD中,
M,
N分别是AD,
BC
的中点,
P,
Q分别是BM,
DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特
殊四边形?请说明理由.
解:(1)证明:在矩形ABCD中,
AB=CD,
AD=BC,
∠A=∠C=90°.
∵M,
N分别是AD,
BC的中点,
∴AM=CN.
AM=CN,
在△MBA和△NDC中,
∠A=∠C,
AB=CD,
∴△MBA≌△NDC(SAS).
(2)四边形MPNQ是菱形.
理由如下:如图2-Z-7所示,
连接MN.
∵M,
N分别是AD,
BC的中点,
∴MN∥AB∥CD,
∴∠BNM=∠DMN=90°.
∵P,
Q分别是BM,
DN的中点,
∴PN=MP=
BM,
MQ=QN=
DN.
由(1)知△MBA≌△NDC,
∴BM=DN,
∴PN=MP=MQ=QN,
∴四边形MPNQ是菱形.
相关题4
如图2-Z-8所示,
四边
形ABCD是边长为a的正
方形,
G,
E分别是边AB,
BC的中点,
∠AEF=90°,
且EF交正方形外角
∠
DCH的平分线CF于
点F.
(1)求证:∠BAE=∠FEC;
(2)求证:△AGE≌△ECF;
(3)求△AEF的面积.
解:(1)证明:因为∠AEF=90°,所以∠FEC+∠AEB=90°.
因为在正方形ABCD中,∠B=90°,
所以∠AEB+∠BAE=90°,所以∠BAE=∠FEC.
(2)证明:因为G,E分别是正方形ABCD的边AB,BC的中点,
所以AG=GB=BE=EC,且∠AGE=180°-45°=135°.
又因为CF是∠DCH的平分线,
所以∠ECF=180°-45°=135°,所以∠AGE=∠ECF.
因为在△AGE和△ECF中,∠GAE=∠CEF,AG=EC,
∠AGE=∠ECF,
所以△AGE≌△ECF.
【要点指导】化归思想就是将复杂的问题转化为简单的问题,
将陌生
的问题转化为熟悉的问题来处理的一种思想.
素养提升
专题一
化归思想在几何证明和计算中的应用
例1
如图2-Z-9,
四边形ABCD的对角线AC,
BD相交于点P,
过点P作直
线交AD于点E,
交BC于点F.
若PE=PF,
且AP+AE=CP+CF.
(1)求证:PA=PC;
(2)若AD=12,
AB=15,
∠DAB=60°,
求四边形ABCD的面积.
解:
(1)证明:如图2-Z-10,
在PA和PC的延长线上分别取点M,
N,
使AM=
AE,
CN=CF,
连接ME,MF,NE,NF.
∵AP+AE=CP+CF,
∴PM=PN.
又∵PE=PF,
∴四边形EMFN是平行四边形,
∴ME=FN,
∠EMA=∠CNF.
∵AM=AE,
CN=CF,
∴∠AME=∠AEM,
∠CNF=∠CFN,
∴△EAM≌△FCN,
∴AM=CN.
∵PM=PN,
∴PA=PC.
(2)连接EC,
AF,
∵PA=PC,
PE=PF,
∴四边形EAFC是平行四边形,
∴AE∥CF,
∴∠PED=∠PFB.
又∵∠EPD=∠FPB,
PE=PF,
∴△PED≌△PFB,
∴DP=BP.
由(1)知PA=PC,
∴四边形ABCD为平行四边形.
∵AD=12,
∠DAB=60°,
∴△ABD的AB边上的高为6
∴四边形ABCD的面积为90
.
相关题
1
如图2-Z-11所示,
在正
方形ABCD中,
点G,
F,
H,
E分别在边AB,
BC,
CD,
DA上,
且EF⊥GH.
求证:EF=GH.
证明:过点D作DK∥EF交BC于点K,
过点C作CL∥HG交AB于点L.
因为四边形ABCD是正方形,所以AB∥CD,AD∥BC,
所以四边形DEFK、四边形GLCH都是平行四边形,
所以EF=DK,GH=CL.由EF⊥GH知DK⊥CL.
由同角的余角相等知∠KDC=∠LCB.
又因为DC=CB,∠DCK=∠CBL,所以△DCK≌△CBL,
所以DK=CL,所以EF=GH.
【要点指导】在解决四边形的问题时,
有时无法直接求出有关线段的
长度或角的度数,
此时,
往往要通过设未知数,
列方程来解决.
专题二 方程思想在几何计算中的应用
例2
[大连中考]如图2-Z-12所示,
在矩形ABCD中,
AB=4,
BC=5,
E为BC上一点,
AF平分∠DAE,
EF⊥AE,
则CF
的长度为(
).
A.
B.1
C.
D.2
C
相关题2
把一张矩形纸片ABCD
按图2-Z-1
3所示的方
式折叠,
使点A与点E重
合,
点C与点F重合(E,
F
两点均在BD上),
折痕分
别为BH,
DG.
(1)求证:△BHE≌
△DGF;
(2)若AB=6,
BC=8,
求线
段FG的长.
中考链接
母题1
(教材P38练习第1题)
一个多边形的每一个外角都等于45°,
这个多
边形是几边形?它的每一个内角是多少度?
考点:n边形的内角和公式为(n-2)·180°,
外角
和为360°.
考情:此类题常以填空题、选择题的形式命题,
是中考中常考的知识点.
策略:可利用n边形的内角和为(n-2)·180°求
多边形的内角和或边数;可利用多边形的外角和
为360°求正多边形的外角或边数.
链接1
[邵阳中考]如图2-Z-14所示,
在四
边形ABCD中,
AD⊥AB,
∠C=110°,
它的一个外角
∠ADE=60°,
则∠B的度数是______.
40°
分析
∵∠ADE=60°,
∴∠ADC=120°.
∵AD⊥AB,
∴∠DAB=90°,
∴∠B=360°-∠C-∠ADC-∠A=40°.
故答案为40°.
链接2
[益阳中考]如图2-Z-15,
多边形ABCDE
的每个内角都相等,
则每个内角的度数为
______.
108°
母题2
(教材P50习题2.2B组第10题)
如图2-Z-16,
在
ABCD中,
AE⊥BD,
CF⊥BD,
垂
足分别为点E,
F.
求证:四边形AECF是平行四边形.
考点:平行四边形的性质定理、判定定理.
考情:平行四边形知识在整个初中几何中有着极
为重要的地位,
它上承全等三角形知识,
下连矩形、
菱形、正方形等特殊平行四边形知识,
是中考中的
必考知识点.
策略:熟记平行四边形的性质定理和判定定理,
结合全等三角形的知识,
依条件选用恰当的性质
定理和判定定理解题.
链接3
[衡阳中考]如图2-Z-17,
ABCD的
对角线相交于点O,
且AD≠CD,
过点O作OM⊥AC,
交AD于点M.如果
△
CDM的周长为8,
那么
ABCD的周长是______.
16
分析
∵四边形ABCD是平行四边形,
∴OA=OC.
∵OM⊥AC,
∴AM=MC,
∴△CDM的周长是AD+CD=8,
∴
ABCD的周长是2×8=16.
故答案为16.
链接4
[镇江中考]如图2-Z-18,
点B,
E分别
在AC,
DF上,
AF分别交BD,
CE于点M,
N,
∠A=∠F,
∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,
连接BN.
若BN平分∠DBC,
求
CN的长.
解:(1)证明:∵∠A=∠F,
∴DF∥AC.
又∵∠1=∠2,
∠1=∠3,
∴∠3=∠2,
∴DB∥EC,
∴四边形BCED为平行四边形.
(2)∵BN平分∠DBC,
∴∠DBN=∠NBC.
∵DB∥EC,
∴∠DBN
=∠BNC,
∴∠NBC
=∠BNC,
∴BC=CN.
∵四边形BCED为平行四边形,
∴BC=DE=2,
∴CN=2.
母题3
(教材P78复习题2A组第6题)
下列图形中不是中心对称图形的有(
).
考点:轴对称图形和中心对称图形的识别.
考情:此类题较简单,
中考中多以选择题的形式
出现.
策略:轴对称图形中一定能找到一条直线,
将图形
沿此直线对折,
左右两部分能完全重合.
识别中心对
称图形时,
只需将原图形倒转过来看,
若所得新图形
与原图形完全相同,
则此图形是中心对称图形.
链接5
[郴州中考]下列图形既是轴对称图形
又是中心对称图形的是
(
).
B
分析
轴对称图形与中心对称图形研究的都
是一个图形,
识别轴对称图形的关键是找对称轴,
若
能找到对称轴,
则此图形就是轴对称图形;识别中
心对称图形的关键是找对称中心,
若某图形绕某一
点旋转180°后能与自身重合,
则此图形就是中心对
称图形.
母题4
(教材P78复习题2A组第7题)
如图2-Z-21,
在四边形ABCD中,
P是对角
线AC的中点,
E,
F分别是AD,
BC的中点,
AB=DC,
∠PEF=18°,
求∠EPF的度数.
考点:三角形中位线的性质:①平行于第三边;
②长度等于第三边的一半.
考情:三角形中位线定理在证明两线平行、两角
相等,
求线段的长度,
证明线段的倍分关系中应用广
泛,
中考时填空题、选择题、解答题中均有涉及.
策略:当已知中出现三角形两边中点时,
应立即
联想三角形中位线的性质,
若图中无中位线,
则应
作辅助线构造中位线解题.
链接6
[徐州中考]在△ABC中,
D,
E分别是
AB,
AC的中点,
DE=7,
则BC=_______.
14
链接7
[绵阳中考]如图2-Z-22所示,
已知
AO是△ABC中∠BAC的平分线,
BD⊥AO的延长线
于点D,
E是BC的中点.
求证:DE=
(AB-AC).
证明:如图2-Z-22,
延长AC,
BD交于点F.
∵AD平分∠BAF,
AD⊥BD,
∴BD=DF,
AB=AF.
∵E是BC的中点,
∴BE=CE,
∴DE=
CF.
而CF=AF-AC,
∴DE=
(AB-AC).
母题5
(教材P64习题2.5B组第7题)
如图2-Z-23,
在矩形ABCD中,
对角线AC,
BD相
交于点O,
E,
F,
G,
H分别是OA,
OB,
OC,
OD的中点,
连
接EF,
FG,
GH,
HE.
求证:四边形EFGH是矩形.
考点:矩形、菱形、正方形的性质定理和判定定理.
考情:三类特殊平行四边形的边、角、对角线既
有共同特征,
也有各自特殊的性质.
判定方法均可从
边、角、对角线三个角度来寻找,
这是中考考查的
重点.
策略:熟记各类特殊平行四边形的性质定理与判
定定理,
弄清它们的区别和联系,
依条件灵活运用
性质定理和判定定理解题.
分析
∵四边形ABCD是矩形,
∴AC=BD=10,
BO=OD=
BD=5.
∵P,
Q分别是AO,
AD的中点,
∴PQ是△AOD的中位线,
∴PQ=
OD=2.5.
故答案为2.5.
链接8
[株洲中考]如图2-Z-24,
矩形ABCD
的对角线AC与BD相交点O,
AC=10,
P,
Q分别为AO,
AD的中点,
则PQ的长度为_____.
2.5
分析依照题意画出图形,
如图2-Z-25,
∵四边形ABCD是菱形,
∴AC⊥BD,
OA=OC,
OB=OD.
在Rt△AOB中,
AB=2,
OB=
,
∴OA=
=1,
∴AC=2OA=2,
∴S菱形ABCD=
AC·BD=
×2×2
=2
.
故答案为2
.
链接9
[黔南州中考]
已知一个菱形的边长
为2,
较长的对角线长为
,
则这个菱形的面积是_____.
分析
(1)延长AO到点E,
利用等边对等角和
角之间的关系解答即可;
(2)连接OC,
根据全等三角形的判定和性质以
及菱形的判定解答即可.
链接10
[南京中考]如图2-Z-26,
在四边形
ABCD中,
BC=CD,
∠BCD
=2∠BAD.O是四边形
ABCD内一点,
且OA=OB=OD.
求证:(1)∠BOD=∠BCD;
(2)四边形OBCD是菱形.
证明:
(1)如图2-Z-27,
延长AO到点E.
∵OA=OB,
∴∠ABO=∠BAO.
又∵∠BOE=∠ABO+∠BAO,
∴∠BOE=2∠BAO,
同理∠DOE=2∠DAO,
∴
∠
BOE
+
∠
DOE
=
2
∠
BAO
+
2
∠
DAO
=
2(∠BAO+∠DAO),
即∠BOD=2∠BAD.
又∵∠BCD=2∠BAD,
∴∠BOD=∠BCD.
(2)连接OC.
∵OB=OD,
BC=CD,
OC=OC,
∴△OBC≌△ODC,
∴∠BOC=∠DOC,
∠BCO=∠DCO.
∵∠BOD=∠BOC+∠DOC,
∠BCD=∠BCO+
∠DCO,
∴∠BOC=
∠BOD,
∠BCO=
∠BCD.
又∵∠BOD=∠BCD,
∴∠BOC=∠BCO,
∴OB=BC,
∴OB=BC=CD=OD,
∴四边形OBCD是菱形.
链接11
[盐城中考]在正方形ABCD中,
对角
线BD所在的直线上有两点E,
F满足BE=DF,
连接
AE,
AF,
CE,CF,
如图2-Z-28所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,
并说明理由.
分析
(1)根据正方形的性质和全等三角形的
判定证明即可;
(2)四边形AECF是菱形,
根据对角线互相垂直
的平行四边形是菱形即可判断.
解:(1)证明:∵四边形ABCD是正方形,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠ABE=∠ADF.
AB=AD,
在△ABE与△ADF中,
∠ABE=∠ADF,
BE=DF,
∴△ABE≌△ADF(SAS).
(2)四边形AECF是菱形.
理由:连接AC,
与BD交于点O,
如图2-Z-29.
∵四边形ABCD是正方形,
∴OA=OC,
OB=OD,
AC⊥EF,
∴OB+BE=OD+DF,
即OE=OF.
∵OA=OC,
OE=OF,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴
AECF是菱形.
谢
谢
观
看!
第2章
四边形
章末复习
第2章
四边形
章末复习
知识框架
归纳整合
素养提升
中考链接
知识框架
多边形
定义
性质
三角形的
中位线
中心对称和中
心对称图形
四边形
定义
性质
平行四边形
矩形的性质与判定
菱形的性质与判定
特殊的平
行四边形
正方形的性质与判定
判定
多边形的内角
和、外角和
正多边形
【要点指导】涉及多边形内角和的计算,
通常有以下几种题型:
(1)已知多边形的边数,
求其内角和;
(2)已知多边形的内角和,
求其边数;
(3)已知多边形中内角和与外角和的关系,
求多边形的边数;
归纳整合
专题一
多边形的内角和与外角和
(4)正多边形
的边数与内角、外角的互求.
无论哪种形式的问题,
抓住多边形内角和公
式和外角和定理就能解决.注意n边形的内角和公式为(n-2)·180°,
其值
是变化的,
随着边数n的增加而增加;多边形的外角和都等于360°,
是一
个定值,
不随边数的变化而变化,
两者之间的联系是内角与其相邻的外角
之和为180°.
例1
[临沂中考]
一个正多边形的内角和为540°,
则这个正多边形的每
个外角的度数等于( ).
A.108°
B.90°
C.72°
D.60°
分析
设这个正多边形的边数为n.
因为正多边形的内角和是540°,
即
(n-2)·180°=540°,
解得n=5,
所以这个正多边形的每个外角的度数都是
360°÷5=72°.
C
相关题1
若一个多边形的内角和
是900°,
则这个多边形
的边数是( ).
A.10
B.9
C.8
D.7
D
【要点指导】平行四边形的性质与判定都可以从边、角、对角线的角
度去考虑,
平行四边形的性质有四种,
判定方法有五种,
应用时要认真领会它
们之间的联系与区别,
同时要根据条件合理、灵活地选择性质与判定方法.
专题二
平行四边形的性质和判定
例2
如图2-Z-1,
在
ABCD中,
延长AD到点E,
延长CB到点F,
使得
DE=BF,
连接EF,
分别交AB,
CD于点M,
N,
连接AN,
CM.
(1)求证:△DEN≌△BFM;
(2)试判断四边形ANCM的形
状,
并说明理由.
解:
(1)证明:∵四边形ABCD是平行四边形,
∴AE∥CF,
∠ADC=∠ABC,
∴∠E=∠F,
∠EDN=∠FBM.
在△DEN和△BFM中,
∵∠E=∠F,
DE=BF,
∠EDN=∠FBM,
∴△DEN≌△BFM(ASA).
(2)四边形ANCM是平行四边形.理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,
AB∥CD,
即AM∥CN.
又由(1)知△DEN≌△BFM,
∴DN=BM,
∴CN=AM,
∴四边形ANCM是平行四边形.
相关题2-1
已知:如图2-Z-2,
在
ABCD中,
BN
=
D
M
,
BE=DF.
求证:四边形
MENF是平行四边形.
证明:∵在 ABCD中,AD∥BC,∴∠CBD=∠ADB.
又∵BN=DM,BE=DF,∴△BNE≌△DMF,
则EN=FM,∠BEN=∠DFM,
∴∠FEN=∠EFM,∴EN∥FM,
∴四边形MENF是平行四边形.
相关题2-2
如图2-Z-3,
在
ABCD
中,
∠C=60°,
M,
N分
别是
A
D
,
B
C的中点
,
BC=2CD.
(1)求证:四边形MNCD
是平行四边形;
(2)求证:BD=
MN.
证明:
(1)∵四边形ABCD是平行四边形,
∴AD∥BC
,AD=BC.
∵M,N分别是AD,BC的中点,
∴MD=NC,MD∥NC,
∴四边形MNCD是平行四边形.
【要点指导】三角形中位线定理包含两个方面的内容:(1)三角形的
中位线平行于第三边;(2)三角形的中位线等于第三边的一半.
前者是两
条线段的位置关系;后者是线段与线段之间的数量关系.
定理的结论中既
包含线段的位置关系又包含线段的数量关系,
因此运用三角形中位线定理
既可以证明两直线平行,
又可以说明线段之间的数量关系.
专题三
三角形中位线定理
例3
已知:如图2-Z-4所示,
△ABC是锐角三角
形,
分别以AB,
AC为边向外侧作等边三角形ABM和等边
三角形CAN.
D,
E,
F分别是MB,
BC,
CN的中点,
连接DE,
EF.
求证:DE=EF.
证明:连接BN,
CM.
∵△ABM,
△CAN是等边三角形,
∴∠MAB=∠NAC=60°,
∴∠MAB+∠BAC=∠NAC+∠BAC,
即∠MAC=∠BAN.
在△MAC和△BAN中,
∵AM=AB,
∠MAC=∠BAN,
AC=AN,
∴△MAC≌△BAN,
∴MC=BN.
∵D,
E,
F分别是MB,
BC,
CN的中点,
∴DE,
EF分别是△MBC,
△BNC的中位线,
∴DE=
MC,
EF=
BN,
∴DE=EF.
相关题3
O是△ABC所在平面内
的一个动点,
连接OB,
OC,
并将AB,
OB,
OC,
AC的中点D,
E,
F,
G依次
连接起来,
设点D,
E,
F,
G能构成四边形.
(1)如图2-Z-5①,
当点
O在△ABC内部时,
求
证:四边形DEFG是平
行四边形;
图2-Z-5
(2)当点O在△ABC外时,
(1)中的结论是否仍然成
立(在图②中画出图形,
指出结论,
并说明理由)?
图2-Z-5
【要点指导】熟练掌握各类特殊平行四边形的定义、性质、判定方
法以及它们之间的联系和区别,
同时要灵活运用全等三角形、等腰三角
形、直角三角形等知识进行分析.
专题四
特殊平行四边形的性质和判定的应用
例4
[娄底中考]如图2-Z-6所示,
在矩形ABCD中,
M,
N分别是AD,
BC
的中点,
P,
Q分别是BM,
DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特
殊四边形?请说明理由.
解:(1)证明:在矩形ABCD中,
AB=CD,
AD=BC,
∠A=∠C=90°.
∵M,
N分别是AD,
BC的中点,
∴AM=CN.
AM=CN,
在△MBA和△NDC中,
∠A=∠C,
AB=CD,
∴△MBA≌△NDC(SAS).
(2)四边形MPNQ是菱形.
理由如下:如图2-Z-7所示,
连接MN.
∵M,
N分别是AD,
BC的中点,
∴MN∥AB∥CD,
∴∠BNM=∠DMN=90°.
∵P,
Q分别是BM,
DN的中点,
∴PN=MP=
BM,
MQ=QN=
DN.
由(1)知△MBA≌△NDC,
∴BM=DN,
∴PN=MP=MQ=QN,
∴四边形MPNQ是菱形.
相关题4
如图2-Z-8所示,
四边
形ABCD是边长为a的正
方形,
G,
E分别是边AB,
BC的中点,
∠AEF=90°,
且EF交正方形外角
∠
DCH的平分线CF于
点F.
(1)求证:∠BAE=∠FEC;
(2)求证:△AGE≌△ECF;
(3)求△AEF的面积.
解:(1)证明:因为∠AEF=90°,所以∠FEC+∠AEB=90°.
因为在正方形ABCD中,∠B=90°,
所以∠AEB+∠BAE=90°,所以∠BAE=∠FEC.
(2)证明:因为G,E分别是正方形ABCD的边AB,BC的中点,
所以AG=GB=BE=EC,且∠AGE=180°-45°=135°.
又因为CF是∠DCH的平分线,
所以∠ECF=180°-45°=135°,所以∠AGE=∠ECF.
因为在△AGE和△ECF中,∠GAE=∠CEF,AG=EC,
∠AGE=∠ECF,
所以△AGE≌△ECF.
【要点指导】化归思想就是将复杂的问题转化为简单的问题,
将陌生
的问题转化为熟悉的问题来处理的一种思想.
素养提升
专题一
化归思想在几何证明和计算中的应用
例1
如图2-Z-9,
四边形ABCD的对角线AC,
BD相交于点P,
过点P作直
线交AD于点E,
交BC于点F.
若PE=PF,
且AP+AE=CP+CF.
(1)求证:PA=PC;
(2)若AD=12,
AB=15,
∠DAB=60°,
求四边形ABCD的面积.
解:
(1)证明:如图2-Z-10,
在PA和PC的延长线上分别取点M,
N,
使AM=
AE,
CN=CF,
连接ME,MF,NE,NF.
∵AP+AE=CP+CF,
∴PM=PN.
又∵PE=PF,
∴四边形EMFN是平行四边形,
∴ME=FN,
∠EMA=∠CNF.
∵AM=AE,
CN=CF,
∴∠AME=∠AEM,
∠CNF=∠CFN,
∴△EAM≌△FCN,
∴AM=CN.
∵PM=PN,
∴PA=PC.
(2)连接EC,
AF,
∵PA=PC,
PE=PF,
∴四边形EAFC是平行四边形,
∴AE∥CF,
∴∠PED=∠PFB.
又∵∠EPD=∠FPB,
PE=PF,
∴△PED≌△PFB,
∴DP=BP.
由(1)知PA=PC,
∴四边形ABCD为平行四边形.
∵AD=12,
∠DAB=60°,
∴△ABD的AB边上的高为6
∴四边形ABCD的面积为90
.
相关题
1
如图2-Z-11所示,
在正
方形ABCD中,
点G,
F,
H,
E分别在边AB,
BC,
CD,
DA上,
且EF⊥GH.
求证:EF=GH.
证明:过点D作DK∥EF交BC于点K,
过点C作CL∥HG交AB于点L.
因为四边形ABCD是正方形,所以AB∥CD,AD∥BC,
所以四边形DEFK、四边形GLCH都是平行四边形,
所以EF=DK,GH=CL.由EF⊥GH知DK⊥CL.
由同角的余角相等知∠KDC=∠LCB.
又因为DC=CB,∠DCK=∠CBL,所以△DCK≌△CBL,
所以DK=CL,所以EF=GH.
【要点指导】在解决四边形的问题时,
有时无法直接求出有关线段的
长度或角的度数,
此时,
往往要通过设未知数,
列方程来解决.
专题二 方程思想在几何计算中的应用
例2
[大连中考]如图2-Z-12所示,
在矩形ABCD中,
AB=4,
BC=5,
E为BC上一点,
AF平分∠DAE,
EF⊥AE,
则CF
的长度为(
).
A.
B.1
C.
D.2
C
相关题2
把一张矩形纸片ABCD
按图2-Z-1
3所示的方
式折叠,
使点A与点E重
合,
点C与点F重合(E,
F
两点均在BD上),
折痕分
别为BH,
DG.
(1)求证:△BHE≌
△DGF;
(2)若AB=6,
BC=8,
求线
段FG的长.
中考链接
母题1
(教材P38练习第1题)
一个多边形的每一个外角都等于45°,
这个多
边形是几边形?它的每一个内角是多少度?
考点:n边形的内角和公式为(n-2)·180°,
外角
和为360°.
考情:此类题常以填空题、选择题的形式命题,
是中考中常考的知识点.
策略:可利用n边形的内角和为(n-2)·180°求
多边形的内角和或边数;可利用多边形的外角和
为360°求正多边形的外角或边数.
链接1
[邵阳中考]如图2-Z-14所示,
在四
边形ABCD中,
AD⊥AB,
∠C=110°,
它的一个外角
∠ADE=60°,
则∠B的度数是______.
40°
分析
∵∠ADE=60°,
∴∠ADC=120°.
∵AD⊥AB,
∴∠DAB=90°,
∴∠B=360°-∠C-∠ADC-∠A=40°.
故答案为40°.
链接2
[益阳中考]如图2-Z-15,
多边形ABCDE
的每个内角都相等,
则每个内角的度数为
______.
108°
母题2
(教材P50习题2.2B组第10题)
如图2-Z-16,
在
ABCD中,
AE⊥BD,
CF⊥BD,
垂
足分别为点E,
F.
求证:四边形AECF是平行四边形.
考点:平行四边形的性质定理、判定定理.
考情:平行四边形知识在整个初中几何中有着极
为重要的地位,
它上承全等三角形知识,
下连矩形、
菱形、正方形等特殊平行四边形知识,
是中考中的
必考知识点.
策略:熟记平行四边形的性质定理和判定定理,
结合全等三角形的知识,
依条件选用恰当的性质
定理和判定定理解题.
链接3
[衡阳中考]如图2-Z-17,
ABCD的
对角线相交于点O,
且AD≠CD,
过点O作OM⊥AC,
交AD于点M.如果
△
CDM的周长为8,
那么
ABCD的周长是______.
16
分析
∵四边形ABCD是平行四边形,
∴OA=OC.
∵OM⊥AC,
∴AM=MC,
∴△CDM的周长是AD+CD=8,
∴
ABCD的周长是2×8=16.
故答案为16.
链接4
[镇江中考]如图2-Z-18,
点B,
E分别
在AC,
DF上,
AF分别交BD,
CE于点M,
N,
∠A=∠F,
∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,
连接BN.
若BN平分∠DBC,
求
CN的长.
解:(1)证明:∵∠A=∠F,
∴DF∥AC.
又∵∠1=∠2,
∠1=∠3,
∴∠3=∠2,
∴DB∥EC,
∴四边形BCED为平行四边形.
(2)∵BN平分∠DBC,
∴∠DBN=∠NBC.
∵DB∥EC,
∴∠DBN
=∠BNC,
∴∠NBC
=∠BNC,
∴BC=CN.
∵四边形BCED为平行四边形,
∴BC=DE=2,
∴CN=2.
母题3
(教材P78复习题2A组第6题)
下列图形中不是中心对称图形的有(
).
考点:轴对称图形和中心对称图形的识别.
考情:此类题较简单,
中考中多以选择题的形式
出现.
策略:轴对称图形中一定能找到一条直线,
将图形
沿此直线对折,
左右两部分能完全重合.
识别中心对
称图形时,
只需将原图形倒转过来看,
若所得新图形
与原图形完全相同,
则此图形是中心对称图形.
链接5
[郴州中考]下列图形既是轴对称图形
又是中心对称图形的是
(
).
B
分析
轴对称图形与中心对称图形研究的都
是一个图形,
识别轴对称图形的关键是找对称轴,
若
能找到对称轴,
则此图形就是轴对称图形;识别中
心对称图形的关键是找对称中心,
若某图形绕某一
点旋转180°后能与自身重合,
则此图形就是中心对
称图形.
母题4
(教材P78复习题2A组第7题)
如图2-Z-21,
在四边形ABCD中,
P是对角
线AC的中点,
E,
F分别是AD,
BC的中点,
AB=DC,
∠PEF=18°,
求∠EPF的度数.
考点:三角形中位线的性质:①平行于第三边;
②长度等于第三边的一半.
考情:三角形中位线定理在证明两线平行、两角
相等,
求线段的长度,
证明线段的倍分关系中应用广
泛,
中考时填空题、选择题、解答题中均有涉及.
策略:当已知中出现三角形两边中点时,
应立即
联想三角形中位线的性质,
若图中无中位线,
则应
作辅助线构造中位线解题.
链接6
[徐州中考]在△ABC中,
D,
E分别是
AB,
AC的中点,
DE=7,
则BC=_______.
14
链接7
[绵阳中考]如图2-Z-22所示,
已知
AO是△ABC中∠BAC的平分线,
BD⊥AO的延长线
于点D,
E是BC的中点.
求证:DE=
(AB-AC).
证明:如图2-Z-22,
延长AC,
BD交于点F.
∵AD平分∠BAF,
AD⊥BD,
∴BD=DF,
AB=AF.
∵E是BC的中点,
∴BE=CE,
∴DE=
CF.
而CF=AF-AC,
∴DE=
(AB-AC).
母题5
(教材P64习题2.5B组第7题)
如图2-Z-23,
在矩形ABCD中,
对角线AC,
BD相
交于点O,
E,
F,
G,
H分别是OA,
OB,
OC,
OD的中点,
连
接EF,
FG,
GH,
HE.
求证:四边形EFGH是矩形.
考点:矩形、菱形、正方形的性质定理和判定定理.
考情:三类特殊平行四边形的边、角、对角线既
有共同特征,
也有各自特殊的性质.
判定方法均可从
边、角、对角线三个角度来寻找,
这是中考考查的
重点.
策略:熟记各类特殊平行四边形的性质定理与判
定定理,
弄清它们的区别和联系,
依条件灵活运用
性质定理和判定定理解题.
分析
∵四边形ABCD是矩形,
∴AC=BD=10,
BO=OD=
BD=5.
∵P,
Q分别是AO,
AD的中点,
∴PQ是△AOD的中位线,
∴PQ=
OD=2.5.
故答案为2.5.
链接8
[株洲中考]如图2-Z-24,
矩形ABCD
的对角线AC与BD相交点O,
AC=10,
P,
Q分别为AO,
AD的中点,
则PQ的长度为_____.
2.5
分析依照题意画出图形,
如图2-Z-25,
∵四边形ABCD是菱形,
∴AC⊥BD,
OA=OC,
OB=OD.
在Rt△AOB中,
AB=2,
OB=
,
∴OA=
=1,
∴AC=2OA=2,
∴S菱形ABCD=
AC·BD=
×2×2
=2
.
故答案为2
.
链接9
[黔南州中考]
已知一个菱形的边长
为2,
较长的对角线长为
,
则这个菱形的面积是_____.
分析
(1)延长AO到点E,
利用等边对等角和
角之间的关系解答即可;
(2)连接OC,
根据全等三角形的判定和性质以
及菱形的判定解答即可.
链接10
[南京中考]如图2-Z-26,
在四边形
ABCD中,
BC=CD,
∠BCD
=2∠BAD.O是四边形
ABCD内一点,
且OA=OB=OD.
求证:(1)∠BOD=∠BCD;
(2)四边形OBCD是菱形.
证明:
(1)如图2-Z-27,
延长AO到点E.
∵OA=OB,
∴∠ABO=∠BAO.
又∵∠BOE=∠ABO+∠BAO,
∴∠BOE=2∠BAO,
同理∠DOE=2∠DAO,
∴
∠
BOE
+
∠
DOE
=
2
∠
BAO
+
2
∠
DAO
=
2(∠BAO+∠DAO),
即∠BOD=2∠BAD.
又∵∠BCD=2∠BAD,
∴∠BOD=∠BCD.
(2)连接OC.
∵OB=OD,
BC=CD,
OC=OC,
∴△OBC≌△ODC,
∴∠BOC=∠DOC,
∠BCO=∠DCO.
∵∠BOD=∠BOC+∠DOC,
∠BCD=∠BCO+
∠DCO,
∴∠BOC=
∠BOD,
∠BCO=
∠BCD.
又∵∠BOD=∠BCD,
∴∠BOC=∠BCO,
∴OB=BC,
∴OB=BC=CD=OD,
∴四边形OBCD是菱形.
链接11
[盐城中考]在正方形ABCD中,
对角
线BD所在的直线上有两点E,
F满足BE=DF,
连接
AE,
AF,
CE,CF,
如图2-Z-28所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,
并说明理由.
分析
(1)根据正方形的性质和全等三角形的
判定证明即可;
(2)四边形AECF是菱形,
根据对角线互相垂直
的平行四边形是菱形即可判断.
解:(1)证明:∵四边形ABCD是正方形,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠ABE=∠ADF.
AB=AD,
在△ABE与△ADF中,
∠ABE=∠ADF,
BE=DF,
∴△ABE≌△ADF(SAS).
(2)四边形AECF是菱形.
理由:连接AC,
与BD交于点O,
如图2-Z-29.
∵四边形ABCD是正方形,
∴OA=OC,
OB=OD,
AC⊥EF,
∴OB+BE=OD+DF,
即OE=OF.
∵OA=OC,
OE=OF,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴
AECF是菱形.
谢
谢
观
看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
