湘教版八年级数学下册 第1章 直角三角形复习课件(76张PPT)
文档属性
| 名称 | 湘教版八年级数学下册 第1章 直角三角形复习课件(76张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 00:00:00 | ||
图片预览







文档简介
(共76张PPT)
第1章
直角三角形
章末复习
第1章
直角三角形
章末复习
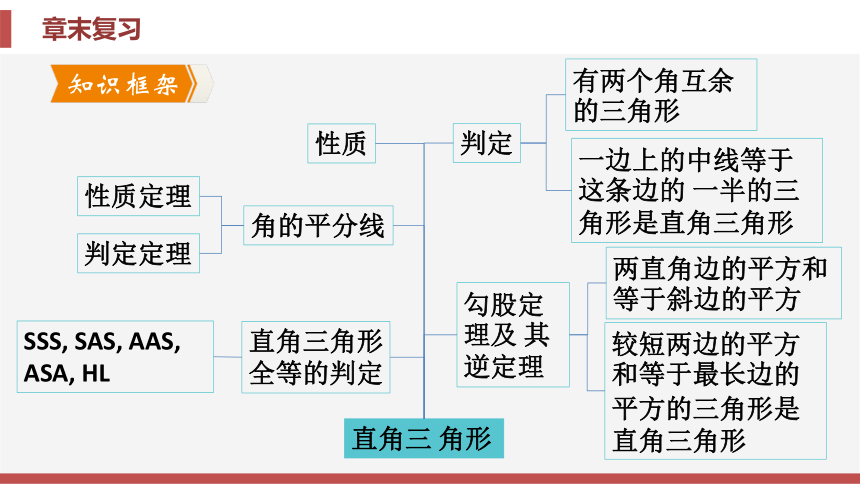
知识框架
归纳整合
素养提升
中考链接
知识框架
性质
性质定理
判定定理
角的平分线
SSS,
SAS,
AAS,
ASA,
HL
直角三角形
全等的判定
直角三
角形
有两个角互余的三角形
一边上的中线等于这条边的
一半的三角形是直角三角形
判定
两直角边的平方和等于斜边的平方
较短两边的平方和等于最长边的
平方的三角形是直角三角形
勾股定理及
其逆定理
两锐角互余
30°角所对的直角边等于
斜边的一半
性质
斜边上的中线等于斜边的一半
一直角边等于斜边的一半,
此直角边所对的角为30°
【要点指导】直角三角形的性质:①两锐角互余;②斜边上的中线等
于斜边的一半;③30°角所对的直角边等于斜边的一半;④若某直角边等于
斜边的一半,
则该直角边所对的锐角为30°.
解题时需灵活运用以上性质.
归纳整合
专题一
直角三角形的相关性质
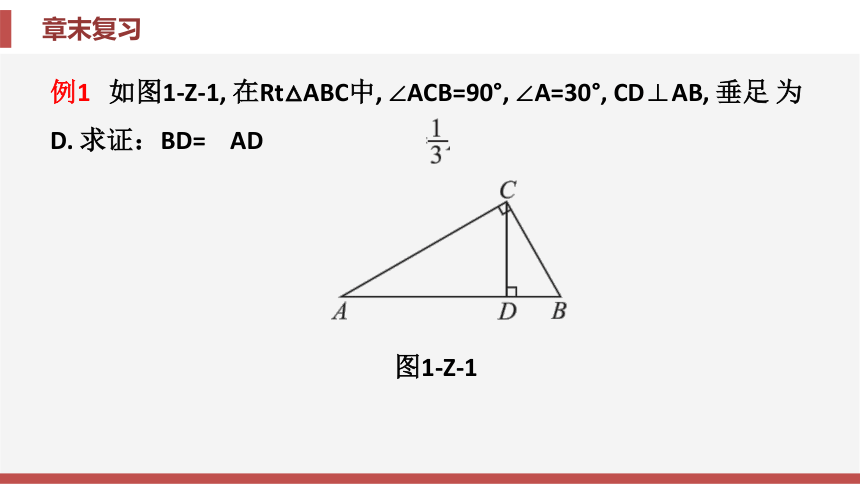
例1
如图1-Z-1,
在Rt△ABC中,
∠ACB=90°,
∠A=30°,
CD⊥AB,
垂足
为D.
求证:BD=
AD
图1-Z-1
证明:
∵CD⊥AB,
∠ACB=90°,
∴∠A+∠B=90°,
∠B+∠BCD=90°,
∴∠A=∠BCD.
∵∠A=30°,
∴∠BCD=30°,
∴BC=2BD.
∵∠A=30°,
∠ACB=90°,
∴AB=2BC,
∴AB=4BD.
∵AB=AD+BD,
∴AD=3BD,
∴BD=
AD.
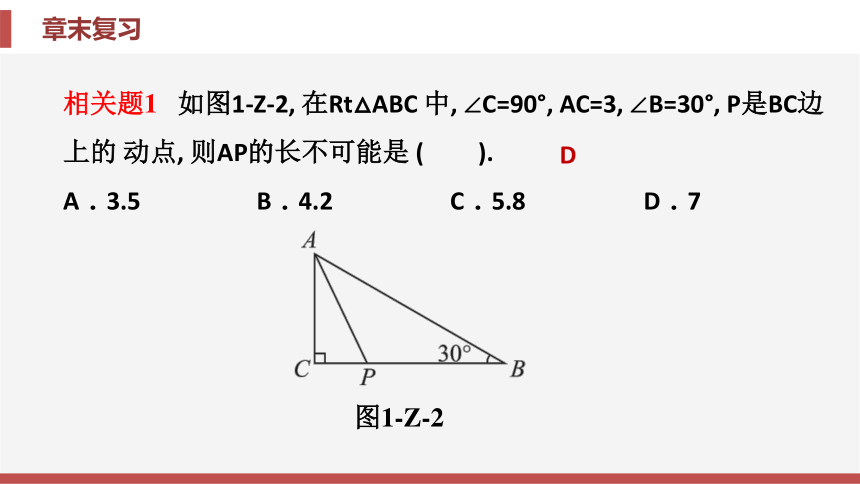
相关题1
如图1-Z-2,
在Rt△ABC
中,
∠C=90°,
AC=3,
∠B=30°,
P是BC边上的
动点,
则AP的长不可能是
( ).
A.3.5
B.4.2
C.5.8
D.7
图1-Z-2
D
【要点指导】判定两个直角三角形全等时,
除了可以应用一般三角形
全等的判定方法外,
还可以应用“斜边、直角边”定理,
即斜边和一条直角
边对应相等的两个直角三角形全等(HL).
“斜边、直角边”定理仅适用于
判定两个直角三角形全等.
角平分线的性质与判定定理均是由证明两个直
角三角形全等得到的.
角平分线的性质又可以为判定两个直角三角形全等
提供条件.
专题二
直角三角形全等的判定及角平分线的性质与判定
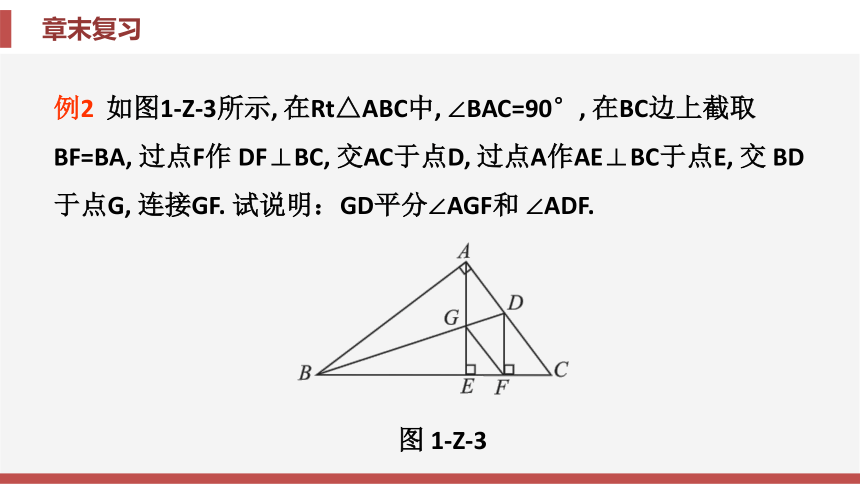
例2
如图1-Z-3所示,
在Rt△ABC中,
∠BAC=90°,
在BC边上截取BF=BA,
过点F作
DF⊥BC,
交AC于点D,
过点A作AE⊥BC于点E,
交
BD于点G,
连接GF.
试说明:GD平分∠AGF和
∠ADF.
图
1-Z-3
解:在Rt△BAD和Rt△BFD中,
BA=BF,
BD=BD,
∴Rt△BAD≌Rt△BFD(HL),
∴DA=DF,
∠BDA=∠BDF.
又∵GD=GD,
∴△AGD≌△FGD(SAS),
∴∠AGD=∠FGD,
∴GD平分∠AGF和∠ADF
相关题2
如图1-Z-4,
E是∠AOB
的平分线上的点,
EC⊥
OA,
ED⊥OB,
垂足分别
是C,
D.
(1)∠
EDC和
∠
ECD相
等吗?
(2)OC和OD相等吗?
(3)OE是线段CD的垂直
平分线吗?
图1-Z-4
【要点指导】(1)勾股定理:直角三角形两直角边a,
b的平方和,
等于
斜边c的平方,
即a2
+b2
=c2
.
(2)勾股定理的逆定理:如果三角形的三条边长a,
b,
c满足关系:
a2
+
b2
=c2
,
那么这个三角形是直角三角形.
专题三
勾股定理及其逆定理
例3
如图1-Z-5所示,
在四边形ABCD中,
∠B=90°,
AB=6,
BC=8,
CD=24,
AD=26,
则四边形ABCD的面积是(
).
A.78
B.288
C.144
D.72
图1-Z-5
C
相关题3
如图1-Z-6所示,
将长
方形ABCD沿直线AE
折叠,
顶点D恰好落在
BC边上的点F处.
已知
CE=3
cm,
AB=8
cm,
求
图中阴影部分的面积.
图1-Z-6
[解析]
图中阴影部分由两个直角三角形组成,只需求出BF和CF的长,即可求得两个直角三角形的面积.利用折叠的性质,可将两个三角形的每条边长都用BF表示出来,从而运用勾股定理建立方程.
【要点指导】转化思想是数学中非常重要的思想方法,
它可以把复杂
的、较难解决的问题转化为简单的、较易解决的问题.
素养提升
专题一
转化思想
例1
将两块三角板按图1-Z-7所示的方式放置,
其中∠C=∠EDB=
90°,
∠A=45°,
∠E=30°,
AB=DE=6.
求重叠部分(四边形DBCF)的面积.
图1-Z-7
解:在Rt△ABC中,
∵∠A=45°,
∴AC=BC,
∴其斜边AB上的高为
AB=3,
∴S△ABC=
×6×3=9.
在Rt△DBE中,
DE=6,
∠E=30°,
设BD=x,
则BE=2x,
根据勾股定理,
得(2x)2
=x2
+62
,
解得x=2
或x=-2
(舍去),
∴BD=2
,
∴AD=6-2
.
在Rt△ADF中,
∵∠A=45°,
∴AD=DF=6-2
,
∴S△ADF=
AD·DF=
=24-12
,
∴S四边形DBCF=S△ABC-S△ADF=9-(24-12
)=12
-15.
故重叠部分的面积为12
-15.
相关题
1
已知某开发区有一块四
边形的空地ABCD,
如图
1-Z-8所示,
现计划在该
空地上种上草皮.
经测
量,
∠A=90°,
AB=3
m,
BC=12
m,
CD=13
m,
DA=4
m,
若每平方米草
皮需要200元,
则需要投
入多少元?
图1-Z-8
[解析]
本题的实质是求四边形ABCD的面积,因为四边形ABCD不是规则图形,故连接BD,将其转化为两个三角形再计算.
【要点指导】分类讨论思想是指当被研究的问题包含多种可能情况,
且又不能一概而论时,
必须按可能出现的所有情况分别讨论,
得出各种情
况下相应的结论.
分类讨论应遵循的基本原则:不重复、不遗漏任何一种
可能情况,
每种可能情况都要按照同一标准进行讨论.
专题二
分类讨论思想
例2
如图1-Z-9所示,
一只蚂蚁从实心长方体
的顶点A出发,
沿长方体的表面爬行到对角顶点C1处,
怎样爬行路线最短?最短路线的长度为多少?
图1-Z-9
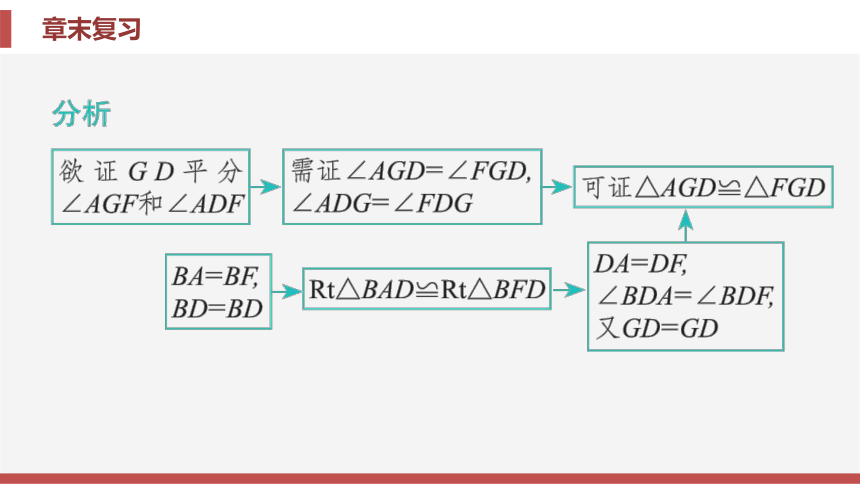
分析
首先将蚂蚁爬行的路线转化到同一平面上,
有三种情况,
由勾股定理分别求出三种情况下的路线长度,
比较后即可确定
蚂蚁爬行的最短路线的长.
解:第一种路线:
如图1-Z-10①所示,
沿AC1爬行.
在Rt△ABC1中,
∵AB=4,
BC1=BB1+B1C1=1+2=3,
∴AC1=
=5.
图1-Z-10
第二种路线:如图1-Z-10②所示,
沿AC1爬行.
在Rt△ACC1中,
∵AB=4,
BC=2,
∴AC=6.
又∵CC1=1,
∴AC1=
图1-Z-10
第三种路线:如图1-Z-10③所示,
沿AC1爬行.
在Rt△AB1C1中,
∵AA1=1,
A1B1=4,
∴AB1=5.
又∵B1C1=2,
∴AC1=
∵
∴按第一种方法爬行路线最短,
最短路线的长度为5.
图1-Z-10
相关题2-1
已知直角三角形的两边
长分别为
和
,
则斜
边上的高为__________.
相关题2-2
在△ABC中,
AB
=
1
5
,
AC=13,
高AD=12,
求
△ABC的周长.
认真观察图形,
注意分类讨论,
以防漏解.
[解析]由于根据已知条件不能确定△ABC是锐角三角形还是钝角三角形,故应分类讨论.
【要点指导】利用方程思想解决几何计算题的一般思路:先设所求
线段的长度或角度为未知数,
并设法把其他相关的量(线段的长度或角度)
用含有未知数的代数式表示出来,
再根据题意找出各个量之间存在的等量
关系,
然后代入其中建立方程(组),
通过解方程(组)求出所求线段的长度或
角度..
专题三
方程思想
例3
在长方形纸片ABCD中,
AD=4
cm,
AB=10
cm,
按图1-Z-11所示方式折叠,
使点B与点D重合,
折痕为EF,
求DE的长.
图1-Z-11
分析
根据勾股定理建立方程求解.
解:
设DE=x
cm,
则BE=DE=x
cm,
AE=AB-BE=(10-x)cm.
在Rt△ADE中,
DE2
=AE2
+AD2
,
即x2
=(10-x)2
+42
,
解得x=
.
故DE的长为
cm.
相关题3
[盘锦中考]校车安全是
近几年社会关注的热点
问题,
安全隐患主要是超
速和超载.
某中学九年
级数学活动小组进行了
测试汽车速度的试验.
如
图1-Z-12,
先在笔直的
公路l旁选取一点A,
在公
路l上确定两点B,
C,
使得
AC⊥l,
∠BAC=60°,
再
在AC上确定点D,
使得
∠BDC=75°,
AD=40米.
已
知本路段对校车限速
是50千米/时,
测得
某校
车从点B到点C匀速行驶
用时10秒.
图1-Z-12
(1)求CD的长(结果保留
根号);
(2)这辆校车在本路段
是否超速?请说明理由
(参考数据:
≈1.414,
≈1.732).
图1-Z-12
【要点指导】截长补短法是初中数学几何题中一种辅助线的添加方
法,
也是把几何问题化难为易的一种思想方法.
截长:(1)过某一点作长边的垂线;(2)在长边上截取一条与某一短边
相等的线段,
再证剩下的线段与另一短边相等.
补短:(1)延长短边;(2)通过旋转等方式使两短边拼合在一起.
当题目条件中存在“角平分线”这一信息时,
常常考虑是否可以用截
长补短的方法解决问题.
专题四
截长补短法
例4
已知:如图1-Z-13,
在四边形ABCD中,
BC>AB,
AD=DC,
BD平
分∠ABC.
求证:∠BAD+∠BCD=180°.
图1-Z-13
分析
因为平角等于180°,
因而考虑把两个不在一起的角通过全等转化
到一起,
组成平角.
图中缺少全等的三角形,
因而解题的关键在于构造全等三
角形,
可通过“截长补短法”来实现.
证明:过点D作DE⊥BA,
交BA的延长线于点E,
作DF⊥BC于点F,
如图
1-Z-14.
∵BD平分∠ABC,
∴DE=DF.
在Rt△ADE与Rt△CDF中,
DE=DF,
A
D
=DC,
∴Rt△ADE≌Rt△CDF(HL),
∴∠DAE=∠DCF.
又∵∠BAD+∠DAE=180°,
∴∠BAD+∠DCF=180°,
即∠BAD+∠BCD=180°.
图1-Z-14
相关题4
如图1-Z-15,
AD∥BC,
点E在线段AB上,
DE,
CE
分别为∠ADC,
∠BCD的
平分线.
求证:CD=AD+BC.
图1-Z-15
中考链接
母题1
(教材P7习题1.1A组第1题)
如
图
1
-
Z
-
1
6
,
CD是
R
t
△
A
B
C
的
中
线
,
∠ACB=90°,
∠CDA=120°,
求∠B的度数.
考点:直角三角形斜边上的中线等于斜边的
一半.
考情:中考中在选择题、填空题、解答题中均
有呈现,
通常用于计算线段的长度.
策略:直角三角形中,
斜边上的中线等于斜边的
一半,
体现了斜边与斜边上中线的数量关系.
常
利用该性质与勾股定理求直角边的长.
链接1
[大连中考]如图1-Z-17,
在Rt△ABC
中,
∠ACB=90°,
CD⊥AB,
垂足为D,
E是AB的中点,
CD=DE=a,
则AB的长为( )
A.2a
B.
C.3a
D.
B
分析
∵CD⊥AB,
CD=DE=a,
∴CE=
a.
∵在Rt△ABC中,
∠ACB=90°,
E是AB的中点,
∴AB=2CE=
.
母题2
(教材P7习题1.1A组第3题)
如图1
-
Z
-
1
8
,
线段
A
E与
B
C相交于点
D
,
BD=CD,
AD=ED,
CA⊥AE
,
∠1=30°,
且AB=3
cm,
那么线段BE多长呢?
考点:直角三角形中,
30°角所对的直角边等于
斜边的一半.
考情:直角三角形的性质是中考必考的知识点,
通常利用该性质来求线段的长度.
本知识点常与
其他知识点综合考查,
在选择题、填空题、解答
题中均有呈现.
策略:将30°角置于直角三角形中,
利用已知条
件求出30°角所对的直角边或斜边的长度,
为其
他计算准备条件.
链接2
[毕节中考]如图1-Z-
19,
在Rt△ABC中,
∠A=30°,
DE垂
直平分斜边AC,
交AB于点D,
E为垂
足,
连接CD.
若BD=1,
则AC的长为
(
).
A.2
B.2
C.4
D.4
A
母题3
(教材P13练习第2题)
如图1-Z-20,
AE是位于公路边的电线杆,
高
为12
m,
为了使电线CDE不影响汽车的正常行驶,
电力部门在公路的另一边竖立了一根高为6
m的
水泥撑杆BD,
用于撑起电
线.
已知两根杆子之间的
距离为8
m,
电
线CD与水平线AC的夹角为60°.
求
电
线CDE的总长L(A,
B,
C三点在同一直线
上,
电线
杆、水泥杆的粗细忽略不计).
考点:在直角三角形中,
两直角边的平方和等于
斜边的平方,
即
a2
+b2
=c2
.
考情:勾股定理反映了直角三角形中三边之间的
数量关系,
是几何计算的一个重要工具.
在中考
解答题,
尤其是综合题中常考不衰.
策略:在直角三角形中,
已知任意两边长,
可求
出第三边的长.
当其中某些边的长度未知时,
可
利用已知条件设未知数x,
用含x的代数式表示未
知边的长度,
再利用勾股定理建立方程求解.
链接3
[湘潭中考]《九章算
术》是我国古代的数学著作之一,
在
“勾股”章中记载了一道“折竹抵
地”问题:“今有竹高一丈,
末折抵
地,
去本三尺,
问折者高几何?”
翻
译成数学问题是:如图1-Z-21所示,
在Rt△ABC
中,
∠ACB=90°,
AC+AB=10,
BC=3,
求AC的长.
如
果设AC=x,
则可列
方程为_______________.
x2
+32
=(10-x)2
分析
设AC=x,
∵AC+AB=10,
∴AB=10-x.
∵在Rt△ABC中,
∠ACB=90°,
∴AC2
+BC2
=AB2
,
即x2
+32
=(10-x)2
.
链接4
[安顺中考]如图1-Z-22,
有两棵树,
一棵高10米,
另一棵高4米,
两树相距8米.一只小
鸟从一棵树的树梢飞到另一棵树的树梢,
则小鸟至
少飞行(
).
A.8米
B.10米
C.12米
D.14米
B
母题4
(教材P29复习题1B组第10题)
如图1-Z-24,
在△ABC中,
∠C=90°,
AC=BC,
AD是∠BAC的平分线且交BC于点D,
DE⊥AB,
垂
足为E.
若AB=12
cm,
求△DEB的周长.
考点:角平分线的性质.
考情:角平分线常与直角三角形的全等结合起
来考查,
在选择题、填空题、解答题中均有呈现.
常利用它们证明角(边)相等或求角(边)的大小.
策略:综合运用角平分线的性质和勾股定理解
决问题.
链接5
[常德中考]如图
1-Z-25,
已知BD是Rt△ABC的
角平分线,
ED是BC的垂直平分
线,
∠BAC=90°,
AD=3,
则CE的
长为( ).
A.6
B.5
C.4
D.3
D
分析
∵ED是BC的垂直平分线,
∴BE=CE,
BD=DC,
∴∠C=∠DBC.
∵BD是△ABC的角平分线,
∴∠ABD=∠DBC,
∴∠C=∠DBC=∠ABD=30°,
∴BC=2AB,
BD=2AD=6,
∴CE=AB=
链接6
[湘西州中考]如图1
-
Z
-
26,
在
Rt△ABC中,
∠C=90°,
AD平分∠CAB,
DE⊥AB于
点E,
若AC=6,
BC=8,
CD=3.
(1)求DE的长;
(2)求△ADB的面积.
解:
(1)∵AD平分∠CAB,
DE⊥AB,
∠C=90°,
∴CD=DE.
∵CD=3,
∴DE=3.
(
2
)
在
R
t
△
ABC中,
由勾股定理,
得
AB=
=10,
∴S△ADB=
AB·DE=
×10×3=15.
谢
谢
观
看!
第1章
直角三角形
章末复习
第1章
直角三角形
章末复习
知识框架
归纳整合
素养提升
中考链接
知识框架
性质
性质定理
判定定理
角的平分线
SSS,
SAS,
AAS,
ASA,
HL
直角三角形
全等的判定
直角三
角形
有两个角互余的三角形
一边上的中线等于这条边的
一半的三角形是直角三角形
判定
两直角边的平方和等于斜边的平方
较短两边的平方和等于最长边的
平方的三角形是直角三角形
勾股定理及
其逆定理
两锐角互余
30°角所对的直角边等于
斜边的一半
性质
斜边上的中线等于斜边的一半
一直角边等于斜边的一半,
此直角边所对的角为30°
【要点指导】直角三角形的性质:①两锐角互余;②斜边上的中线等
于斜边的一半;③30°角所对的直角边等于斜边的一半;④若某直角边等于
斜边的一半,
则该直角边所对的锐角为30°.
解题时需灵活运用以上性质.
归纳整合
专题一
直角三角形的相关性质
例1
如图1-Z-1,
在Rt△ABC中,
∠ACB=90°,
∠A=30°,
CD⊥AB,
垂足
为D.
求证:BD=
AD
图1-Z-1
证明:
∵CD⊥AB,
∠ACB=90°,
∴∠A+∠B=90°,
∠B+∠BCD=90°,
∴∠A=∠BCD.
∵∠A=30°,
∴∠BCD=30°,
∴BC=2BD.
∵∠A=30°,
∠ACB=90°,
∴AB=2BC,
∴AB=4BD.
∵AB=AD+BD,
∴AD=3BD,
∴BD=
AD.
相关题1
如图1-Z-2,
在Rt△ABC
中,
∠C=90°,
AC=3,
∠B=30°,
P是BC边上的
动点,
则AP的长不可能是
( ).
A.3.5
B.4.2
C.5.8
D.7
图1-Z-2
D
【要点指导】判定两个直角三角形全等时,
除了可以应用一般三角形
全等的判定方法外,
还可以应用“斜边、直角边”定理,
即斜边和一条直角
边对应相等的两个直角三角形全等(HL).
“斜边、直角边”定理仅适用于
判定两个直角三角形全等.
角平分线的性质与判定定理均是由证明两个直
角三角形全等得到的.
角平分线的性质又可以为判定两个直角三角形全等
提供条件.
专题二
直角三角形全等的判定及角平分线的性质与判定
例2
如图1-Z-3所示,
在Rt△ABC中,
∠BAC=90°,
在BC边上截取BF=BA,
过点F作
DF⊥BC,
交AC于点D,
过点A作AE⊥BC于点E,
交
BD于点G,
连接GF.
试说明:GD平分∠AGF和
∠ADF.
图
1-Z-3
解:在Rt△BAD和Rt△BFD中,
BA=BF,
BD=BD,
∴Rt△BAD≌Rt△BFD(HL),
∴DA=DF,
∠BDA=∠BDF.
又∵GD=GD,
∴△AGD≌△FGD(SAS),
∴∠AGD=∠FGD,
∴GD平分∠AGF和∠ADF
相关题2
如图1-Z-4,
E是∠AOB
的平分线上的点,
EC⊥
OA,
ED⊥OB,
垂足分别
是C,
D.
(1)∠
EDC和
∠
ECD相
等吗?
(2)OC和OD相等吗?
(3)OE是线段CD的垂直
平分线吗?
图1-Z-4
【要点指导】(1)勾股定理:直角三角形两直角边a,
b的平方和,
等于
斜边c的平方,
即a2
+b2
=c2
.
(2)勾股定理的逆定理:如果三角形的三条边长a,
b,
c满足关系:
a2
+
b2
=c2
,
那么这个三角形是直角三角形.
专题三
勾股定理及其逆定理
例3
如图1-Z-5所示,
在四边形ABCD中,
∠B=90°,
AB=6,
BC=8,
CD=24,
AD=26,
则四边形ABCD的面积是(
).
A.78
B.288
C.144
D.72
图1-Z-5
C
相关题3
如图1-Z-6所示,
将长
方形ABCD沿直线AE
折叠,
顶点D恰好落在
BC边上的点F处.
已知
CE=3
cm,
AB=8
cm,
求
图中阴影部分的面积.
图1-Z-6
[解析]
图中阴影部分由两个直角三角形组成,只需求出BF和CF的长,即可求得两个直角三角形的面积.利用折叠的性质,可将两个三角形的每条边长都用BF表示出来,从而运用勾股定理建立方程.
【要点指导】转化思想是数学中非常重要的思想方法,
它可以把复杂
的、较难解决的问题转化为简单的、较易解决的问题.
素养提升
专题一
转化思想
例1
将两块三角板按图1-Z-7所示的方式放置,
其中∠C=∠EDB=
90°,
∠A=45°,
∠E=30°,
AB=DE=6.
求重叠部分(四边形DBCF)的面积.
图1-Z-7
解:在Rt△ABC中,
∵∠A=45°,
∴AC=BC,
∴其斜边AB上的高为
AB=3,
∴S△ABC=
×6×3=9.
在Rt△DBE中,
DE=6,
∠E=30°,
设BD=x,
则BE=2x,
根据勾股定理,
得(2x)2
=x2
+62
,
解得x=2
或x=-2
(舍去),
∴BD=2
,
∴AD=6-2
.
在Rt△ADF中,
∵∠A=45°,
∴AD=DF=6-2
,
∴S△ADF=
AD·DF=
=24-12
,
∴S四边形DBCF=S△ABC-S△ADF=9-(24-12
)=12
-15.
故重叠部分的面积为12
-15.
相关题
1
已知某开发区有一块四
边形的空地ABCD,
如图
1-Z-8所示,
现计划在该
空地上种上草皮.
经测
量,
∠A=90°,
AB=3
m,
BC=12
m,
CD=13
m,
DA=4
m,
若每平方米草
皮需要200元,
则需要投
入多少元?
图1-Z-8
[解析]
本题的实质是求四边形ABCD的面积,因为四边形ABCD不是规则图形,故连接BD,将其转化为两个三角形再计算.
【要点指导】分类讨论思想是指当被研究的问题包含多种可能情况,
且又不能一概而论时,
必须按可能出现的所有情况分别讨论,
得出各种情
况下相应的结论.
分类讨论应遵循的基本原则:不重复、不遗漏任何一种
可能情况,
每种可能情况都要按照同一标准进行讨论.
专题二
分类讨论思想
例2
如图1-Z-9所示,
一只蚂蚁从实心长方体
的顶点A出发,
沿长方体的表面爬行到对角顶点C1处,
怎样爬行路线最短?最短路线的长度为多少?
图1-Z-9
分析
首先将蚂蚁爬行的路线转化到同一平面上,
有三种情况,
由勾股定理分别求出三种情况下的路线长度,
比较后即可确定
蚂蚁爬行的最短路线的长.
解:第一种路线:
如图1-Z-10①所示,
沿AC1爬行.
在Rt△ABC1中,
∵AB=4,
BC1=BB1+B1C1=1+2=3,
∴AC1=
=5.
图1-Z-10
第二种路线:如图1-Z-10②所示,
沿AC1爬行.
在Rt△ACC1中,
∵AB=4,
BC=2,
∴AC=6.
又∵CC1=1,
∴AC1=
图1-Z-10
第三种路线:如图1-Z-10③所示,
沿AC1爬行.
在Rt△AB1C1中,
∵AA1=1,
A1B1=4,
∴AB1=5.
又∵B1C1=2,
∴AC1=
∵
∴按第一种方法爬行路线最短,
最短路线的长度为5.
图1-Z-10
相关题2-1
已知直角三角形的两边
长分别为
和
,
则斜
边上的高为__________.
相关题2-2
在△ABC中,
AB
=
1
5
,
AC=13,
高AD=12,
求
△ABC的周长.
认真观察图形,
注意分类讨论,
以防漏解.
[解析]由于根据已知条件不能确定△ABC是锐角三角形还是钝角三角形,故应分类讨论.
【要点指导】利用方程思想解决几何计算题的一般思路:先设所求
线段的长度或角度为未知数,
并设法把其他相关的量(线段的长度或角度)
用含有未知数的代数式表示出来,
再根据题意找出各个量之间存在的等量
关系,
然后代入其中建立方程(组),
通过解方程(组)求出所求线段的长度或
角度..
专题三
方程思想
例3
在长方形纸片ABCD中,
AD=4
cm,
AB=10
cm,
按图1-Z-11所示方式折叠,
使点B与点D重合,
折痕为EF,
求DE的长.
图1-Z-11
分析
根据勾股定理建立方程求解.
解:
设DE=x
cm,
则BE=DE=x
cm,
AE=AB-BE=(10-x)cm.
在Rt△ADE中,
DE2
=AE2
+AD2
,
即x2
=(10-x)2
+42
,
解得x=
.
故DE的长为
cm.
相关题3
[盘锦中考]校车安全是
近几年社会关注的热点
问题,
安全隐患主要是超
速和超载.
某中学九年
级数学活动小组进行了
测试汽车速度的试验.
如
图1-Z-12,
先在笔直的
公路l旁选取一点A,
在公
路l上确定两点B,
C,
使得
AC⊥l,
∠BAC=60°,
再
在AC上确定点D,
使得
∠BDC=75°,
AD=40米.
已
知本路段对校车限速
是50千米/时,
测得
某校
车从点B到点C匀速行驶
用时10秒.
图1-Z-12
(1)求CD的长(结果保留
根号);
(2)这辆校车在本路段
是否超速?请说明理由
(参考数据:
≈1.414,
≈1.732).
图1-Z-12
【要点指导】截长补短法是初中数学几何题中一种辅助线的添加方
法,
也是把几何问题化难为易的一种思想方法.
截长:(1)过某一点作长边的垂线;(2)在长边上截取一条与某一短边
相等的线段,
再证剩下的线段与另一短边相等.
补短:(1)延长短边;(2)通过旋转等方式使两短边拼合在一起.
当题目条件中存在“角平分线”这一信息时,
常常考虑是否可以用截
长补短的方法解决问题.
专题四
截长补短法
例4
已知:如图1-Z-13,
在四边形ABCD中,
BC>AB,
AD=DC,
BD平
分∠ABC.
求证:∠BAD+∠BCD=180°.
图1-Z-13
分析
因为平角等于180°,
因而考虑把两个不在一起的角通过全等转化
到一起,
组成平角.
图中缺少全等的三角形,
因而解题的关键在于构造全等三
角形,
可通过“截长补短法”来实现.
证明:过点D作DE⊥BA,
交BA的延长线于点E,
作DF⊥BC于点F,
如图
1-Z-14.
∵BD平分∠ABC,
∴DE=DF.
在Rt△ADE与Rt△CDF中,
DE=DF,
A
D
=DC,
∴Rt△ADE≌Rt△CDF(HL),
∴∠DAE=∠DCF.
又∵∠BAD+∠DAE=180°,
∴∠BAD+∠DCF=180°,
即∠BAD+∠BCD=180°.
图1-Z-14
相关题4
如图1-Z-15,
AD∥BC,
点E在线段AB上,
DE,
CE
分别为∠ADC,
∠BCD的
平分线.
求证:CD=AD+BC.
图1-Z-15
中考链接
母题1
(教材P7习题1.1A组第1题)
如
图
1
-
Z
-
1
6
,
CD是
R
t
△
A
B
C
的
中
线
,
∠ACB=90°,
∠CDA=120°,
求∠B的度数.
考点:直角三角形斜边上的中线等于斜边的
一半.
考情:中考中在选择题、填空题、解答题中均
有呈现,
通常用于计算线段的长度.
策略:直角三角形中,
斜边上的中线等于斜边的
一半,
体现了斜边与斜边上中线的数量关系.
常
利用该性质与勾股定理求直角边的长.
链接1
[大连中考]如图1-Z-17,
在Rt△ABC
中,
∠ACB=90°,
CD⊥AB,
垂足为D,
E是AB的中点,
CD=DE=a,
则AB的长为( )
A.2a
B.
C.3a
D.
B
分析
∵CD⊥AB,
CD=DE=a,
∴CE=
a.
∵在Rt△ABC中,
∠ACB=90°,
E是AB的中点,
∴AB=2CE=
.
母题2
(教材P7习题1.1A组第3题)
如图1
-
Z
-
1
8
,
线段
A
E与
B
C相交于点
D
,
BD=CD,
AD=ED,
CA⊥AE
,
∠1=30°,
且AB=3
cm,
那么线段BE多长呢?
考点:直角三角形中,
30°角所对的直角边等于
斜边的一半.
考情:直角三角形的性质是中考必考的知识点,
通常利用该性质来求线段的长度.
本知识点常与
其他知识点综合考查,
在选择题、填空题、解答
题中均有呈现.
策略:将30°角置于直角三角形中,
利用已知条
件求出30°角所对的直角边或斜边的长度,
为其
他计算准备条件.
链接2
[毕节中考]如图1-Z-
19,
在Rt△ABC中,
∠A=30°,
DE垂
直平分斜边AC,
交AB于点D,
E为垂
足,
连接CD.
若BD=1,
则AC的长为
(
).
A.2
B.2
C.4
D.4
A
母题3
(教材P13练习第2题)
如图1-Z-20,
AE是位于公路边的电线杆,
高
为12
m,
为了使电线CDE不影响汽车的正常行驶,
电力部门在公路的另一边竖立了一根高为6
m的
水泥撑杆BD,
用于撑起电
线.
已知两根杆子之间的
距离为8
m,
电
线CD与水平线AC的夹角为60°.
求
电
线CDE的总长L(A,
B,
C三点在同一直线
上,
电线
杆、水泥杆的粗细忽略不计).
考点:在直角三角形中,
两直角边的平方和等于
斜边的平方,
即
a2
+b2
=c2
.
考情:勾股定理反映了直角三角形中三边之间的
数量关系,
是几何计算的一个重要工具.
在中考
解答题,
尤其是综合题中常考不衰.
策略:在直角三角形中,
已知任意两边长,
可求
出第三边的长.
当其中某些边的长度未知时,
可
利用已知条件设未知数x,
用含x的代数式表示未
知边的长度,
再利用勾股定理建立方程求解.
链接3
[湘潭中考]《九章算
术》是我国古代的数学著作之一,
在
“勾股”章中记载了一道“折竹抵
地”问题:“今有竹高一丈,
末折抵
地,
去本三尺,
问折者高几何?”
翻
译成数学问题是:如图1-Z-21所示,
在Rt△ABC
中,
∠ACB=90°,
AC+AB=10,
BC=3,
求AC的长.
如
果设AC=x,
则可列
方程为_______________.
x2
+32
=(10-x)2
分析
设AC=x,
∵AC+AB=10,
∴AB=10-x.
∵在Rt△ABC中,
∠ACB=90°,
∴AC2
+BC2
=AB2
,
即x2
+32
=(10-x)2
.
链接4
[安顺中考]如图1-Z-22,
有两棵树,
一棵高10米,
另一棵高4米,
两树相距8米.一只小
鸟从一棵树的树梢飞到另一棵树的树梢,
则小鸟至
少飞行(
).
A.8米
B.10米
C.12米
D.14米
B
母题4
(教材P29复习题1B组第10题)
如图1-Z-24,
在△ABC中,
∠C=90°,
AC=BC,
AD是∠BAC的平分线且交BC于点D,
DE⊥AB,
垂
足为E.
若AB=12
cm,
求△DEB的周长.
考点:角平分线的性质.
考情:角平分线常与直角三角形的全等结合起
来考查,
在选择题、填空题、解答题中均有呈现.
常利用它们证明角(边)相等或求角(边)的大小.
策略:综合运用角平分线的性质和勾股定理解
决问题.
链接5
[常德中考]如图
1-Z-25,
已知BD是Rt△ABC的
角平分线,
ED是BC的垂直平分
线,
∠BAC=90°,
AD=3,
则CE的
长为( ).
A.6
B.5
C.4
D.3
D
分析
∵ED是BC的垂直平分线,
∴BE=CE,
BD=DC,
∴∠C=∠DBC.
∵BD是△ABC的角平分线,
∴∠ABD=∠DBC,
∴∠C=∠DBC=∠ABD=30°,
∴BC=2AB,
BD=2AD=6,
∴CE=AB=
链接6
[湘西州中考]如图1
-
Z
-
26,
在
Rt△ABC中,
∠C=90°,
AD平分∠CAB,
DE⊥AB于
点E,
若AC=6,
BC=8,
CD=3.
(1)求DE的长;
(2)求△ADB的面积.
解:
(1)∵AD平分∠CAB,
DE⊥AB,
∠C=90°,
∴CD=DE.
∵CD=3,
∴DE=3.
(
2
)
在
R
t
△
ABC中,
由勾股定理,
得
AB=
=10,
∴S△ADB=
AB·DE=
×10×3=15.
谢
谢
观
看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
