江苏省无锡市2019-2020学年度第一学期七年级数学第6章 平面图形的认识(一)的专题复习学案含答案
文档属性
| 名称 | 江苏省无锡市2019-2020学年度第一学期七年级数学第6章 平面图形的认识(一)的专题复习学案含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 347.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 08:22:55 | ||
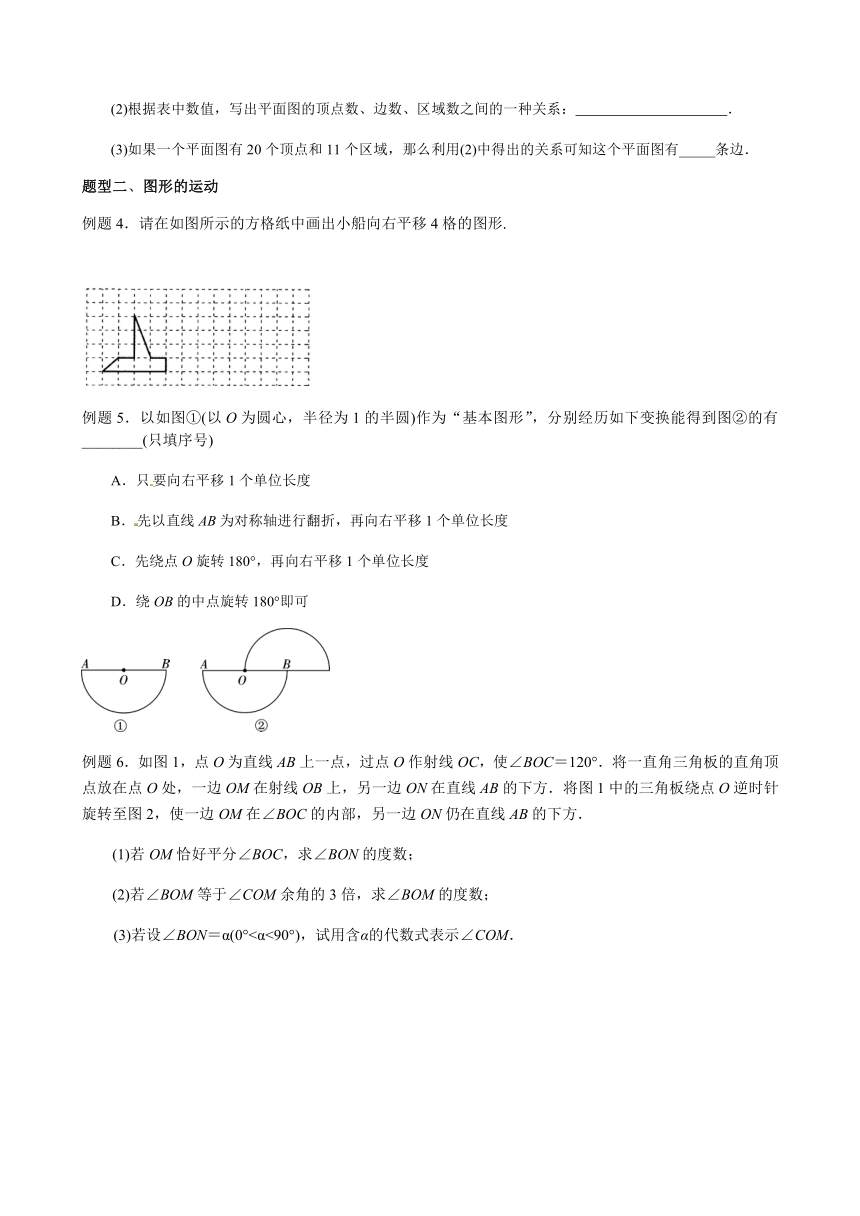
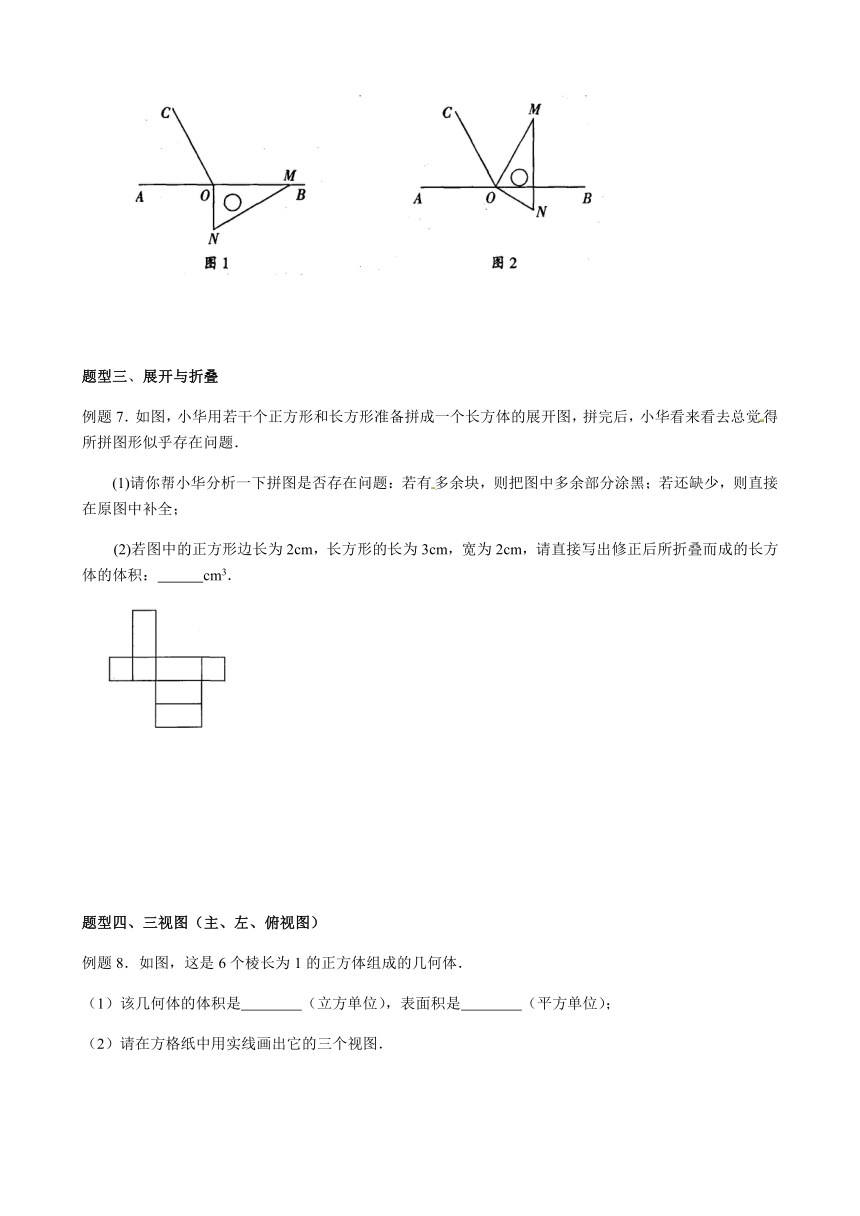
图片预览



文档简介
初一数学平面图形的专题复习
【学习目标】
复习本学期所学的图形的运动、展开与折叠、三视图、直线、射线、线段、角、平行与垂直等相关知识。
【典型例题】
题型一、与图形有关的问题
例题1.如图,下列图形中,哪些是柱体? .
例题2.如图,一个3×2的长方形可以用2种不同的方式分割成3或6个正方形,那么一个4×2的长方形用不同方式分割后,正方形的个数可以是________.
或
例题3.如图,若将类似于①、②、③、④四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图②和表中对应的数值,探究计数的方法并作答.
(1) 数一数每个图中各有多少个顶点,有多少条边,这些边围出多少个区域,并填表:
图 ① ② ③ ④
顶点数(S) 7
边数(M) 9
区域数(N) 3
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系: .
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有_____条边.
题型二、图形的运动
例题4.请在如图所示的方格纸中画出小船向右平移4格的图形.
例题5.以如图①(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换能得到图②的有________(只填序号)
A.只要向右平移1个单位长度
B.先以直线AB为对称轴进行翻折,再向右平移1个单位长度
C.先绕点O旋转180°,再向右平移1个单位长度
D.绕OB的中点旋转180°即可
例题6.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,另一边ON仍在直线AB的下方.
(1)若OM恰好平分∠BOC,求∠BON的度数;
(2)若∠BOM等于∠COM余角的3倍,求∠BOM的度数;
(3)若设∠BON=α(0°<α<90°),试用含α的代数式表示∠COM.
题型三、展开与折叠
例题7.如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小华看来看去总觉得所拼图形似乎存在问题.
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全;
(2)若图中的正方形边长为2cm,长方形的长为3cm,宽为2cm,请直接写出修正后所折叠而成的长方体的体积: cm3.
题型四、三视图(主、左、俯视图)
例题8.如图,这是6个棱长为1的正方体组成的几何体.
(1)该几何体的体积是 (立方单位),表面积是 (平方单位);
(2)请在方格纸中用实线画出它的三个视图.
题型五、画图题
例题9.如图所示,按要求画图并回答问题:
(1) 画出图中△ABC的边AC上的高BD;(2) 过点D画边BA、BC的垂线,垂足分别是E、F;
(3) 写出点D到AB、BC的距离分别是哪条线段的长.
题型六、角的相关知识
例题10.用度、分、秒表示:(1) 78.36°=________;(2) °=________.
例题11.如图,射线表示的是北偏东15°方向,射线表示的是北偏西40°方向,,射线是的反向延长线.
(1)试确定射线表示的方向;(2)求的度数;(3)若射线平分,求的度数.
题型七、直线、射线、线段的相关知识
例题12.如图,已知AB=10cm,点C在直线AB上,如果BC=4cm,点D是线段AC的中点,求线段BD的长.
【变式1】如图,直线l上有AB两点,AB=12cm,点O是线段AB上的一点,OA=2OB.
(1)OA= cm OB= cm;
(2)若点C是线段AB上一点,且满足AC=CO+CB,求CO的长;
(3)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s.设运动时间为ts,当点P与点Q重合时,P,Q两点停止运动.
①当t为何值时,2OP—OQ=4;
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以3cm/s的速度向点P运动,遇到点P后再立即返回,以3cm/s的速度向点Q运动,如此往返,直到点P,Q停止时,点M也停止运动.在此过程中,点M行驶的总路程是多少?
【课后练习】
1.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
2.点在同一条数轴上,其中点表示的数分别为—3,1,若=2,则等于( )
A.3 B.2 C.3或5 D.2或6
3.把一个无盖的正方体盒子展开,下图中正确的有( )
A.1个 B.2个 C.3个 D.4
4.一个角的补角的余角等于这个角的,则这个角的度数为________°.
5.有一长为6 cm,宽为4 cm的长方形纸板,现以其一组对边中点所在直线为轴,绕其旋转一周,得到了一个几何体,那么这个几何体的体积是 .(结果保留)
6.如图,AB、CD相交于点O,OE是∠AOC的平分线,∠BOD=70°,∠EOF=65°,则∠AOF的度数为 °.
7.如图,A、B、C是网格图中的三点.
(1)作直线AB、射线AC、线段BC. (2)过B作AC的平行线BD.
(3)作出表示B到AC的距离的线段BE. (4)判断BD与BE的位置关系是 .
(5)线段BE与BC的大小关系是:BE BC(填“>”、“<”、“=”).
8.如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线.
(1)图中除了直角外,还有相等的角吗?请写出两对;
(2)如果∠DOA=60°,求∠COP与∠BOF的度数.
9. 线段AB=10,C是AB的中点.
(1)求线段BC的长;(2)若点D在直线AB上,DB=2.5,求线段CD的长.
10.在数学的学习过程中,我们要不断地归纳,思考和迁移,这样才能提高我们解决问题的能力:
规律发现:
在学完《数轴》这节课后,小明的作业有两道小题,请你帮他把余下的两空完成:
(1)点A表示的数是2,点B表示的数是6,则线段AB的中点C表示的数为 4 ;
(2)点A表示的数是5,点B表示的数是7,则线段AB的中点C表示的数为 ;
发现:点A表示的数是a,点B表示的数是b,则线段AB的中点C表示的数为 .
直接运用:
将数轴按如图(1)所示从某一点开始折出一个等边三角形ABC,设点A表示的数为x3,点B表示的数为2x+1,C表示的数为x1,则x的值为 ,若将△ABC从图中位置向右滚动,则数字2014对应的点将与△ABC的顶点 重合.
类比迁移:
如图(2),OB⊥OX, OA⊥OC,∠COX=30°,若射线OA绕O点每秒30°的速度顺时针旋转,射线OB绕O点每秒20°的速度顺时针旋转,射线OC以每秒10°的速度逆时针旋转,三线同时旋转,当一条射线与直线OX重合时,三条射线同时停止运动,问:运动几秒时,其中一条射线是另外两条射线夹角的平分线?
平面图形的专题复习
课后练习答案:
1.D
2.D
3.C
4.108°
5.36或24
6.30°
7.(1)— (3)略;(4)垂直;(5)<.
8.(1)有 ∠COP=∠BOP,∠COE=∠FOB,∠POE=∠FOP,∠COB=∠AOD.(2)∠COP=30°,∠BOF=30°.
9.解:(1)∵线段AB=10,C是AB的中点,
∴BC=AB=5;
(2)如图1,∵BC=5,BD=2.5,
∴CD=BC﹣CD=2.5;
如图2,∵BC=5,BD=2.5,
∴CD=BC+CD=7.5,
综上所述:线段CD的长为2.5或7.5.
10.解:(1)∵将数轴按如图所示从某一点开始折出一个等边三角形ABC,设点A表示的数为x﹣3,点B表示的数为2x+1,点C表示的数为x﹣1,
∴x﹣1﹣(2x+1)=2x+1﹣(x﹣3);
∴﹣2x=6,
解得:x=﹣3.
故A表示的数为:x﹣3=﹣3﹣3=﹣6,
点B表示的数为:2x+1=2×(﹣3)+1=﹣5,
即等边三角形ABC边长为1,
数字2014对应的点与﹣4的距离为:2014+4=2018,
∵2018÷3=672…2,C从出发到2014点滚动672周后再滚动两次,
∴数字2014对应的点将与△ABC的顶点B重合.
故答案为:﹣3,B;
(2)∵OB⊥OX,OA⊥OC,∠COX=30°,
∴∠AOB=30°,
经分析知2秒时OB与OC重合,所以在2秒以前设运动x1秒时,OB是OA与OC的角平分线,
30﹣10 x1=60﹣30 x1
解得x1=1.5.
经分析知2秒时OB与OC重合,2.25秒时OA与OC重合,所以在2秒到2.25秒间,OC是OA与OB的角平分线,设运动x2秒时,
30 x2﹣60=90﹣40 x2
x2=
3秒时OA与OB重合,所以在3秒以前设运动x3秒时,OA是OB与OC的角平分线,
30 x3+10 x3﹣90=20 x3+30﹣30 x3
解得x3=2.4.
4秒时与OA直线OX重合,设3秒后4秒前运动x4秒时OB是OA与OC的角平分线,
20 x4﹣60+10 x4=30 x4﹣30﹣20 x4
解得x4=1.5(舍去).
故运动1.5秒,秒或2.4秒时,其中一条射线是另外两条射线夹角的平分线.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
