13.5 平行线的性质 教案(共5课时)
文档属性
| 名称 | 13.5 平行线的性质 教案(共5课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 176.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 08:41:11 | ||
图片预览



文档简介
13.5平行线的性质(1)
教学目标:
1、通过观察,认识“两直线平行,同位角相等”这一基本事实;初步认识平行线的性质与平行线的判定的区别,并正确选择应用.
2、进一步体会几何说理的过程,学会正确书写证明过程,逐步培养逻辑推理能力,体会化归的数学思想..
教学重点:平行线性质的运用.
教学难点:平行线的性质与平行线的判定的区别.
教学过程:
平行线的性质1
引入:
师:利用同位角相等,可以判定两条直线平行.反过来,如果两条直线平行,同位角相等吗?
演示观察:
教师几何画板演示:(任意两条)平行线a、b被直线l(可动)所截,得同位角、,并测量、的大小.
3、平行线的性质1:
问:通过观察,你能得到什么结论?
平行线的性质1. 两条平行线被第三条直线所截,同位角相等.
简单的说就是:
两直线平行,同位角相等.
如何用符号语言表示这个性质?
(已知)
(两直线平行,同位角相等)
想一想:平行线的判定方法1和平行线的性质1有何区别?
小结:注意平行线的性质和平行线的判定的区别,在应用时正确选用,
若已知两直线平行,由它们的平行得出其他结论,是应用了平行线的性质;
若未知直线平行,而要说明其平行,则需应用平行线的判定.
二、平行线的性质1的应用
例题1 如图,已知直线a、b被直线l所截,a∥b,∠1=50°, 求∠2的度数.
(教师边读题,边在图中标注已知条件.)
问1:题中有哪些已知条件?
问2:已知a∥b,利用平行线的性质,你能得到什么结论?
问3:你说说怎样求出∠2的度数吗?
解:a∥b(已知),∠3=∠2(两直线平行,同位角相等).
∠1与∠3是对顶角,∠1=∠3(对顶角相等).
∠1=∠2(等量代换).
∠1=50°(已知),∠2=50°(等量代换).
小结:
1、题中若给出两直线平行的条件,则要考虑平行线的性质;
2、∠3作为中间量起到了桥梁作用.(类似的,也可找∠2的对顶角解题).
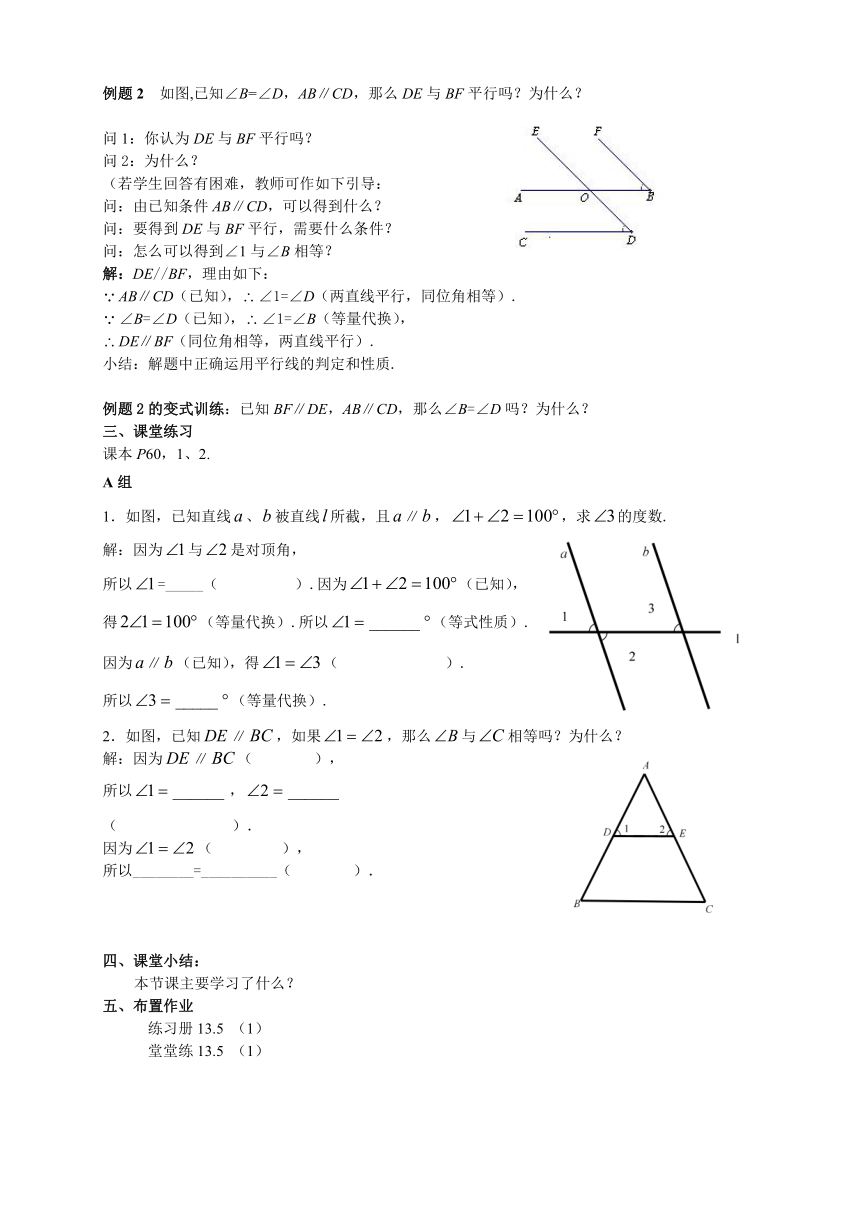
例题2 如图,已知∠B=∠D,AB∥CD,那么DE与BF平行吗?为什么?
问1:你认为DE与BF平行吗?
问2:为什么?
(若学生回答有困难,教师可作如下引导:
问:由已知条件AB∥CD,可以得到什么?
问:要得到DE与BF平行,需要什么条件?
问:怎么可以得到∠1与∠B相等?
解:DE//BF,理由如下:
AB∥CD(已知),∠1=∠D(两直线平行,同位角相等).
∠B=∠D(已知),∠1=∠B(等量代换),
DE∥BF(同位角相等,两直线平行).
小结:解题中正确运用平行线的判定和性质.
例题2的变式训练:已知BF∥DE,AB∥CD,那么∠B=∠D吗?为什么?
三、课堂练习
课本P60,1、2.
A组
1.如图,已知直线、被直线所截,且∥,,求的度数.
解:因为与是对顶角,
所以=_____( ).因为(已知),
得(等量代换).所以(等式性质).
因为∥(已知),得( ).
所以(等量代换).
2.如图,已知∥,如果,那么与相等吗?为什么?
解:因为∥( ),
所以,
( ).
因为( ),
所以________=__________( ).
四、课堂小结:
本节课主要学习了什么?
五、布置作业
练习册13.5 (1)
堂堂练13.5 (1)
13.5平行线的性质(2)
教学目标:
1.探求平行线的性质2、3的过程中,感受化归的数学思想,体会文字语言、图形语言、符号语言之间的互换.
2.在平行线的传递性的推导过程中,感受添加辅助线构造基本图形的策略.
3.通过平行线性质的运用,逐步提高分析能力与简单的逻辑推理能力.
教学重点及难点
重点:平行线性质2、3的运用.
难点:平行线传递性的探求.
教学过程:
一、复习引入
昨天学习了平行线的性质1,如何叙述?
师出示图形,问:如图,如何用符号语言表示?
引言:在学习平行线的判定方法时,我们学会了一种判定方法后,其他判定方法的学习都是通过将新知转化为旧知来解决问题的.现在我们知道了平行线的性质1:两直线平行,同位角相等.则一对内错角的大小之间有什么数量关系?一对同旁内角的大小之间又有什么数量关系呢?
揭示课题:平行线的性质(2)
二、归纳性质
1、如图,直线a、b被直线l所截,a∥b,问∠1与∠2大小有何关系?
师引导:运用学过的性质能否说明你的结论?
说理:a∥b(已知),
∠3=∠2(两直线平行,同位角相等).
又∠1=∠3(对顶角相等),
∠1=∠2(等量代换).
模仿平行线性质1能否说出平行线的性质2?
师补充:简单地说:就是两直线平行,内错角相等.
问:用符号语言如何表示?
2、如图:直线a、b被直线l所截,a∥b,
∠4与∠2这对同旁内角有何数量关系?
问:你能用学过的知识来说明你的结论是正确的吗?
说理:将∠3的邻补角记作∠4,
则∠3+∠4=1800(邻补角的意义)
a∥b(已知)
∠3=∠2(两直线平行,同位角相等)
∠4+∠2=1800(等量代换)
问:还有其他方法吗?
问:你能说出平行线的性质3吗?
问:用符号语言如何表示?
问:平行线的性质与判定有何区别?
教师总结:知道平行用性质;要证平行用判定.
三、实践运用
1、例题3:如图,已知AB∥CD,AD∥BC,那么(1)∠1与∠2相等吗?(2)∠3与∠4呢?
出示第一小问,教师引导方法:观察时只需∠1与∠2,把其他条件隐去.
问1:∠1与∠2是哪两条直线被谁所截得的什么角?
∠1与∠2相等吗?
出示第二小问,让学生分析解答过程.
问2:∠3与∠4哪两条直线被谁所截得的什么角?∠3与∠4相等吗?
【小结】对平行线性质的运用,前提要找到这些角是哪两条直线被哪条直线所截形成的.
2、例题4:如图,已知AB∥CD,AD∥BC,∠A=550,求∠C的度数.
问:根据已知条件,可直接得到哪些角的度数?
求∠C可以怎么思考?
说明:教师边说边勾出∠B或∠D的边进行分析.
解:AD∥BC(已知),
∠A+∠B=1800(两直线平行,同旁内角互补).
∠A=550(已知),
∠B=1800-550=1250(等式性质)
同理可得:∠C=550.
3、思考:如图,有三条直线a,b,c,已知a∥b,b∥c,这时直线a与c有怎样的位置关系?
师引导:要证平行,怎么办?启发学生说出需要同位角,内错角或同旁内角.或者启发学生发现需要三线八角这样的基本图形.
师:现在图形不满足条件,需要构造同位角.我们可以怎么构造?
请学生操作:添一条直线l,分别与a,b,c相交.
师引导分析:要说明a∥c,只要说明什么相等?
如何说理?
得到平行线的传递性:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
简单地说:平行于同一条直线的两条直线平行.
问:如何用符号语言表示?
四、 课堂练习,及时巩固
1、书P62:1、2
A组:
如图,已知直线AB、CD被直线AE所截,且AB∥CD.
(1)从∠1=115°,可以得到∠3是多少度?为什么? (2)从∠1=115°,可以得到∠2是多少度?为什么?
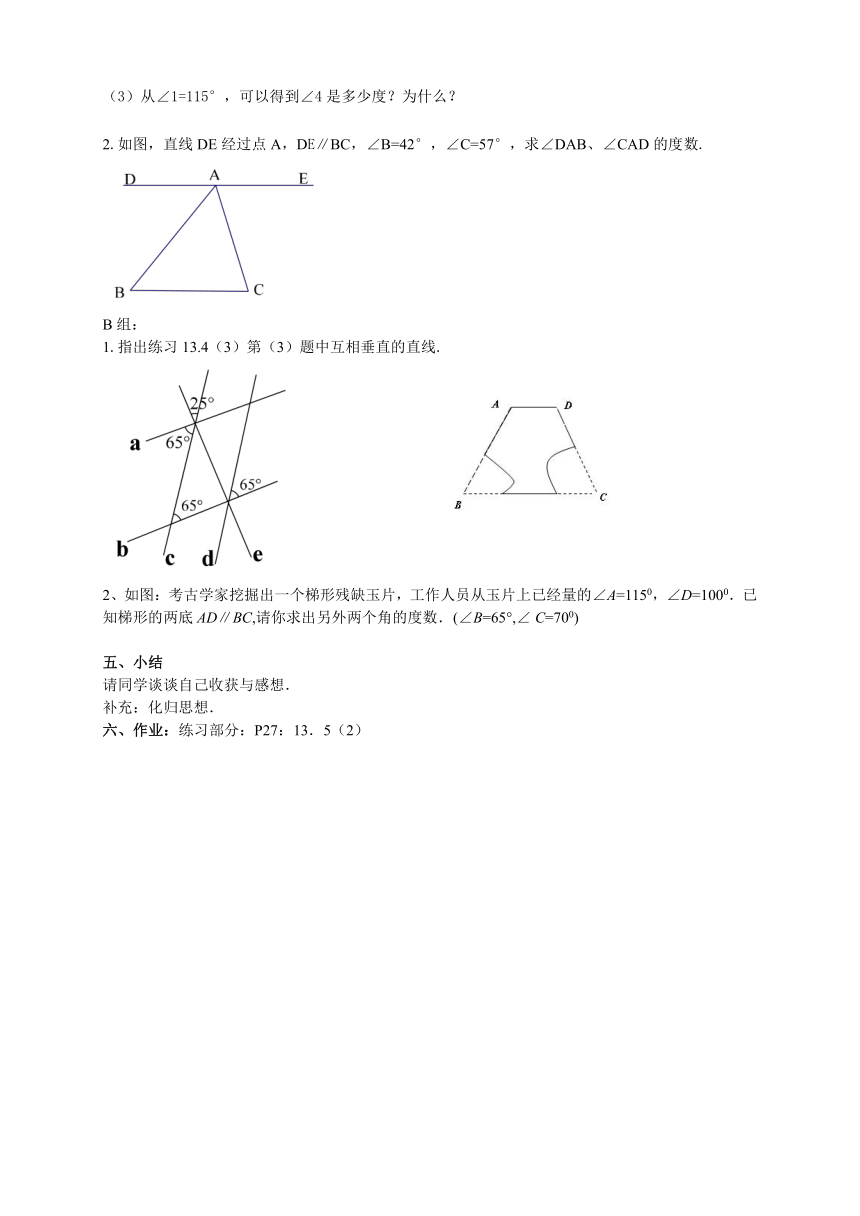
(3)从∠1=115°,可以得到∠4是多少度?为什么?
2.如图,直线DE经过点A,DE∥BC,∠B=42°,∠C=57°,求∠DAB、∠CAD的度数.
B组:
1.指出练习13.4(3)第(3)题中互相垂直的直线.
2、如图:考古学家挖掘出一个梯形残缺玉片,工作人员从玉片上已经量的∠A=1150,∠D=1000.已知梯形的两底AD∥BC,请你求出另外两个角的度数.(∠B=65°,∠ C=700)
五、小结
请同学谈谈自己收获与感想.
补充:化归思想.
六、作业:练习部分:P27:13.5(2)
13.5平行线的性质(3)
教学目标:
1.经历测量两条平行线中一直线上的点到另一直线的距离的操作过程,初步理解两条平行线间的距离的概念,体会从特殊到一般的研究问题方法.
2.通过图形的运动,体会平行线间的距离处处相等的初步应用,感受图形运动的数学思想.
教学重难点:
两条平行线间的距离意义及运用.
教学过程:
一、复习旧知,引入课题
复习:
1、什么是两点之间的距离?
2、什么是点到直线的距离?
3、什么是两条平行线之间的距离?
操作1:任意画两条互相平行的直线和:
(1)请同学们在直线上任意取5个点,
度量一下这5个点到直线的距离.
你能得到什么结论?(学号是单号的操作)
(2)请同学们在直线b上任意取5个点,这5个点到直线的距离都相等吗?(学号是双号的操作)
师:通过同学们动手操作度量,交流度量结果,发现了什么?
二、探究新知,讲授新课
两条平行线间的距离:
两条平行线中,任意一条直线上的所有点到另一条直线的距离都是一个定值,这个定值叫做这两条平行线间的距离.
师:概念的关键词是:
及时反馈 如图,已知AB//CD,AD//BC,交BC于点E,交CD与点F.
线段AE的长度是哪两条平行线间的距离?
如何度量AB、CD间的距离?
追问:还有没有其他的表示方法?
思考:如图:直线,点E、F、G、H是直线上的任意一点,
那么、的面积有什么特征?
追问:为什么高等?
与、的面积相等的三角形还有吗?
变式1:
如果我将上图线段AB沿直线a平移,
分别与点E、G构成的三角形面积还是相等的吗?为什么?
师追问:在上图中还有面积相等的三角形吗?
变式2: 如图:直线,点A、E、F在直线上,点B、C、D在直线b上,BC=EF, 与的面积相等吗?为什么?
师问1:你认为与的面积相等吗?
师问2:为什么?
追问:为什么高相等?
答:与的面积相等.
解:作AH1⊥b,垂足为点H1,
作DH2⊥a,垂足为点H2 ,
由,得AH1 = DH2 (平行线间距离的意义).
设和的面积为S1,S2.
∵S1=BCAH1(三角形面积公式),
S2 =EFDH2,
又∵ BC=EF(已知),
∴S1=S2(等量代换).
即:与的面积相等.
拓展:怎样能在这两条平行线间作出一个三角形,使它的面积是的2倍?
三、课堂练习
书P64:1、2
教师巡视,如发现问题,及时解决及指导.
A组
1.如图,直线,那么与
的面积相等吗?为什么?
2. 如图,已知点E、F分别在长方形ABCD的边AB、CD上,且AF//CE,请分别度量AE与CF之间的距离、AF与CE之间的距离(精确到0.1m)
B组
1. 已知:如图,在中,点D在边BC上,且,试说明
2.如图,已知AB//CD,AD//BC,点E是AD上的任一点,,求.(补充)
C组
已知:如图,直线,写出图中所有面积相等的三角形并说明理由.
四、课堂小结
通过这堂课,你学到了什么?
数学思想和方法:在探究平行线间距离的过程中感受从特殊到一般的归纳方法.
五、布置作业
《练习册》P29-30习题13.5(3)
§13.5平行线的性质(4)
教学目标:
1.准确运用平行线判定与性质解决简单的问题,逐步把握平行线的判定与性质之间的区别和联系.
2.进一步体会逻辑说理的方法,感受正确添加辅助线的方法,提高分析问题、解决问题的能力.
教学重点:运用平行线判定与性质解决简单的问题.
教学难点:平行线判定与性质的应用.
教学过程:
一、复习引入
问1:平行线的判定方法是什么?
问2:平行线的性质呢?
问3:平行线的判定与性质的区别是什么,如何正确选择?
【小结】
条件
结论
平行线的判定
角的关系
两直线平行
平行线的性质
两直线平行
角的关系
下面我们用平行线的判定和性质解决一些问题.
二、初步应用
例题1 如图:已知∠BAE=∠CAE,AE∥DB,试说明∠ABD=∠D的理由.
分析已知条件:
在图形中标∠BAD =∠1,∠CAD =∠2,∠ABE=∠3,
问1:由AD//BE可得哪些与∠E、∠3相关的结论?为什么?
问2:说明∠3=∠E还需要哪些条件?依据是什么?
解:∵AD∥BE(已知),
∴∠E=∠2(两直线平行,同位角相等),
∠1=∠3(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠3=∠E(等量代换).
例题2 如图:已知∠ABC=62°,∠1=∠2,求∠C的度数.
问1:已知条件中的关键条件是什么?可得什么结论?为什么?
问2:这里运用了平行线的判定方法,∠1和
∠2是哪两条直线被那条直线所截得到的内错角?
问3:有了平行线后,再利用平行线的性质可得到哪些与∠C相关的结论?为什么?
问4:现在如何求∠C的度数?
解:∵∠1=∠2 (已知),
∴AB∥CD(内错角相等,两直线平行),
∴∠ABC+∠C=180o(两直线平行,同旁内角互补).
∵∠ABC=62o(已知),
∴∠C=118o(等式性质).
*问5:能求∠A的度数吗?为什么?
三、拓展提高
例题3 如图,已知AB//CD,那么∠B+∠BED+∠D等于多少度?为什么?
j,
问1:你能猜测∠B+∠BED+∠D等于多少度吗?
问2:360°是两个180°的和。什么位置关系的角的数量关系会出现180°?
问3:我们需要有两组平行线构造出两对同旁内角,你会这样去构造出这两组平行线呢?
问4:如果过点E作EF//AB,有什么帮助吗?
问5:∠D+∠DEF如何求?为什么?
解:过点E作EF//AB,得∠B+∠BEF=180o(两直线平行,同旁内角互补).
因为AB//CD(已知),EF//AB(所作),
所以EF//CD(平行线的传递性).得∠D+∠DEF=180o(两平线平行,同旁内角互补).
因此∠B+∠BEF+∠DEF十∠D=360o,即∠B+∠BED+∠D=360o.
四、课堂练习
A组:
如图,已知AB∥CD,∠A=32°,∠B=68°,求∠BEF的度数.
2.如图,已知直线、被直线所截,∥且∠1=∠2=,求∠1、∠2的度数.
B组:如图,已知AB∥CD,,那么∠B、∠BED、∠D有怎样的数量关系?为什么?
五、课堂小结
谈谈这节课你有什么收获、体会或想法?
教师说明:解题过程中理解、体会图形语言、符号语言、数学语言的转化和合理应用.
六、布置作业
《练习册》习题13.5(4)
§13.5平行线的性质(5)
教学目标:
1.综合运用平行线的判定和性质解决问题,培养逻辑思维能力.
2.进一步了解说理的叙述和表达要求,体会几何说理的过程.
教学重点及难点:
平行线的判定和性质的综合运用.
教学过程:
一.复习引入:
师:我们知道由两条直线平行可以得到一些特殊角之间的数量关系,反之,也可以根据一些角度之间的数量关系来判断两条直线平行.
师:若已知两直线平行时,用什么定理?若已知两角之间的关系去判断平行,用什么定理?
思考:填空:如图,
① AD∥BC,则∠5=?∠___?(?????????????????????? )
②若AB∥DC,则?∠__=?∠__?(?? ??? ??????)
③∠3=?∠4,则____∥____ (??????????? ????????? )
④若∠D?+?∠DAB?=180°,则____∥____ (???????????????????????????? )
二.平行线性质和判定的进一步应用:
例7:如图,直线a,b被直线c,d所截,,且a∥b,∠1=70°,∠5=50°,这时∠2、∠3、 ∠4各是多少度?为什么?
问1:此题已知量是什么?未知量是什么?它们之间有着怎样的位置关系?
问2:由已知条件“a∥b”可得哪些结论?
解:
∵a∥b(已知),∴∠1=∠2(两直线平行,内错角相等).
∵∠1=70°(已知),∴∠2=70°(等量代换)
∵∠4与∠5是邻补角(已知),∴∠4+∠5=180°(邻补角的意义)∴∠4=180°-∠5=130°
∵a∥b(已知),∴∠3=∠4(两直线平行,同位角相等),∴∠3=130°(等量代换).
〖小结〗在解决问题前,一定要分析待求结论和已知条件之间有什么关系,选择正确的性质定理.
例8:如图:已知AB∥CD,∠1+∠2=180 ,那么CD与EF平行吗?为什么?
问1:要证明两条直线平行有什么方法?
问2:此题中CD与EF平行吗?怎样说明?
答:CD与EF平行.
理由预设1:
∵∠1+∠2=180 (已知),∴AB//EF(同旁内角互补,两直线平行);
又∵AB//CD(已知),∴EF//CD(如果两条直线都与第三条直线平行,那么这两条直线也平行)
预设2:
∵AB ∥CD(已知),∴∠1+∠C=180 (两直线平行,同旁内角互补).
∵∠1+∠2=180 (已知),∴∠2=∠C(同角的补角相等),
∴CD∥EF(同位角相等,两直线平行).
例9 如图,已知∠A=∠D, ∠C=∠F,那么CE与BF平行吗?为什么?
〖分析〗
标记∠A=∠D,∠C=∠F。
问1:∠A与∠D是什么角?由∠A=∠D可得什么结论?
问2:得到FD//AC后,可得∠F(或∠C)与哪个角相等?
答:CE∥BF.
解:∵∠A=∠D(已知),∴AC ∥DF(内错角相等,两直线平行),
方法一:∴∠C=∠DEC(两直线平行,内错角相等)
∵∠C=∠F(已知),∴∠DEC=∠F(等量代换)∴CE∥BF(同位角相等,两直线平行).
方法二:∴∠F=∠FBA(两直线平行,内错角相等).
∵∠C=∠F(已知),∴∠FBA=∠C(等量代换).∴CE∥BF(同位角相等,两直线平行).
三、课堂练习:
A组:
1.填空:如图,
(1)因为∠A=____ (已知),所以AB∥DF( ).
(2)因为∠BDE=_____(已知),所以DF∥AB( ).
(3)因为∠A+∠____=180°(已知),所以AB∥DF( ).
(4)因为∠DFC=∠____ (已知),所以DE∥AC( ).
(5)因为DF∥AB(已知),所以∠B=∠____ ( ).
(6)因为DE∥AC(已知),所以∠BED=∠____ ( ).
2、如图,已知CD∥GF,∠1=∠2,那么DE与BC平行吗?为什么?
B组:
如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以说明.
(1)
四.课堂小结:
1.平行线的性质与判定的联系与区别.
2.平行线性质和判定综合应用中,要抓住“由已知可知什么”、“待求量与已知量之间有何关系”,形成解题思路.
五、布置作业
《练习册》习题13.5(5)
教学目标:
1、通过观察,认识“两直线平行,同位角相等”这一基本事实;初步认识平行线的性质与平行线的判定的区别,并正确选择应用.
2、进一步体会几何说理的过程,学会正确书写证明过程,逐步培养逻辑推理能力,体会化归的数学思想..
教学重点:平行线性质的运用.
教学难点:平行线的性质与平行线的判定的区别.
教学过程:
平行线的性质1
引入:
师:利用同位角相等,可以判定两条直线平行.反过来,如果两条直线平行,同位角相等吗?
演示观察:
教师几何画板演示:(任意两条)平行线a、b被直线l(可动)所截,得同位角、,并测量、的大小.
3、平行线的性质1:
问:通过观察,你能得到什么结论?
平行线的性质1. 两条平行线被第三条直线所截,同位角相等.
简单的说就是:
两直线平行,同位角相等.
如何用符号语言表示这个性质?
(已知)
(两直线平行,同位角相等)
想一想:平行线的判定方法1和平行线的性质1有何区别?
小结:注意平行线的性质和平行线的判定的区别,在应用时正确选用,
若已知两直线平行,由它们的平行得出其他结论,是应用了平行线的性质;
若未知直线平行,而要说明其平行,则需应用平行线的判定.
二、平行线的性质1的应用
例题1 如图,已知直线a、b被直线l所截,a∥b,∠1=50°, 求∠2的度数.
(教师边读题,边在图中标注已知条件.)
问1:题中有哪些已知条件?
问2:已知a∥b,利用平行线的性质,你能得到什么结论?
问3:你说说怎样求出∠2的度数吗?
解:a∥b(已知),∠3=∠2(两直线平行,同位角相等).
∠1与∠3是对顶角,∠1=∠3(对顶角相等).
∠1=∠2(等量代换).
∠1=50°(已知),∠2=50°(等量代换).
小结:
1、题中若给出两直线平行的条件,则要考虑平行线的性质;
2、∠3作为中间量起到了桥梁作用.(类似的,也可找∠2的对顶角解题).
例题2 如图,已知∠B=∠D,AB∥CD,那么DE与BF平行吗?为什么?
问1:你认为DE与BF平行吗?
问2:为什么?
(若学生回答有困难,教师可作如下引导:
问:由已知条件AB∥CD,可以得到什么?
问:要得到DE与BF平行,需要什么条件?
问:怎么可以得到∠1与∠B相等?
解:DE//BF,理由如下:
AB∥CD(已知),∠1=∠D(两直线平行,同位角相等).
∠B=∠D(已知),∠1=∠B(等量代换),
DE∥BF(同位角相等,两直线平行).
小结:解题中正确运用平行线的判定和性质.
例题2的变式训练:已知BF∥DE,AB∥CD,那么∠B=∠D吗?为什么?
三、课堂练习
课本P60,1、2.
A组
1.如图,已知直线、被直线所截,且∥,,求的度数.
解:因为与是对顶角,
所以=_____( ).因为(已知),
得(等量代换).所以(等式性质).
因为∥(已知),得( ).
所以(等量代换).
2.如图,已知∥,如果,那么与相等吗?为什么?
解:因为∥( ),
所以,
( ).
因为( ),
所以________=__________( ).
四、课堂小结:
本节课主要学习了什么?
五、布置作业
练习册13.5 (1)
堂堂练13.5 (1)
13.5平行线的性质(2)
教学目标:
1.探求平行线的性质2、3的过程中,感受化归的数学思想,体会文字语言、图形语言、符号语言之间的互换.
2.在平行线的传递性的推导过程中,感受添加辅助线构造基本图形的策略.
3.通过平行线性质的运用,逐步提高分析能力与简单的逻辑推理能力.
教学重点及难点
重点:平行线性质2、3的运用.
难点:平行线传递性的探求.
教学过程:
一、复习引入
昨天学习了平行线的性质1,如何叙述?
师出示图形,问:如图,如何用符号语言表示?
引言:在学习平行线的判定方法时,我们学会了一种判定方法后,其他判定方法的学习都是通过将新知转化为旧知来解决问题的.现在我们知道了平行线的性质1:两直线平行,同位角相等.则一对内错角的大小之间有什么数量关系?一对同旁内角的大小之间又有什么数量关系呢?
揭示课题:平行线的性质(2)
二、归纳性质
1、如图,直线a、b被直线l所截,a∥b,问∠1与∠2大小有何关系?
师引导:运用学过的性质能否说明你的结论?
说理:a∥b(已知),
∠3=∠2(两直线平行,同位角相等).
又∠1=∠3(对顶角相等),
∠1=∠2(等量代换).
模仿平行线性质1能否说出平行线的性质2?
师补充:简单地说:就是两直线平行,内错角相等.
问:用符号语言如何表示?
2、如图:直线a、b被直线l所截,a∥b,
∠4与∠2这对同旁内角有何数量关系?
问:你能用学过的知识来说明你的结论是正确的吗?
说理:将∠3的邻补角记作∠4,
则∠3+∠4=1800(邻补角的意义)
a∥b(已知)
∠3=∠2(两直线平行,同位角相等)
∠4+∠2=1800(等量代换)
问:还有其他方法吗?
问:你能说出平行线的性质3吗?
问:用符号语言如何表示?
问:平行线的性质与判定有何区别?
教师总结:知道平行用性质;要证平行用判定.
三、实践运用
1、例题3:如图,已知AB∥CD,AD∥BC,那么(1)∠1与∠2相等吗?(2)∠3与∠4呢?
出示第一小问,教师引导方法:观察时只需∠1与∠2,把其他条件隐去.
问1:∠1与∠2是哪两条直线被谁所截得的什么角?
∠1与∠2相等吗?
出示第二小问,让学生分析解答过程.
问2:∠3与∠4哪两条直线被谁所截得的什么角?∠3与∠4相等吗?
【小结】对平行线性质的运用,前提要找到这些角是哪两条直线被哪条直线所截形成的.
2、例题4:如图,已知AB∥CD,AD∥BC,∠A=550,求∠C的度数.
问:根据已知条件,可直接得到哪些角的度数?
求∠C可以怎么思考?
说明:教师边说边勾出∠B或∠D的边进行分析.
解:AD∥BC(已知),
∠A+∠B=1800(两直线平行,同旁内角互补).
∠A=550(已知),
∠B=1800-550=1250(等式性质)
同理可得:∠C=550.
3、思考:如图,有三条直线a,b,c,已知a∥b,b∥c,这时直线a与c有怎样的位置关系?
师引导:要证平行,怎么办?启发学生说出需要同位角,内错角或同旁内角.或者启发学生发现需要三线八角这样的基本图形.
师:现在图形不满足条件,需要构造同位角.我们可以怎么构造?
请学生操作:添一条直线l,分别与a,b,c相交.
师引导分析:要说明a∥c,只要说明什么相等?
如何说理?
得到平行线的传递性:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
简单地说:平行于同一条直线的两条直线平行.
问:如何用符号语言表示?
四、 课堂练习,及时巩固
1、书P62:1、2
A组:
如图,已知直线AB、CD被直线AE所截,且AB∥CD.
(1)从∠1=115°,可以得到∠3是多少度?为什么? (2)从∠1=115°,可以得到∠2是多少度?为什么?
(3)从∠1=115°,可以得到∠4是多少度?为什么?
2.如图,直线DE经过点A,DE∥BC,∠B=42°,∠C=57°,求∠DAB、∠CAD的度数.
B组:
1.指出练习13.4(3)第(3)题中互相垂直的直线.
2、如图:考古学家挖掘出一个梯形残缺玉片,工作人员从玉片上已经量的∠A=1150,∠D=1000.已知梯形的两底AD∥BC,请你求出另外两个角的度数.(∠B=65°,∠ C=700)
五、小结
请同学谈谈自己收获与感想.
补充:化归思想.
六、作业:练习部分:P27:13.5(2)
13.5平行线的性质(3)
教学目标:
1.经历测量两条平行线中一直线上的点到另一直线的距离的操作过程,初步理解两条平行线间的距离的概念,体会从特殊到一般的研究问题方法.
2.通过图形的运动,体会平行线间的距离处处相等的初步应用,感受图形运动的数学思想.
教学重难点:
两条平行线间的距离意义及运用.
教学过程:
一、复习旧知,引入课题
复习:
1、什么是两点之间的距离?
2、什么是点到直线的距离?
3、什么是两条平行线之间的距离?
操作1:任意画两条互相平行的直线和:
(1)请同学们在直线上任意取5个点,
度量一下这5个点到直线的距离.
你能得到什么结论?(学号是单号的操作)
(2)请同学们在直线b上任意取5个点,这5个点到直线的距离都相等吗?(学号是双号的操作)
师:通过同学们动手操作度量,交流度量结果,发现了什么?
二、探究新知,讲授新课
两条平行线间的距离:
两条平行线中,任意一条直线上的所有点到另一条直线的距离都是一个定值,这个定值叫做这两条平行线间的距离.
师:概念的关键词是:
及时反馈 如图,已知AB//CD,AD//BC,交BC于点E,交CD与点F.
线段AE的长度是哪两条平行线间的距离?
如何度量AB、CD间的距离?
追问:还有没有其他的表示方法?
思考:如图:直线,点E、F、G、H是直线上的任意一点,
那么、的面积有什么特征?
追问:为什么高等?
与、的面积相等的三角形还有吗?
变式1:
如果我将上图线段AB沿直线a平移,
分别与点E、G构成的三角形面积还是相等的吗?为什么?
师追问:在上图中还有面积相等的三角形吗?
变式2: 如图:直线,点A、E、F在直线上,点B、C、D在直线b上,BC=EF, 与的面积相等吗?为什么?
师问1:你认为与的面积相等吗?
师问2:为什么?
追问:为什么高相等?
答:与的面积相等.
解:作AH1⊥b,垂足为点H1,
作DH2⊥a,垂足为点H2 ,
由,得AH1 = DH2 (平行线间距离的意义).
设和的面积为S1,S2.
∵S1=BCAH1(三角形面积公式),
S2 =EFDH2,
又∵ BC=EF(已知),
∴S1=S2(等量代换).
即:与的面积相等.
拓展:怎样能在这两条平行线间作出一个三角形,使它的面积是的2倍?
三、课堂练习
书P64:1、2
教师巡视,如发现问题,及时解决及指导.
A组
1.如图,直线,那么与
的面积相等吗?为什么?
2. 如图,已知点E、F分别在长方形ABCD的边AB、CD上,且AF//CE,请分别度量AE与CF之间的距离、AF与CE之间的距离(精确到0.1m)
B组
1. 已知:如图,在中,点D在边BC上,且,试说明
2.如图,已知AB//CD,AD//BC,点E是AD上的任一点,,求.(补充)
C组
已知:如图,直线,写出图中所有面积相等的三角形并说明理由.
四、课堂小结
通过这堂课,你学到了什么?
数学思想和方法:在探究平行线间距离的过程中感受从特殊到一般的归纳方法.
五、布置作业
《练习册》P29-30习题13.5(3)
§13.5平行线的性质(4)
教学目标:
1.准确运用平行线判定与性质解决简单的问题,逐步把握平行线的判定与性质之间的区别和联系.
2.进一步体会逻辑说理的方法,感受正确添加辅助线的方法,提高分析问题、解决问题的能力.
教学重点:运用平行线判定与性质解决简单的问题.
教学难点:平行线判定与性质的应用.
教学过程:
一、复习引入
问1:平行线的判定方法是什么?
问2:平行线的性质呢?
问3:平行线的判定与性质的区别是什么,如何正确选择?
【小结】
条件
结论
平行线的判定
角的关系
两直线平行
平行线的性质
两直线平行
角的关系
下面我们用平行线的判定和性质解决一些问题.
二、初步应用
例题1 如图:已知∠BAE=∠CAE,AE∥DB,试说明∠ABD=∠D的理由.
分析已知条件:
在图形中标∠BAD =∠1,∠CAD =∠2,∠ABE=∠3,
问1:由AD//BE可得哪些与∠E、∠3相关的结论?为什么?
问2:说明∠3=∠E还需要哪些条件?依据是什么?
解:∵AD∥BE(已知),
∴∠E=∠2(两直线平行,同位角相等),
∠1=∠3(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠3=∠E(等量代换).
例题2 如图:已知∠ABC=62°,∠1=∠2,求∠C的度数.
问1:已知条件中的关键条件是什么?可得什么结论?为什么?
问2:这里运用了平行线的判定方法,∠1和
∠2是哪两条直线被那条直线所截得到的内错角?
问3:有了平行线后,再利用平行线的性质可得到哪些与∠C相关的结论?为什么?
问4:现在如何求∠C的度数?
解:∵∠1=∠2 (已知),
∴AB∥CD(内错角相等,两直线平行),
∴∠ABC+∠C=180o(两直线平行,同旁内角互补).
∵∠ABC=62o(已知),
∴∠C=118o(等式性质).
*问5:能求∠A的度数吗?为什么?
三、拓展提高
例题3 如图,已知AB//CD,那么∠B+∠BED+∠D等于多少度?为什么?
j,
问1:你能猜测∠B+∠BED+∠D等于多少度吗?
问2:360°是两个180°的和。什么位置关系的角的数量关系会出现180°?
问3:我们需要有两组平行线构造出两对同旁内角,你会这样去构造出这两组平行线呢?
问4:如果过点E作EF//AB,有什么帮助吗?
问5:∠D+∠DEF如何求?为什么?
解:过点E作EF//AB,得∠B+∠BEF=180o(两直线平行,同旁内角互补).
因为AB//CD(已知),EF//AB(所作),
所以EF//CD(平行线的传递性).得∠D+∠DEF=180o(两平线平行,同旁内角互补).
因此∠B+∠BEF+∠DEF十∠D=360o,即∠B+∠BED+∠D=360o.
四、课堂练习
A组:
如图,已知AB∥CD,∠A=32°,∠B=68°,求∠BEF的度数.
2.如图,已知直线、被直线所截,∥且∠1=∠2=,求∠1、∠2的度数.
B组:如图,已知AB∥CD,,那么∠B、∠BED、∠D有怎样的数量关系?为什么?
五、课堂小结
谈谈这节课你有什么收获、体会或想法?
教师说明:解题过程中理解、体会图形语言、符号语言、数学语言的转化和合理应用.
六、布置作业
《练习册》习题13.5(4)
§13.5平行线的性质(5)
教学目标:
1.综合运用平行线的判定和性质解决问题,培养逻辑思维能力.
2.进一步了解说理的叙述和表达要求,体会几何说理的过程.
教学重点及难点:
平行线的判定和性质的综合运用.
教学过程:
一.复习引入:
师:我们知道由两条直线平行可以得到一些特殊角之间的数量关系,反之,也可以根据一些角度之间的数量关系来判断两条直线平行.
师:若已知两直线平行时,用什么定理?若已知两角之间的关系去判断平行,用什么定理?
思考:填空:如图,
① AD∥BC,则∠5=?∠___?(?????????????????????? )
②若AB∥DC,则?∠__=?∠__?(?? ??? ??????)
③∠3=?∠4,则____∥____ (??????????? ????????? )
④若∠D?+?∠DAB?=180°,则____∥____ (???????????????????????????? )
二.平行线性质和判定的进一步应用:
例7:如图,直线a,b被直线c,d所截,,且a∥b,∠1=70°,∠5=50°,这时∠2、∠3、 ∠4各是多少度?为什么?
问1:此题已知量是什么?未知量是什么?它们之间有着怎样的位置关系?
问2:由已知条件“a∥b”可得哪些结论?
解:
∵a∥b(已知),∴∠1=∠2(两直线平行,内错角相等).
∵∠1=70°(已知),∴∠2=70°(等量代换)
∵∠4与∠5是邻补角(已知),∴∠4+∠5=180°(邻补角的意义)∴∠4=180°-∠5=130°
∵a∥b(已知),∴∠3=∠4(两直线平行,同位角相等),∴∠3=130°(等量代换).
〖小结〗在解决问题前,一定要分析待求结论和已知条件之间有什么关系,选择正确的性质定理.
例8:如图:已知AB∥CD,∠1+∠2=180 ,那么CD与EF平行吗?为什么?
问1:要证明两条直线平行有什么方法?
问2:此题中CD与EF平行吗?怎样说明?
答:CD与EF平行.
理由预设1:
∵∠1+∠2=180 (已知),∴AB//EF(同旁内角互补,两直线平行);
又∵AB//CD(已知),∴EF//CD(如果两条直线都与第三条直线平行,那么这两条直线也平行)
预设2:
∵AB ∥CD(已知),∴∠1+∠C=180 (两直线平行,同旁内角互补).
∵∠1+∠2=180 (已知),∴∠2=∠C(同角的补角相等),
∴CD∥EF(同位角相等,两直线平行).
例9 如图,已知∠A=∠D, ∠C=∠F,那么CE与BF平行吗?为什么?
〖分析〗
标记∠A=∠D,∠C=∠F。
问1:∠A与∠D是什么角?由∠A=∠D可得什么结论?
问2:得到FD//AC后,可得∠F(或∠C)与哪个角相等?
答:CE∥BF.
解:∵∠A=∠D(已知),∴AC ∥DF(内错角相等,两直线平行),
方法一:∴∠C=∠DEC(两直线平行,内错角相等)
∵∠C=∠F(已知),∴∠DEC=∠F(等量代换)∴CE∥BF(同位角相等,两直线平行).
方法二:∴∠F=∠FBA(两直线平行,内错角相等).
∵∠C=∠F(已知),∴∠FBA=∠C(等量代换).∴CE∥BF(同位角相等,两直线平行).
三、课堂练习:
A组:
1.填空:如图,
(1)因为∠A=____ (已知),所以AB∥DF( ).
(2)因为∠BDE=_____(已知),所以DF∥AB( ).
(3)因为∠A+∠____=180°(已知),所以AB∥DF( ).
(4)因为∠DFC=∠____ (已知),所以DE∥AC( ).
(5)因为DF∥AB(已知),所以∠B=∠____ ( ).
(6)因为DE∥AC(已知),所以∠BED=∠____ ( ).
2、如图,已知CD∥GF,∠1=∠2,那么DE与BC平行吗?为什么?
B组:
如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以说明.
(1)
四.课堂小结:
1.平行线的性质与判定的联系与区别.
2.平行线性质和判定综合应用中,要抓住“由已知可知什么”、“待求量与已知量之间有何关系”,形成解题思路.
五、布置作业
《练习册》习题13.5(5)
