陕西省黄陵中学(普通班)2019-2020学年高一上学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 陕西省黄陵中学(普通班)2019-2020学年高一上学期期末考试数学试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 234.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 22:03:26 | ||
图片预览



文档简介
高一普通班期末模拟考试
数学试题
第I卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每个小题所给出的四个选项中,只 有一项是符合题目要求的,把正确选项的代号填在答题卡的指定位置.)
1.已知集合,集合,则
A. B. C. D.
2.设集合,若:是集合到集合的映射,则集合可以是
A. B. C. D.
3.已知角的顶点与平面直角坐标系的原点重合,始边与轴的非负半轴重合,终边经过点,则等于
A. B. C. D.
4.要得到函数的图象,只需将函数图象
A.向右平移的单位 B.向右平移的单位
C.向左平移的单位 D.向左平移的单位
5.下列函数中,在区间上为增函数的是
A. B. C. D.
6.已知是第三象限角,,则
A. B. C. D.
7.函数的零点所在的区间为
A. B. C. D.
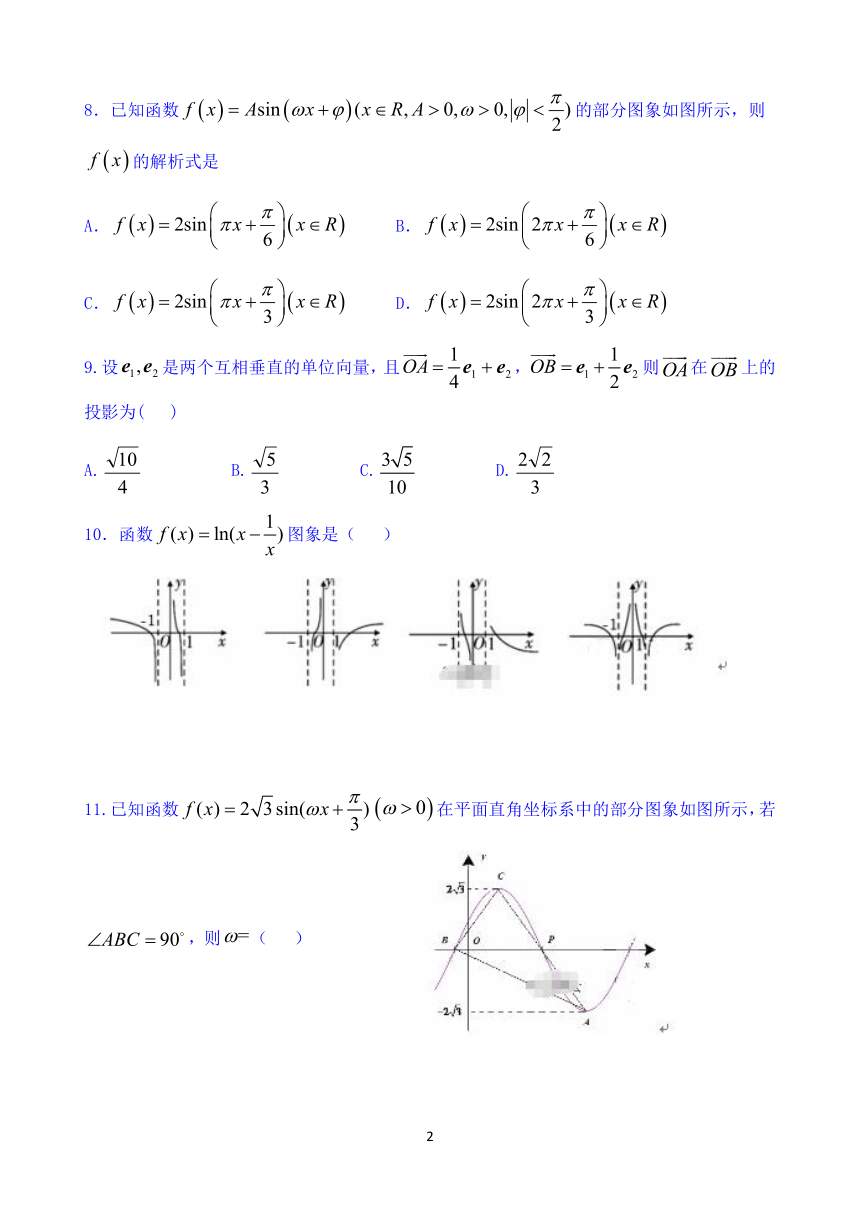
8.已知函数的部分图象如图所示,则的解析式是
A. B.
C. D.
9.设是两个互相垂直的单位向量,且,则在上的投影为( )
A. B. C. D.
10.函数图象是( )
11.已知函数在平面直角坐标系中的部分图象如图所示,若,则( )
A. B. C. D.
12.已知函数,则函数的零点个数为( )
A.1 B.3 C.4 D.6
第Ⅱ卷(非选择题共90分)
二、填空题(本大题共4小题,每小题5分,满分20分)
13.计算: ▲ ; ▲ .
14.已知函数,则 ▲ ;若,则
实数 ▲ .
15.已知函数有三个零点、、,则实数的取值范围
是 ▲ ;的取值范围是 ▲ .
16.已知,则 ▲ .
三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤.)
17.(10分)
(1);
(2).
18.(12分)已知一扇形的中心角是α,所在圆的半径是R.
(1)若α=60°,R=10cm,求扇形的弧长及该弧所在的弓形面积;
(2)若扇形的周长是一定值C(C>0),当α为多少弧度时,该扇形有最大面积?
19.(12分)已知函数
(1)求的单调递增区间
(2)若,已知,求的值
20.(12分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元。
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎样分配资金才能获得最大收益?其最大收益为多少万元?
21(12分).已知.
(1)当时,解不等式;
(2)若,解关于x的不等式.
22.(12分)已知函数为奇函数,且,其中,.
(1)求,的值.
(2)若,,求的值.
数学试题参考答案
D 2.D 3.B 4.A 5.A 6.D 7.A 8.A
9.C 10.B 11.A 12.C
13.; 14.; 15.;
16.
17【答案】(1)0.55(2)1
【解析】(1)利用根式与分数指数幂的性质直接求解.
(2)直接利用对数运算法则及换底公式.
【详解】
(1)
=0.3+2﹣3+2﹣2﹣2﹣3
=0.3+0.25
=0.55.
=1
18【答案】(1)50cm2(2)
【解析】(1)设弧长为l,弓形面积为S弓.
∵α=60°=,R=10,∴l=π(cm).
S弓=S扇-S△=×π×10-×102·sin60°=50cm2.
∵扇形周长C=2R+l=2R+αR,∴R=,∴S扇=α·R2=α=,当且仅当α=,即α=2(α=-2舍去)时,扇形面积有最大值.
19.【答案】(1)
(2)
【解析】(1)由二倍角的正弦、余弦公式可得,再结合正弦函数单调区间的求法即可得解;
(2)由已知可得,,再由辅助角公式运算即可.
【详解】
解:(1)因为,
由,解得:,
故的单调递增区间为:;
(2)由,则,
由,所以,则,
所以,
故.
20.【答案】(1),;(2)债券类产品投资16万元时,收益最大,为3万元
【解析】(1)由题意,得到,,代入求得的值,即可得到函数的解析式;
(2)设债券类产品投资万元,可得股票类产品投资万元,求得总的理财收益的解析式,利用换元法和二次函数的性质,即可求解.
【详解】
(1)设投资债券类产品的收益与投资额的函数关系式为,
投资股票类产品的收益与投资额的函数关系式为,
可知,,
所以,.
(2)设债券类产品投资万元,则股票类产品投资万元,
总的理财收益.
令,则,,
故,
所以,当时,即债券类产品投资16万元时,收益最大,为3万元.
21.【答案】(1)或;(2)答案不唯一,具体见解析
【解析】(1)将代入,解对应的二次不等式可得答案; (2)对值进行分类讨论,可得不同情况下不等式的解集.
【详解】
解:(1)当时,有不等式,
,
∴不等式的解集为或
(2)∵不等式
又
当时,有,∴不等式的解集为;
当时,有,∴不等式的解集为;
当时,不等式的解集为.
22.【答案】(1);(2).
【解析】试题分析:(1)先根据奇函数性质得y2=cos(2x+θ)为奇函数,解得θ= ,再根据解得a(2)根据条件化简得sinα=,根据同角三角函数关系得cosα,最后根据两角和正弦公式求sin的值
试题解析:(1)因为f(x)=(a+2cos2x)cos(2x+θ)是奇函数,而y1=a+2cos2x为偶函数,所以y2=cos(2x+θ)为奇函数,由θ∈(0,π),得θ=,所以f(x)=-sin 2x·(a+2cos2x),
由f=0得-(a+1)=0,即a=-1.
(2)由(1)得f(x)=-sin 4x,因为f=-sin α=-,
即sin α=,又α∈,从而cos α=-,
所以sin=sin αcos+cos αsin=×+×=.
数学试题
第I卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每个小题所给出的四个选项中,只 有一项是符合题目要求的,把正确选项的代号填在答题卡的指定位置.)
1.已知集合,集合,则
A. B. C. D.
2.设集合,若:是集合到集合的映射,则集合可以是
A. B. C. D.
3.已知角的顶点与平面直角坐标系的原点重合,始边与轴的非负半轴重合,终边经过点,则等于
A. B. C. D.
4.要得到函数的图象,只需将函数图象
A.向右平移的单位 B.向右平移的单位
C.向左平移的单位 D.向左平移的单位
5.下列函数中,在区间上为增函数的是
A. B. C. D.
6.已知是第三象限角,,则
A. B. C. D.
7.函数的零点所在的区间为
A. B. C. D.
8.已知函数的部分图象如图所示,则的解析式是
A. B.
C. D.
9.设是两个互相垂直的单位向量,且,则在上的投影为( )
A. B. C. D.
10.函数图象是( )
11.已知函数在平面直角坐标系中的部分图象如图所示,若,则( )
A. B. C. D.
12.已知函数,则函数的零点个数为( )
A.1 B.3 C.4 D.6
第Ⅱ卷(非选择题共90分)
二、填空题(本大题共4小题,每小题5分,满分20分)
13.计算: ▲ ; ▲ .
14.已知函数,则 ▲ ;若,则
实数 ▲ .
15.已知函数有三个零点、、,则实数的取值范围
是 ▲ ;的取值范围是 ▲ .
16.已知,则 ▲ .
三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤.)
17.(10分)
(1);
(2).
18.(12分)已知一扇形的中心角是α,所在圆的半径是R.
(1)若α=60°,R=10cm,求扇形的弧长及该弧所在的弓形面积;
(2)若扇形的周长是一定值C(C>0),当α为多少弧度时,该扇形有最大面积?
19.(12分)已知函数
(1)求的单调递增区间
(2)若,已知,求的值
20.(12分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元。
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎样分配资金才能获得最大收益?其最大收益为多少万元?
21(12分).已知.
(1)当时,解不等式;
(2)若,解关于x的不等式.
22.(12分)已知函数为奇函数,且,其中,.
(1)求,的值.
(2)若,,求的值.
数学试题参考答案
D 2.D 3.B 4.A 5.A 6.D 7.A 8.A
9.C 10.B 11.A 12.C
13.; 14.; 15.;
16.
17【答案】(1)0.55(2)1
【解析】(1)利用根式与分数指数幂的性质直接求解.
(2)直接利用对数运算法则及换底公式.
【详解】
(1)
=0.3+2﹣3+2﹣2﹣2﹣3
=0.3+0.25
=0.55.
=1
18【答案】(1)50cm2(2)
【解析】(1)设弧长为l,弓形面积为S弓.
∵α=60°=,R=10,∴l=π(cm).
S弓=S扇-S△=×π×10-×102·sin60°=50cm2.
∵扇形周长C=2R+l=2R+αR,∴R=,∴S扇=α·R2=α=,当且仅当α=,即α=2(α=-2舍去)时,扇形面积有最大值.
19.【答案】(1)
(2)
【解析】(1)由二倍角的正弦、余弦公式可得,再结合正弦函数单调区间的求法即可得解;
(2)由已知可得,,再由辅助角公式运算即可.
【详解】
解:(1)因为,
由,解得:,
故的单调递增区间为:;
(2)由,则,
由,所以,则,
所以,
故.
20.【答案】(1),;(2)债券类产品投资16万元时,收益最大,为3万元
【解析】(1)由题意,得到,,代入求得的值,即可得到函数的解析式;
(2)设债券类产品投资万元,可得股票类产品投资万元,求得总的理财收益的解析式,利用换元法和二次函数的性质,即可求解.
【详解】
(1)设投资债券类产品的收益与投资额的函数关系式为,
投资股票类产品的收益与投资额的函数关系式为,
可知,,
所以,.
(2)设债券类产品投资万元,则股票类产品投资万元,
总的理财收益.
令,则,,
故,
所以,当时,即债券类产品投资16万元时,收益最大,为3万元.
21.【答案】(1)或;(2)答案不唯一,具体见解析
【解析】(1)将代入,解对应的二次不等式可得答案; (2)对值进行分类讨论,可得不同情况下不等式的解集.
【详解】
解:(1)当时,有不等式,
,
∴不等式的解集为或
(2)∵不等式
又
当时,有,∴不等式的解集为;
当时,有,∴不等式的解集为;
当时,不等式的解集为.
22.【答案】(1);(2).
【解析】试题分析:(1)先根据奇函数性质得y2=cos(2x+θ)为奇函数,解得θ= ,再根据解得a(2)根据条件化简得sinα=,根据同角三角函数关系得cosα,最后根据两角和正弦公式求sin的值
试题解析:(1)因为f(x)=(a+2cos2x)cos(2x+θ)是奇函数,而y1=a+2cos2x为偶函数,所以y2=cos(2x+θ)为奇函数,由θ∈(0,π),得θ=,所以f(x)=-sin 2x·(a+2cos2x),
由f=0得-(a+1)=0,即a=-1.
(2)由(1)得f(x)=-sin 4x,因为f=-sin α=-,
即sin α=,又α∈,从而cos α=-,
所以sin=sin αcos+cos αsin=×+×=.
同课章节目录
