2019-2020学年江西省吉安市四校高二(上)期中数学试卷(文科) word版试卷及答案 解析版
文档属性
| 名称 | 2019-2020学年江西省吉安市四校高二(上)期中数学试卷(文科) word版试卷及答案 解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-06 22:41:32 | ||
图片预览




文档简介
2019-2020学年高二(上)期中数学试卷(文科)
一、选择题(本大题共12小题,每小题5分,共60分)
1.直线l:x+y﹣3=0的倾斜角为( )
A.30° B.60° C.120° D.90°
2.已知直线l:y+m(x+1)=0与直线my﹣(2m+1)x=1平行,则直线l在x轴上的截距是( )
A.1 B. C.﹣1 D.﹣2
3.下列说法正确的是( )
A.命题“?x>0,sinx≤x”的否定是“?x≤0,sinx>x
B.命题“若x≠y,则sinx≠siny”的逆否命题是真命题
C.两平行线2x+2y﹣1=0与2x+2y﹣3=0之间的距离为
D.直线l1:ax+y+1=0,l2:x+ay﹣2=0,l1⊥l2的充要条件是a=±1
4.已知命题p:?x∈R,;命题q:?x0∈R,sinx0>1,则下列命题中为真命题的是( )
A.¬p∧¬q B.p∧¬q C.¬p∧q D.p∧q
5.直线l与圆x2+y2+2x﹣4y+1=0相交于A,B两点,若弦AB的中点(﹣2,3),则直线l的方程为( )
A.x+y﹣3=0 B.x+y﹣1=0 C.x﹣y+5=0 D.x﹣y﹣5=0
6.设m,n是两条不同的直线,α、β、γ是三个不同的平面,给出下列命题:
①若m⊥α,n∥α,则m⊥n;
②若α∥β,β∥γ,m⊥α,则m⊥γ;
③若m∥α,m∥β,则α∥β;
④若α⊥γ,β⊥γ,则α∥β.
其中正确命题的序号是( )
A.①② B.②③ C.③④ D.①④
7.设F1,F2是椭圆+=1(a>b>0)的左右焦点,过点F1,F2作x轴的垂线交椭圆四点构成一个正方形,则椭圆的离心率e为( )
A. B. C. D.
8.某三棱锥的三视图如图所示,则该三棱锥的表面积是( )
A.2+ B.4+ C.2+2 D.5
9.若实数x,y满足,则z=2x+y的最大值为( )
A.3 B.4 C.8 D.9
10.当曲线y=﹣与直线kx﹣y+2k﹣4=0有两个相异的交点时,实数k的取值范围是( )
A.(0,) B.(,] C.(,1] D.(,+∞)
11.直线与圆O:x2+y2=4交于A、B两点,则=( )
A.2 B.﹣2 C.4 D.﹣4
12.已知四棱锥P﹣ABCD的底面为矩形,平面PAD⊥平面ABCD,,PA=PD=AD=3,则四棱锥P﹣ABCD的外接球的表面积为( )
A.20π B.18π C.16π D.12π
二、填空题(每大题共4小题,每小题5分,共20分)
13.等腰梯形ABCD中,上底CD=1,腰,下底AB=3,以下底所在直线为x轴,则由斜二测画法画出的直观图A′B′C′D′的面积为 .
14.一个圆锥的表面积为πa(cm2),且它的侧面展开图是一个半圆,则该圆锥的底面半径为 .
15.已知P:A={x|(x﹣1)(x﹣2)>0},q:B={x|x﹣a≤0},若p是q的必要不充分条件,则实数{x|x﹣a≤0}的取值范围为 .
16.已知过点(2,4)的直线l被圆C:x2+y2﹣2x﹣4y﹣5=0截得的弦长为6,则直线l的方程为 .
三、解答题
17.已知命题p:关于x的方程x2﹣ax+4=0有实根;命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数,若“p或q”是真命题,“p且q”是假命题,求实数a的取值范围.
18.如图,在四棱锥P﹣ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=1,点M是棱PC上的一点,且AM⊥PB.
(Ⅰ)求三棱锥C﹣PBD的体积;
(Ⅱ)证明:AM⊥平面PBD.
19.已知圆C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若,求实数k的值.
20.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥底面ABCD,PD=DC=2,E,F,G分别是AB,PB,CD的中点.
(1)求证:AC⊥PB;
(2)求证:GF∥平面PAD;
(3)求点G到平面PAB的距离.
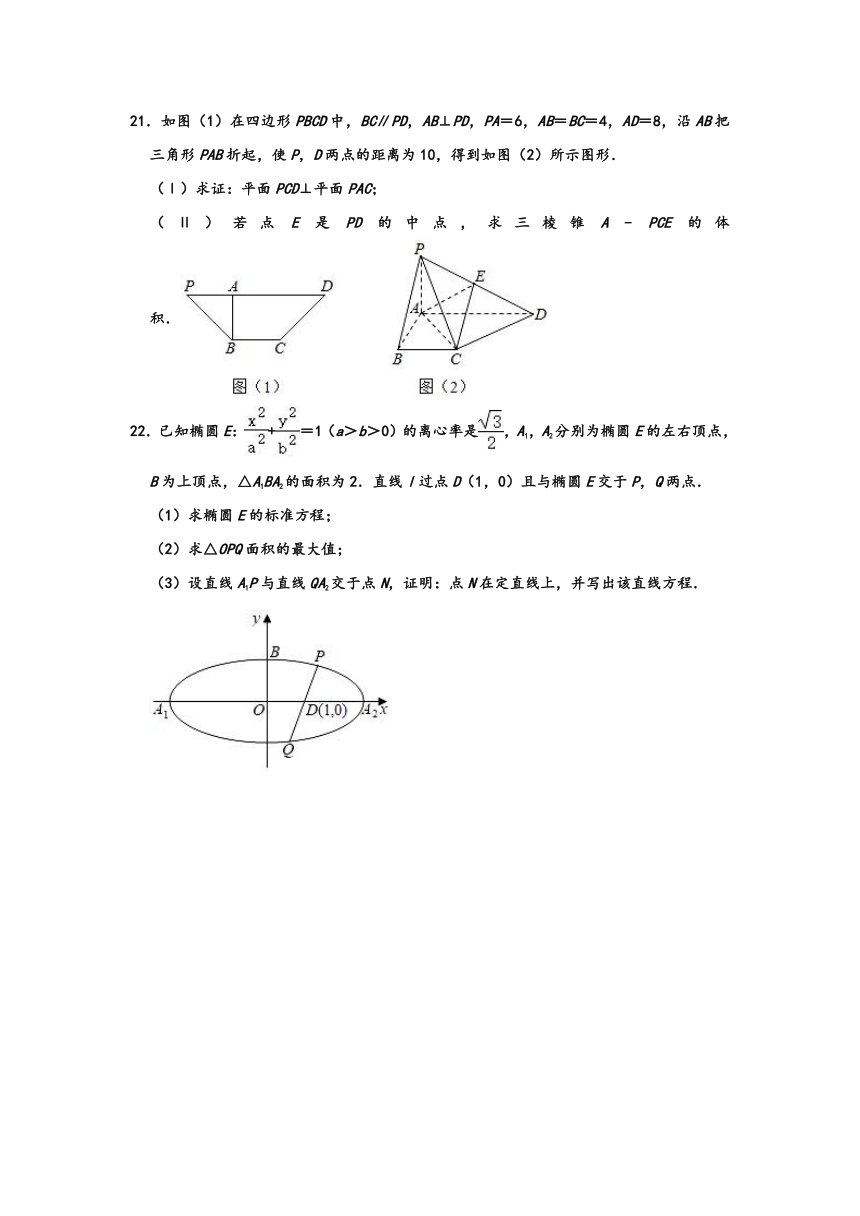
21.如图(1)在四边形PBCD中,BC∥PD,AB⊥PD,PA=6,AB=BC=4,AD=8,沿AB把三角形PAB折起,使P,D两点的距离为10,得到如图(2)所示图形.
(Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅱ)若点E是PD的中点,求三棱锥A﹣PCE的体积.
22.已知椭圆E:+=1(a>b>0)的离心率是,A1,A2分别为椭圆E的左右顶点,B为上顶点,△A1BA2的面积为2.直线l过点D(1,0)且与椭圆E交于P,Q两点.
(1)求椭圆E的标准方程;
(2)求△OPQ面积的最大值;
(3)设直线A1P与直线QA2交于点N,证明:点N在定直线上,并写出该直线方程.
参考答案
一、选择题(本大题共12小题,每小题5分,共60分)
1.直线l:x+y﹣3=0的倾斜角为( )
A.30° B.60° C.120° D.90°
解:直线l:x+y﹣3=0,
可得y=3﹣x,
即有直线的斜率为k=﹣,
设倾斜角为α,
即有tanα=﹣,
由α为钝角,可得α=120°,
故选:C.
2.已知直线l:y+m(x+1)=0与直线my﹣(2m+1)x=1平行,则直线l在x轴上的截距是( )
A.1 B. C.﹣1 D.﹣2
解:化直线的方程为一般式可得
l:mx+y+m=0,(2m+1)x﹣my=1=0,
由直线平行可得(2m+1)=﹣m2,
解得m=﹣1,
经验证当m=﹣1时,满足两直线平行,
∴直线l:y﹣x﹣1=0,
令y=0可得x=﹣1,
∴直线l在x轴上的截距为:﹣1
故选:C.
3.下列说法正确的是( )
A.命题“?x>0,sinx≤x”的否定是“?x≤0,sinx>x
B.命题“若x≠y,则sinx≠siny”的逆否命题是真命题
C.两平行线2x+2y﹣1=0与2x+2y﹣3=0之间的距离为
D.直线l1:ax+y+1=0,l2:x+ay﹣2=0,l1⊥l2的充要条件是a=±1
解:命题“?x>0,sinx≤x”的否定是“?x>0,sinx>x,所以A错误;
命题“若x≠y,则sinx≠siny”为假命题,故其逆否命题为假命题,所以B错误;
两平行线2x+2y﹣1=0与2x+2y﹣3=0之间的距离为:=,所以C正确;
直线l1:ax+y+1=0,l2:x+ay﹣2=0,l1⊥l2的充要条件是a=0,故D不正确;
故选:C.
4.已知命题p:?x∈R,;命题q:?x0∈R,sinx0>1,则下列命题中为真命题的是( )
A.¬p∧¬q B.p∧¬q C.¬p∧q D.p∧q
解:∵x2+2x+3=(x+1)2+2≥2,
∴log2(x2+2x+3)≥log22=1,
即命题p是假命题,
∵?x∈R,﹣1≤sinx≤1,∴命题q是假命题,
则¬p∧¬q是真命题,其余为假命题,
故选:A.
5.直线l与圆x2+y2+2x﹣4y+1=0相交于A,B两点,若弦AB的中点(﹣2,3),则直线l的方程为( )
A.x+y﹣3=0 B.x+y﹣1=0 C.x﹣y+5=0 D.x﹣y﹣5=0
解:圆x2+y2+2x﹣4y+1=0化为标准方程为(x+1)2+(y﹣2)2=4,圆心坐标为C(﹣1,2).
∵弦AB的中点D(﹣2,3),
∴kCD==﹣1,
∴直线l的斜率为1,
∴直线l的方程为y﹣3=x+2,即x﹣y+5=0.
故选:C.
6.设m,n是两条不同的直线,α、β、γ是三个不同的平面,给出下列命题:
①若m⊥α,n∥α,则m⊥n;
②若α∥β,β∥γ,m⊥α,则m⊥γ;
③若m∥α,m∥β,则α∥β;
④若α⊥γ,β⊥γ,则α∥β.
其中正确命题的序号是( )
A.①② B.②③ C.③④ D.①④
解:①若n∥α,经过n的平面与α交于a,根据线面平行的性质定理,可得n∥a,m⊥α,则m⊥a,∴m⊥n,正确;
②若α∥β,β∥γ,则α∥γ,由m⊥α,可得m⊥γ,正确;
③若m∥α,m∥β,则α∥β或α,β相交,故不正确;
④若α⊥γ,β⊥γ,则α∥β或α,β相交,故不正确;
故选:A.
7.设F1,F2是椭圆+=1(a>b>0)的左右焦点,过点F1,F2作x轴的垂线交椭圆四点构成一个正方形,则椭圆的离心率e为( )
A. B. C. D.
解:F1,F2是椭圆+=1(a>b>0)的左右焦点,过点F1,F2作x轴的垂线交椭圆四点构成一个正方形,所以(c,c)是椭圆上的点,可得:,
即,
a2c2﹣c4+a2c2=a4﹣a2c2,
可得e4﹣3e2+1=0.解得e==.
故选:B.
8.某三棱锥的三视图如图所示,则该三棱锥的表面积是( )
A.2+ B.4+ C.2+2 D.5
解:根据三视图可判断直观图为:
OA⊥面ABC,AC=AB,E为BC中点,
EA=2,EC=EB=1,OA=1,
∴可得AE⊥BC,BC⊥OA,
由直线与平面垂直的判定定理得:BC⊥面AEO,AC=,OE=
∴S△ABC=2×2=2,S△OAC=S△OAB=×1=.
S△BCO=2×=.
故该三棱锥的表面积是2,
故选:C.
9.若实数x,y满足,则z=2x+y的最大值为( )
A.3 B.4 C.8 D.9
解:由实数x,y满足,画出可行域如图:
目标函数z=2x+y可化为:y=﹣2x+z,
得到一簇斜率为﹣2,截距为z的平行线,
要求z的最大值,须满足截距最大,
∴当目标函数过点A时截距最大,
又,∴x=2,y=4,
∴点A的坐标为(2,4),
∴z的最大值为:2×2+4=8;
故选:C.
10.当曲线y=﹣与直线kx﹣y+2k﹣4=0有两个相异的交点时,实数k的取值范围是( )
A.(0,) B.(,] C.(,1] D.(,+∞)
解:如图,曲线y=﹣是以O(0,0)为圆心,以2为半径的下半圆,
直线kx﹣y+2k﹣4=0过定点D(﹣2,﹣4),
A(﹣2,0),B(2,0),kBD==1,
设直线kx﹣y+2k﹣4=0与圆相切时,
圆心O(0,0)到直线的距离:
d==2,解得k=,
结合图形得当曲线y=﹣与直线kx﹣y+2k﹣4=0有两个相异的交点时,
实数k的取值范围是(,1].
故选:C.
11.直线与圆O:x2+y2=4交于A、B两点,则=( )
A.2 B.﹣2 C.4 D.﹣4
解:圆O:x2+y2=4的圆心是(0,0),由此知圆心到直线的距离是=<2
所以直线与圆相交
故AB=2=2=r,所以∠AOB=
所以=2×2×cos=2
故选:A.
12.已知四棱锥P﹣ABCD的底面为矩形,平面PAD⊥平面ABCD,,PA=PD=AD=3,则四棱锥P﹣ABCD的外接球的表面积为( )
A.20π B.18π C.16π D.12π
解:由题意,由平面PAD⊥平面ABCD,,PA=PD=AD=3,
∴底面ABCD矩形外接圆半径r=.
四棱锥P﹣ABCD的高为:.
球心与圆心的距离为d,构造直角三角形,
即d2+r2=R2,,
解得:R2=5
∴四棱锥P﹣ABCD的外接球的表面积S=4πR2=20π.
故选:A.
二、填空题(每大题共4小题,每小题5分,共20分)
13.等腰梯形ABCD中,上底CD=1,腰,下底AB=3,以下底所在直线为x轴,则由斜二测画法画出的直观图A′B′C′D′的面积为 .
解:在等腰梯形ABCD中,上底CD=1,腰,下底AB=3,
∴高DE=1,
根据斜二测画法的规则可知,A'B'=AB=3,D'C'=DC=1,O'D'=,
直观图中的高D'F=O'D'sin45°═,
∴直观图A′B′C′D′的面积为,
故答案为:;
14.一个圆锥的表面积为πa(cm2),且它的侧面展开图是一个半圆,则该圆锥的底面半径为 cm .
解:设圆锥的底面半径为r,圆锥的母线为l,
则由πl=2πr,解得l=2r;
又圆锥的表面积为S=πr2+πr?2r=3πr2=πa,
解得r2=,所以r=.
故答案为:cm.
15.已知P:A={x|(x﹣1)(x﹣2)>0},q:B={x|x﹣a≤0},若p是q的必要不充分条件,则实数{x|x﹣a≤0}的取值范围为 (﹣∞,1) .
解:∵P:A={x|(x﹣1)(x﹣2)>0};
∴P:{x|x<1或x>2};
∵q:B={x|x﹣a≤0};
∴q:{x|x≤a};
又∵p是q的必要不充分条件;
∴a<1;
故a的取值范围为:(﹣∞,1).
16.已知过点(2,4)的直线l被圆C:x2+y2﹣2x﹣4y﹣5=0截得的弦长为6,则直线l的方程为 x﹣2=0或3x﹣4y+10=0 .
解:设过点(2,4)的直线l的方程为y=k(x﹣2)+4,
圆C:x2+y2﹣2x﹣4y﹣5=0的圆心C(1,2),半径r==,
圆心C(1,2)到直线l的距离d==,
∵过点(2,4)的直线l被圆C:x2+y2﹣2x﹣4y﹣5=0截得的弦长为6,
∴由勾股定理得:,即,
解得k=,∴直线l的方程为y=(x﹣2)+4,即3x﹣4y+10=0,
当直线l的斜率不存在时,直线l的方程为x=2,
圆心C(1,2)到直线x=2的距离d=1,
满足,故x﹣2=0是直线l的方程.
综上,直线l的方程为x﹣2=0或3x﹣4y+10=0.
故答案为:x﹣2=0或3x﹣4y+10=0.
三、解答题
17.已知命题p:关于x的方程x2﹣ax+4=0有实根;命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数,若“p或q”是真命题,“p且q”是假命题,求实数a的取值范围.
解:若p真:则△=a2﹣4×4≥0
∴a≤﹣4或a≥4
若q真:,
∴a≥﹣12
由“p或q”是真命题,“p且q”是假命题得:p、q两命题一真一假
当p真q假时:a<﹣12;当p假q真时:﹣4<a<4
综上,a的取值范围为(﹣∞,﹣12)∪(﹣4,4)
18.如图,在四棱锥P﹣ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=1,点M是棱PC上的一点,且AM⊥PB.
(Ⅰ)求三棱锥C﹣PBD的体积;
(Ⅱ)证明:AM⊥平面PBD.
解:(Ⅰ)PA⊥底面ABCD,PA=1,即三棱锥P﹣BCD的高为PA=1,,…2分
所以,三棱锥C﹣PBD的体积VC﹣PBD=VP﹣BCD,…4分
=AP?S△BCD=…6分
(Ⅱ)由于PA⊥底面ABCD,所以PA⊥BD,…7分
设AC,BD的交点为O,
由正方形知,BD⊥AC,…8分
所以,BD⊥平面PAC,…9分
从而,BD⊥AM…10分
又AM⊥PB,所以,AM⊥平面PBD…12分
19.已知圆C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若,求实数k的值.
解:(I)设圆C(a,a)半径r.因为圆经过A(﹣2,0),B(0,2)
所以:|AC|=|BC|=r,解得a=0,r=2,
所以C的方程x2+y2=4.
(II)方法一:
因为,,
所以,,∠POQ=120°,
所以圆心到直l:kx﹣y+1=0的距离d=1,,所以 k=0.
方法二:P(x1,y1),Q(x2,y2),因,代入消元(1+k2)x2+2kx﹣3=0.
由题意得△=4k2﹣4(1+k2)(﹣3)>0且和
因为,
又y1?y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1,
所以,
化简得:﹣5k2﹣3+3(k2+1)=0,
所以:k2=0即k=0.
20.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥底面ABCD,PD=DC=2,E,F,G分别是AB,PB,CD的中点.
(1)求证:AC⊥PB;
(2)求证:GF∥平面PAD;
(3)求点G到平面PAB的距离.
【解答】(1)证明:如图,连接AC,BD,
因为PD⊥面ABCD,且AC?平面ABCD,
所以AC⊥PD,
又因为四边形ABCD为菱形,
所以AC⊥BD,
又PD∩BD=D,PD,BD?平面PBD,
所以AC⊥平面PBD,
又PB?平面PBD,
所以AC⊥PB;
(2)证明:如图取PA中点H,连接FH,HD,
因为F为PB中点,
所以HF∥AB,且HF=AB,
又因为四边形ABCD为菱形,且G为CD中点,
所以DG∥AB,且DG=AB,
所以HF∥DG,且HF=DG,
所以四边形HDGF为平行四边形,
所以GF∥HD,
因为GF?平面PAD,HD?平面PAD,
所以GF∥平面PAD,
(3)解:设G到平面PAB的距离为h,
因为DC∥AB,DC?平面PAB,AB?平面PAB,
所以DC∥平面PAB,
所以VG﹣PAB=VD﹣PAB=VP﹣ABD,
所以=,
所以h=,
所以G到平面PAB的距离为.
21.如图(1)在四边形PBCD中,BC∥PD,AB⊥PD,PA=6,AB=BC=4,AD=8,沿AB把三角形PAB折起,使P,D两点的距离为10,得到如图(2)所示图形.
(Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅱ)若点E是PD的中点,求三棱锥A﹣PCE的体积.
【解答】证明:(Ⅰ)由已知在图(2)中,PA=6,AD=8,PD=10,
∴PA2+AD2=PD2,∴PA⊥AD,
∵PA⊥AB,∴PA⊥平面ABCD,
∴PA⊥CD,
∵AB=BC=4,AD=8,
∴由平面几何知识得AC=CD=4,
∴AC2+CD2=AD2,∴AC⊥CD,
∵PA∩AC=A,∴CD⊥平面PAC,
∵CD?平面PCD,∴平面PCD⊥平面PAC.
解:(Ⅱ)由(Ⅰ)知PA⊥平面ABCD,
∴平面PAD⊥平面ABCD,
∵AB⊥AD,且平面PAD与平面ABCD的交线为AD,
∴AB⊥平面PAD,
又∵BC∥AD,∴BC∥平面PAD,
∴三棱锥A﹣PCE的体积:
VA﹣PCE=VC﹣PAE=VC﹣PAE=×4=16.
22.已知椭圆E:+=1(a>b>0)的离心率是,A1,A2分别为椭圆E的左右顶点,B为上顶点,△A1BA2的面积为2.直线l过点D(1,0)且与椭圆E交于P,Q两点.
(1)求椭圆E的标准方程;
(2)求△OPQ面积的最大值;
(3)设直线A1P与直线QA2交于点N,证明:点N在定直线上,并写出该直线方程.
解:由题意知e===,
∴=,即a=2b,
∵△A1BA2的面积为2,
∴ab=2,
解得a=2,b=1,
∴椭圆C的标准方程为+y2=1,
(2)PQ斜率不存在时,易知P(1,),Q(1,﹣),此时S△OPQ=,
当直线PQ的斜率存在时,设PQ的方程为y=k(x﹣1),k≠0,
设P(x1,y1),Q(x2,y2),
将y=k(x﹣1)代入+y2=1,整理可得(1+4k2)x2﹣8k2x+4k2﹣4=0,
∴x1+x2=,x1x2=,
∴|x1﹣x2|==,
∴S△OPQ=×1×|y1﹣y2|=?|x1﹣x2|=,
令1+4k2=t,t>1,
∴S△OPQ==<,
故△OPQ面积的最大值
证明(3)PQ斜率不存在时,易知N(4,),
当直线PQ的斜率存在时,直线A1P的方程为y=(x+2),直线A2Q的方程为y=(x﹣2),
∴(x+2)=(x﹣2),
∴=====,
解得x=4,即N点的横坐标为4,
综上所述,点N在定直线x=4上.
同课章节目录
