2019-2020学年上学期高二数学寒假自主先学3 正余弦定理的运用 学生版(Word版)
文档属性
| 名称 | 2019-2020学年上学期高二数学寒假自主先学3 正余弦定理的运用 学生版(Word版) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-07 00:00:00 | ||
图片预览




文档简介
SHAPE \* MERGEFORMAT
1.掌握实际问题中测量距离等问题(重点).
2.掌握实际问题中测量角度的问题(难点).
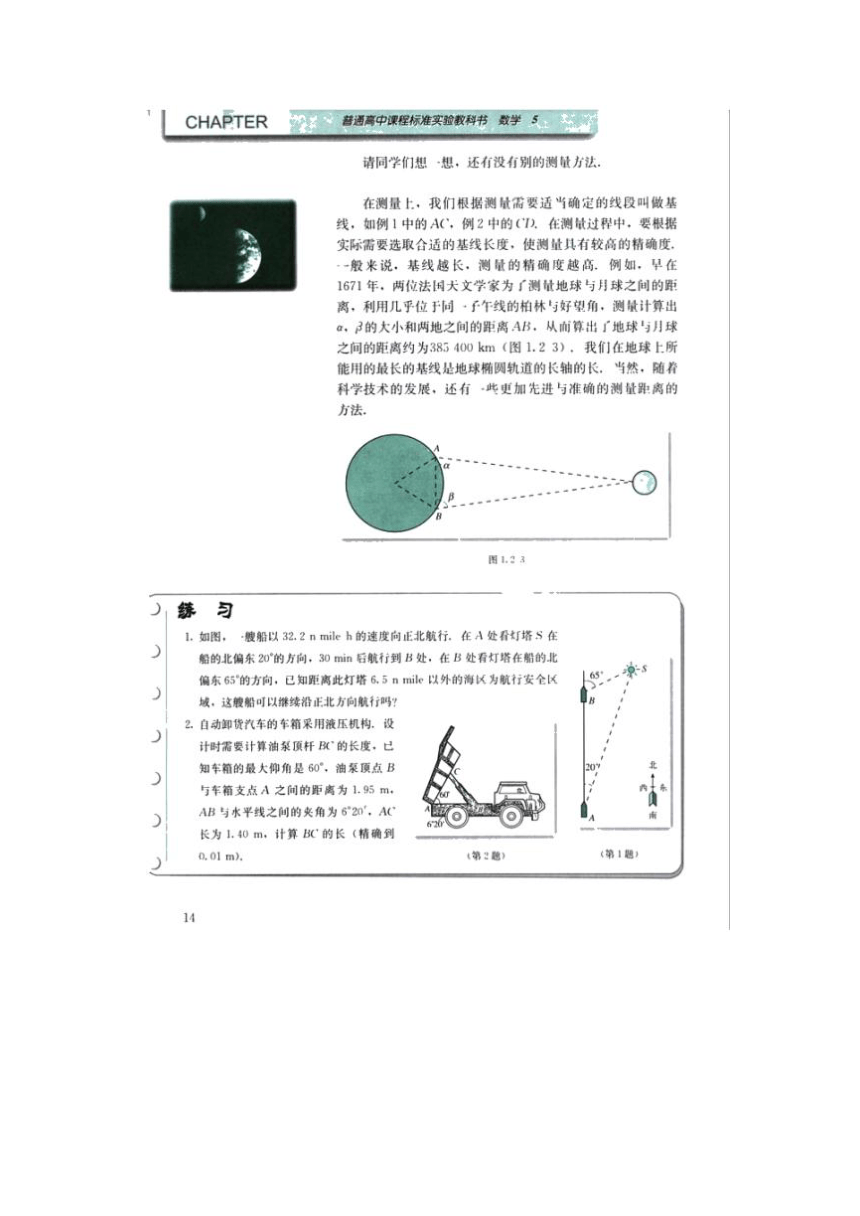
图片:教材截图
知识点1:三角形的面积公式
三角形的面积公式:
.
其中为内切圆半径,为外接圆半径,.
知识点2:测量距离
在观察实验和日常生活以及建筑设计中,少不了遇到测量距离的问题,如测量两河岸之间的距离,测量海上两个岛屿之间的距离等,这些问题的解决都可利用正弦、余弦定理解三角形来实现.同时借助正弦、余弦定理还可以进一步解决一些有关三角形的计算问题.
知识点3:测量高度
利用正弦定理,余弦定理可以解决底(顶)部不能到达的物体的高度问题,常利用解一个直角三角形和一个斜三角形或两个直角三角形使问题得解.解决高度测量问题时,常会遇到仰角、俯角或视角等术语,应正确理解这些概念.
知识点4:测量角度
对于有些与角度有关的实际问题,我们无法直接测量其角度,则需要在实际问题中构造相关三角形,通过三角形,求出相关的角度.
1.在中,三边与面积的关系式为,则角为( )
A. B. C. D.
2.如图,设两点在河的两岸,一测量者在所在的同侧河岸边选定一点,测出的距离为,,后,就可以计算出两点的距离为( )
A. B. C. D.
1.在某次军事演习中红方为了准确分析战场形势,在两个相距为的军事基地和测得蓝方两支精锐部队分别在处和处,且,,,,如图,求蓝方这两支精锐部队的距离.
【答案】
【解析】方法一:∵,
又,∴,∴.
在中,,
由正弦定理得,
.
在中,由余弦定理得
,
∴,∴蓝方这两支精锐部队的距离为.
方法二(同方法一),
在中,,∴,∴.
在中,由余弦定理得
,
∴,∴蓝方这两支精锐部队的距离为.
2.如图,在某点处测得建筑物的顶端的仰角为,沿方向前进,到点处测得顶端的仰角为,再继续前进至点,测得顶端的仰角为,求的大小和建筑物的高.
【答案】
【解析】在已知图形中,角、边关系明显,可用正弦定理.
由于,,成倍角关系,可考虑三角恒等变形的倍角公式.
∵,,∴,∴.
同理,.
在中,,
即,即,.
∴,∴,.
在中,,
即所求角为,建筑物高度为.
1.如图,为了测量两山顶间的距离,飞机沿水平方向在,两点进行测量,,,,在同一个铅垂平面内.飞机能够测量的数据有俯角和,间的距离.请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算,间的距离的步骤.
1.如图所示,为了测量障碍物两侧间的距离,给定下列四组数据,测量时应当选用数据( )
A. B. C. D.
2.如图所示,已知两座灯塔和与海洋观察站的距离都等于,灯塔在观察站的北偏东,灯塔在观察站的南偏东,则灯塔与灯塔的距离为( )
A. B. C. D.
3.在中,,,,则的面积为( )
A. B. C. D.
4.一艘船向正北方向航行,看见正西方向有相距的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西方向,另一灯塔在船的南偏西方向,则这只船的速度是( )
A. B. C. D.
5.据新华社报道,强台风“珍珠”在广东饶平登陆,台风中心最大风力达到级以上,大风、阵雨给灾区带来严重的灾害,不少大树被大风折断.某路边一树干被台风吹断后,折成与地面成的角,树干也倾斜为与地面成的角,树干底部与树尖着地处相距,则折断点与树干底部的距离是( )
A. B. C. D.
6.如图,从气球处测得济南全运会东荷、西柳两个场馆,的俯角分别为,,此时气球的高度为,则两个场馆,间的距离为( )
A. B. C. D.
7.如图,一艘船上午在处测得灯塔在它的北偏东处,之后它继续沿正北方向匀速航行,上午到达处,此时又测得灯塔在它的北偏东处,且与它相距.此船的航速是 .
8.在中,,,是边上的一点,,的面积为,则的长为 .
9.如图,某测量人员为了测量西江北岸不能到达的两点之间的距离,她在西江南岸找到一点,从点可以观察到点;找到一个点,从点可以观察到点,;找到一个点,从点可以观察到点,;并测量得到数据:
,,,,,.
(1)求的面积;
(2)求之间的距离.
10.某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为,,测得,,,.
(1)求的长度;
(2)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计建造费用较低?请说明理由.
即学即练:
1.【答案】A
【解析】因为且,
所以,所以,所以,所以.
2.【答案】A
【解析】由正弦定理得,
又,
∴.
技能应用:
1.【答案】见解析
【解析】方案一:
①需要测量的数据有:点到点,的俯角,;
点到点,的俯角,;,间的距离(如图所示).
②第一步:计算,由正弦定理得;
第二步:计算,由正弦定理得;
第三步:计算,由余弦定理得.
方案二:
①需要测量的数据有:点到点,的俯角,;
点到点,的俯角,;,间的距离(如图所示).
②第一步:计算,由正弦定理得;
第二步:计算,由正弦定理得;
第三步:计算,由余弦定理得.
先学检测:
1.【答案】C
【解析】角不可测量,故排除A,B,D,根据C中数据可用余弦定理求解.
2.【答案】B
【解析】易知,
在中,由余弦定理得
,∴.
3.【答案】C
【解析】∵,,∴,
∴.
4.【答案】C
【解析】如图所示,依题意有,,
所以,从而,
在直角三角形中,可得,于是这只船的速度是.
5.【答案】A
【解析】如图所示,设树干底部为,树尖着地处为,折断点为,
则,,∴,
由正弦定理知,,∴.
6.【答案】B
【解析】在中,,
在中,由正弦定理,得.
7.【答案】
【解析】设船的航速为,
在中,,,,
由正弦定理得,∴.
∴此船的航速为.
8.【答案】或
【解析】如图,设,由,得,
∴.
在中,由余弦定理,,
解得或.
当时,由,得;
又由,得,
当时,同理得.
9.【答案】(1);(2).
【解析】(1)在中,,
.
(2)连接,依题意知,在中,
.
在中,,
由正弦定理,
得,
又
,
在中,由余弦定理,
可得
.
∴.
10.【答案】(1);(2)小李的设计建造费用较低.
【解析】(1)在中,由余弦定理得
,①
在中,由余弦定理及整理得
,②
由①②得,
解得.
又为三角形的内角,即,所以,
又,,所以是等边三角形,故.
(2)小李的设计建造费用较低.
理由如下:,,
因为,,所以,
由题知建造标志费用与用地面积成正比,
故选择建造环境标志费用较低,即小李的设计建造费用较低.
先学目标
先学过程
先学检测
