2020年沪科新版八年级上册数学第12章一次函数单元测试卷(解析版)
文档属性
| 名称 | 2020年沪科新版八年级上册数学第12章一次函数单元测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 316.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-07 00:00:00 | ||
图片预览




文档简介
2020年沪科新版八年级上册数学《第12章 一次函数》单元测试卷
一.选择题(共10小题)
1.以固定的速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球的运动的时间t(秒)之间的关系式是h=v0t﹣4.9t2,在这个关系式中,常量、变量分别为( )
A.4.9是常量,t、h是变量
B.v0是常量,t、h是变量
C.v0、﹣4.9是常量,t、h是变量
D.4.9是常量,v0、t、h是变量
2.下列各曲线表示的y与x的关系中,y不是x的函数的是( )
A. B.
C. D.
3.某商场自行车存放处每周的存车量为5000辆次,其中变速车存车费是每辆一次1元,普通车存车费为每辆一次0.5元,若普通车存车量为x辆次,存车的总收入为y元,则y与x之间的关系式是( )
A.y=0.5x+5000 B.y=0.5x+2500
C.y=﹣0.5x+5000 D.y=﹣0.5x+2500
4.函数y=的自变量x的取值范围是( )
A.x>2 B.x≥2 C.x≠2 D.x≤2
5.若函数,则当自变量x取1,2,3,…,100这100个自然数时,函数值的和是( )
A.540 B.390 C.194 D.197
6.若函数y=(m﹣1)x|m|﹣5是一次函数,则m的值为( )
A.±1 B.﹣1 C.1 D.2
7.若y=(m﹣2)x+(m2﹣4)是正比例函数,则m的取值是( )
A.2 B.﹣2 C.±2 D.任意实数
8.正比例函数y=kx(k≠0)函数值y随x的增大而增大,则y=kx﹣k的图象大致是( )
A. B.
C. D.
9.如图,在同一平面直角坐标系中,表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且mn≠0)图象的是( )
A. B.
C. D.
10.关于一次函数y=﹣2x+3,下列结论正确的是( )
A.图象过点(1,﹣1) B.图象经过一、二、三象限
C.y随x的增大而增大 D.当x>时,y<0
二.填空题(共8小题)
11.在圆的周长公式C=2πr中,变量是 , ,常量是 .
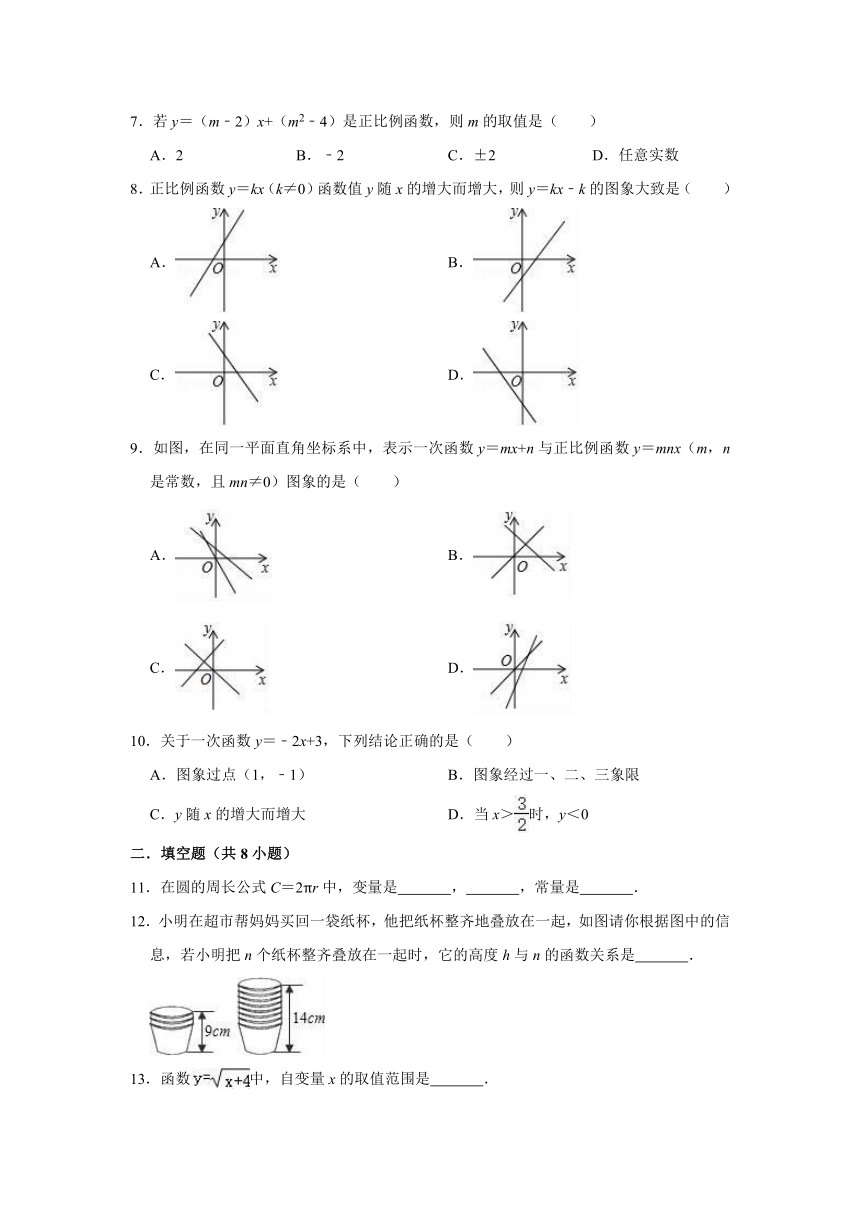
12.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系是 .
13.函数中,自变量x的取值范围是 .
14.函数y=,则当函数值x=﹣1时,y= .
15.已知函数y=(m﹣2)x|m﹣1|+2是关于x的一次函数,则m=
16.当m= 时,函数y=(2m﹣1)x3m﹣2是正比例函数.
17.若函数y=kx+b(k,b为常数)的图象如下图所示,那么当y>0时,x的取值范围是 .
18.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为 .
三.解答题(共8小题)
19.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
20.已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x … 1 2 3 5 7 9 …
y … 1.98 3.95 2.63 1.58 1.13 0.88 …
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为 ;
②该函数的一条性质: .
21.父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
距离地面高度(千米)h 0 1 2 3 4 5
温度(℃)t 20 14 8 2 ﹣4 ﹣10
根据表中,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)表中自变量是 ;因变量是 ;当地面上(即h=0时)时,温度是 ℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足h与t关系的式子.
(3)计算出距离地面6千米的高空温度是多少?
22.物体自由下落的高度h(米)和下落时间t(秒)的关系是:在地球上大约是h=4.9t2,在月球上大约是h=0.8t2,当h=20米时,
(1)物体在地球上和在月球上自由下落的时间各是多少?
(2)物体在哪里下落得快?
23.已知y=(m+1)x2﹣|m|+n+4
(1)当m、n取何值时,y是x的一次函数?
(2)当m、n取何值时,y是x的正比例函数?
24.已知函数y=(m+1)x2﹣|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
25.在同一坐标系中,画出函数y=﹣2x与y=x+1的图象.
26.先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
(1)正比例函数y=2x过( 0, )和( 1, )
(2)一次函数y=﹣x+3过( 0, )和( ,0 )
2020年沪科新版八年级上册数学《第12章 一次函数》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.以固定的速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球的运动的时间t(秒)之间的关系式是h=v0t﹣4.9t2,在这个关系式中,常量、变量分别为( )
A.4.9是常量,t、h是变量
B.v0是常量,t、h是变量
C.v0、﹣4.9是常量,t、h是变量
D.4.9是常量,v0、t、h是变量
【分析】根据在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量,即可答题.
【解答】解:h=v0t﹣4.9t2中的v0(米/秒)是固定的速度,﹣4.9是定值,
故v0和﹣4.9是常量,t、h是变量,
故选:C.
【点评】本题考查了常量与变量的知识,属于基础题,变量是指在程序的运行过程中随时可以发生变化的量.
2.下列各曲线表示的y与x的关系中,y不是x的函数的是( )
A. B.
C. D.
【分析】根据函数的意义即可求出答案.函数的意义反映在图象上简单的判断方法是:做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点.
【解答】解:根据函数的意义可知:对于自变量x的任何值,y都有唯一的值与之相对应,所以只有选项C不满足条件.
故选:C.
【点评】本题主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
3.某商场自行车存放处每周的存车量为5000辆次,其中变速车存车费是每辆一次1元,普通车存车费为每辆一次0.5元,若普通车存车量为x辆次,存车的总收入为y元,则y与x之间的关系式是( )
A.y=0.5x+5000 B.y=0.5x+2500
C.y=﹣0.5x+5000 D.y=﹣0.5x+2500
【分析】根据题意可以写出题目中的函数解关系式,从而可以解答本题.
【解答】解:由题意可得,
y=0.5x+(5000﹣x)×1=﹣0.5x+5000,
故选:C.
【点评】本题考查函数关系式,解答本题的关键是明确题意,写出题目中的函数关系式.
4.函数y=的自变量x的取值范围是( )
A.x>2 B.x≥2 C.x≠2 D.x≤2
【分析】根据被开方数为非负数列出不等式,解之可得.
【解答】解:根据题意知x﹣2≥0,
解得:x≥2,
故选:B.
【点评】本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.
5.若函数,则当自变量x取1,2,3,…,100这100个自然数时,函数值的和是( )
A.540 B.390 C.194 D.197
【分析】将x2﹣100x+196分解为:(x﹣2)(x﹣98),然后可得当2≤x≤98时函数值为0,再分别求出x=1,99,100时的函数值即可.
【解答】解:∵x2﹣100x+196=(x﹣2)(x﹣98)
∴当2≤x≤98时,|x2﹣100x+196|=﹣(x2﹣100x+196),
当自变量x取2到98时函数值为0,
而当x取1,99,100时,|x2﹣100x+196|=x2﹣100x+196,
所以,所求和为(1﹣2)(1﹣98)+(99﹣2)(99﹣98)+(100﹣2)(100﹣98)=97+97+196=390.
故选:B.
【点评】本题考查函数值的知识,有一定难度,关键是将x2﹣100x+196分解为:(x﹣2)(x﹣98)进行解答.
6.若函数y=(m﹣1)x|m|﹣5是一次函数,则m的值为( )
A.±1 B.﹣1 C.1 D.2
【分析】根据一次函数的定义列式计算即可得解.
【解答】解:根据题意得,|m|=1且m﹣1≠0,
解得m=±1且m≠1,
所以,m=﹣1.
故选:B.
【点评】本题主要考查了一次函数的定义,一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.
7.若y=(m﹣2)x+(m2﹣4)是正比例函数,则m的取值是( )
A.2 B.﹣2 C.±2 D.任意实数
【分析】正比例函数的一般式y=kx,k≠0,所以使m2﹣4=0,m﹣2≠0即可得解.
【解答】解:根据题意得:;
得:m=﹣2.
故选:B.
【点评】考查了正比例函数的定义,比较简单.
8.正比例函数y=kx(k≠0)函数值y随x的增大而增大,则y=kx﹣k的图象大致是( )
A. B.
C. D.
【分析】直接利用正比例函数的性质得出k的取值范围,进而得出一次函数经过的象限.
【解答】解:∵正比例函数y=kx(k≠0)函数值y随x的增大而增大,
∴k>0,
∴y=kx﹣k的图象经过第一、三、四象限,
故选:B.
【点评】此题主要考查了一次函数与正比例函数的图象,正确得出k的符号是解题关键.
9.如图,在同一平面直角坐标系中,表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且mn≠0)图象的是( )
A. B.
C. D.
【分析】根据“两数相乘,同号得正,异号得负”分两种情况讨论mn的符号,然后根据m、n同正时,同负时,一正一负或一负一正时,利用一次函数的性质进行判断.
【解答】解:①当mn>0,m,n同号,同正时y=mx+n过第一,二,三象限,同负时过二,三,四象限;
②当mn<0时,m,n异号,则y=mx+n过一,三,四象限或一,二,四象限.
y=mnx过原点,二、四象限.由题意m,n是常数,且mn<0.
故选:A.
【点评】此题主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.
一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
10.关于一次函数y=﹣2x+3,下列结论正确的是( )
A.图象过点(1,﹣1) B.图象经过一、二、三象限
C.y随x的增大而增大 D.当x>时,y<0
【分析】A、把点的坐标代入关系式,检验是否成立;
B、根据系数的性质判断,或画出草图判断;
C、根据一次项系数判断;
D、可根据函数图象判断,亦可解不等式求解.
【解答】解:A、当x=1时,y=1.所以图象不过(1,﹣1),故错误;
B、∵﹣2<0,3>0,
∴图象过一、二、四象限,故错误;
C、∵﹣2<0,
∴y随x的增大而减小,故错误;
D、画出草图.
∵当x>时,图象在x轴下方,
∴y<0,故正确.
故选:D.
【点评】本题主要考查了一次函数的性质以及一次函数与方程、不等式的关系.常采用数形结合的方法求解.
二.填空题(共8小题)
11.在圆的周长公式C=2πr中,变量是 C , r ,常量是 2π .
【分析】根据函数的意义可知:变量是改变的量,常量是不变的量,据此即可确定变量与常量.
【解答】解:∵在圆的周长公式C=2πr中,C与r是改变的,π是不变的;
∴变量是C,r,常量是2π.
【点评】主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
12.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系是 h=n+6 .
【分析】根据等量关系,可得方程组,根据解方程组,可得纸杯的高,纸杯边沿的高,根据纸杯的高加纸杯边沿的高,可得答案.
【解答】解:设纸杯的高是x,纸杯边沿的高是y,由题意,得
,
解得.
高度h与n的函数关系是 h=(n﹣1)+7,
即h=n+6,
故答案为:h=n+6.
【点评】本题考查了函数关系式,利用方程组得出纸杯的高、纸杯边沿的高是解题关键.
13.函数中,自变量x的取值范围是 x≥﹣4 .
【分析】根据二次根式的性质,被开方数大于等于0,就可以求解.
【解答】解:根据题意得:x+4≥0,
解得:x≥﹣4.
故答案为:x≥﹣4.
【点评】本题考查的是函数自变量取值范围的求法.函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数为非负数.
14.函数y=,则当函数值x=﹣1时,y= 6 .
【分析】把x=﹣1代入第一个关系式进行计算即可得解.
【解答】解:x=﹣1时,
y=2x2+4
=2×(﹣1)2+4
=2+4
=6.
故答案为:6.
【点评】本题考查了函数值求解,是基础题,根据x的取值范围确定出函数关系式是解题的关键.
15.已知函数y=(m﹣2)x|m﹣1|+2是关于x的一次函数,则m= 0
【分析】根据一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1,即可得出m的值.
【解答】解:根据一次函数的定义可得:m﹣2≠0,|m﹣1|=1,
由|m﹣1|=1,解得:m=0或2,
又m﹣2≠0,m≠2,
∴m=0.
故答案为:0.
【点评】本题主要考查了一次函数的定义,难度不大,注意基础概念的掌握.
16.当m= 1 时,函数y=(2m﹣1)x3m﹣2是正比例函数.
【分析】直接利用正比例函数的定义得出3m﹣2=1,进而得出答案.
【解答】解:∵函数y=(2m﹣1)x3m﹣2是正比例函数,
∴3m﹣2=1,
解得:m=1.
故答案为:1.
【点评】此题主要考查了正比例函数的定义,正确把握定义是解题关键.
17.若函数y=kx+b(k,b为常数)的图象如下图所示,那么当y>0时,x的取值范围是 x<2 .
【分析】根据一次函数图象的性质利用数形结合可直接解答.
【解答】解:∵由一次函数的图象可知,当x<2时函数的图象在x轴的上方,
∴当y>0时,x的取值范围是x<2.
故答案为:x<2.
【点评】本题考查的是一次函数的图象,利用数形结合求出x的取值范围是解答此题的关键.
18.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为 a<c<b .
【分析】根据直线所过象限可得a<0,b>0,c>0,再根据直线陡的情况可判断出b>c,进而得到答案.
【解答】解:根据三个函数图象所在象限可得a<0,b>0,c>0,
再根据直线越陡,|k|越大,则b>c.
则b>c>a,
故答案为:a<c<b.
【点评】此题主要考查了正比例函数图象,关键是掌握:当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.同时注意直线越陡,则|k|越大
三.解答题(共8小题)
19.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
【分析】根据总价=单价×数量,可得函数关系式.
【解答】解:由题意得:
y=2x,
常量是2,变量是x、y,
x是自变量,y是x的函数.
【点评】主要考查了常量与变量.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
20.已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x … 1 2 3 5 7 9 …
y … 1.98 3.95 2.63 1.58 1.13 0.88 …
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为 2 ;
②该函数的一条性质: 该函数有最大值 .
【分析】(1)按照自变量由小到大,利用平滑的曲线连结各点即可;
(2)①在所画的函数图象上找出自变量为4所对应的函数值即可;
②利用函数图象有最高点求解.
【解答】解:(1)如图,
(2)①x=4对应的函数值y约为2.0;
②该函数有最大值.
故答案为2,该函数有最大值.
【点评】本题考查了函数的定义:对于函数概念的理解:①有两个变量;②一个变量的数值随着另一个变量的数值的变化而发生变化;③对于自变量的每一个确定的值,函数值有且只有一个值与之对应.
21.父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
距离地面高度(千米)h 0 1 2 3 4 5
温度(℃)t 20 14 8 2 ﹣4 ﹣10
根据表中,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)表中自变量是 h ;因变量是 t ;当地面上(即h=0时)时,温度是 20 ℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足h与t关系的式子.
(3)计算出距离地面6千米的高空温度是多少?
【分析】(1)根据表格可以得到自变量和因变量,以及h=0时的温度;
(2)根据表格可以得到t与h的关系式;
(3)将h=6代入(2)中的关系式,即可解答本题.
【解答】解:(1)由图可知,
表中自变量是h,因变量是t,
当h=0时,t=20,
故答案为:h,t,20;
(2)设h=kt+b,
,得
即h与t关系是:h=;
(3)当h=6时,6=,
解得,t=﹣16,
即距离地面6千米的高空温度是﹣16℃.
【点评】本题考查函数关系式、常量与变量、函数值,解题的关键是明确题意,找出所求问题需要的条件.
22.物体自由下落的高度h(米)和下落时间t(秒)的关系是:在地球上大约是h=4.9t2,在月球上大约是h=0.8t2,当h=20米时,
(1)物体在地球上和在月球上自由下落的时间各是多少?
(2)物体在哪里下落得快?
【分析】(1)把h=20代入函数解析式分别计算即可得解;
(2)根据速度=路程÷时间分别求出速度,然后比较大小即可.
【解答】解:(1)h=20米时,地球上,4.9t2=20,
解得t=,
月球上,0.8t2=20,
解得t=5;
(2)在地球上的速度==7m/s,
在月球上的速度==4m/s,
所以,在地球上物体下落的快.
【点评】本题考查了函数值的求解,准确计算是解题的关键.
23.已知y=(m+1)x2﹣|m|+n+4
(1)当m、n取何值时,y是x的一次函数?
(2)当m、n取何值时,y是x的正比例函数?
【分析】(1)根据一次函数的定义:一般地,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数,据此求解即可;
(2)根据正比例函数的定义:一般地,形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数,据此求解即可.
【解答】解:(1)根据一次函数的定义,得:2﹣|m|=1,
解得m=±1.
又∵m+1≠0即m≠﹣1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)根据正比例函数的定义,得:2﹣|m|=1,n+4=0,
解得m=±1,n=﹣4,
又∵m+1≠0即m≠﹣1,
∴当m=1,n=﹣4时,这个函数是正比例函数.
【点评】本题主要考查了一次函数与正比例函数的定义,比较简单.一次函数解析式y=kx+b的结构特征:k≠0;自变量的次数为1;常数项b可以为任意实数.正比例函数y=kx的解析式中,比例系数k是常数,k≠0,自变量的次数为1.
24.已知函数y=(m+1)x2﹣|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
【分析】(1)直接利用一次函数的定义分析得出答案;
(2)直接利用正比例函数的定义分析得出答案
【解答】解:(1)根据一次函数的定义,得:
2﹣|m|=1,
解得:m=±1.
又∵m+1≠0即m≠﹣1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)根据正比例函数的定义,得:
2﹣|m|=1,n+4=0,
解得:m=±1,n=﹣4,
又∵m+1≠0即m≠﹣1,
∴当m=1,n=﹣4时,这个函数是正比例函数.
【点评】此题主要考查了一次函数以及正比例函数的定义,正确把握次数与系数的关系是解题关键.
25.在同一坐标系中,画出函数y=﹣2x与y=x+1的图象.
【分析】用两点法画函数的图象即可,取函数上的两点是一般采用的是函数与x、y轴的交点.
【解答】解:根据正比例函数的性质,y=﹣2x过(0,0);再任取函数图象上一点(1,﹣2)即可.
易得y=x+1与坐标轴的交点(0,1)(﹣2,0).
【点评】用两点法画一次函数的图象,一般是先确定两点(常用的是函数与x,y轴的交点),然后描点,连线画出直线即可.
26.先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
(1)正比例函数y=2x过( 0, 0 )和( 1, 2 )
(2)一次函数y=﹣x+3过( 0, 3 )和( 3 ,0 )
【分析】(1)分别将x=0和x=1代入y=2x中求出与之对应的y值,再描点连线即可画出正比例函数y=2x的图象;
(2)分别将x=0、y=0代入y=﹣x+3中求出与之对应的y、x的值,再描点连线即可画出一次函数y=﹣x+3的图象.
【解答】解:(1)当x=0时,y=2x=0,
∴正比例函数y=2x过(0,0);
当x=1时,y=2x=1,
∴正比例函数y=2x过(1,2).
故答案为:0;2.
(2)当x=0时,y=﹣x+3=3,
∴一次函数y=﹣x+3过(0,3);
当y=0时,有﹣x+3=0,
解得:x=3,
∴一次函数y=﹣x+3过(3,0).
故答案为:3;3.
【点评】本题考查了正比例函数的图象、一次函数的图象以及一次函数图象上点的坐标特征,解题的关键是:(1)分别将x=0和x=1代入y=2x中求出与之对应的y值;(2)分别将x=0、y=0代入y=﹣x+3中求出与之对应的y、x的值.
一.选择题(共10小题)
1.以固定的速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球的运动的时间t(秒)之间的关系式是h=v0t﹣4.9t2,在这个关系式中,常量、变量分别为( )
A.4.9是常量,t、h是变量
B.v0是常量,t、h是变量
C.v0、﹣4.9是常量,t、h是变量
D.4.9是常量,v0、t、h是变量
2.下列各曲线表示的y与x的关系中,y不是x的函数的是( )
A. B.
C. D.
3.某商场自行车存放处每周的存车量为5000辆次,其中变速车存车费是每辆一次1元,普通车存车费为每辆一次0.5元,若普通车存车量为x辆次,存车的总收入为y元,则y与x之间的关系式是( )
A.y=0.5x+5000 B.y=0.5x+2500
C.y=﹣0.5x+5000 D.y=﹣0.5x+2500
4.函数y=的自变量x的取值范围是( )
A.x>2 B.x≥2 C.x≠2 D.x≤2
5.若函数,则当自变量x取1,2,3,…,100这100个自然数时,函数值的和是( )
A.540 B.390 C.194 D.197
6.若函数y=(m﹣1)x|m|﹣5是一次函数,则m的值为( )
A.±1 B.﹣1 C.1 D.2
7.若y=(m﹣2)x+(m2﹣4)是正比例函数,则m的取值是( )
A.2 B.﹣2 C.±2 D.任意实数
8.正比例函数y=kx(k≠0)函数值y随x的增大而增大,则y=kx﹣k的图象大致是( )
A. B.
C. D.
9.如图,在同一平面直角坐标系中,表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且mn≠0)图象的是( )
A. B.
C. D.
10.关于一次函数y=﹣2x+3,下列结论正确的是( )
A.图象过点(1,﹣1) B.图象经过一、二、三象限
C.y随x的增大而增大 D.当x>时,y<0
二.填空题(共8小题)
11.在圆的周长公式C=2πr中,变量是 , ,常量是 .
12.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系是 .
13.函数中,自变量x的取值范围是 .
14.函数y=,则当函数值x=﹣1时,y= .
15.已知函数y=(m﹣2)x|m﹣1|+2是关于x的一次函数,则m=
16.当m= 时,函数y=(2m﹣1)x3m﹣2是正比例函数.
17.若函数y=kx+b(k,b为常数)的图象如下图所示,那么当y>0时,x的取值范围是 .
18.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为 .
三.解答题(共8小题)
19.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
20.已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x … 1 2 3 5 7 9 …
y … 1.98 3.95 2.63 1.58 1.13 0.88 …
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为 ;
②该函数的一条性质: .
21.父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
距离地面高度(千米)h 0 1 2 3 4 5
温度(℃)t 20 14 8 2 ﹣4 ﹣10
根据表中,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)表中自变量是 ;因变量是 ;当地面上(即h=0时)时,温度是 ℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足h与t关系的式子.
(3)计算出距离地面6千米的高空温度是多少?
22.物体自由下落的高度h(米)和下落时间t(秒)的关系是:在地球上大约是h=4.9t2,在月球上大约是h=0.8t2,当h=20米时,
(1)物体在地球上和在月球上自由下落的时间各是多少?
(2)物体在哪里下落得快?
23.已知y=(m+1)x2﹣|m|+n+4
(1)当m、n取何值时,y是x的一次函数?
(2)当m、n取何值时,y是x的正比例函数?
24.已知函数y=(m+1)x2﹣|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
25.在同一坐标系中,画出函数y=﹣2x与y=x+1的图象.
26.先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
(1)正比例函数y=2x过( 0, )和( 1, )
(2)一次函数y=﹣x+3过( 0, )和( ,0 )
2020年沪科新版八年级上册数学《第12章 一次函数》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.以固定的速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球的运动的时间t(秒)之间的关系式是h=v0t﹣4.9t2,在这个关系式中,常量、变量分别为( )
A.4.9是常量,t、h是变量
B.v0是常量,t、h是变量
C.v0、﹣4.9是常量,t、h是变量
D.4.9是常量,v0、t、h是变量
【分析】根据在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量,即可答题.
【解答】解:h=v0t﹣4.9t2中的v0(米/秒)是固定的速度,﹣4.9是定值,
故v0和﹣4.9是常量,t、h是变量,
故选:C.
【点评】本题考查了常量与变量的知识,属于基础题,变量是指在程序的运行过程中随时可以发生变化的量.
2.下列各曲线表示的y与x的关系中,y不是x的函数的是( )
A. B.
C. D.
【分析】根据函数的意义即可求出答案.函数的意义反映在图象上简单的判断方法是:做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点.
【解答】解:根据函数的意义可知:对于自变量x的任何值,y都有唯一的值与之相对应,所以只有选项C不满足条件.
故选:C.
【点评】本题主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
3.某商场自行车存放处每周的存车量为5000辆次,其中变速车存车费是每辆一次1元,普通车存车费为每辆一次0.5元,若普通车存车量为x辆次,存车的总收入为y元,则y与x之间的关系式是( )
A.y=0.5x+5000 B.y=0.5x+2500
C.y=﹣0.5x+5000 D.y=﹣0.5x+2500
【分析】根据题意可以写出题目中的函数解关系式,从而可以解答本题.
【解答】解:由题意可得,
y=0.5x+(5000﹣x)×1=﹣0.5x+5000,
故选:C.
【点评】本题考查函数关系式,解答本题的关键是明确题意,写出题目中的函数关系式.
4.函数y=的自变量x的取值范围是( )
A.x>2 B.x≥2 C.x≠2 D.x≤2
【分析】根据被开方数为非负数列出不等式,解之可得.
【解答】解:根据题意知x﹣2≥0,
解得:x≥2,
故选:B.
【点评】本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.
5.若函数,则当自变量x取1,2,3,…,100这100个自然数时,函数值的和是( )
A.540 B.390 C.194 D.197
【分析】将x2﹣100x+196分解为:(x﹣2)(x﹣98),然后可得当2≤x≤98时函数值为0,再分别求出x=1,99,100时的函数值即可.
【解答】解:∵x2﹣100x+196=(x﹣2)(x﹣98)
∴当2≤x≤98时,|x2﹣100x+196|=﹣(x2﹣100x+196),
当自变量x取2到98时函数值为0,
而当x取1,99,100时,|x2﹣100x+196|=x2﹣100x+196,
所以,所求和为(1﹣2)(1﹣98)+(99﹣2)(99﹣98)+(100﹣2)(100﹣98)=97+97+196=390.
故选:B.
【点评】本题考查函数值的知识,有一定难度,关键是将x2﹣100x+196分解为:(x﹣2)(x﹣98)进行解答.
6.若函数y=(m﹣1)x|m|﹣5是一次函数,则m的值为( )
A.±1 B.﹣1 C.1 D.2
【分析】根据一次函数的定义列式计算即可得解.
【解答】解:根据题意得,|m|=1且m﹣1≠0,
解得m=±1且m≠1,
所以,m=﹣1.
故选:B.
【点评】本题主要考查了一次函数的定义,一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.
7.若y=(m﹣2)x+(m2﹣4)是正比例函数,则m的取值是( )
A.2 B.﹣2 C.±2 D.任意实数
【分析】正比例函数的一般式y=kx,k≠0,所以使m2﹣4=0,m﹣2≠0即可得解.
【解答】解:根据题意得:;
得:m=﹣2.
故选:B.
【点评】考查了正比例函数的定义,比较简单.
8.正比例函数y=kx(k≠0)函数值y随x的增大而增大,则y=kx﹣k的图象大致是( )
A. B.
C. D.
【分析】直接利用正比例函数的性质得出k的取值范围,进而得出一次函数经过的象限.
【解答】解:∵正比例函数y=kx(k≠0)函数值y随x的增大而增大,
∴k>0,
∴y=kx﹣k的图象经过第一、三、四象限,
故选:B.
【点评】此题主要考查了一次函数与正比例函数的图象,正确得出k的符号是解题关键.
9.如图,在同一平面直角坐标系中,表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且mn≠0)图象的是( )
A. B.
C. D.
【分析】根据“两数相乘,同号得正,异号得负”分两种情况讨论mn的符号,然后根据m、n同正时,同负时,一正一负或一负一正时,利用一次函数的性质进行判断.
【解答】解:①当mn>0,m,n同号,同正时y=mx+n过第一,二,三象限,同负时过二,三,四象限;
②当mn<0时,m,n异号,则y=mx+n过一,三,四象限或一,二,四象限.
y=mnx过原点,二、四象限.由题意m,n是常数,且mn<0.
故选:A.
【点评】此题主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.
一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
10.关于一次函数y=﹣2x+3,下列结论正确的是( )
A.图象过点(1,﹣1) B.图象经过一、二、三象限
C.y随x的增大而增大 D.当x>时,y<0
【分析】A、把点的坐标代入关系式,检验是否成立;
B、根据系数的性质判断,或画出草图判断;
C、根据一次项系数判断;
D、可根据函数图象判断,亦可解不等式求解.
【解答】解:A、当x=1时,y=1.所以图象不过(1,﹣1),故错误;
B、∵﹣2<0,3>0,
∴图象过一、二、四象限,故错误;
C、∵﹣2<0,
∴y随x的增大而减小,故错误;
D、画出草图.
∵当x>时,图象在x轴下方,
∴y<0,故正确.
故选:D.
【点评】本题主要考查了一次函数的性质以及一次函数与方程、不等式的关系.常采用数形结合的方法求解.
二.填空题(共8小题)
11.在圆的周长公式C=2πr中,变量是 C , r ,常量是 2π .
【分析】根据函数的意义可知:变量是改变的量,常量是不变的量,据此即可确定变量与常量.
【解答】解:∵在圆的周长公式C=2πr中,C与r是改变的,π是不变的;
∴变量是C,r,常量是2π.
【点评】主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
12.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系是 h=n+6 .
【分析】根据等量关系,可得方程组,根据解方程组,可得纸杯的高,纸杯边沿的高,根据纸杯的高加纸杯边沿的高,可得答案.
【解答】解:设纸杯的高是x,纸杯边沿的高是y,由题意,得
,
解得.
高度h与n的函数关系是 h=(n﹣1)+7,
即h=n+6,
故答案为:h=n+6.
【点评】本题考查了函数关系式,利用方程组得出纸杯的高、纸杯边沿的高是解题关键.
13.函数中,自变量x的取值范围是 x≥﹣4 .
【分析】根据二次根式的性质,被开方数大于等于0,就可以求解.
【解答】解:根据题意得:x+4≥0,
解得:x≥﹣4.
故答案为:x≥﹣4.
【点评】本题考查的是函数自变量取值范围的求法.函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数为非负数.
14.函数y=,则当函数值x=﹣1时,y= 6 .
【分析】把x=﹣1代入第一个关系式进行计算即可得解.
【解答】解:x=﹣1时,
y=2x2+4
=2×(﹣1)2+4
=2+4
=6.
故答案为:6.
【点评】本题考查了函数值求解,是基础题,根据x的取值范围确定出函数关系式是解题的关键.
15.已知函数y=(m﹣2)x|m﹣1|+2是关于x的一次函数,则m= 0
【分析】根据一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1,即可得出m的值.
【解答】解:根据一次函数的定义可得:m﹣2≠0,|m﹣1|=1,
由|m﹣1|=1,解得:m=0或2,
又m﹣2≠0,m≠2,
∴m=0.
故答案为:0.
【点评】本题主要考查了一次函数的定义,难度不大,注意基础概念的掌握.
16.当m= 1 时,函数y=(2m﹣1)x3m﹣2是正比例函数.
【分析】直接利用正比例函数的定义得出3m﹣2=1,进而得出答案.
【解答】解:∵函数y=(2m﹣1)x3m﹣2是正比例函数,
∴3m﹣2=1,
解得:m=1.
故答案为:1.
【点评】此题主要考查了正比例函数的定义,正确把握定义是解题关键.
17.若函数y=kx+b(k,b为常数)的图象如下图所示,那么当y>0时,x的取值范围是 x<2 .
【分析】根据一次函数图象的性质利用数形结合可直接解答.
【解答】解:∵由一次函数的图象可知,当x<2时函数的图象在x轴的上方,
∴当y>0时,x的取值范围是x<2.
故答案为:x<2.
【点评】本题考查的是一次函数的图象,利用数形结合求出x的取值范围是解答此题的关键.
18.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为 a<c<b .
【分析】根据直线所过象限可得a<0,b>0,c>0,再根据直线陡的情况可判断出b>c,进而得到答案.
【解答】解:根据三个函数图象所在象限可得a<0,b>0,c>0,
再根据直线越陡,|k|越大,则b>c.
则b>c>a,
故答案为:a<c<b.
【点评】此题主要考查了正比例函数图象,关键是掌握:当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.同时注意直线越陡,则|k|越大
三.解答题(共8小题)
19.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
【分析】根据总价=单价×数量,可得函数关系式.
【解答】解:由题意得:
y=2x,
常量是2,变量是x、y,
x是自变量,y是x的函数.
【点评】主要考查了常量与变量.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
20.已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x … 1 2 3 5 7 9 …
y … 1.98 3.95 2.63 1.58 1.13 0.88 …
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为 2 ;
②该函数的一条性质: 该函数有最大值 .
【分析】(1)按照自变量由小到大,利用平滑的曲线连结各点即可;
(2)①在所画的函数图象上找出自变量为4所对应的函数值即可;
②利用函数图象有最高点求解.
【解答】解:(1)如图,
(2)①x=4对应的函数值y约为2.0;
②该函数有最大值.
故答案为2,该函数有最大值.
【点评】本题考查了函数的定义:对于函数概念的理解:①有两个变量;②一个变量的数值随着另一个变量的数值的变化而发生变化;③对于自变量的每一个确定的值,函数值有且只有一个值与之对应.
21.父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
距离地面高度(千米)h 0 1 2 3 4 5
温度(℃)t 20 14 8 2 ﹣4 ﹣10
根据表中,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)表中自变量是 h ;因变量是 t ;当地面上(即h=0时)时,温度是 20 ℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足h与t关系的式子.
(3)计算出距离地面6千米的高空温度是多少?
【分析】(1)根据表格可以得到自变量和因变量,以及h=0时的温度;
(2)根据表格可以得到t与h的关系式;
(3)将h=6代入(2)中的关系式,即可解答本题.
【解答】解:(1)由图可知,
表中自变量是h,因变量是t,
当h=0时,t=20,
故答案为:h,t,20;
(2)设h=kt+b,
,得
即h与t关系是:h=;
(3)当h=6时,6=,
解得,t=﹣16,
即距离地面6千米的高空温度是﹣16℃.
【点评】本题考查函数关系式、常量与变量、函数值,解题的关键是明确题意,找出所求问题需要的条件.
22.物体自由下落的高度h(米)和下落时间t(秒)的关系是:在地球上大约是h=4.9t2,在月球上大约是h=0.8t2,当h=20米时,
(1)物体在地球上和在月球上自由下落的时间各是多少?
(2)物体在哪里下落得快?
【分析】(1)把h=20代入函数解析式分别计算即可得解;
(2)根据速度=路程÷时间分别求出速度,然后比较大小即可.
【解答】解:(1)h=20米时,地球上,4.9t2=20,
解得t=,
月球上,0.8t2=20,
解得t=5;
(2)在地球上的速度==7m/s,
在月球上的速度==4m/s,
所以,在地球上物体下落的快.
【点评】本题考查了函数值的求解,准确计算是解题的关键.
23.已知y=(m+1)x2﹣|m|+n+4
(1)当m、n取何值时,y是x的一次函数?
(2)当m、n取何值时,y是x的正比例函数?
【分析】(1)根据一次函数的定义:一般地,形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数,据此求解即可;
(2)根据正比例函数的定义:一般地,形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数,据此求解即可.
【解答】解:(1)根据一次函数的定义,得:2﹣|m|=1,
解得m=±1.
又∵m+1≠0即m≠﹣1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)根据正比例函数的定义,得:2﹣|m|=1,n+4=0,
解得m=±1,n=﹣4,
又∵m+1≠0即m≠﹣1,
∴当m=1,n=﹣4时,这个函数是正比例函数.
【点评】本题主要考查了一次函数与正比例函数的定义,比较简单.一次函数解析式y=kx+b的结构特征:k≠0;自变量的次数为1;常数项b可以为任意实数.正比例函数y=kx的解析式中,比例系数k是常数,k≠0,自变量的次数为1.
24.已知函数y=(m+1)x2﹣|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
【分析】(1)直接利用一次函数的定义分析得出答案;
(2)直接利用正比例函数的定义分析得出答案
【解答】解:(1)根据一次函数的定义,得:
2﹣|m|=1,
解得:m=±1.
又∵m+1≠0即m≠﹣1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)根据正比例函数的定义,得:
2﹣|m|=1,n+4=0,
解得:m=±1,n=﹣4,
又∵m+1≠0即m≠﹣1,
∴当m=1,n=﹣4时,这个函数是正比例函数.
【点评】此题主要考查了一次函数以及正比例函数的定义,正确把握次数与系数的关系是解题关键.
25.在同一坐标系中,画出函数y=﹣2x与y=x+1的图象.
【分析】用两点法画函数的图象即可,取函数上的两点是一般采用的是函数与x、y轴的交点.
【解答】解:根据正比例函数的性质,y=﹣2x过(0,0);再任取函数图象上一点(1,﹣2)即可.
易得y=x+1与坐标轴的交点(0,1)(﹣2,0).
【点评】用两点法画一次函数的图象,一般是先确定两点(常用的是函数与x,y轴的交点),然后描点,连线画出直线即可.
26.先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
(1)正比例函数y=2x过( 0, 0 )和( 1, 2 )
(2)一次函数y=﹣x+3过( 0, 3 )和( 3 ,0 )
【分析】(1)分别将x=0和x=1代入y=2x中求出与之对应的y值,再描点连线即可画出正比例函数y=2x的图象;
(2)分别将x=0、y=0代入y=﹣x+3中求出与之对应的y、x的值,再描点连线即可画出一次函数y=﹣x+3的图象.
【解答】解:(1)当x=0时,y=2x=0,
∴正比例函数y=2x过(0,0);
当x=1时,y=2x=1,
∴正比例函数y=2x过(1,2).
故答案为:0;2.
(2)当x=0时,y=﹣x+3=3,
∴一次函数y=﹣x+3过(0,3);
当y=0时,有﹣x+3=0,
解得:x=3,
∴一次函数y=﹣x+3过(3,0).
故答案为:3;3.
【点评】本题考查了正比例函数的图象、一次函数的图象以及一次函数图象上点的坐标特征,解题的关键是:(1)分别将x=0和x=1代入y=2x中求出与之对应的y值;(2)分别将x=0、y=0代入y=﹣x+3中求出与之对应的y、x的值.
