苏科版七年级数学下册第7章 平面图形的认识(二)专题训练(一) 平行线的判定与性质的综合应用含答案
文档属性
| 名称 | 苏科版七年级数学下册第7章 平面图形的认识(二)专题训练(一) 平行线的判定与性质的综合应用含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 341.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-07 10:49:45 | ||
图片预览



文档简介
专题训练(一) 平行线的判定与性质的综合应用
? 应用一 求角的度数
1.2019·济宁 如图1-ZT-1,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数是( )
A.65° B.60° C.55° D.75°
图1-ZT-1
2.如图1-ZT-2,∠1=∠2=40°,MN平分∠EMB,则∠3=________°.
图1-ZT-2
3.如图1-ZT-3,∠DAB+∠D=180°,AC平分∠DAB,分别交BF,DC于点E,C,且∠CAD=25°,求∠C的度数.
图1-ZT-3
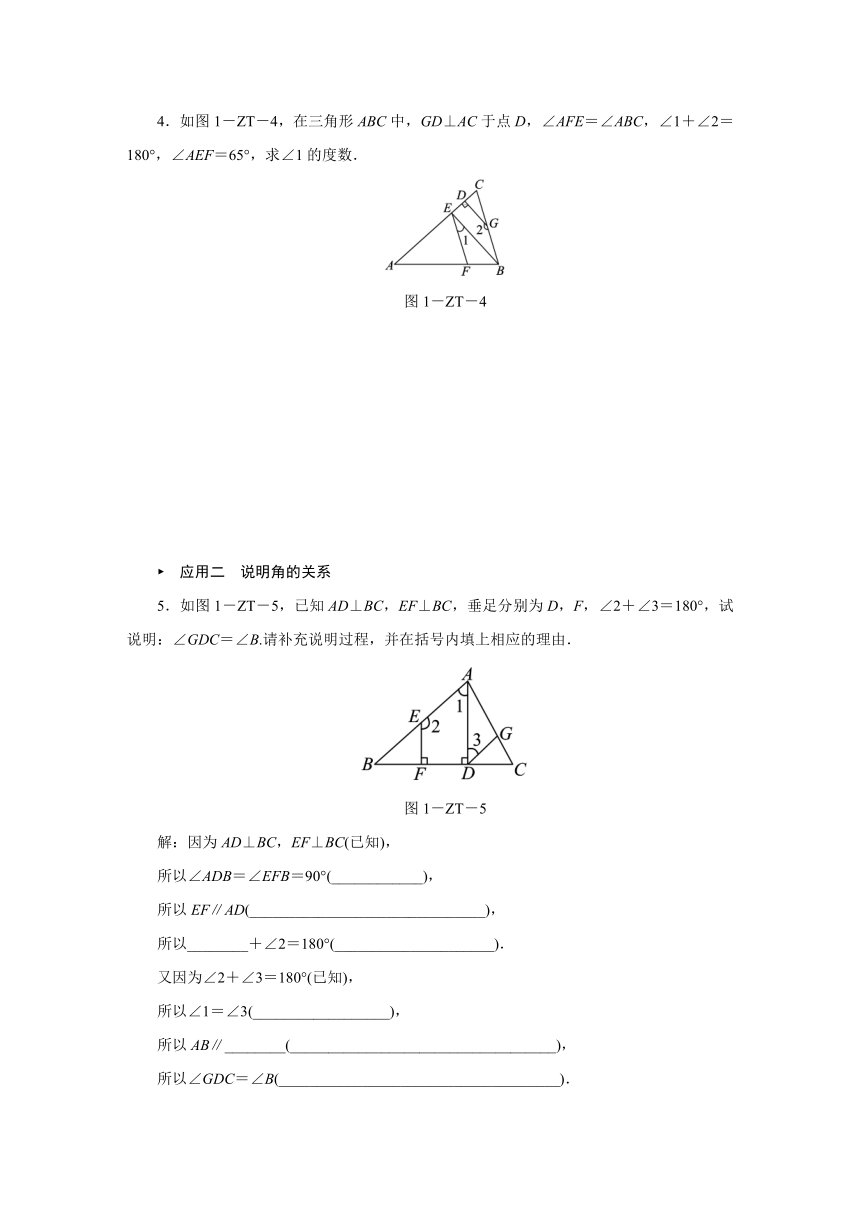
4.如图1-ZT-4,在三角形ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180°,∠AEF=65°,求∠1的度数.
图1-ZT-4
? 应用二 说明角的关系
5.如图1-ZT-5,已知AD⊥BC,EF⊥BC,垂足分别为D,F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
图1-ZT-5
解:因为AD⊥BC,EF⊥BC(已知),
所以∠ADB=∠EFB=90°(____________),
所以EF∥AD(_______________________________),
所以________+∠2=180°(_____________________).
又因为∠2+∠3=180°(已知),
所以∠1=∠3(__________________),
所以AB∥________(___________________________________),
所以∠GDC=∠B(_____________________________________).
6.如图1-ZT-6,直线CD,EF被直线OA,OB所截,∠1+∠2=180°.试说明:∠3=∠4.
图1-ZT-6
7.如图1-ZT-7,已知点E在线段AD上,点P在直线CD上,∠AEF=∠F,∠BAD=∠CPF.试说明:∠ABD+∠BDC=180°.
图1-ZT-7
8.如图1-ZT-8,∠ABE+∠DEB=180°,∠1=∠2,则∠F与∠G的大小关系如何?请说明理由.
图1-ZT-8
9.如图1-ZT-9,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A=∠F成立吗?请说明理由.
图1-ZT-9
? 应用三 说明直线之间的位置关系
10.如图1-ZT-10,在四边形ABCD中,E,F分别是CD,AB延长线上的点,连接EF,分别交AD,BC于点G,H.若∠1=∠2,∠A=∠C,试说明AD∥BC和AB∥CD.
图1-ZT-10
下面是小明的解答过程,请在横线上填写推理依据.
解:因为∠1=∠2(________),
∠1=∠AGH(____________),
所以∠2=∠AGH(__________),
所以AD∥BC(______________________),
所以∠ADE=∠C(______________________).
因为∠A=∠C(________),
所以∠ADE=∠A(____________),
所以AB∥CD(______________________).
11.2018·益阳 如图1-ZT-11,AB∥CD,∠1=∠2.试说明:AM∥CN.
图1-ZT-11
12.如图1-ZT-12,AD∥BC,∠DAC=120°,∠ACF=20°,∠EFC=140°.试说明:EF∥BC.
图1-ZT-12
教师详解详析
1.[解析] C 如图,因为∠1=∠2,所以a∥b,所以∠4=∠5.因为∠5=180°-∠3=55°,
所以∠4=55°.故选C.
2.[答案] 110
[解析] 因为∠2=∠MEN,∠1=∠2=40°,
所以∠1=∠MEN,
所以AB∥CD,
所以∠3+∠BMN=180°.
因为MN平分∠EMB,
所以∠BMN=70°,
所以∠3=180°-70°=110°.故答案为110.
3.解:因为AC平分∠DAB,
所以∠DAC=∠BAC=25°.
因为∠DAB+∠D=180°,所以AB∥DC,
所以∠C=∠BAC=25°.
4.解:因为∠AFE=∠ABC(已知),
所以EF∥BC(同位角相等,两直线平行),
所以∠1=∠EBC(两直线平行,内错角相等).
因为∠1+∠2=180°(已知),
所以∠EBC+∠2=180°(等量代换),
所以EB∥DG(同旁内角互补,两直线平行),
所以∠GDE=∠BEA(两直线平行,同位角相等).
因为GD⊥AC(已知),
所以∠GDE=90°(垂直的定义),
所以∠BEA=90°(两直线平行,同位角相等).
因为∠AEF=65°(已知),
所以∠1=∠BEA-∠AEF=90°-65°=25°(等式的性质).
5.垂直的定义 同位角相等,两直线平行 ∠1 两直线平行,同旁内角互补 同角的补角相等 DG 内错角相等,两直线平行 两直线平行,同位角相等
6.解:如图,因为∠2与∠5是对顶角,所以∠2=∠5.
因为∠1+∠2=180°,
所以∠1+∠5=180°,
所以CD∥EF,
所以∠3=∠4.
7.解:因为∠AEF=∠F,所以PF∥AD,
所以∠ADC=∠CPF.
又因为∠BAD=∠CPF,所以∠BAD=∠ADC,
所以AB∥CD,所以∠ABD+∠BDC=180°.
8.解:∠F=∠G.
理由:因为∠ABE+∠DEB=180°,
所以AC∥ED,所以∠CBE=∠DEB.
因为∠1=∠2,所以∠CBE-∠1=∠DEB-∠2,
即∠FBE=∠GEB,
所以BF∥EG,所以∠F=∠G.
9.解:∠A=∠F成立.
理由:因为∠AGB=∠EHF,∠AGB=∠DGH,
所以∠EHF=∠DGH,所以BD∥CE,
所以∠C=∠ABD.
又因为∠C=∠D,所以∠ABD=∠D,
所以AC∥DF,所以∠A=∠F.
10.已知 对顶角相等 等量代换 同位角相等,两直线平行 两直线平行,同位角相等 已知
等量代换 内错角相等,两直线平行
11.解:因为AB∥CD,所以∠EAB=∠ECD.
因为∠1=∠2,所以∠EAM=∠ECN,
所以AM∥CN.
12.解:因为AD∥BC,
所以∠DAC+∠ACB=180°.
因为∠DAC=120°,
所以∠ACB=60°.
又因为∠ACF=20°,
所以∠BCF=∠ACB-∠ACF=40°.
又因为∠EFC=140°,
所以∠BCF+∠EFC=180°,
所以EF∥BC.
? 应用一 求角的度数
1.2019·济宁 如图1-ZT-1,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数是( )
A.65° B.60° C.55° D.75°
图1-ZT-1
2.如图1-ZT-2,∠1=∠2=40°,MN平分∠EMB,则∠3=________°.
图1-ZT-2
3.如图1-ZT-3,∠DAB+∠D=180°,AC平分∠DAB,分别交BF,DC于点E,C,且∠CAD=25°,求∠C的度数.
图1-ZT-3
4.如图1-ZT-4,在三角形ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180°,∠AEF=65°,求∠1的度数.
图1-ZT-4
? 应用二 说明角的关系
5.如图1-ZT-5,已知AD⊥BC,EF⊥BC,垂足分别为D,F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
图1-ZT-5
解:因为AD⊥BC,EF⊥BC(已知),
所以∠ADB=∠EFB=90°(____________),
所以EF∥AD(_______________________________),
所以________+∠2=180°(_____________________).
又因为∠2+∠3=180°(已知),
所以∠1=∠3(__________________),
所以AB∥________(___________________________________),
所以∠GDC=∠B(_____________________________________).
6.如图1-ZT-6,直线CD,EF被直线OA,OB所截,∠1+∠2=180°.试说明:∠3=∠4.
图1-ZT-6
7.如图1-ZT-7,已知点E在线段AD上,点P在直线CD上,∠AEF=∠F,∠BAD=∠CPF.试说明:∠ABD+∠BDC=180°.
图1-ZT-7
8.如图1-ZT-8,∠ABE+∠DEB=180°,∠1=∠2,则∠F与∠G的大小关系如何?请说明理由.
图1-ZT-8
9.如图1-ZT-9,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A=∠F成立吗?请说明理由.
图1-ZT-9
? 应用三 说明直线之间的位置关系
10.如图1-ZT-10,在四边形ABCD中,E,F分别是CD,AB延长线上的点,连接EF,分别交AD,BC于点G,H.若∠1=∠2,∠A=∠C,试说明AD∥BC和AB∥CD.
图1-ZT-10
下面是小明的解答过程,请在横线上填写推理依据.
解:因为∠1=∠2(________),
∠1=∠AGH(____________),
所以∠2=∠AGH(__________),
所以AD∥BC(______________________),
所以∠ADE=∠C(______________________).
因为∠A=∠C(________),
所以∠ADE=∠A(____________),
所以AB∥CD(______________________).
11.2018·益阳 如图1-ZT-11,AB∥CD,∠1=∠2.试说明:AM∥CN.
图1-ZT-11
12.如图1-ZT-12,AD∥BC,∠DAC=120°,∠ACF=20°,∠EFC=140°.试说明:EF∥BC.
图1-ZT-12
教师详解详析
1.[解析] C 如图,因为∠1=∠2,所以a∥b,所以∠4=∠5.因为∠5=180°-∠3=55°,
所以∠4=55°.故选C.
2.[答案] 110
[解析] 因为∠2=∠MEN,∠1=∠2=40°,
所以∠1=∠MEN,
所以AB∥CD,
所以∠3+∠BMN=180°.
因为MN平分∠EMB,
所以∠BMN=70°,
所以∠3=180°-70°=110°.故答案为110.
3.解:因为AC平分∠DAB,
所以∠DAC=∠BAC=25°.
因为∠DAB+∠D=180°,所以AB∥DC,
所以∠C=∠BAC=25°.
4.解:因为∠AFE=∠ABC(已知),
所以EF∥BC(同位角相等,两直线平行),
所以∠1=∠EBC(两直线平行,内错角相等).
因为∠1+∠2=180°(已知),
所以∠EBC+∠2=180°(等量代换),
所以EB∥DG(同旁内角互补,两直线平行),
所以∠GDE=∠BEA(两直线平行,同位角相等).
因为GD⊥AC(已知),
所以∠GDE=90°(垂直的定义),
所以∠BEA=90°(两直线平行,同位角相等).
因为∠AEF=65°(已知),
所以∠1=∠BEA-∠AEF=90°-65°=25°(等式的性质).
5.垂直的定义 同位角相等,两直线平行 ∠1 两直线平行,同旁内角互补 同角的补角相等 DG 内错角相等,两直线平行 两直线平行,同位角相等
6.解:如图,因为∠2与∠5是对顶角,所以∠2=∠5.
因为∠1+∠2=180°,
所以∠1+∠5=180°,
所以CD∥EF,
所以∠3=∠4.
7.解:因为∠AEF=∠F,所以PF∥AD,
所以∠ADC=∠CPF.
又因为∠BAD=∠CPF,所以∠BAD=∠ADC,
所以AB∥CD,所以∠ABD+∠BDC=180°.
8.解:∠F=∠G.
理由:因为∠ABE+∠DEB=180°,
所以AC∥ED,所以∠CBE=∠DEB.
因为∠1=∠2,所以∠CBE-∠1=∠DEB-∠2,
即∠FBE=∠GEB,
所以BF∥EG,所以∠F=∠G.
9.解:∠A=∠F成立.
理由:因为∠AGB=∠EHF,∠AGB=∠DGH,
所以∠EHF=∠DGH,所以BD∥CE,
所以∠C=∠ABD.
又因为∠C=∠D,所以∠ABD=∠D,
所以AC∥DF,所以∠A=∠F.
10.已知 对顶角相等 等量代换 同位角相等,两直线平行 两直线平行,同位角相等 已知
等量代换 内错角相等,两直线平行
11.解:因为AB∥CD,所以∠EAB=∠ECD.
因为∠1=∠2,所以∠EAM=∠ECN,
所以AM∥CN.
12.解:因为AD∥BC,
所以∠DAC+∠ACB=180°.
因为∠DAC=120°,
所以∠ACB=60°.
又因为∠ACF=20°,
所以∠BCF=∠ACB-∠ACF=40°.
又因为∠EFC=140°,
所以∠BCF+∠EFC=180°,
所以EF∥BC.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
