25.2三视图 导学案
图片预览
文档简介
25.2三视图导学案
课题
三视图
单元
25
学科
数学
年级
九年级
知识目标
1.会从投影的角度理解视图的概念;
2.会画三视图以及三视图确定几何体
重点难点
重点:从投影的角度理解三视图,会画几何体的视图.
难点:会结合组合三视图算出面积
教学过程
知识链接
1.正投影
2.正投影的性质
合作探究
一、教材第80页
只看到几何体的一个视图,就能够准确地刻画这个几何体的形状与大小吗?如果已知一个几何体在水平面上的视图是圆,你能断定这个几何体是球吗?为什么?
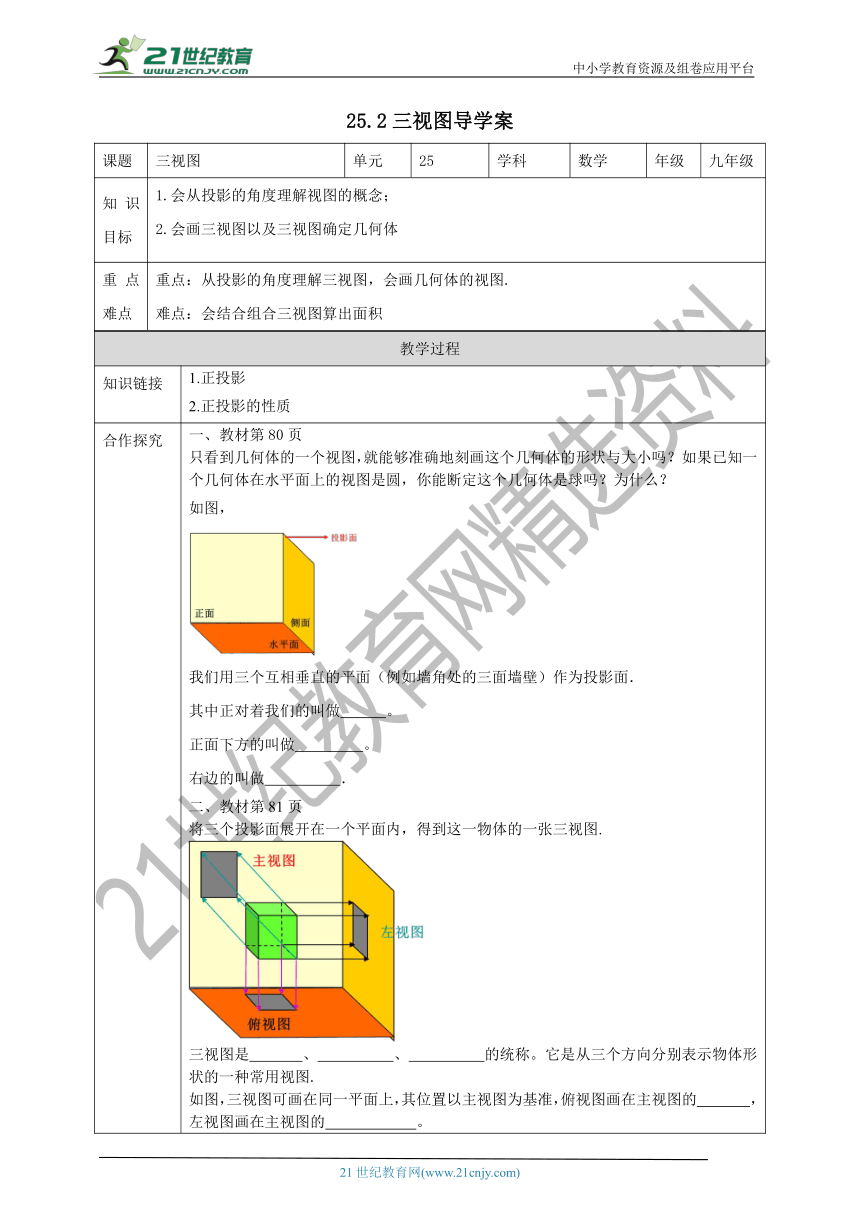
如图,
我们用三个互相垂直的平面(例如墙角处的三面墙壁)作为投影面.
其中正对着我们的叫做 。
正面下方的叫做 。
右边的叫做 .
二、教材第81页
将三个投影面展开在一个平面内,得到这一物体的一张三视图.
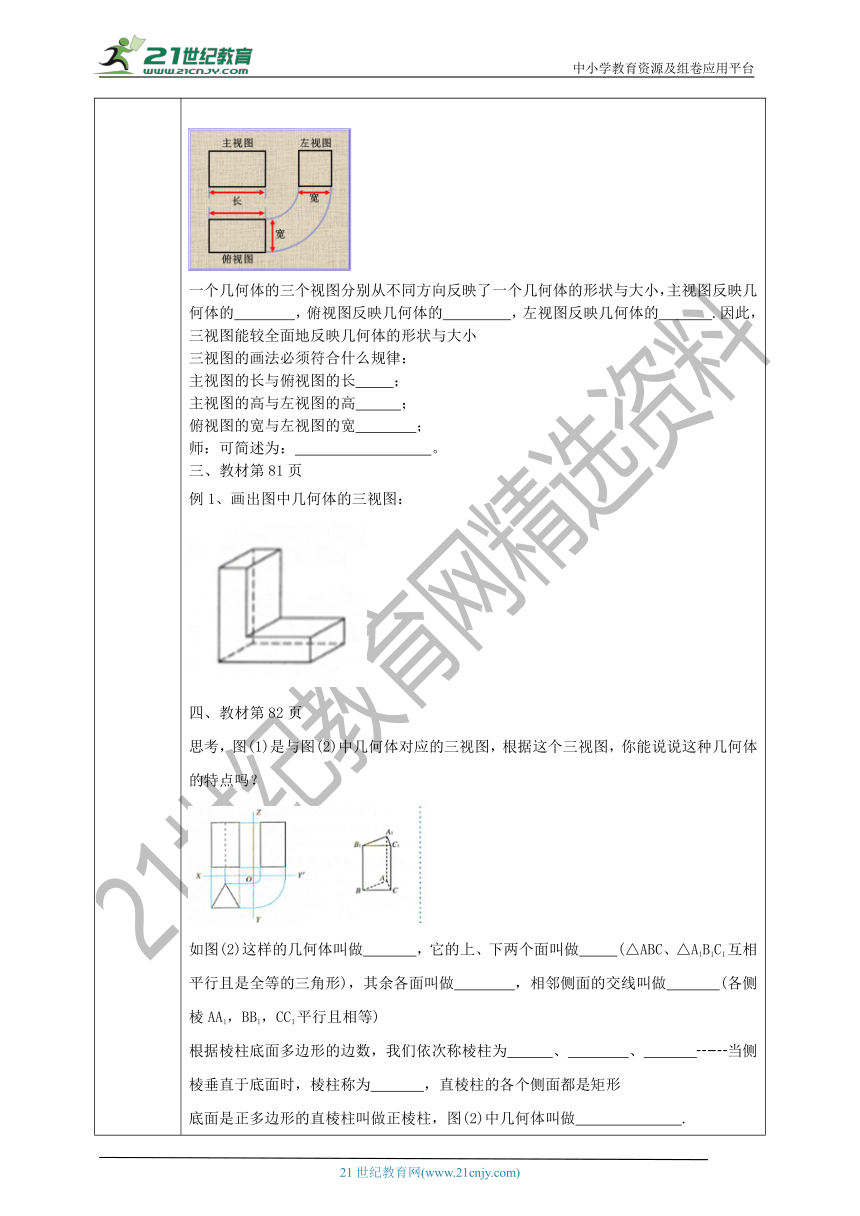
三视图是 、 、 的统称。它是从三个方向分别表示物体形状的一种常用视图.
如图,三视图可画在同一平面上,其位置以主视图为基准,俯视图画在主视图的 ,左视图画在主视图的 。
一个几何体的三个视图分别从不同方向反映了一个几何体的形状与大小,主视图反映几何体的 ,俯视图反映几何体的 ,左视图反映几何体的 .因此,三视图能较全面地反映几何体的形状与大小
三视图的画法必须符合什么规律:
主视图的长与俯视图的长 ;
主视图的高与左视图的高 ;
俯视图的宽与左视图的宽 ;
师:可简述为: 。
三、教材第81页
例1、画出图中几何体的三视图:
四、教材第82页
思考,图(1)是与图(2)中几何体对应的三视图,根据这个三视图,你能说说这种几何体的特点吗?
如图(2)这样的几何体叫做 ,它的上、下两个面叫做 (△ABC、△A1B1C1互相平行且是全等的三角形),其余各面叫做 ,相邻侧面的交线叫做 (各侧棱AA1,BB1,CC1平行且相等)
根据棱柱底面多边形的边数,我们依次称棱柱为 、 、 ┄┄当侧棱垂直于底面时,棱柱称为 ,直棱柱的各个侧面都是矩形
底面是正多边形的直棱柱叫做正棱柱,图(2)中几何体叫做 .
例2、某工厂要加工一批正六棱柱形状的食品盒,其三视图如图.问制作这样一个食品盒所需要硬纸板的面积至少为多少?(精确到1cm2)
自主尝试
1.一个物体的俯视图是圆,则该物体的形状是( )
A.球体 B.圆柱 C.圆锥 D.以上都有可能
2.一个几何体的三种视图如图29-22所示,则这个几何体是( )
A.圆柱 B.圆锥 C.长方体 D.正方体
3.一个物体的正视图、俯视图如图29-23所示,请你画出该物体的左视图并说出该物体形状的名称.
【方法宝典】
根据三视图概念进行解题.
当堂检测
1.将如图所示放置的一个直角三角形ABC(∠C=90°),绕斜边AB旋转一周所得到的几何体的主视图是四个图形中的____________(只填序号).
2.如图所示的物体中,一样的为( )
A.(1)与(2) B.(1)与(3) C.(1)与(4) D.(2)与(3)
3.桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图29-26所示,这个几何体最多可以由___________个这样的正方体组成.
4.将图所示的阴影部分剪下来,围成一个几何体的侧面,使AB、DC重合,则所围成的几何体图形是( )
5.如图所示,说出下列四个图形各是由哪些立体图形展开得到的?
小结反思
通过本节课的学习,你们有什么收获?
参考答案:
当堂检测:
1.(2) 2.A 3.13 4.D 短 5.(1)正方体 (2)圆柱 (3)三棱柱 (4)四棱锥
课题
三视图
单元
25
学科
数学
年级
九年级
知识目标
1.会从投影的角度理解视图的概念;
2.会画三视图以及三视图确定几何体
重点难点
重点:从投影的角度理解三视图,会画几何体的视图.
难点:会结合组合三视图算出面积
教学过程
知识链接
1.正投影
2.正投影的性质
合作探究
一、教材第80页
只看到几何体的一个视图,就能够准确地刻画这个几何体的形状与大小吗?如果已知一个几何体在水平面上的视图是圆,你能断定这个几何体是球吗?为什么?
如图,
我们用三个互相垂直的平面(例如墙角处的三面墙壁)作为投影面.
其中正对着我们的叫做 。
正面下方的叫做 。
右边的叫做 .
二、教材第81页
将三个投影面展开在一个平面内,得到这一物体的一张三视图.
三视图是 、 、 的统称。它是从三个方向分别表示物体形状的一种常用视图.
如图,三视图可画在同一平面上,其位置以主视图为基准,俯视图画在主视图的 ,左视图画在主视图的 。
一个几何体的三个视图分别从不同方向反映了一个几何体的形状与大小,主视图反映几何体的 ,俯视图反映几何体的 ,左视图反映几何体的 .因此,三视图能较全面地反映几何体的形状与大小
三视图的画法必须符合什么规律:
主视图的长与俯视图的长 ;
主视图的高与左视图的高 ;
俯视图的宽与左视图的宽 ;
师:可简述为: 。
三、教材第81页
例1、画出图中几何体的三视图:
四、教材第82页
思考,图(1)是与图(2)中几何体对应的三视图,根据这个三视图,你能说说这种几何体的特点吗?
如图(2)这样的几何体叫做 ,它的上、下两个面叫做 (△ABC、△A1B1C1互相平行且是全等的三角形),其余各面叫做 ,相邻侧面的交线叫做 (各侧棱AA1,BB1,CC1平行且相等)
根据棱柱底面多边形的边数,我们依次称棱柱为 、 、 ┄┄当侧棱垂直于底面时,棱柱称为 ,直棱柱的各个侧面都是矩形
底面是正多边形的直棱柱叫做正棱柱,图(2)中几何体叫做 .
例2、某工厂要加工一批正六棱柱形状的食品盒,其三视图如图.问制作这样一个食品盒所需要硬纸板的面积至少为多少?(精确到1cm2)
自主尝试
1.一个物体的俯视图是圆,则该物体的形状是( )
A.球体 B.圆柱 C.圆锥 D.以上都有可能
2.一个几何体的三种视图如图29-22所示,则这个几何体是( )
A.圆柱 B.圆锥 C.长方体 D.正方体
3.一个物体的正视图、俯视图如图29-23所示,请你画出该物体的左视图并说出该物体形状的名称.
【方法宝典】
根据三视图概念进行解题.
当堂检测
1.将如图所示放置的一个直角三角形ABC(∠C=90°),绕斜边AB旋转一周所得到的几何体的主视图是四个图形中的____________(只填序号).
2.如图所示的物体中,一样的为( )
A.(1)与(2) B.(1)与(3) C.(1)与(4) D.(2)与(3)
3.桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图29-26所示,这个几何体最多可以由___________个这样的正方体组成.
4.将图所示的阴影部分剪下来,围成一个几何体的侧面,使AB、DC重合,则所围成的几何体图形是( )
5.如图所示,说出下列四个图形各是由哪些立体图形展开得到的?
小结反思
通过本节课的学习,你们有什么收获?
参考答案:
当堂检测:
1.(2) 2.A 3.13 4.D 短 5.(1)正方体 (2)圆柱 (3)三棱柱 (4)四棱锥
