7.6 余角、补角 课件(20张)
文档属性
| 名称 | 7.6 余角、补角 课件(20张) |
|
|
| 格式 | zip | ||
| 文件大小 | 191.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 08:41:00 | ||
图片预览






文档简介
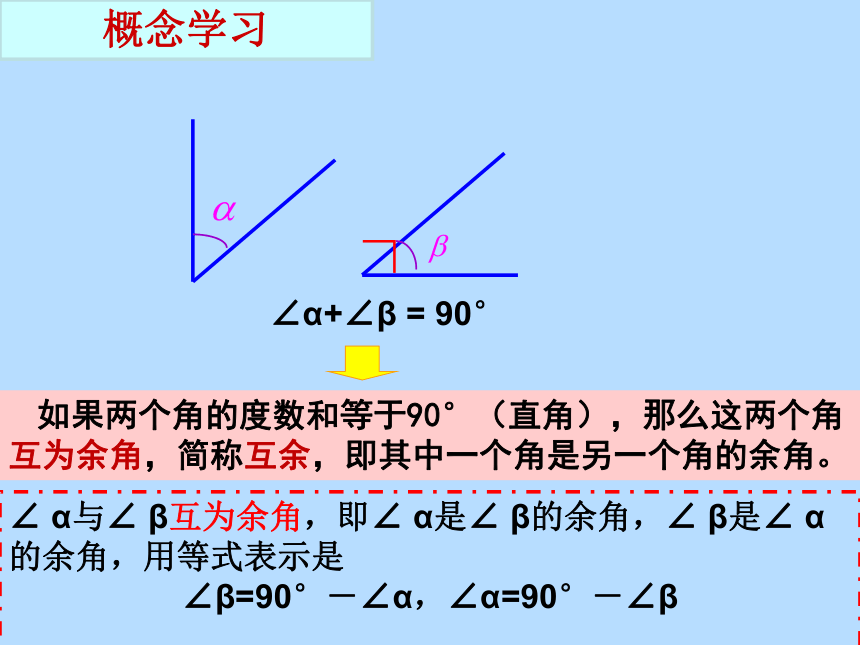
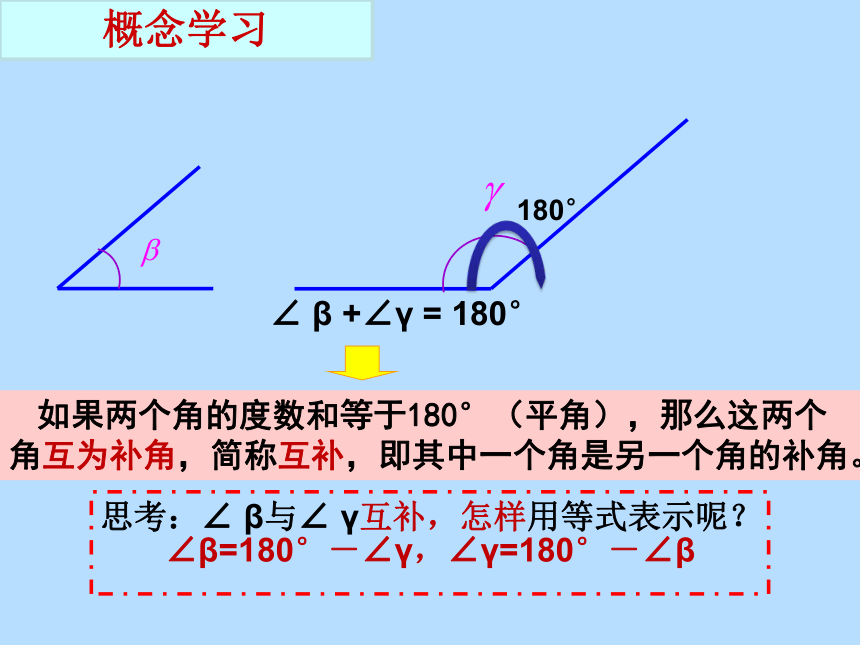
课件20张PPT。∠α+∠β = 90°∟∠ β +∠γ = 180°180°7.6 余角、补角∠α+∠β = 90°如果两个角的度数和等于90°(直角),那么这两个角互为余角,简称互余,即其中一个角是另一个角的余角。 ∟概念学习∠ α与∠ β互为余角,即∠ α是∠ β的余角,∠ β是∠ α的余角,用等式表示是
∠β=90°-∠α,∠α=90°-∠β
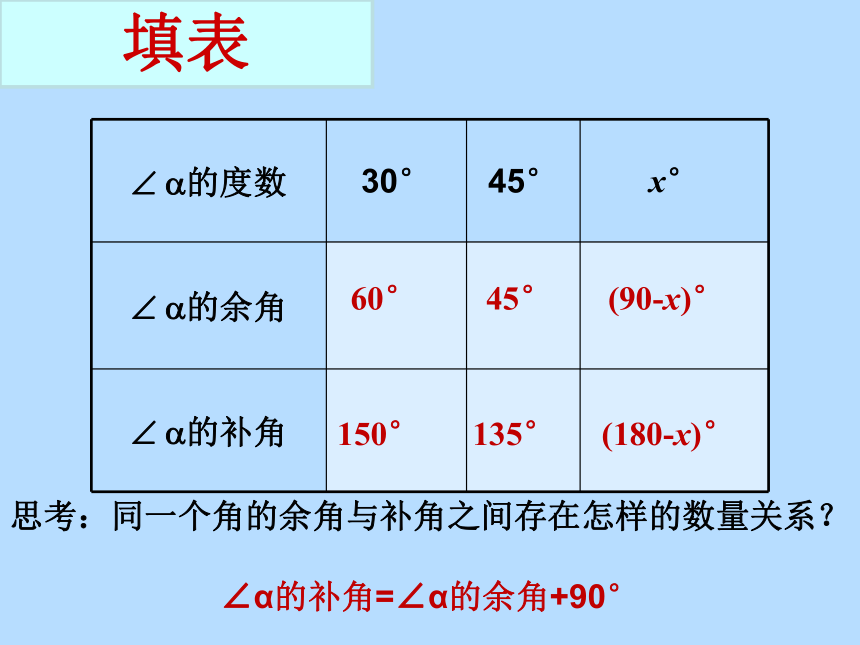
∠ β +∠γ = 180°如果两个角的度数和等于180°(平角),那么这两个角互为补角,简称互补,即其中一个角是另一个角的补角。 概念学习思考:∠ β与∠ γ互补,怎样用等式表示呢?
∠β=180°-∠γ,∠γ=180°-∠β
180°辨析题(2)若∠1+∠2=180°,则∠2是补角.( )(1)如果∠1=35°,∠2=55°,那么两角互余. ( )(3)若∠A+∠B+∠C=180°,则∠A、∠B、∠C
三个角互补.( )× √× ∠2是∠1的补角互余和互补是对两个角而言概念巩固60°150°45°135°(90-x)°(180-x)°填表思考:同一个角的余角与补角之间存在怎样的数量关系?
∠α的补角=∠α的余角+90°例题 已知一个角的补角是这个角的余角的3倍,求这个角的度数.例题分析解: 设这个角的度数为x,根据题意,得
180-x=3(90-x)
解得 x=45
答:这个角为45°.巩固练习 已知一个角的补角比它的余角的2倍大35°,求这个角的度数。
解:设这个角为x度角,根据题意,得
180-x=2(90-x)+35
解得 x=35
答:这个角为35°.
在研究角的度量时,往往需要比度更小的单位,这就是分和秒,把1度的角分成60等份,每一份叫做1分,记作1′;再把1分的角分成60等份,每一份叫做1秒,记作1″ 例如:30°59′ 59 ″ ,读作30度59分59秒 角的度量单位之间的关系是
1°= ___′ 1′=_____″6060角的度量单位例题 已知∠α=53°38′20″,求∠α的余角和补角。例题分析解
∠α的余角=90°-53°38′20″
=89°60′-53°38′20″
=89°59′60″-53°38′20″
=36°21′40″
∠α的补角=180°-53°38′20″
=179°60′-53°38′20″
=179°59′60″- 53°38′20″
=126°21′40″90°=89°59′60″180°=179°59′60″思考:第二题有没有更快捷的求法?
∠α的补角=∠α的余角+90°
巩固练习计算:
(1)77°54′36″+34°27′44″
=111°81′80″
=111°82′20″
=112°22′20″
(2)89°6′4″-24°27′35″
=88°66′4″-24°27′35″
=88°65′64″-24°27′35″
=64°38′29″
1、在下图中,∠AOC、∠BOD都是直角,问:(1)图中有哪几组互余的角?
(2)∠1和∠2有什么数量关系? 同角(或等角)的余角相等 (2)∵∠1和∠3互余 ∵∠2和∠3互余思考 ∴∠1=90°-∠3 ∴∠2=90°-∠3 ∴∠1=∠2(1)∠1与∠3,∠2与∠3∟∟2、在下图中,∠AOB、∠COD都是平角,
问:(1)在∠1、∠2、∠3中有哪几组互补的角?
(2)∠1和∠2有什么数量关系? 同角(或等角)的补角相等 ∵∠1和∠3互补思考 ∵∠2和∠3互补∴∠1=180°-∠3∴∠2=180°-∠3∴∠1=∠2BO3∠1与∠3、∠2与∠3C挑战一下吧!如图,点A、O、B在同一直线上,
∠AOD=∠BOD= COE=90°。(1)图中与?2 互余的角有_________(2)图中与∠3互余的角有_________(3)图中与∠2相等的角有_________(4)图中?2的补角有_____________? 1,?3? 2,?4 ? 4? AOC巩固练习234∟∟∟1、(1)已知∠CAD=50°,以A为顶点,只用三角尺画
出∠CAD的余角B动手操作50°40°40°B’1、(2)已知∠CAD=50°,以A为顶点,只用直尺画出∠CAD的补角E动手操作50°130°130°E’思维拓展 (1)一个角与它的余角相等,这个角是怎样的角?
解:设这个角为x度角,根据题意得
x=90-x
解得 x=45
答:这个角是45°角
(2)一个角与它的补角相等,这个角是怎样的角?
解:设这个角为x度角,根据题意得
x=180-x
解得 x=90
答:这个角是直角(90°的角)
(3)互补的两个角能否都是锐角?能否都是直角?能否都是钝角?
答:这两个角不能都为锐角;
这两个角可以都是直角;
这两个角不能都是钝角。
思维拓展CDENAOBM?1+ ?2=90°?1+ ?2=180°同角(等角)的余角相等同角(等角)的补角相等课堂小结1122作业布置1.练习册习题7.6
2.课课练7.6(1)
∠β=90°-∠α,∠α=90°-∠β
∠ β +∠γ = 180°如果两个角的度数和等于180°(平角),那么这两个角互为补角,简称互补,即其中一个角是另一个角的补角。 概念学习思考:∠ β与∠ γ互补,怎样用等式表示呢?
∠β=180°-∠γ,∠γ=180°-∠β
180°辨析题(2)若∠1+∠2=180°,则∠2是补角.( )(1)如果∠1=35°,∠2=55°,那么两角互余. ( )(3)若∠A+∠B+∠C=180°,则∠A、∠B、∠C
三个角互补.( )× √× ∠2是∠1的补角互余和互补是对两个角而言概念巩固60°150°45°135°(90-x)°(180-x)°填表思考:同一个角的余角与补角之间存在怎样的数量关系?
∠α的补角=∠α的余角+90°例题 已知一个角的补角是这个角的余角的3倍,求这个角的度数.例题分析解: 设这个角的度数为x,根据题意,得
180-x=3(90-x)
解得 x=45
答:这个角为45°.巩固练习 已知一个角的补角比它的余角的2倍大35°,求这个角的度数。
解:设这个角为x度角,根据题意,得
180-x=2(90-x)+35
解得 x=35
答:这个角为35°.
在研究角的度量时,往往需要比度更小的单位,这就是分和秒,把1度的角分成60等份,每一份叫做1分,记作1′;再把1分的角分成60等份,每一份叫做1秒,记作1″ 例如:30°59′ 59 ″ ,读作30度59分59秒 角的度量单位之间的关系是
1°= ___′ 1′=_____″6060角的度量单位例题 已知∠α=53°38′20″,求∠α的余角和补角。例题分析解
∠α的余角=90°-53°38′20″
=89°60′-53°38′20″
=89°59′60″-53°38′20″
=36°21′40″
∠α的补角=180°-53°38′20″
=179°60′-53°38′20″
=179°59′60″- 53°38′20″
=126°21′40″90°=89°59′60″180°=179°59′60″思考:第二题有没有更快捷的求法?
∠α的补角=∠α的余角+90°
巩固练习计算:
(1)77°54′36″+34°27′44″
=111°81′80″
=111°82′20″
=112°22′20″
(2)89°6′4″-24°27′35″
=88°66′4″-24°27′35″
=88°65′64″-24°27′35″
=64°38′29″
1、在下图中,∠AOC、∠BOD都是直角,问:(1)图中有哪几组互余的角?
(2)∠1和∠2有什么数量关系? 同角(或等角)的余角相等 (2)∵∠1和∠3互余 ∵∠2和∠3互余思考 ∴∠1=90°-∠3 ∴∠2=90°-∠3 ∴∠1=∠2(1)∠1与∠3,∠2与∠3∟∟2、在下图中,∠AOB、∠COD都是平角,
问:(1)在∠1、∠2、∠3中有哪几组互补的角?
(2)∠1和∠2有什么数量关系? 同角(或等角)的补角相等 ∵∠1和∠3互补思考 ∵∠2和∠3互补∴∠1=180°-∠3∴∠2=180°-∠3∴∠1=∠2BO3∠1与∠3、∠2与∠3C挑战一下吧!如图,点A、O、B在同一直线上,
∠AOD=∠BOD= COE=90°。(1)图中与?2 互余的角有_________(2)图中与∠3互余的角有_________(3)图中与∠2相等的角有_________(4)图中?2的补角有_____________? 1,?3? 2,?4 ? 4? AOC巩固练习234∟∟∟1、(1)已知∠CAD=50°,以A为顶点,只用三角尺画
出∠CAD的余角B动手操作50°40°40°B’1、(2)已知∠CAD=50°,以A为顶点,只用直尺画出∠CAD的补角E动手操作50°130°130°E’思维拓展 (1)一个角与它的余角相等,这个角是怎样的角?
解:设这个角为x度角,根据题意得
x=90-x
解得 x=45
答:这个角是45°角
(2)一个角与它的补角相等,这个角是怎样的角?
解:设这个角为x度角,根据题意得
x=180-x
解得 x=90
答:这个角是直角(90°的角)
(3)互补的两个角能否都是锐角?能否都是直角?能否都是钝角?
答:这两个角不能都为锐角;
这两个角可以都是直角;
这两个角不能都是钝角。
思维拓展CDENAOBM?1+ ?2=90°?1+ ?2=180°同角(等角)的余角相等同角(等角)的补角相等课堂小结1122作业布置1.练习册习题7.6
2.课课练7.6(1)
