第4节 长方体中棱与平面位置关系的认识(1) 课件(13张PPT)
文档属性
| 名称 | 第4节 长方体中棱与平面位置关系的认识(1) 课件(13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 00:00:00 | ||
图片预览



文档简介
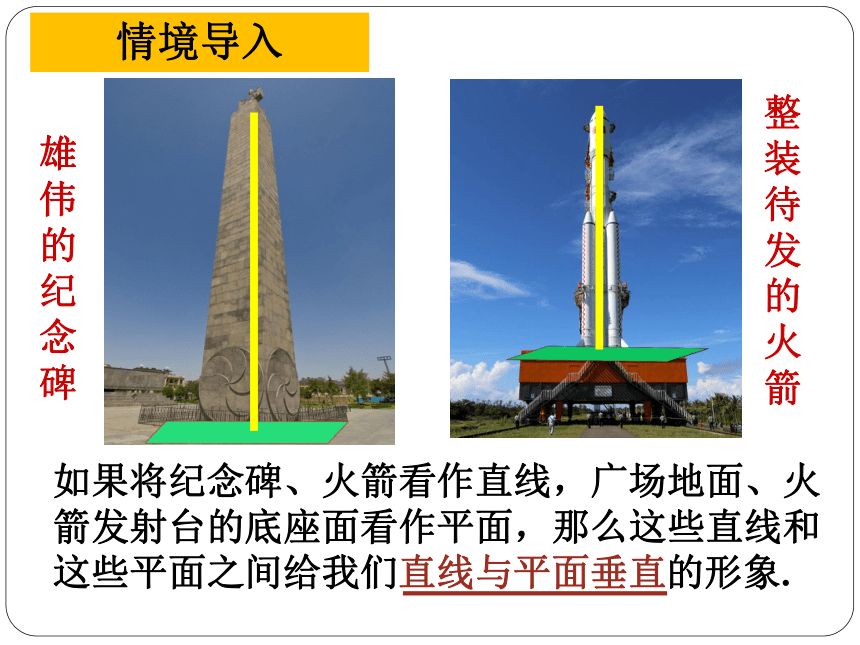
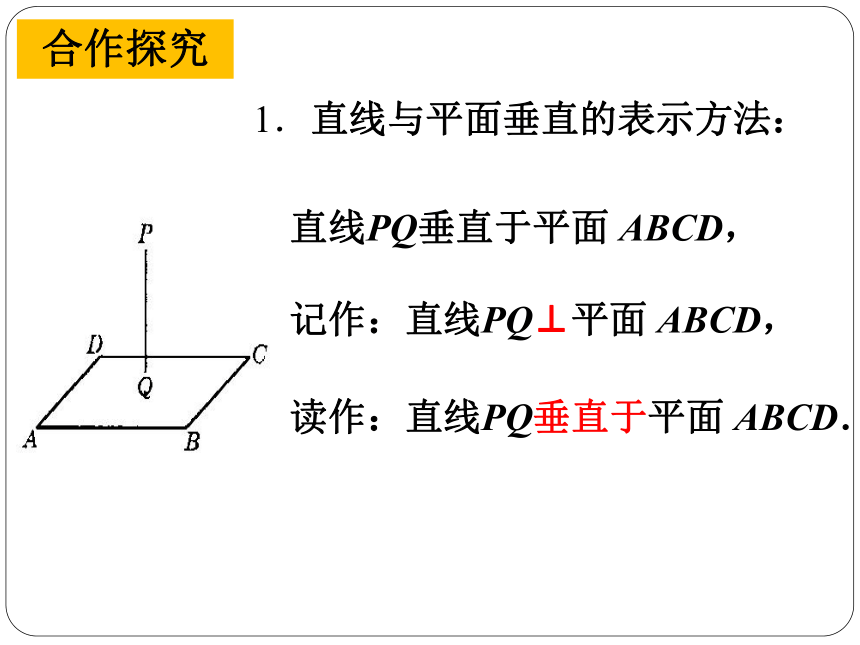
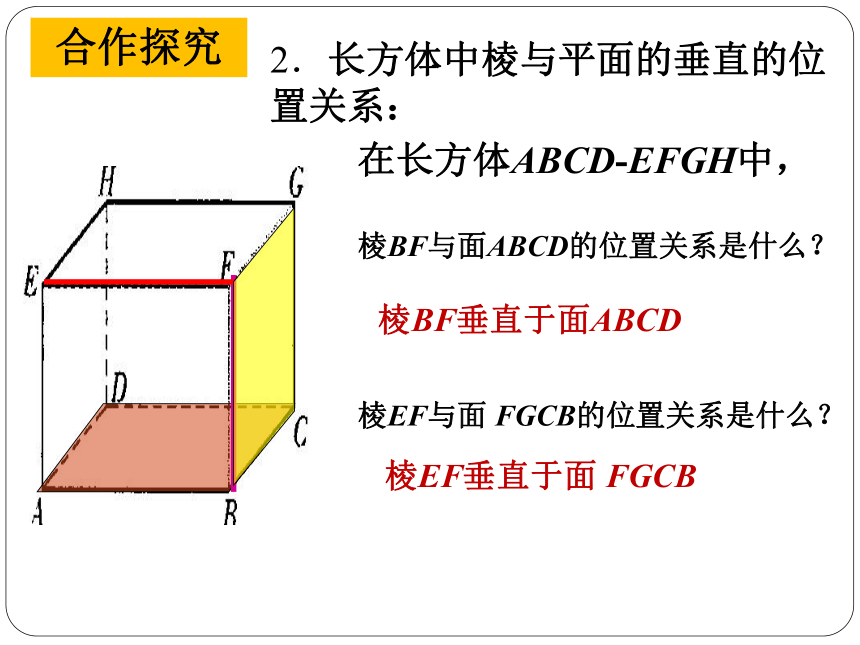
课件13张PPT。§8.4长方体中棱与平面位置关系的认识(1)1.如图,在长方体ABCD-EFGH中,棱BF与面ABCD,棱EF与面 FGCB的位置关系是什么? 情境导入棱BF垂直于面ABCD棱EF垂直于面 FGCB情境导入 如果将纪念碑、火箭看作直线,广场地面、火箭发射台的底座面看作平面,那么这些直线和这些平面之间给我们 的形象.雄伟的纪念碑整装待发的火箭直线与平面垂直合作探究 1.直线与平面垂直的表示方法:直线PQ垂直于平面 ABCD,记作:直线PQ⊥平面 ABCD,读作:直线PQ垂直于平面 ABCD. 合作探究 2.生活中直线与平面垂直的例子在长方体ABCD-EFGH中,棱BF与面ABCD的位置关系是什么? 棱EF与面 FGCB的位置关系是什么? 2.长方体中棱与平面的垂直的位置关系:合作探究 棱BF垂直于面ABCD棱EF垂直于面 FGCB3.直线与平面垂直的检验方法: 只能用于检验直线是否垂直于水平面.〖 “铅垂线”检验法〗若铅垂线能紧贴待检验的直线,那么该直线垂直于水平面.合作探究 3.直线与平面垂直的检验方法: 可以检验一般的直线与平面是否垂直.〖 “三角尺”检验法〗利用三角尺的直角,如果两把三角尺各有一条直角边紧贴平面且位置相交,另一直角边都能与直线紧贴,那么该直线与这个平面垂直.合作探究 3.直线与平面垂直的检验方法: 〖 “合页型折纸”检验法〗将合页型折纸直立于桌面,如果折痕能紧贴细棒,那么细棒垂直于桌面.合作探究 思考:“三角尺”检验法与“合页型折纸”检验方法有什么相同之处? 例1 在长方体ABCD-EFGH中,⑴与棱DC垂直的平面有哪些?⑵与面DCGH垂直的棱有哪几条?与棱DC垂直的平面有平面ADHE与面DCGH垂直的棱有四条,分别是棱EH、FG、AD、BC.和平面BCGF.在长方体中与一条棱垂直的平面有两个.在长方体中与一个面垂直的棱有四条.合作探究 1、请根据左图说明棱BF与平面 ABCD垂直的理由. 2、请根据左图说明AE与平面 ABCD垂直的理由.课堂练习课堂小结 2.直线与平面的垂直的检验方法:“铅垂线”检验法、“三角尺”检验法、“合页型折纸”检验法.3.在长方体中与一条棱垂直的面有两个,与一个面垂直的棱有四条.
1.直线与平面的垂直关系及表示方法.
1.直线与平面的垂直关系及表示方法.
