北京课改版九年级数学上册第21章 《圆(上)》 期末复习卷(含答案)
文档属性
| 名称 | 北京课改版九年级数学上册第21章 《圆(上)》 期末复习卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 368.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-07 23:26:59 | ||
图片预览



文档简介
北京版九年级数学上册
第21章 圆(上)
期末复习卷
(时间90分钟,满分120分)
一.选择题(本大题共10小题,每小题3分,共30分)
1.如图1,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.3
2.如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )
3. 一个圆锥的侧面展开图是圆心角为120°且半径为6的扇形,则这个圆锥的底面半径为( )
A.2 B.2 C.2.5 D.3
4.如图3,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为( )
A.30° B.35° C.40° D.45°
5.如图,⊙O的半径为5,AB为弦,半径OC⊥AB,垂足为点E,若OE=3,则AB的长是( )
A.4 B.6
C.8 D.10
6.如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的弧EF上时,弧BC的长度等于( )
A. B.
C. D.
7. 一个滑轮起重装置如图所示,滑轮的半径是15 cm,当重物上升15 cm时,滑轮的一条半径OA绕轴心O按顺时针方向旋转的角度约为(π取3.14,结果精确到1°)( )
A.115° B.60°
C.57° D.29°
8.一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )
A.4 B.6
C.8 D.9
9.若四边形ABCD是⊙O的内接四边形,且∠A∶∠B∶∠C=1∶3∶8,则∠D的度数是( )
A.10° B.30°
C.80° D.120°
10.如图,将△ABC绕点C顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )
A.π B.π
C.6π D.π
二.填空题(共8小题,3*8=24)
11.如图,CD是⊙O的直径,若AB⊥CD,垂足为B,∠OAB=40°,则∠C等于__ __度.
12.圆心角为60°,半径为4 cm的扇形的弧长为__ __cm.
13.如图,△ABC是⊙O的内接三角形,点D是的中点.已知∠AOB=98°,∠COB=120°,则∠ABD的度数为__ __.
14.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=15°,AB=6 cm,则⊙O半径为__ __cm.
15.已知⊙O的半径OA=6,以点A为圆心,OA为半径的弧交⊙O于B、C两点,则BC= .
16.如图,四边形ABCD是⊙O的内接四边形,点E在AB的延长线上,BF是∠CBE的平分线,∠ADC=110°,则∠FBE=__ __ .
17. 如图,△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中,,,,圆心依次按A,B,C…循环,它们依次相连结.若AB=1,则曲线CDEF的长是__ __(结果保留π).
18.如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是 .
三.解答题(共7小题,66分)
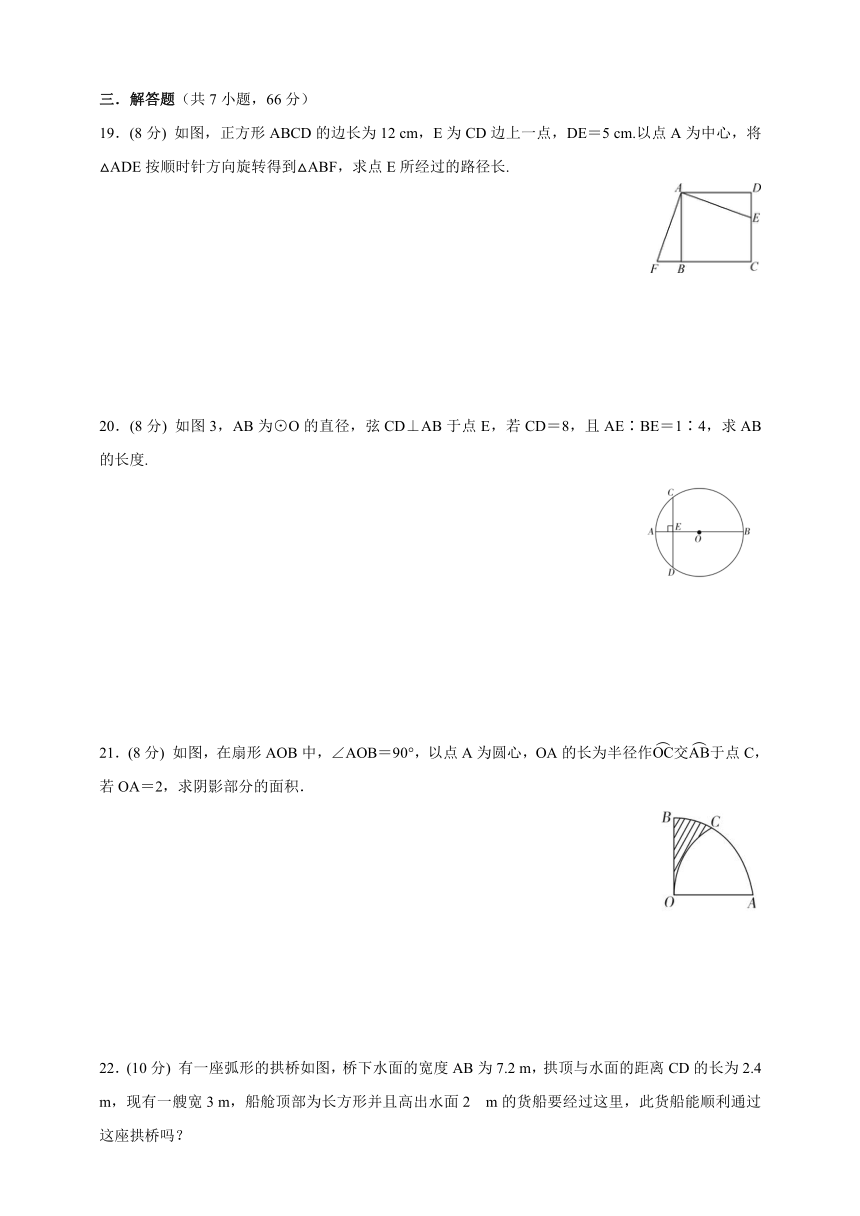
19.(8分) 如图,正方形ABCD的边长为12 cm,E为CD边上一点,DE=5 cm.以点A为中心,将△ADE按顺时针方向旋转得到△ABF,求点E所经过的路径长.
20.(8分) 如图3,AB为⊙O的直径,弦CD⊥AB于点E,若CD=8,且AE∶BE=1∶4,求AB的长度.
21.(8分) 如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作交于点C,若OA=2,求阴影部分的面积.
22.(10分) 有一座弧形的拱桥如图,桥下水面的宽度AB为7.2 m,拱顶与水面的距离CD的长为2.4 m,现有一艘宽3 m,船舱顶部为长方形并且高出水面2 m的货船要经过这里,此货船能顺利通过这座拱桥吗?
23.(10分) 如图,正方形ABCD内接于⊙O,其边长为4,求⊙O的内接正三角形EFG的边长.
24.(10分) 如图,已知Rt△ABD中,∠A=90°,将斜边BD绕点B顺时针方向旋转至BC,使BC∥AD,过点C作CE⊥BD于点E.
(1)求证:△ABD≌△ECB;
(2)若∠ABD=30°,BE=3,求的长.
25.(12分) 如图所示,⊙O是△ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交⊙O于点D,连结BD、DC.
(1)求证:BD=DC=DI;
(2)若⊙O的半径为10,∠BAC=120°,求△BDC的面积.
参考答案:
1-5BABDC 6-10BCDDD
11. 25
12. π
13. 101°
14. 6
15. 6
16. 55°
17. 4π
18. 6π-9
19. 解: ∵AD=12 cm,DE=5 cm,
∴AE==13(cm).
∵将△ADE按顺时针方向旋转得到△ABF,AD⊥AB,
∴旋转角为∠DAB=90°,
∴点E所经过的路径长为=(cm).
20. 解: 如图,连结OC,设AE=x,
∵AE∶BE=1∶4,∴BE=4x,∴OC=2.5x,∴OE=1.5x,
∵CD⊥AB,∴CE=DE=CD=4,
在Rt△OCE中,OE2+CE2=OC2,
∴(1.5x)2+42=(2.5x)2,
解得:∴x=2,∴AB=2OC=5x =10.
21. 解:如图,连结OC,AC,△OAC是等边三角形,扇形OBC的圆心角是30°,
阴影部分的面积等于扇形OBC的面积减去弓形OC的面积.
S扇形OBC==π,
S弓形OC=-×22=π-,
∴S阴影=π-=-π.
22. 解:如答图,连结ON,OB.
∵OC⊥AB,∴D为AB中点,
∵AB=7.2 m,∴BD=AB=3.6 m.
又∵CD=2.4 m,
∴设OB=OC=ON=r,则OD=(r-2.4)m.
在Rt△BOD中,由勾股定理得r2=(r-2.4)2+3.62,解得r=3.9.
∵CD=2.4 m,船舱顶部为长方形并高出水面2 m,∴CE=2.4-2=0.4(m),
∴OE=r-CE=3.9-0.4=3.5(m),
在Rt△OEN中,EN2=ON2-OE2=3.92-3.52=2.96(m2),∴EN≈1.72(m).
∴MN=2EN=2×1.72=3.44 m>3,
∴此货船能顺利通过这座弧形拱桥.
23. 解:如图,连结AC,OE,OF,过点O作OM⊥EF于点M.
∵四边形ABCD是正方形,
∴AB=BC=4,∠ABC=90°,
∴AC是直径,AC=4,
∴OE=OF=2,
∵OM⊥EF,
∴EM=MF,
∵△EFG是等边三角形,
∴∠GEF=60°,
∵在Rt△OME中,OE=2,∠OEM=∠GEF=30°,
∴OM=,EM=OM=,
∴EF=2.
24. (1)证明:∵∠A=90°,CE⊥BD,
∴∠A=∠BEC=90°.
∵BC∥AD,∴∠ADB=∠EBC.
∵将斜边BD绕点B顺时针方向旋转至BC,
∴BD=BC.在△ABD和△ECB中,
∴△ABD≌△ECB;
(2)∵△ABD≌△ECB,∴AD=BE=3.
∵∠A=90°,∠ABD=30°,∴BD=2AD=6,
∵BC∥AD,∴∠A+∠ABC=180°,
∴∠ABC=90°,∴∠DBC=60°,
∴的长为=2π.
25. (1)证明:∵AD平分∠BAC,∴∠BAD=∠DAC,
∴=,∴BD=DC.
∵BI平分∠ABC,∴∠ABI=∠CBI.
∵∠BAD=∠DAC,∠DBC=∠DAC,∴∠BAD=∠DBC.
又∵∠DBI=∠DBC+∠CBI,∠DIB=∠ABI+∠BAD,
∴∠DBI=∠DIB,∴BD=ID,∴BD=DC=DI.
(2)解:∵∠BAC=120°,四边形ABDC为圆内接四边形,∴∠BDC=60°.
∵BD=DC,∴△BDC为等边三角形.
连结CO并延长交BD于点E,则OE⊥BD,连结OB、OD,∴BE=BD.
又∵OB=10,OE=OC=5,∴BE==5,
∴BD=2BE=10.
又∵CE=OE+OC=15,
∴S△BDC=BD·CE=×10×15=75.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
