13.1 邻补角、对顶角 课件(13张)
文档属性
| 名称 | 13.1 邻补角、对顶角 课件(13张) |

|
|
| 格式 | zip | ||
| 文件大小 | 140.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 00:00:00 | ||
图片预览


文档简介
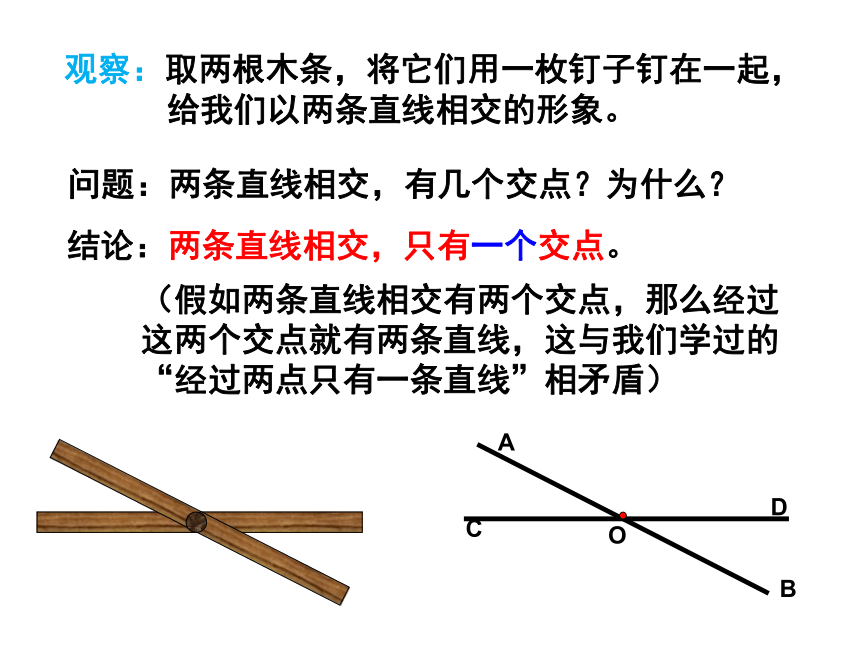
课件13张PPT。第十三章 相交线 平行线13.1 邻补角、对顶角观察:取两根木条,将它们用一枚钉子钉在一起,
给我们以两条直线相交的形象。问题:两条直线相交,有几个交点?为什么?结论:两条直线相交,只有一个交点。ABCDO(假如两条直线相交有两个交点,那么经过
这两个交点就有两条直线,这与我们学过的
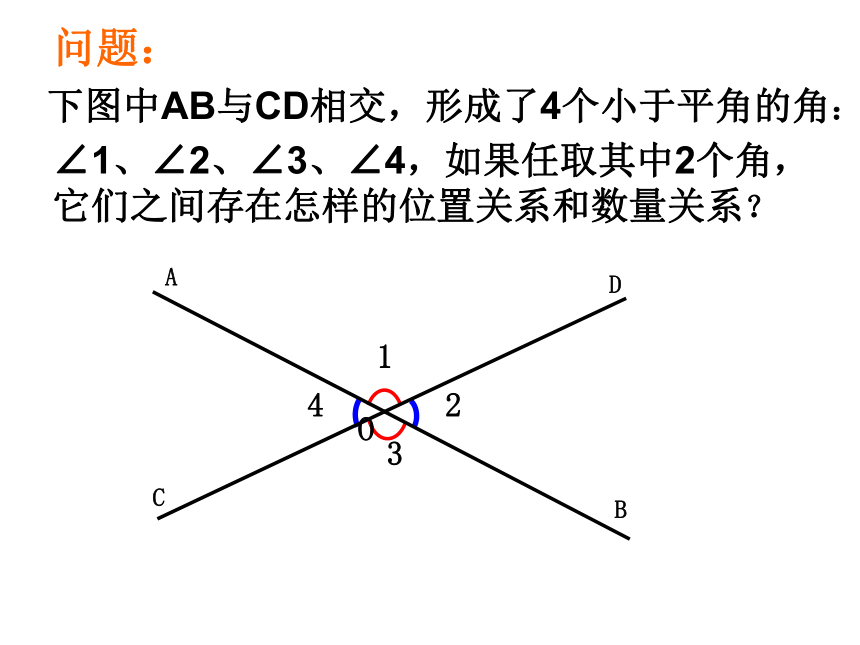
“经过两点只有一条直线”相矛盾)下图中AB与CD相交,形成了4个小于平角的角:问题:∠1、∠2、∠3、∠4,如果任取其中2个角,它们之间存在怎样的位置关系和数量关系? 1.邻补角的概念:
如图:∠1与∠2有一条公共边OD,它们的另外一条
边为OA、OB互为反向延长线,具有这种关系的两个角
叫做互为邻补角。找一找:图中还有没有其他邻补角,如果有,是哪些角?分别为:∠1与∠2,∠2与∠3,
∠3与∠4,∠1与∠4。
问题1:它们在数量上有什么关系?(相加=180°)问题2:互为邻补角与互为补角有什么区别与联系?“互为邻补角”包括两角之间的位置关系和数量关系两个方面的要求,而“互为补角”仅指两角之间的数量关系。 ∠1与∠3 有公共顶点O,而没有公共边,其中∠1的
两边OA、OD是∠3的两边OB、OC的反向延长线,
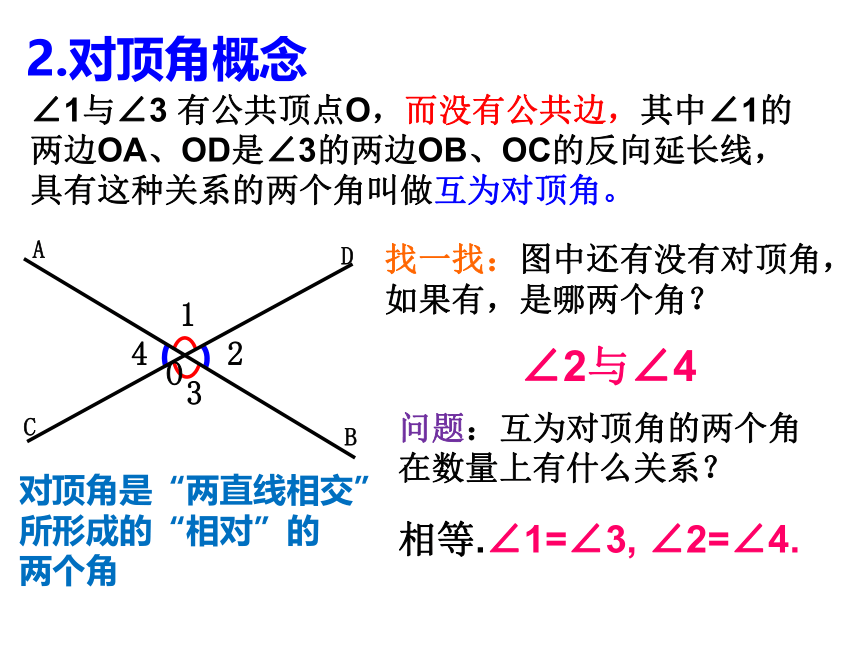
具有这种关系的两个角叫做互为对顶角。找一找:图中还有没有对顶角,如果有,是哪两个角?∠2与∠42.对顶角概念问题:互为对顶角的两个角在数量上有什么关系?相等.∠1=∠3, ∠2=∠4.对顶角是“两直线相交”
所形成的“相对”的
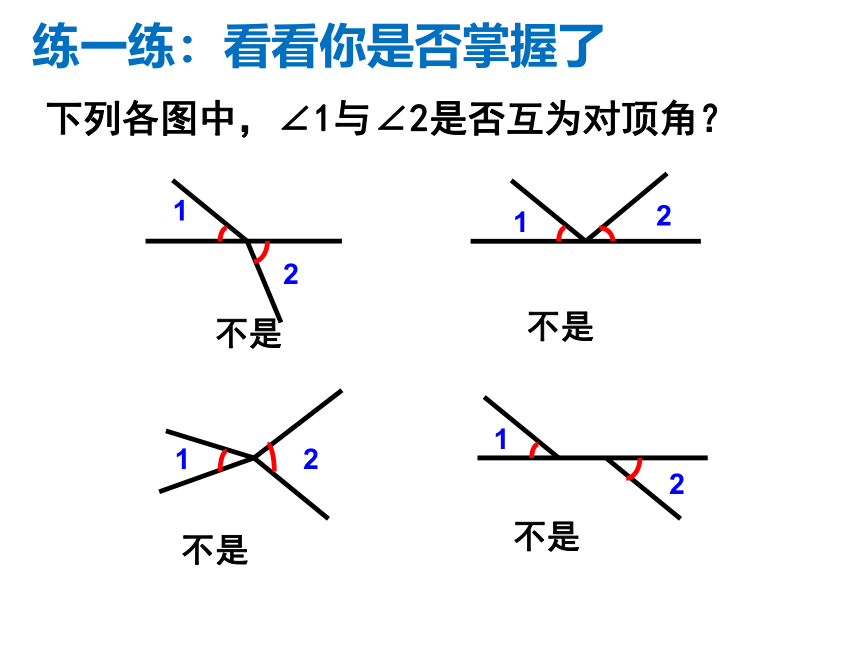
两个角 下列各图中,∠1与∠2是否互为对顶角?12121212不是不是不是不是练一练:看看你是否掌握了3、对顶角的性质:对顶角相等.因为∠1与∠2、 ∠2与∠3分别是邻补角(已知),
所以∠1+ ∠2=180°,∠2+ ∠3=180°(邻补角的意义),
得∠1+ ∠2= ∠2+ ∠3(等量代换).
所以∠1=∠3(等量减等量,差相等).
类似的,可以说明∠2= ∠4.
这样,我们得到了对顶角的性质.例题1 如图,直线AB,CD相交于点O,∠BOE=90°,
(1)图中的对顶角是_______________________;
(2)∠1的邻补角是______________________;
(3)∠2的余角是___________________.ABDEC12∠AOD与∠BOC, ∠AOC与∠1∠AOD与∠BOC∠AOC与∠1O例题讲解:例题2如图,已知直线AB、CD相交于点O,∠AOC=50°,
求∠BOD、∠AOD、∠BOC的度数。 解:因为直线AB、CD相交于点O,所以∠BOD与∠AOC是对顶角,得:
∠BOD =∠AOC=50°
因为直线AB、CD相交于点O,
所以∠AOD与∠AOC是邻补角,得
∠AOD =180°-∠AOC
=180°-50°
=130°
因为∠BOC与∠AOD是对顶角,得:
∠BOC =∠AOD=130° 如图,直线AB、CD相交于点O,OE平分∠BOC.
已知∠BOE=65°,求∠AOD、∠AOC的度数. 解:因为OE平分∠BOC,
所以∠BOC=2∠BOE=130°
因为直线AB、CD相交于点O,
所以∠BOC与∠AOD是对顶角,
所以∠AOD=∠BOC=130°
而∠BOC与∠AOC是邻补角,
所以∠AOC =180°-∠BOC
=180°-130°
=50° 例题3巩固练习:P41书后练习2、3 补充练习:1:已知一个角的补角是这个角的余角的四倍,
求这个角的度数。课堂小结 :①两条直线相交而成的角
②有一个公共顶点
③没有公共边①两条直线相交而成的角
②有一个公共顶点
③有一条公共边邻补角互补对顶角相等都是两直线相交而成的角,都有一个公共顶点,它们都是成对出现。对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个角的对顶角有一个,而一个角的邻补角有两个。作业:(1)练习册
给我们以两条直线相交的形象。问题:两条直线相交,有几个交点?为什么?结论:两条直线相交,只有一个交点。ABCDO(假如两条直线相交有两个交点,那么经过
这两个交点就有两条直线,这与我们学过的
“经过两点只有一条直线”相矛盾)下图中AB与CD相交,形成了4个小于平角的角:问题:∠1、∠2、∠3、∠4,如果任取其中2个角,它们之间存在怎样的位置关系和数量关系? 1.邻补角的概念:
如图:∠1与∠2有一条公共边OD,它们的另外一条
边为OA、OB互为反向延长线,具有这种关系的两个角
叫做互为邻补角。找一找:图中还有没有其他邻补角,如果有,是哪些角?分别为:∠1与∠2,∠2与∠3,
∠3与∠4,∠1与∠4。
问题1:它们在数量上有什么关系?(相加=180°)问题2:互为邻补角与互为补角有什么区别与联系?“互为邻补角”包括两角之间的位置关系和数量关系两个方面的要求,而“互为补角”仅指两角之间的数量关系。 ∠1与∠3 有公共顶点O,而没有公共边,其中∠1的
两边OA、OD是∠3的两边OB、OC的反向延长线,
具有这种关系的两个角叫做互为对顶角。找一找:图中还有没有对顶角,如果有,是哪两个角?∠2与∠42.对顶角概念问题:互为对顶角的两个角在数量上有什么关系?相等.∠1=∠3, ∠2=∠4.对顶角是“两直线相交”
所形成的“相对”的
两个角 下列各图中,∠1与∠2是否互为对顶角?12121212不是不是不是不是练一练:看看你是否掌握了3、对顶角的性质:对顶角相等.因为∠1与∠2、 ∠2与∠3分别是邻补角(已知),
所以∠1+ ∠2=180°,∠2+ ∠3=180°(邻补角的意义),
得∠1+ ∠2= ∠2+ ∠3(等量代换).
所以∠1=∠3(等量减等量,差相等).
类似的,可以说明∠2= ∠4.
这样,我们得到了对顶角的性质.例题1 如图,直线AB,CD相交于点O,∠BOE=90°,
(1)图中的对顶角是_______________________;
(2)∠1的邻补角是______________________;
(3)∠2的余角是___________________.ABDEC12∠AOD与∠BOC, ∠AOC与∠1∠AOD与∠BOC∠AOC与∠1O例题讲解:例题2如图,已知直线AB、CD相交于点O,∠AOC=50°,
求∠BOD、∠AOD、∠BOC的度数。 解:因为直线AB、CD相交于点O,所以∠BOD与∠AOC是对顶角,得:
∠BOD =∠AOC=50°
因为直线AB、CD相交于点O,
所以∠AOD与∠AOC是邻补角,得
∠AOD =180°-∠AOC
=180°-50°
=130°
因为∠BOC与∠AOD是对顶角,得:
∠BOC =∠AOD=130° 如图,直线AB、CD相交于点O,OE平分∠BOC.
已知∠BOE=65°,求∠AOD、∠AOC的度数. 解:因为OE平分∠BOC,
所以∠BOC=2∠BOE=130°
因为直线AB、CD相交于点O,
所以∠BOC与∠AOD是对顶角,
所以∠AOD=∠BOC=130°
而∠BOC与∠AOC是邻补角,
所以∠AOC =180°-∠BOC
=180°-130°
=50° 例题3巩固练习:P41书后练习2、3 补充练习:1:已知一个角的补角是这个角的余角的四倍,
求这个角的度数。课堂小结 :①两条直线相交而成的角
②有一个公共顶点
③没有公共边①两条直线相交而成的角
②有一个公共顶点
③有一条公共边邻补角互补对顶角相等都是两直线相交而成的角,都有一个公共顶点,它们都是成对出现。对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个角的对顶角有一个,而一个角的邻补角有两个。作业:(1)练习册
