人教版八年级上册14.2.2完全平方公式课件(共40张PPT)
文档属性
| 名称 | 人教版八年级上册14.2.2完全平方公式课件(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 860.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-08 00:00:00 | ||
图片预览











文档简介
(共40张PPT)
14.2.2 完全平方公式
1.掌握完全平方公式的特征,能运用公式进行计算。
2.熟悉完全平方公式的常用变形,并且熟练应用变形解题。
3.掌握添括号法则,能正确添加括号。
学习目标
重点:完全平方公式的灵活应用应用.
难点:添括号法则
问题引入1
某学校对操场进行改造,原来操场是一个边长为a的正方形,现要扩建成一个边长比原来大b的正方形操场,那么能用两种不同的方法表示大正方形的面积吗?
b
a
b
a
①
+
+
完全平方和公式:
(x+y)2=x2+y2
?
问题引入1
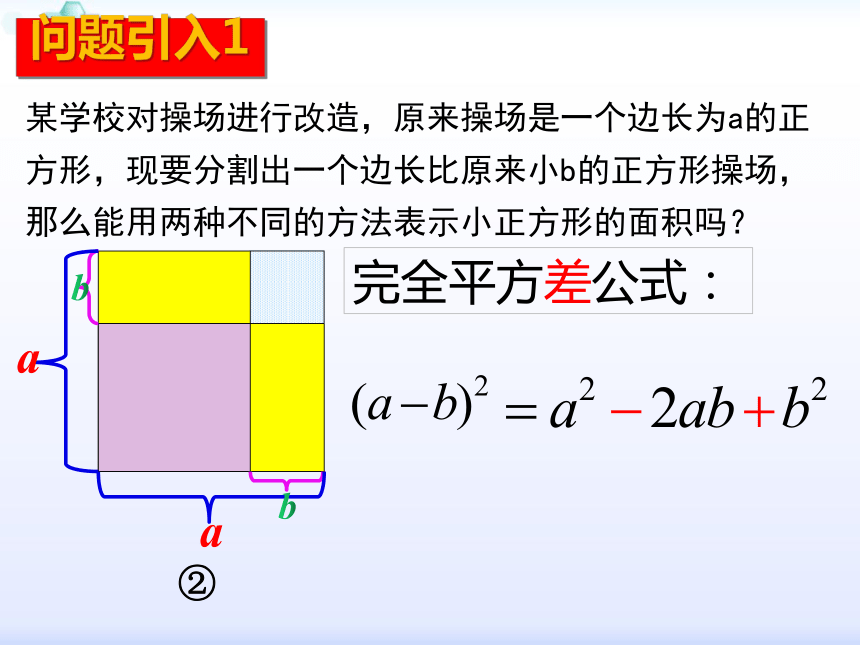
某学校对操场进行改造,原来操场是一个边长为a的正方形,现要分割出一个边长比原来小b的正方形操场,那么能用两种不同的方法表示小正方形的面积吗?
b
a
b
a
②
完全平方差公式:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(乘法的)完全平方公式:
知识点一:完全平方公式
新知归纳
首平方,尾平方,
积的二倍放中央.
口答:(1)(p+1)2
(2)(m+2)2
(3)(P-1)2
(4)(m-2)2
归纳总结
公式特点:
4、公式中的字母a,b可以表示数,单项式和多项式.
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中间的符号相同.
首平方,尾平方,
积的二倍放中央.
练习.计算:(口答):
(1) (4m+n)2
(2) (a-b)2
(3)(-y-x)2
(4)(1-x)2
=16m2+8mn+n2
=a2-2ab+b2
=y2+2xy+x2
=1-2x+x2
练习.计算:(口答):
(5) (x+y)2
(6) (5a+b)2
(7)(3a-b)2
(8)(m-2n)2
=x2+2xy+y2
=25a2+10ab+b2
=9a2-6ab+b2
=m2-4mn+4n2
典例讲评
例1:运用完全平方公式计算:
(1)(4m+n)2
例2:运用完全平方公式计算:
(1)1022 (2)992
当堂训练
思考:(a+b)2与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
(a-b)2与a2-b2相等吗?为什么?
请尝试用多种方法求解上述例题。
当堂训练
拓展练习:
1. =_______;
2.若 是一个完全平方公式,
则 _______;
3.若 是一个完全平方公式,
则 _______;
1
4.请添加一项________,使得 是完全平方式.
知识点二:完全平方公式的常用变形
(1)a2+b2=(a+b)2-2ab=(a-b)2+2ab
完全平方公式的常见变形
一题多变:已知a-b=13,ab=-12,求下列各式的值:
知识点二:完全平方公式的常用变形
完全平方公式的常见变形
(2)(a+b)2+(a-b)2=2a2+2b2
知识点二:完全平方公式的常用变形
完全平方公式的常见变形
(3)(a+b)2-(a-b)2=4ab
(4)ab= [(a+b)2-(a2+b2)]=
知识点二:完全平方公式的常用变形
完全平方公式的常见变形
知识点二:完全平方公式的常用变形
(1)a2+b2=(a+b)2-2ab=(a-b)2+2ab
完全平方公式的常见变形
知识点三:添括号法则
我们学过去括号法则,即
口诀:去括号,看符号;
是“+”号,不变号;
是“-”号,全变号.
运用乘法公式计算,有时要在式子中添括号.把上面等式左右两边交换位置就得到:
a + b + c=a + (b+c)
a﹣b﹣c=a﹣(b+c)
a + (b+c)=a + b + c
a﹣(b+c)=a﹣b﹣c
知识点三:添括号法则
新知探究
填空:
(1)a+(b-c) = ;(2)a-(b-c)= ;
(3) a-(b+c)= ;(4)a-(-b-c)= .
根据上面四个等式填空:
(1)a+b-c=a+( ) (2) a-b+c=a-( )
(3)a-b-c=a-( ) (4) a+b+c=a-( )
观察这四个等式的左右两边,你发现了什么?
b-c
b-c
b+c
-b-c
a+b-c
a-b+c
a-b-c
a+b+c
新知归纳
知识点三:添括号法则
a + b – c = a + ( b – c)
a + b – c = a – ( – b +c )
符号均没有变化
符号均发生了变化
添上“+ ( )”, 括号里的各项都不变符号.
添上“– ( )”, 括号里的各项都改变符号.
口诀:
添括号,看符号;
添“+”号,不变号;
添“-”号,全变号.
新知归纳
知识点三:添括号法则
口诀:添括号,看符号;
添“+”号,不变号;
添“-”号,全变号.
添括号法则
添括号时,如果括号前面是“+”号,括到括号里的各项都不改变符号;
如果括号前面是“-”号,括到括号里的各项都要改变符号;
当堂训练
当堂训练
当堂训练
1.不改变代数式a2﹣(2a+b+c)的值,把它括号前面的符号变为相反的符号,应为( )
A.a2+(-2a+b+c) B.a2+(-2a-b-c)
C.a2+(-2a)+b+c D.a2-(-2a-b-c)
2.将多项式3x3-2x2+4x-5添括号后正确的是( )
A.3x3-(2x2+4x-5) B.(3x3+4x)-(2x2+5)
C.(3x3-5)+(﹣2x2-4x) D.2x2+(3x3+4x-5)
B
B
当堂检测
3.在下列各式的括号内填上适当的项.
(1)x3-3x2y+3xy2﹣y3=x3+( );
(2)2﹣x2+2xy﹣y2=2﹣( );
4.下列添括号错误的是( )
A.a2ーb2ーb+a=a2ーb2+(a-b)
B.(a+b+c)(aーbーc)=[a+(b+c)][a-(b+c)]
C.a﹣b+c﹣d=(a﹣d)+(c﹣b)
D.aーb=ー(b+a)
x2﹣2xy+y2
-3x2y+3xy2﹣y3
D
归纳总结
(1)在使用添括号法则时,要明确括到括号里的是哪些项,括号前面的符号是正号还是负号;
(2)添括号与去括号是互逆的,符号的变化是一致的,在运用添括号法则时,可与去括号法则相比较.注意不要只改变括号内部分项的符号;
(3)添括号比去括号容易出错,特别是当括号前添“﹣”号时,添括号后是否正确,可利用去括号法则检验.
null
典例讲评
null
当堂训练
利用乘法公式计算:
(1) (x+y+2)(x+y-2) ;(2) (a-b+c)(a+b-c).
null
当堂训练
达标检测
1.下列计算正确的是( )
A.(x+y)2=x2+y2 B.(x-y)2=x2-2xy-y2
C.(x+2y)(x-2y)=x2-2y2 D.(-x+y)2=x2-2xy+y2
2下列各式,计算结果是 m2n2 -m+1的是( )
A .(mn- )2 B. ( mn+1)2
C. ( mn-1)2 D. ( mn-1)2
3若(x-y)2=(x+y)2+( ),则括号中应填的是( )
A.-2xy B. 2xy C. -4xy D. 4xy
C
D
1
4
C
达标检测
4.将面积为a2的正方形边长均增加2,则正方形的面积增加了( )
A.4 B.2a+4 C.4a+4 D. 4a
5(易错题)计算:(3x-2y)2= ,
(-2t- )2= ,
C
9x2-12xy+4y2
达标检测
运用完全平方公式计算:
(1)1022 (2)992
解:(1) 1022 = (100+2)2= 1002+2×100×2+22
= 10000+400+4
= 10404
(2)992 = (100-1)2 =1002-2×100×1+12
= 10000-200+1
= 9801
达标检测
1.若(y+a)2=y2-6y+b,则a,b的值分别为( )
A.a=3,b=9 B.a= -3,b= -9
C.a=3,b= -9 D,a= -3,b=9
2.下列运算中,错误的有( )
①(2x+y)2=4x2+y2; ②(a-3b)2=a2-9b2 ;
③(-x-y)2=x2-2xy+y2; ④(x- )2=x2-x+
A.1个 B.2个 C.3个 D.4个
D
C
达标检测
3.( -3)2=16a2- + .
4.已知2x+y=1,则代数式(y+1)2-(y2-4x)的值为 .
5.如果y2-ky+9是完全平方式,则 k= .
6.利用完全平方公式计算:
(1)2012 (2)1992
3
4a
24ab
9b2
达标检测
2
null
达标检测
1.应用平方差公式计算(x+2y﹣1)(x﹣2y+1),则下列变形正确的是( )
A.[x﹣(2y+1)]2
B.[x+(2y+1)]2,
C.[x+(2y﹣1)][x﹣(2y﹣1)]
D.[(x﹣2y)+1][(x﹣2y)﹣1]
C
C
达标检测
2.下列式子中不能用乘法公式计算的是( )
A.(a+b﹣c)(a﹣b+c)
B.(a﹣b﹣c)2
C.(2a+b+2)(a﹣2b﹣2)
D.(2a+3b﹣1)(1﹣2a﹣3b).
C
null
达标检测
3.计算(a+1)2(a-1)2的结果是( )
A.a4-1 B.a4+1 C.a4+2a2+1 D.a4-2a2+1
4.利用乘法公式计算:
(1) (x+2y﹣3)(x﹣2y+3) ;(2) (a+b+c)2.
D
null
达标检测
5.利用乘法公式计算(变式练习):
(1) (3a+b﹣2)(3a﹣b+2) ;(2) (a+b﹣c)2;
(3) (2x+3y﹣1)(1+2x+3y)
14.2.2 完全平方公式
1.掌握完全平方公式的特征,能运用公式进行计算。
2.熟悉完全平方公式的常用变形,并且熟练应用变形解题。
3.掌握添括号法则,能正确添加括号。
学习目标
重点:完全平方公式的灵活应用应用.
难点:添括号法则
问题引入1
某学校对操场进行改造,原来操场是一个边长为a的正方形,现要扩建成一个边长比原来大b的正方形操场,那么能用两种不同的方法表示大正方形的面积吗?
b
a
b
a
①
+
+
完全平方和公式:
(x+y)2=x2+y2
?
问题引入1
某学校对操场进行改造,原来操场是一个边长为a的正方形,现要分割出一个边长比原来小b的正方形操场,那么能用两种不同的方法表示小正方形的面积吗?
b
a
b
a
②
完全平方差公式:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(乘法的)完全平方公式:
知识点一:完全平方公式
新知归纳
首平方,尾平方,
积的二倍放中央.
口答:(1)(p+1)2
(2)(m+2)2
(3)(P-1)2
(4)(m-2)2
归纳总结
公式特点:
4、公式中的字母a,b可以表示数,单项式和多项式.
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中间的符号相同.
首平方,尾平方,
积的二倍放中央.
练习.计算:(口答):
(1) (4m+n)2
(2) (a-b)2
(3)(-y-x)2
(4)(1-x)2
=16m2+8mn+n2
=a2-2ab+b2
=y2+2xy+x2
=1-2x+x2
练习.计算:(口答):
(5) (x+y)2
(6) (5a+b)2
(7)(3a-b)2
(8)(m-2n)2
=x2+2xy+y2
=25a2+10ab+b2
=9a2-6ab+b2
=m2-4mn+4n2
典例讲评
例1:运用完全平方公式计算:
(1)(4m+n)2
例2:运用完全平方公式计算:
(1)1022 (2)992
当堂训练
思考:(a+b)2与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
(a-b)2与a2-b2相等吗?为什么?
请尝试用多种方法求解上述例题。
当堂训练
拓展练习:
1. =_______;
2.若 是一个完全平方公式,
则 _______;
3.若 是一个完全平方公式,
则 _______;
1
4.请添加一项________,使得 是完全平方式.
知识点二:完全平方公式的常用变形
(1)a2+b2=(a+b)2-2ab=(a-b)2+2ab
完全平方公式的常见变形
一题多变:已知a-b=13,ab=-12,求下列各式的值:
知识点二:完全平方公式的常用变形
完全平方公式的常见变形
(2)(a+b)2+(a-b)2=2a2+2b2
知识点二:完全平方公式的常用变形
完全平方公式的常见变形
(3)(a+b)2-(a-b)2=4ab
(4)ab= [(a+b)2-(a2+b2)]=
知识点二:完全平方公式的常用变形
完全平方公式的常见变形
知识点二:完全平方公式的常用变形
(1)a2+b2=(a+b)2-2ab=(a-b)2+2ab
完全平方公式的常见变形
知识点三:添括号法则
我们学过去括号法则,即
口诀:去括号,看符号;
是“+”号,不变号;
是“-”号,全变号.
运用乘法公式计算,有时要在式子中添括号.把上面等式左右两边交换位置就得到:
a + b + c=a + (b+c)
a﹣b﹣c=a﹣(b+c)
a + (b+c)=a + b + c
a﹣(b+c)=a﹣b﹣c
知识点三:添括号法则
新知探究
填空:
(1)a+(b-c) = ;(2)a-(b-c)= ;
(3) a-(b+c)= ;(4)a-(-b-c)= .
根据上面四个等式填空:
(1)a+b-c=a+( ) (2) a-b+c=a-( )
(3)a-b-c=a-( ) (4) a+b+c=a-( )
观察这四个等式的左右两边,你发现了什么?
b-c
b-c
b+c
-b-c
a+b-c
a-b+c
a-b-c
a+b+c
新知归纳
知识点三:添括号法则
a + b – c = a + ( b – c)
a + b – c = a – ( – b +c )
符号均没有变化
符号均发生了变化
添上“+ ( )”, 括号里的各项都不变符号.
添上“– ( )”, 括号里的各项都改变符号.
口诀:
添括号,看符号;
添“+”号,不变号;
添“-”号,全变号.
新知归纳
知识点三:添括号法则
口诀:添括号,看符号;
添“+”号,不变号;
添“-”号,全变号.
添括号法则
添括号时,如果括号前面是“+”号,括到括号里的各项都不改变符号;
如果括号前面是“-”号,括到括号里的各项都要改变符号;
当堂训练
当堂训练
当堂训练
1.不改变代数式a2﹣(2a+b+c)的值,把它括号前面的符号变为相反的符号,应为( )
A.a2+(-2a+b+c) B.a2+(-2a-b-c)
C.a2+(-2a)+b+c D.a2-(-2a-b-c)
2.将多项式3x3-2x2+4x-5添括号后正确的是( )
A.3x3-(2x2+4x-5) B.(3x3+4x)-(2x2+5)
C.(3x3-5)+(﹣2x2-4x) D.2x2+(3x3+4x-5)
B
B
当堂检测
3.在下列各式的括号内填上适当的项.
(1)x3-3x2y+3xy2﹣y3=x3+( );
(2)2﹣x2+2xy﹣y2=2﹣( );
4.下列添括号错误的是( )
A.a2ーb2ーb+a=a2ーb2+(a-b)
B.(a+b+c)(aーbーc)=[a+(b+c)][a-(b+c)]
C.a﹣b+c﹣d=(a﹣d)+(c﹣b)
D.aーb=ー(b+a)
x2﹣2xy+y2
-3x2y+3xy2﹣y3
D
归纳总结
(1)在使用添括号法则时,要明确括到括号里的是哪些项,括号前面的符号是正号还是负号;
(2)添括号与去括号是互逆的,符号的变化是一致的,在运用添括号法则时,可与去括号法则相比较.注意不要只改变括号内部分项的符号;
(3)添括号比去括号容易出错,特别是当括号前添“﹣”号时,添括号后是否正确,可利用去括号法则检验.
null
典例讲评
null
当堂训练
利用乘法公式计算:
(1) (x+y+2)(x+y-2) ;(2) (a-b+c)(a+b-c).
null
当堂训练
达标检测
1.下列计算正确的是( )
A.(x+y)2=x2+y2 B.(x-y)2=x2-2xy-y2
C.(x+2y)(x-2y)=x2-2y2 D.(-x+y)2=x2-2xy+y2
2下列各式,计算结果是 m2n2 -m+1的是( )
A .(mn- )2 B. ( mn+1)2
C. ( mn-1)2 D. ( mn-1)2
3若(x-y)2=(x+y)2+( ),则括号中应填的是( )
A.-2xy B. 2xy C. -4xy D. 4xy
C
D
1
4
C
达标检测
4.将面积为a2的正方形边长均增加2,则正方形的面积增加了( )
A.4 B.2a+4 C.4a+4 D. 4a
5(易错题)计算:(3x-2y)2= ,
(-2t- )2= ,
C
9x2-12xy+4y2
达标检测
运用完全平方公式计算:
(1)1022 (2)992
解:(1) 1022 = (100+2)2= 1002+2×100×2+22
= 10000+400+4
= 10404
(2)992 = (100-1)2 =1002-2×100×1+12
= 10000-200+1
= 9801
达标检测
1.若(y+a)2=y2-6y+b,则a,b的值分别为( )
A.a=3,b=9 B.a= -3,b= -9
C.a=3,b= -9 D,a= -3,b=9
2.下列运算中,错误的有( )
①(2x+y)2=4x2+y2; ②(a-3b)2=a2-9b2 ;
③(-x-y)2=x2-2xy+y2; ④(x- )2=x2-x+
A.1个 B.2个 C.3个 D.4个
D
C
达标检测
3.( -3)2=16a2- + .
4.已知2x+y=1,则代数式(y+1)2-(y2-4x)的值为 .
5.如果y2-ky+9是完全平方式,则 k= .
6.利用完全平方公式计算:
(1)2012 (2)1992
3
4a
24ab
9b2
达标检测
2
null
达标检测
1.应用平方差公式计算(x+2y﹣1)(x﹣2y+1),则下列变形正确的是( )
A.[x﹣(2y+1)]2
B.[x+(2y+1)]2,
C.[x+(2y﹣1)][x﹣(2y﹣1)]
D.[(x﹣2y)+1][(x﹣2y)﹣1]
C
C
达标检测
2.下列式子中不能用乘法公式计算的是( )
A.(a+b﹣c)(a﹣b+c)
B.(a﹣b﹣c)2
C.(2a+b+2)(a﹣2b﹣2)
D.(2a+3b﹣1)(1﹣2a﹣3b).
C
null
达标检测
3.计算(a+1)2(a-1)2的结果是( )
A.a4-1 B.a4+1 C.a4+2a2+1 D.a4-2a2+1
4.利用乘法公式计算:
(1) (x+2y﹣3)(x﹣2y+3) ;(2) (a+b+c)2.
D
null
达标检测
5.利用乘法公式计算(变式练习):
(1) (3a+b﹣2)(3a﹣b+2) ;(2) (a+b﹣c)2;
(3) (2x+3y﹣1)(1+2x+3y)
