13.3 同位角、内错角、同旁内角 课件(67张PPT)
文档属性
| 名称 | 13.3 同位角、内错角、同旁内角 课件(67张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 317.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 00:00:00 | ||
图片预览










文档简介
(共67张PPT)
a
c
1
2
3
4
1、如图:直线a和直线c相交,得到几个小于
180度的角?
四个
2、这些角有哪些位置关系?
它们的大小有什么关系?
位置关系:对顶角和邻补角。
大小关系:对顶角相等,邻补角互补。
a
c
1
2
3
4
b
1
2
3
4
5
8
7
6
第一组
∠1,
∠2
∠3,
∠4
第二组:
∠5,∠6
∠7,∠8
?
被截直线
a
b
c
截线
1
2
3
4
5
8
7
6
这时我们把这种情形称为“直线c截直线a、b”或“直线a、b被直线c所截”。
直线c截直线a、b得到8个角
三线八角
∠1与∠5
∠2与∠6
∠3与∠7
∠4与∠8
8
b
a
l
1
2
3
4
5
6
7
1
5
下方)
(左边//
同一侧。
同一方
右边)
1:都在第三条直线L的
(上方/
2:都在直线a与直线b的
∠4与∠6
6
7
8
5
l
3
1
2
4
a
b
∠3与∠5
4
6
3
5
1:夹在直线a与直线b的内部。
内错角
2:在第三条直线L的两侧,位置交错。
∠4与∠5
∠3与∠6
4
5
3
6
1:都在第三条直线L的同旁
同旁内角
2:夹在两直线的内部
1
2
3
4
5
6
7
8
L
a
b
同位角
内错角
同旁内角
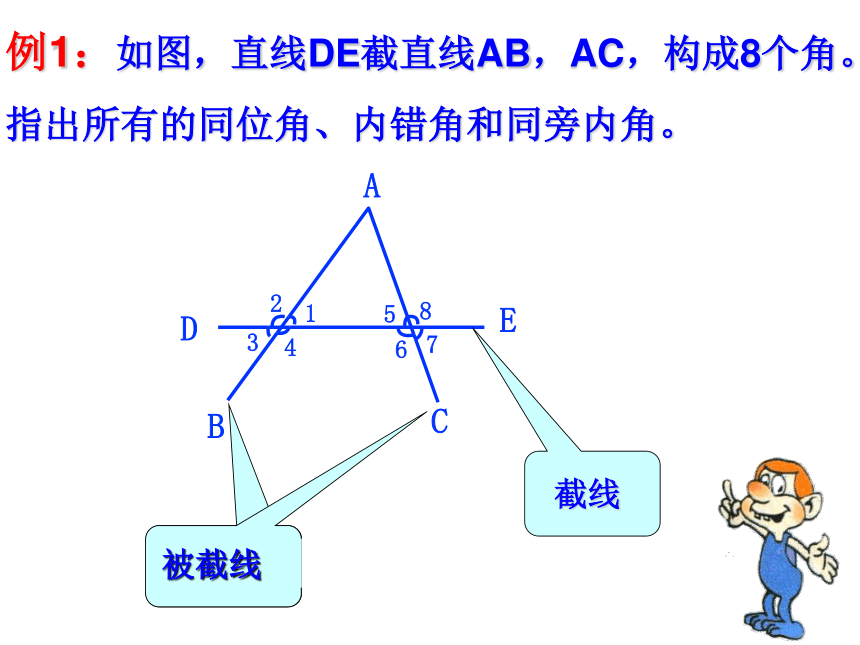
例1:如图,直线DE截直线AB,AC,构成8个角。指出所有的同位角、内错角和同旁内角。
截线
被截线
(1)如果把图看成是直线AB,EF被直线CD所截,那么∠1与∠2是一对什么角?
∠3与∠4呢?
∠
2与∠4呢?
(同位角)
(内错角)
(同旁内角)
练一练:
练一练:
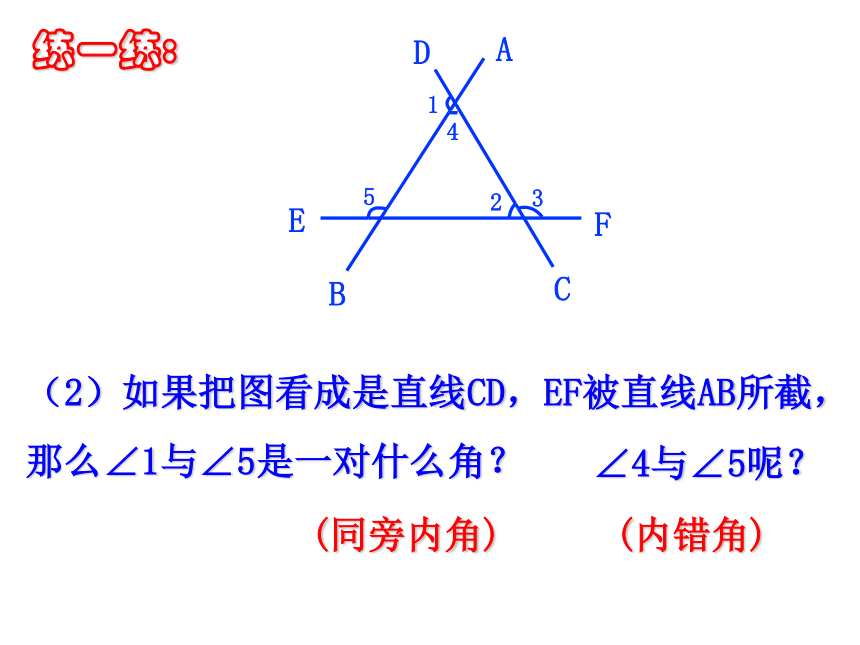
(2)如果把图看成是直线CD,EF被直线AB所截,那么∠1与∠5是一对什么角?
∠4与∠5呢?
(同旁内角)
(内错角)
练一练:
(3)哪两条直线被哪一条直线所截,∠2与∠5是同位角?
(直线AB和CD被直线EF所截)
1.同位角和同旁内角在位置上有什么
相同点和不同点?
2.内错角和同旁内角在位置上有什么相同点和不同点?
l
a
b
1
3
同位角
l
a
b
2
7
内错角
l
a
b
2
3
同旁内角
讨论:当两个角已经成为同位角,内错角或同旁内角时,一个角的两边与另一个角的两边有什么共同之处?
1
2
3
4
5
6
一个角的一条边与另一个角的一条边都在截线上。
同位角、内错角和同旁内角的结构特征:
下列图形中,∠1和∠2是否是同位
角?
判断:
1
2
1
2
1
1
2
1
2
2
注意:
同位角、内错角、同
旁内角存在的前提:三
线。
图形比较复杂时,应
当分解图形,一般留下
要用的“三线”。
(2)下面四个图形中,∠1和∠2是否是
内错角
选择:
1
2
2
1
1
2
1
2
(A)
(B)
(C)
(D)
课堂练习:
1、如图,(1)
和
是直线_____与直线____被直线______所截形成的__________。
(2)
和
是直线_____与直线____被直线______所截形成的_________。
4
3
2
1
A
B
C
D
内错角
BD
BC
AD
BD
CD
AB
内错角
1
4
1
4
1
4
2
3
2
3
2
3
1
4
A
B
C
D
2
3
A
B
D
C
(1)
(2)
2、图中,
与哪个角是内错角?
与哪个角是同旁内角?它们分别是有哪两条直线被哪一条直线截成的?
A
B
C
D
E
1
注意:
的同旁内角有三个。
D
A
E
B
C
1
D
A
E
B
C
1
D
A
E
B
C
1
A
B
C
1
A
B
C
1
A
B
C
1
1
B
C
A
1
B
C
A
1
B
C
A
图中∠B的同位角是
D
A
C
B
F
B
A
C
1
E
F
D
A
C
1
E
B
2
F
能力挑战:
1.
看图填空
(1)若ED,BF被AB所截,
则∠1与_____是同位角。
∠2
能力挑战:
看图填空
(2)若ED,BC被AF所截,
则∠3与_____是内错角。
∠4
能力挑战:
看图填空
(3)∠1与∠3是AB和AF被_____所截构成的_______角。
DE
内错
能力挑战:
看图填空
(4)∠2与∠4是_____和_____被
BC所截构成的______角。
AB
AF
同位
2.
如图,根据所标出的角填空:
1
2
3
4
5
6
∠1的同位角有
∠5的内错角有
∠2的同旁内角有
∠6是∠4的
角
∠3和∠6
∠3和∠6
∠3
同旁内角
练习
找出下列图中的同位角、内错角、同旁内角,并说明是由哪两条直线被哪条直线所截得到的?
E
A
D
B
C
5
3
4
1
2
(1)
D
A
C
E
B
2
1
4
3
(2)
找出下图中所有的
a
b
1
2
3
4
5
8
7
6
c
9
同位角
同位角:
∠1和∠5,∠4和∠8,
∠2和∠6,∠3和∠7
∠9和∠4,
∠9和∠5
找出下图中所有的
a
b
1
2
3
4
5
8
7
6
c
9
内错角
内错角
∠3和∠5,∠4和∠6
∠9和∠2
∠9和∠7
找出下图中所有的
a
b
1
2
3
4
5
8
7
6
c
9
同旁内角
同旁内角:
∠4和∠5,∠3和∠6
∠9和∠3
∠9和∠6
10
9
12
11
找出下图中所有的同位角、内错角、
同旁内角.
a
b
1
2
3
4
5
7
6
8
c
主要学习内容:
1、两条直线被第三条直线所截成的无公共
顶点的两个角的三种位置关系。
2、从图中出同位角、内错角、同旁内角。
小
结
截线
被截线
结构特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
A
B
C
E
D
1
2
4
3
2
1
3
4
A
B
C
D
A
B
C
E
F
1
2
3
4
判断图中∠1和∠2
、∠3和∠4各是哪两条直线被哪一条直线所截而成?它们各是什么角?
A
B
C
D
1
2
3
4
5
6
7
在∠1、∠2、∠3、∠4、∠5、∠6、∠7中,
(1)哪些是直线DC和AB被直线AC所截得的内错角?
(2)哪些是直线AD和BC被直线AC所截得的内错角?
(3)哪些是直线DC和AC被直线AD所截得的同位角?
(4)哪些是直线AC和AB被直线BC所截得的同旁内角?
2
5
1
4
1
7
3
4
名
称
内错角
同旁内角
同位角
位
置
特
征
交错、内部
在截线同旁、
内部
图
示
A
B
C
D
E
F
1
2
3
4
5
8
7
6
相同方位
每一对角的顶点不重合、有一边在同一条直线(截线)上,
例1:如图,直线DE、BC被直线AB所截。
∠1与∠2、∠1与∠3、∠1与∠4各
是什么角?
D
E
A
B
C
4
2
3
1
合作学习:
1.请找出图中所有的同位角、内错角和同旁内角。
练
习
1、找出下列各图中所有的同位角、
内错角、同旁内角。
c
a
b
1
2
3
4
5
6
7
8
a
b
c
1
2
3
4
练习:
下列图形中∠1与∠2是否是同位角?
若是,说明它们由哪两条直线被哪条
直线所截而成的,若不是说明理由。
a
b
c
1
2
a
b
c
1
2
练习
下列图形中∠1与∠2是否是内错角?若是,说明它们由哪两条直线被哪条直线所截而成的,若不是说明理由。
a
b
c
1
2
a
b
c
1
2
练习
下列图形中∠1与∠2是否是同旁内角?若是,说明它们由哪两条直线被哪条直线所截而成的,若不是说明理由。
a
b
c
1
2
a
b
c
1
2
例2:如图,直线DE交∠ABC的边BA于点F。如果内错角∠1与∠2相等,那么同位角∠1与∠4相等,同旁内角∠1与∠3互补。请说明理由。
例2:下列各角分别是由哪两条直线被哪一条
直线截成的?
a
b
c
1
2
∠1与∠2
是什么角?
a
b
c
2
3
∠2与∠3
是什么角?
a
b
c
4
5
∠4与∠5
是什么角?
总结:
同位角的基本图形:
内错角的基本图形:
同旁内角的基本图形:
小结:
三线八角中,有四对同位角,
两对内错角,两对
同旁内角。
要抓住八角的位置特征,分清
楚是哪两条直线被第三条直线所截
。
当图形复杂时,要学会画
分解图形。
a
c
b
1
2
3
4
5
8
7
6
例:如图,直线DE、BC被直线AB所截。
(1)∠1与∠2、∠1与∠3、∠1与∠4各是
什么角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?
1
4
2
3
A
B
C
D
E
证明:∵
∠1=∠4(已知)
又∵
∠2=∠4(对顶角相等)
∴
∠1=∠2(等量代换)
证明:∵∠2+∠3=180度(平角的定义)
又∵∠1=∠2(已证)
∴∠1+∠3=180度(等量代换)
∴∠1和∠3互补(补角的定义)
学过的角?
互为余角
互为补角
对顶角
两个角的和是90o
两个角的和是180o
如图,直线a,b相交形成四个角∠
1,∠
2,∠
3,∠
4
∠1与∠3
是对顶角
∠2与∠4是对顶角
余角
补角
对顶角
都是成对出现的
余角
补角
与位置无关
对顶角
与位置有关
1
2
3
4
a
b
思考:
一个平面内的两条直线有几种位置关系?
相交
平行
三条直线的位置关系,有下面四种情况:
一个交点
三个交点
两个交点
没有交点
“三线八角”
1)∠1与∠3在哪一条直线的同旁?
2)分别在哪两条直线的相同的一侧?
3)具有这样特点的角还有哪几对?
直线l.
直线a和b.
具有这样特点的角还有三对,∠2与∠4,∠5与∠7,∠6与∠8。
l
a
b
1
2
3
4
8
7
5
6
l
a
b
2
4
l
a
b
7
5
l
a
b
1
3
l
a
b
8
6
如∠1与∠3这样位置的一对角叫做同位角。同样的,∠2与∠4,∠5与∠7,∠6与∠8也是同位角。
1)∠2与∠7在哪一条直线的两旁?
2)在哪两条直线之间?
3)具有这样特点的角还有哪几对?
直线l.
直线a和b.
具有这样特点的角还有一对,∠3与∠6。
l
a
b
1
2
3
4
8
7
5
6
如∠2与∠7这样位置的一对角叫做内错角。同样的∠3与∠6也是内错角。
l
a
b
3
6
l
a
b
2
7
1)∠2与∠3在哪一条直线的同旁?
2)在哪两条直线之间?
3)具有这样特点的角还有哪几对?
直线l.
直线a和b.
具有这样特点的角还有一对,∠6与∠7。
l
a
b
1
2
3
4
8
7
5
6
小
结
1、这节课研究的是两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,即同位角、内错角、同旁内角。
2、同位角、内错角、同旁内角的特点:
与被截直线的关系
与截线的关系
同位角
内错角
同旁内角
被截直线的同一方向
被截直线之间
被截直线之间
截线的同旁
截线的两旁
截线的同旁
家庭作业:教材第68页2题;第71页9、10题。
例1
如图1-2,直线DE截AB,AC,构成8个角。指出所有的同位角、内错角和同旁内角。
1
2
3
4
5
6
7
8
A
B
C
D
E
例2
如图:直线DE交∠ABC的
边BA于点
F.
如果内错角∠1与∠2相等,那么同位角∠1与∠4相等,同旁内角∠1与∠3互补。请说明理由。
课内练习
A
B
C
D
E
F
1
2
3
4
5
1、(1)如果把图看成是直线AB,EF被直线CD所截,那么∠1与∠2是一对什么角 ∠3与∠4呢
∠2与∠4呢
(2)如果把图看成是直线CD,EF被直线AB所截,那么∠1与∠5是一对什么角
∠4与∠5呢
(3)哪两条直线被哪一条所截,∠2与∠5是同位角
1.同位角和同旁内角的相同点是,都在截线的一侧;不同点是,同位角在被截的两条直线的一侧,而同旁内角在被截的两条直线之间.
2.内错角和同旁内角的相同点是,都在被截的两条直线之间;不同点是,内错角在截线的两侧,而同旁内角在截线的一侧.
3.1)同位角,内错角和同旁内角都是不共顶点的角.2)它们有一个公共的边:截线.
1.看图填空:
1)直线a,b被直线c所截,所得的∠1与∠5是____
角,∠4与∠6是____
角,∠3与∠6是____
角。
2)直线c,d被直线a所截,同位角有____
对,它们是____
____
____
____
,
内错角有____
对,它们是____
____
,
同旁内角有____
对,它们是____
____
a
b
c
d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
同位
内错
同旁内
4
∠
1与∠9,
∠2
与∠10,
∠3与
∠11,
∠4与
∠12
2
2
∠
2与∠12,
∠3与
∠9
∠
2与∠9,
∠3与
∠12
a
b
c
d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.判断下列说法是否正确。
1)图中,∠6与∠12是同旁内角。
2)图中,∠13与∠14是邻补角。
3)图中,∠11与∠15是直线a,b被直线d所截得的同位角。
错.
对.
对.
3.写出图中的同位角,内错角和同旁内角。
B
C
A
E
1
2
3
4
5
分解出来的图形:
C
A
E
2
4
B
C
A
E
1
5
B
C
A
3
4
5
B
解:内错角:
∠
2与∠4;
同位角:
∠
1与∠5;
同旁内角:
∠
3与∠4,
∠3与∠5,∠4与
∠5.
B
C
A
E
1
2
3
说能出你这节课的收获和体验让大家与你分享吗?
解:
(1)中的∠1与∠2是同位角.
(2)中的∠3与∠4不是同位角.
4.如图,(1)中的∠1与∠2是同位角吗? (2)中的∠3与∠4呢?
(1)
1
2
(2)
3
4
例题:如图,直线DE与BC被直线AB所截。
(1)
与
、
与
、
与
各是什么角?
(2)如果
,那么
和
相等吗?
和
互补吗?为什么?
E
D
C
B
A
1
2
3
4
例2
如图
直线DE交∠ABC的边BC于点F。如果内错角∠1与∠2相等,那么同位角∠1与∠4相等,同旁内角∠1与∠3∠互补。请说明理由。
A
B
C
D
E
F
1
2
3
4
解:∵∠1=∠2
(已知)
∠2=∠4
(对顶角相等)
∴∠1=∠4
∵∠2+∠3=180°
(已知)
∴∠1+∠3=180°
例题:如图,直线DE与BC被直线AB所截。
(1)
与
、
与
、
与
各是什么角?
(2)如果
,那么
和
相等吗?
和
互补吗?为什么?
E
D
C
B
A
1
2
3
4
a
c
1
2
3
4
1、如图:直线a和直线c相交,得到几个小于
180度的角?
四个
2、这些角有哪些位置关系?
它们的大小有什么关系?
位置关系:对顶角和邻补角。
大小关系:对顶角相等,邻补角互补。
a
c
1
2
3
4
b
1
2
3
4
5
8
7
6
第一组
∠1,
∠2
∠3,
∠4
第二组:
∠5,∠6
∠7,∠8
?
被截直线
a
b
c
截线
1
2
3
4
5
8
7
6
这时我们把这种情形称为“直线c截直线a、b”或“直线a、b被直线c所截”。
直线c截直线a、b得到8个角
三线八角
∠1与∠5
∠2与∠6
∠3与∠7
∠4与∠8
8
b
a
l
1
2
3
4
5
6
7
1
5
下方)
(左边//
同一侧。
同一方
右边)
1:都在第三条直线L的
(上方/
2:都在直线a与直线b的
∠4与∠6
6
7
8
5
l
3
1
2
4
a
b
∠3与∠5
4
6
3
5
1:夹在直线a与直线b的内部。
内错角
2:在第三条直线L的两侧,位置交错。
∠4与∠5
∠3与∠6
4
5
3
6
1:都在第三条直线L的同旁
同旁内角
2:夹在两直线的内部
1
2
3
4
5
6
7
8
L
a
b
同位角
内错角
同旁内角
例1:如图,直线DE截直线AB,AC,构成8个角。指出所有的同位角、内错角和同旁内角。
截线
被截线
(1)如果把图看成是直线AB,EF被直线CD所截,那么∠1与∠2是一对什么角?
∠3与∠4呢?
∠
2与∠4呢?
(同位角)
(内错角)
(同旁内角)
练一练:
练一练:
(2)如果把图看成是直线CD,EF被直线AB所截,那么∠1与∠5是一对什么角?
∠4与∠5呢?
(同旁内角)
(内错角)
练一练:
(3)哪两条直线被哪一条直线所截,∠2与∠5是同位角?
(直线AB和CD被直线EF所截)
1.同位角和同旁内角在位置上有什么
相同点和不同点?
2.内错角和同旁内角在位置上有什么相同点和不同点?
l
a
b
1
3
同位角
l
a
b
2
7
内错角
l
a
b
2
3
同旁内角
讨论:当两个角已经成为同位角,内错角或同旁内角时,一个角的两边与另一个角的两边有什么共同之处?
1
2
3
4
5
6
一个角的一条边与另一个角的一条边都在截线上。
同位角、内错角和同旁内角的结构特征:
下列图形中,∠1和∠2是否是同位
角?
判断:
1
2
1
2
1
1
2
1
2
2
注意:
同位角、内错角、同
旁内角存在的前提:三
线。
图形比较复杂时,应
当分解图形,一般留下
要用的“三线”。
(2)下面四个图形中,∠1和∠2是否是
内错角
选择:
1
2
2
1
1
2
1
2
(A)
(B)
(C)
(D)
课堂练习:
1、如图,(1)
和
是直线_____与直线____被直线______所截形成的__________。
(2)
和
是直线_____与直线____被直线______所截形成的_________。
4
3
2
1
A
B
C
D
内错角
BD
BC
AD
BD
CD
AB
内错角
1
4
1
4
1
4
2
3
2
3
2
3
1
4
A
B
C
D
2
3
A
B
D
C
(1)
(2)
2、图中,
与哪个角是内错角?
与哪个角是同旁内角?它们分别是有哪两条直线被哪一条直线截成的?
A
B
C
D
E
1
注意:
的同旁内角有三个。
D
A
E
B
C
1
D
A
E
B
C
1
D
A
E
B
C
1
A
B
C
1
A
B
C
1
A
B
C
1
1
B
C
A
1
B
C
A
1
B
C
A
图中∠B的同位角是
D
A
C
B
F
B
A
C
1
E
F
D
A
C
1
E
B
2
F
能力挑战:
1.
看图填空
(1)若ED,BF被AB所截,
则∠1与_____是同位角。
∠2
能力挑战:
看图填空
(2)若ED,BC被AF所截,
则∠3与_____是内错角。
∠4
能力挑战:
看图填空
(3)∠1与∠3是AB和AF被_____所截构成的_______角。
DE
内错
能力挑战:
看图填空
(4)∠2与∠4是_____和_____被
BC所截构成的______角。
AB
AF
同位
2.
如图,根据所标出的角填空:
1
2
3
4
5
6
∠1的同位角有
∠5的内错角有
∠2的同旁内角有
∠6是∠4的
角
∠3和∠6
∠3和∠6
∠3
同旁内角
练习
找出下列图中的同位角、内错角、同旁内角,并说明是由哪两条直线被哪条直线所截得到的?
E
A
D
B
C
5
3
4
1
2
(1)
D
A
C
E
B
2
1
4
3
(2)
找出下图中所有的
a
b
1
2
3
4
5
8
7
6
c
9
同位角
同位角:
∠1和∠5,∠4和∠8,
∠2和∠6,∠3和∠7
∠9和∠4,
∠9和∠5
找出下图中所有的
a
b
1
2
3
4
5
8
7
6
c
9
内错角
内错角
∠3和∠5,∠4和∠6
∠9和∠2
∠9和∠7
找出下图中所有的
a
b
1
2
3
4
5
8
7
6
c
9
同旁内角
同旁内角:
∠4和∠5,∠3和∠6
∠9和∠3
∠9和∠6
10
9
12
11
找出下图中所有的同位角、内错角、
同旁内角.
a
b
1
2
3
4
5
7
6
8
c
主要学习内容:
1、两条直线被第三条直线所截成的无公共
顶点的两个角的三种位置关系。
2、从图中出同位角、内错角、同旁内角。
小
结
截线
被截线
结构特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
A
B
C
E
D
1
2
4
3
2
1
3
4
A
B
C
D
A
B
C
E
F
1
2
3
4
判断图中∠1和∠2
、∠3和∠4各是哪两条直线被哪一条直线所截而成?它们各是什么角?
A
B
C
D
1
2
3
4
5
6
7
在∠1、∠2、∠3、∠4、∠5、∠6、∠7中,
(1)哪些是直线DC和AB被直线AC所截得的内错角?
(2)哪些是直线AD和BC被直线AC所截得的内错角?
(3)哪些是直线DC和AC被直线AD所截得的同位角?
(4)哪些是直线AC和AB被直线BC所截得的同旁内角?
2
5
1
4
1
7
3
4
名
称
内错角
同旁内角
同位角
位
置
特
征
交错、内部
在截线同旁、
内部
图
示
A
B
C
D
E
F
1
2
3
4
5
8
7
6
相同方位
每一对角的顶点不重合、有一边在同一条直线(截线)上,
例1:如图,直线DE、BC被直线AB所截。
∠1与∠2、∠1与∠3、∠1与∠4各
是什么角?
D
E
A
B
C
4
2
3
1
合作学习:
1.请找出图中所有的同位角、内错角和同旁内角。
练
习
1、找出下列各图中所有的同位角、
内错角、同旁内角。
c
a
b
1
2
3
4
5
6
7
8
a
b
c
1
2
3
4
练习:
下列图形中∠1与∠2是否是同位角?
若是,说明它们由哪两条直线被哪条
直线所截而成的,若不是说明理由。
a
b
c
1
2
a
b
c
1
2
练习
下列图形中∠1与∠2是否是内错角?若是,说明它们由哪两条直线被哪条直线所截而成的,若不是说明理由。
a
b
c
1
2
a
b
c
1
2
练习
下列图形中∠1与∠2是否是同旁内角?若是,说明它们由哪两条直线被哪条直线所截而成的,若不是说明理由。
a
b
c
1
2
a
b
c
1
2
例2:如图,直线DE交∠ABC的边BA于点F。如果内错角∠1与∠2相等,那么同位角∠1与∠4相等,同旁内角∠1与∠3互补。请说明理由。
例2:下列各角分别是由哪两条直线被哪一条
直线截成的?
a
b
c
1
2
∠1与∠2
是什么角?
a
b
c
2
3
∠2与∠3
是什么角?
a
b
c
4
5
∠4与∠5
是什么角?
总结:
同位角的基本图形:
内错角的基本图形:
同旁内角的基本图形:
小结:
三线八角中,有四对同位角,
两对内错角,两对
同旁内角。
要抓住八角的位置特征,分清
楚是哪两条直线被第三条直线所截
。
当图形复杂时,要学会画
分解图形。
a
c
b
1
2
3
4
5
8
7
6
例:如图,直线DE、BC被直线AB所截。
(1)∠1与∠2、∠1与∠3、∠1与∠4各是
什么角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?
1
4
2
3
A
B
C
D
E
证明:∵
∠1=∠4(已知)
又∵
∠2=∠4(对顶角相等)
∴
∠1=∠2(等量代换)
证明:∵∠2+∠3=180度(平角的定义)
又∵∠1=∠2(已证)
∴∠1+∠3=180度(等量代换)
∴∠1和∠3互补(补角的定义)
学过的角?
互为余角
互为补角
对顶角
两个角的和是90o
两个角的和是180o
如图,直线a,b相交形成四个角∠
1,∠
2,∠
3,∠
4
∠1与∠3
是对顶角
∠2与∠4是对顶角
余角
补角
对顶角
都是成对出现的
余角
补角
与位置无关
对顶角
与位置有关
1
2
3
4
a
b
思考:
一个平面内的两条直线有几种位置关系?
相交
平行
三条直线的位置关系,有下面四种情况:
一个交点
三个交点
两个交点
没有交点
“三线八角”
1)∠1与∠3在哪一条直线的同旁?
2)分别在哪两条直线的相同的一侧?
3)具有这样特点的角还有哪几对?
直线l.
直线a和b.
具有这样特点的角还有三对,∠2与∠4,∠5与∠7,∠6与∠8。
l
a
b
1
2
3
4
8
7
5
6
l
a
b
2
4
l
a
b
7
5
l
a
b
1
3
l
a
b
8
6
如∠1与∠3这样位置的一对角叫做同位角。同样的,∠2与∠4,∠5与∠7,∠6与∠8也是同位角。
1)∠2与∠7在哪一条直线的两旁?
2)在哪两条直线之间?
3)具有这样特点的角还有哪几对?
直线l.
直线a和b.
具有这样特点的角还有一对,∠3与∠6。
l
a
b
1
2
3
4
8
7
5
6
如∠2与∠7这样位置的一对角叫做内错角。同样的∠3与∠6也是内错角。
l
a
b
3
6
l
a
b
2
7
1)∠2与∠3在哪一条直线的同旁?
2)在哪两条直线之间?
3)具有这样特点的角还有哪几对?
直线l.
直线a和b.
具有这样特点的角还有一对,∠6与∠7。
l
a
b
1
2
3
4
8
7
5
6
小
结
1、这节课研究的是两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,即同位角、内错角、同旁内角。
2、同位角、内错角、同旁内角的特点:
与被截直线的关系
与截线的关系
同位角
内错角
同旁内角
被截直线的同一方向
被截直线之间
被截直线之间
截线的同旁
截线的两旁
截线的同旁
家庭作业:教材第68页2题;第71页9、10题。
例1
如图1-2,直线DE截AB,AC,构成8个角。指出所有的同位角、内错角和同旁内角。
1
2
3
4
5
6
7
8
A
B
C
D
E
例2
如图:直线DE交∠ABC的
边BA于点
F.
如果内错角∠1与∠2相等,那么同位角∠1与∠4相等,同旁内角∠1与∠3互补。请说明理由。
课内练习
A
B
C
D
E
F
1
2
3
4
5
1、(1)如果把图看成是直线AB,EF被直线CD所截,那么∠1与∠2是一对什么角 ∠3与∠4呢
∠2与∠4呢
(2)如果把图看成是直线CD,EF被直线AB所截,那么∠1与∠5是一对什么角
∠4与∠5呢
(3)哪两条直线被哪一条所截,∠2与∠5是同位角
1.同位角和同旁内角的相同点是,都在截线的一侧;不同点是,同位角在被截的两条直线的一侧,而同旁内角在被截的两条直线之间.
2.内错角和同旁内角的相同点是,都在被截的两条直线之间;不同点是,内错角在截线的两侧,而同旁内角在截线的一侧.
3.1)同位角,内错角和同旁内角都是不共顶点的角.2)它们有一个公共的边:截线.
1.看图填空:
1)直线a,b被直线c所截,所得的∠1与∠5是____
角,∠4与∠6是____
角,∠3与∠6是____
角。
2)直线c,d被直线a所截,同位角有____
对,它们是____
____
____
____
,
内错角有____
对,它们是____
____
,
同旁内角有____
对,它们是____
____
a
b
c
d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
同位
内错
同旁内
4
∠
1与∠9,
∠2
与∠10,
∠3与
∠11,
∠4与
∠12
2
2
∠
2与∠12,
∠3与
∠9
∠
2与∠9,
∠3与
∠12
a
b
c
d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.判断下列说法是否正确。
1)图中,∠6与∠12是同旁内角。
2)图中,∠13与∠14是邻补角。
3)图中,∠11与∠15是直线a,b被直线d所截得的同位角。
错.
对.
对.
3.写出图中的同位角,内错角和同旁内角。
B
C
A
E
1
2
3
4
5
分解出来的图形:
C
A
E
2
4
B
C
A
E
1
5
B
C
A
3
4
5
B
解:内错角:
∠
2与∠4;
同位角:
∠
1与∠5;
同旁内角:
∠
3与∠4,
∠3与∠5,∠4与
∠5.
B
C
A
E
1
2
3
说能出你这节课的收获和体验让大家与你分享吗?
解:
(1)中的∠1与∠2是同位角.
(2)中的∠3与∠4不是同位角.
4.如图,(1)中的∠1与∠2是同位角吗? (2)中的∠3与∠4呢?
(1)
1
2
(2)
3
4
例题:如图,直线DE与BC被直线AB所截。
(1)
与
、
与
、
与
各是什么角?
(2)如果
,那么
和
相等吗?
和
互补吗?为什么?
E
D
C
B
A
1
2
3
4
例2
如图
直线DE交∠ABC的边BC于点F。如果内错角∠1与∠2相等,那么同位角∠1与∠4相等,同旁内角∠1与∠3∠互补。请说明理由。
A
B
C
D
E
F
1
2
3
4
解:∵∠1=∠2
(已知)
∠2=∠4
(对顶角相等)
∴∠1=∠4
∵∠2+∠3=180°
(已知)
∴∠1+∠3=180°
例题:如图,直线DE与BC被直线AB所截。
(1)
与
、
与
、
与
各是什么角?
(2)如果
,那么
和
相等吗?
和
互补吗?为什么?
E
D
C
B
A
1
2
3
4
