13.3 同位角、内错角、同旁内角 课件(17张)
文档属性
| 名称 | 13.3 同位角、内错角、同旁内角 课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 92.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
13.3
同位角、内错角、同旁内角
问题1
如图,两条直线
a
、l
相交于点P,会构成几个角,这些角有什么样的位置和数量关系?
(1)位置关系
a
l
P
1
3
2
4
对顶角(2对):
∠1与∠3
∠2与∠4
邻补角(4对):
∠1与∠2
∠1与∠4
∠3与∠2
∠3与∠4
(2)数量关系
有一个公共顶点.
创设问题情境
对顶角相等、邻补角互补
问题2
若两条直线被第三条直线所截,那么交点最少有几个?最多有几个?先作图,再根据图形回答问题
(1)
(2)
(3)
a
l
P
1
3
2
4
b
Q
如图,在同一平面内,直线l与直线
a、b分别相交
于点P、Q,这样的情形可以说成
:
直线a、b被直线l所截
直线l叫做:
截线
图中有几条直线?构成了几个角?
“三线八角”图
5
6
7
8
角的名称
基本图形
角的特征
共有几对
位置特征
共同特征
在被截二直线a、b
在截线l
同位角
内错角
同旁内角
a
l
P
1
3
2
4
b
Q
5
6
7
8
观察
归纳
同位角:
∠1与∠5
∠2与∠6
∠4与∠8
∠3与∠7
内错角:
∠2与∠8
∠3与∠5
同旁内角:
∠2与∠5
∠3与∠8
b
l
a
8
7
6
5
4
3
2
1
例题1:指出图中的同位角、内错角、同旁内角.并说明它们是哪两条直线被哪一条直线所截得到的.
同位角:
∠1与∠3
∠2与∠4
∠5与∠7
∠6与∠8
内错角:
∠2与∠7
∠3与∠6
同旁内角:
∠2与∠3
∠6与∠7
直线a、b被直线l所截
新知应用
m
q
n
2
3
6
7
1
4
5
8
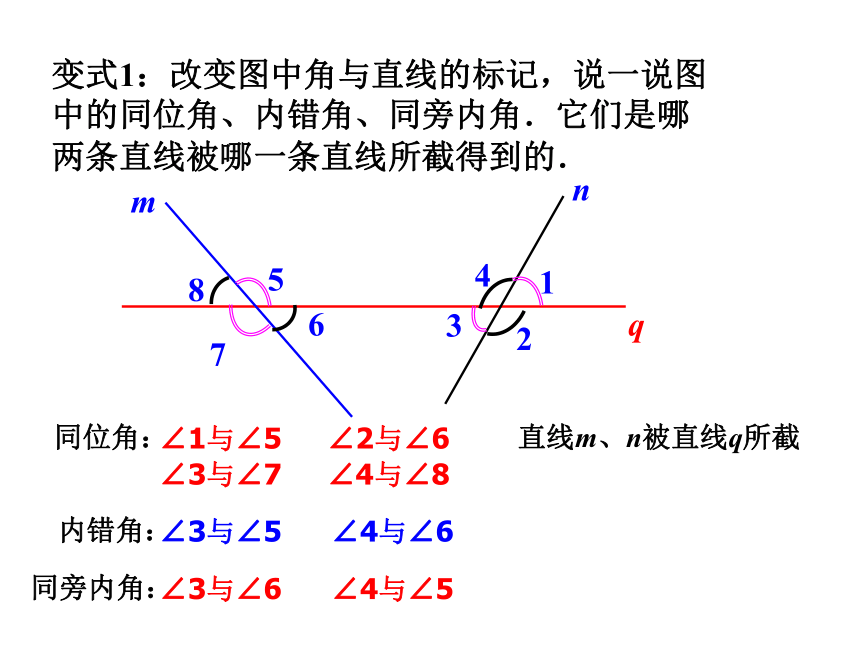
变式1:改变图中角与直线的标记,说一说图中的同位角、内错角、同旁内角.它们是哪两条直线被哪一条直线所截得到的.
同位角:
∠1与∠5
∠2与∠6
∠3与∠7
∠4与∠8
内错角:
∠3与∠5
∠4与∠6
同旁内角:
∠3与∠6
∠4与∠5
直线m、n被直线q所截
b
l
a
8
7
6
5
4
3
2
1
变式2:延伸被截直线a、b,得到下图.
在直线b、
l被直线a所截得的角中,找出同位角、内错角、同旁内角.
9
11
12
10
同位角:
∠3与∠10
∠4与∠11
∠7与∠9
∠8与∠12
内错角:
∠7与∠11
∠8与∠10
同旁内角:
∠7与∠10
∠8与∠11
b
l
a
8
7
6
5
4
3
2
1
变式2:
∠6与∠9是哪两条直线被哪一条直线所截得的内错角?
9
11
12
10
是直线a、
l被直线b所截得的
同位角、内错角、同旁内角的
识别关键
:
找到截线
(每对角各有一条边在截线上.)
b
l
a
8
7
6
5
4
3
2
1
变式3
直线a、b,交于点D,得到下图.
D
与∠D是同位角的是(
);
∠2
∠3
与∠D是内错角的是(
);
∠5
∠8
与∠D是同旁内角的是(
);
∠6
∠7
每对角各有一条边在截线上.
b
l
a
8
7
6
5
4
3
2
1
9
11
12
10
如何从比较复杂的图形中,正确找出同位角、内错角、
同旁内角呢?
一看角的顶点
(每对角的顶点不重合)
二看角的边
(每对角各有一条边在截线上)
三看角的方位
(在截线的同旁或两旁,
在两条被截直线的同侧或之间)
关键:
确定截线、找到特征图形
小结
A
B
C
D
1
2
3
4
5
6
7
变式4
下图中的内错角有几对?
以AB为截线的同旁内角有那几对?
自主小结
两条直线被第三条直线所截,得到
:
在每对角中:
三类角的识别
:
同位角、内错角、同旁内角.
角的顶点不重合;
一看角的顶点;二看角的边;三看角的方位.
最关键:截线的确定
各有一条边在截线上.
同位角的基本图形:
F型
内错角的基本图形:
Z型
同旁内角的基本图形:
C型
b
l
a
3
2
1
如图,
∠1和∠2是同位角吗
∠1和∠3呢
练习
c
∠1和∠2
同位角
∠1和∠3
同位角
不是
是
D
A
3
2
1
判断题:如图
练习
E
B
C
4
5
(1)∠D与∠5是同位角(
);
∠D与∠ACE是同位角(
).
(2)∠1与∠5是内错角(
);
∠2与∠4是内错角(
).
(3)∠B与∠D是同旁内角(
);
∠2与∠3是同旁内角(
).
√
×
√
√
×
√
练习
指出下图中的同位角,并说明每对同位角
是哪两条直线被哪一条直线所截得到的?
同位角:
直线DE、AB被直线AC所截
∠1与∠B
直线DE、BC被直线AB所截
∠2与∠C
直线DE、BC被直线AC所截
∠3与∠A
直线DE、AC被直线AB所截
∠4与∠A
还有吗?
不重复、不遗漏:
所有顶点的角都要考虑.
拓展
如图,图中有几对同旁内角?
∠
DAC
与∠
C
∠
EAB
与∠
B
∠
B
与∠
C
∠
BAC
与∠
C
∠
BAC
与∠
B
要有序
先简单,再到复合角
A
B
C
用三个大写字母表示
13.3
同位角、内错角、同旁内角
问题1
如图,两条直线
a
、l
相交于点P,会构成几个角,这些角有什么样的位置和数量关系?
(1)位置关系
a
l
P
1
3
2
4
对顶角(2对):
∠1与∠3
∠2与∠4
邻补角(4对):
∠1与∠2
∠1与∠4
∠3与∠2
∠3与∠4
(2)数量关系
有一个公共顶点.
创设问题情境
对顶角相等、邻补角互补
问题2
若两条直线被第三条直线所截,那么交点最少有几个?最多有几个?先作图,再根据图形回答问题
(1)
(2)
(3)
a
l
P
1
3
2
4
b
Q
如图,在同一平面内,直线l与直线
a、b分别相交
于点P、Q,这样的情形可以说成
:
直线a、b被直线l所截
直线l叫做:
截线
图中有几条直线?构成了几个角?
“三线八角”图
5
6
7
8
角的名称
基本图形
角的特征
共有几对
位置特征
共同特征
在被截二直线a、b
在截线l
同位角
内错角
同旁内角
a
l
P
1
3
2
4
b
Q
5
6
7
8
观察
归纳
同位角:
∠1与∠5
∠2与∠6
∠4与∠8
∠3与∠7
内错角:
∠2与∠8
∠3与∠5
同旁内角:
∠2与∠5
∠3与∠8
b
l
a
8
7
6
5
4
3
2
1
例题1:指出图中的同位角、内错角、同旁内角.并说明它们是哪两条直线被哪一条直线所截得到的.
同位角:
∠1与∠3
∠2与∠4
∠5与∠7
∠6与∠8
内错角:
∠2与∠7
∠3与∠6
同旁内角:
∠2与∠3
∠6与∠7
直线a、b被直线l所截
新知应用
m
q
n
2
3
6
7
1
4
5
8
变式1:改变图中角与直线的标记,说一说图中的同位角、内错角、同旁内角.它们是哪两条直线被哪一条直线所截得到的.
同位角:
∠1与∠5
∠2与∠6
∠3与∠7
∠4与∠8
内错角:
∠3与∠5
∠4与∠6
同旁内角:
∠3与∠6
∠4与∠5
直线m、n被直线q所截
b
l
a
8
7
6
5
4
3
2
1
变式2:延伸被截直线a、b,得到下图.
在直线b、
l被直线a所截得的角中,找出同位角、内错角、同旁内角.
9
11
12
10
同位角:
∠3与∠10
∠4与∠11
∠7与∠9
∠8与∠12
内错角:
∠7与∠11
∠8与∠10
同旁内角:
∠7与∠10
∠8与∠11
b
l
a
8
7
6
5
4
3
2
1
变式2:
∠6与∠9是哪两条直线被哪一条直线所截得的内错角?
9
11
12
10
是直线a、
l被直线b所截得的
同位角、内错角、同旁内角的
识别关键
:
找到截线
(每对角各有一条边在截线上.)
b
l
a
8
7
6
5
4
3
2
1
变式3
直线a、b,交于点D,得到下图.
D
与∠D是同位角的是(
);
∠2
∠3
与∠D是内错角的是(
);
∠5
∠8
与∠D是同旁内角的是(
);
∠6
∠7
每对角各有一条边在截线上.
b
l
a
8
7
6
5
4
3
2
1
9
11
12
10
如何从比较复杂的图形中,正确找出同位角、内错角、
同旁内角呢?
一看角的顶点
(每对角的顶点不重合)
二看角的边
(每对角各有一条边在截线上)
三看角的方位
(在截线的同旁或两旁,
在两条被截直线的同侧或之间)
关键:
确定截线、找到特征图形
小结
A
B
C
D
1
2
3
4
5
6
7
变式4
下图中的内错角有几对?
以AB为截线的同旁内角有那几对?
自主小结
两条直线被第三条直线所截,得到
:
在每对角中:
三类角的识别
:
同位角、内错角、同旁内角.
角的顶点不重合;
一看角的顶点;二看角的边;三看角的方位.
最关键:截线的确定
各有一条边在截线上.
同位角的基本图形:
F型
内错角的基本图形:
Z型
同旁内角的基本图形:
C型
b
l
a
3
2
1
如图,
∠1和∠2是同位角吗
∠1和∠3呢
练习
c
∠1和∠2
同位角
∠1和∠3
同位角
不是
是
D
A
3
2
1
判断题:如图
练习
E
B
C
4
5
(1)∠D与∠5是同位角(
);
∠D与∠ACE是同位角(
).
(2)∠1与∠5是内错角(
);
∠2与∠4是内错角(
).
(3)∠B与∠D是同旁内角(
);
∠2与∠3是同旁内角(
).
√
×
√
√
×
√
练习
指出下图中的同位角,并说明每对同位角
是哪两条直线被哪一条直线所截得到的?
同位角:
直线DE、AB被直线AC所截
∠1与∠B
直线DE、BC被直线AB所截
∠2与∠C
直线DE、BC被直线AC所截
∠3与∠A
直线DE、AC被直线AB所截
∠4与∠A
还有吗?
不重复、不遗漏:
所有顶点的角都要考虑.
拓展
如图,图中有几对同旁内角?
∠
DAC
与∠
C
∠
EAB
与∠
B
∠
B
与∠
C
∠
BAC
与∠
C
∠
BAC
与∠
B
要有序
先简单,再到复合角
A
B
C
用三个大写字母表示
