13.3 同位角、内错角、同旁内角 课件(17张PPT)
文档属性
| 名称 | 13.3 同位角、内错角、同旁内角 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 135.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
直线a和直线b相交于点o,得到几个小于180度的角?
a
这些角有哪些位置关系和数量关系?
1
2
3
4
四个
两种位置关系:
互为对顶角和互为邻补角.
对顶角相等,邻补角互补.
b
o
被截直线
a
b
c
截线
1
2
3
4
5
8
7
6
这时我们把这种情形称为“直线a、b被直线c所截”.
直线c截直线a、b得到几个角?
8个
两个角都在截线的(
)侧,又分别处在被截直线(
)侧.
∠1在截线c的(
)侧,在直线a的(
)方.
a
b
c
1
2
3
4
5
8
7
6
同位角
右
上
∠5在截线c的(
)侧,在直线b的(
)方.
右
上
图中共有(
)对同位角,它们是
∠1和∠5
,∠4和∠8,
∠2和∠6
,∠3和∠7
.
4
同
同
两个角都在截线的(
)侧,又在被截直线(
)侧.
a
b
c
1
2
3
4
5
8
7
6
图中共有(
)对
内错角,它们是:
∠3和∠5
,∠4
和∠6
2
∠3在截线c的(
)侧,在直线a、b的(
)侧.
左
内
∠5在截线c的(
)侧,在直线a、b的(
)侧.
右
内
两
内
内错角
∠6在截线c的(
)侧,在直线a、b的(
)侧.
两个角都在截线的(
)侧,又在被截直线(
)侧.
图中共有(
)对
同旁内角,它们是:
∠3和∠6
,∠4
和∠5
2
∠3在截线c的(
)侧,在直线a、b的(
)侧.
左
内
左
内
同
内
同旁内角
a
b
c
1
2
3
4
5
8
7
6
同位角
内错角
同旁内角
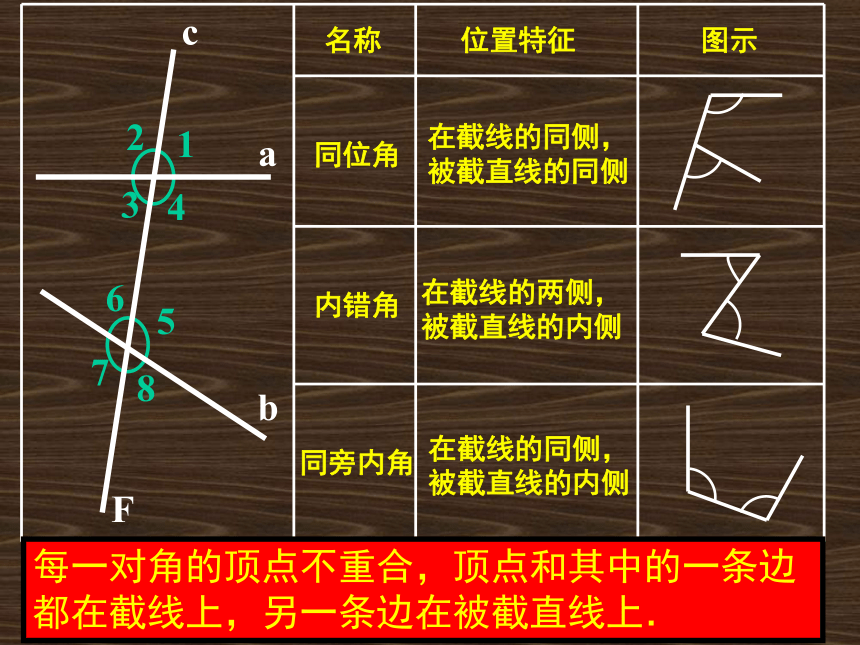
名称
内错角
同旁内角
同位角
位置特征
在截线的两侧,
被截直线的内侧
在截线的同侧,
被截直线的内侧
图示
a
b
c
F
1
2
3
4
5
8
7
6
在截线的同侧,
被截直线的同侧
每一对角的顶点不重合,顶点和其中的一条边
都在截线上,另一条边在被截直线上.
a
b
1
2
3
4
5
8
7
6
c
同位角:
∠1和∠5
∠4和∠8
∠2和∠6
∠3和∠7
∠9和∠4
找出下图中所有的同位角:
9
∠9和∠5
a
b
1
2
3
4
5
8
7
6
c
9
内错角:
∠3和∠5
∠4和∠6
∠9和∠2
找出下图中所有的内错角:
∠9和∠7
a
b
1
2
3
4
5
8
7
6
c
9
同旁内角:
∠3和∠6
∠4和∠5
∠9和∠3
找出下图中所有的同旁内角:
∠9和∠6
10
9
12
11
a
b
1
2
3
4
5
7
6
8
找出下图中所有的同位角、内错角
同旁内角:
2
判断:下列图形中,∠1和∠2是否是同位角?
1
2
1
2
1
1
2
1
2
注意:
同位角、内错角、同
旁内角存在的前提:三
线.
图形比较复杂时,应
当分解图形,一般留下
要用的“三线”.
×
√
√
√
√
选择:下面四个图形中,∠1和∠2不是内错
角的是(
)
1
2
2
1
1
2
1
2
(A)
(B)
(C)
(D)
A
A
B
C
D
1
2
3
4
5
6
7
在∠1、∠2、∠3、∠4、∠5、∠6、∠7中,
(1)哪些是直线DC和AB被直线AC所截得的内错角?
(2)哪些是直线AD和BC被直线AC所截得的内错角?
(3)哪些是直线DC和AC被直线AD所截得的同位角?
(4)哪些是直线AC和AB被直线BC所截得的同旁内角?
A
B
C
E
D
1
2
4
3
2
1
3
4
A
B
C
D
A
B
C
E
F
1
2
3
4
判断:图中∠1和∠2
、∠3和∠4各是哪两条直线被哪一条直线所截而成?它们各是什么角?
证明:
∵∠1=∠4(已知)
∠4+∠3=180度(邻补角的意义)
∴∠1+∠3=180度(等量代换)
∴∠1和∠3互补(互补的意义)
例:如图,直线DE、BC被直线AB所截.
(1)∠1与∠2、∠1与∠3、∠1与∠4各是
什么角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?
1
4
2
3
A
B
C
D
E
证明:
∵
∠1=∠4(已知)
∠2=∠4(对顶角相等)
∴
∠1=∠2(等量代换)
小结:
1、三线八角中,有四对同位角,两对内错角,
两对同旁内角.
2、要抓住八角的位置特征,分清楚是哪两条
直线被第三条直线所截
.
3、当图形复杂时,要学会画分解图形.
直线a和直线b相交于点o,得到几个小于180度的角?
a
这些角有哪些位置关系和数量关系?
1
2
3
4
四个
两种位置关系:
互为对顶角和互为邻补角.
对顶角相等,邻补角互补.
b
o
被截直线
a
b
c
截线
1
2
3
4
5
8
7
6
这时我们把这种情形称为“直线a、b被直线c所截”.
直线c截直线a、b得到几个角?
8个
两个角都在截线的(
)侧,又分别处在被截直线(
)侧.
∠1在截线c的(
)侧,在直线a的(
)方.
a
b
c
1
2
3
4
5
8
7
6
同位角
右
上
∠5在截线c的(
)侧,在直线b的(
)方.
右
上
图中共有(
)对同位角,它们是
∠1和∠5
,∠4和∠8,
∠2和∠6
,∠3和∠7
.
4
同
同
两个角都在截线的(
)侧,又在被截直线(
)侧.
a
b
c
1
2
3
4
5
8
7
6
图中共有(
)对
内错角,它们是:
∠3和∠5
,∠4
和∠6
2
∠3在截线c的(
)侧,在直线a、b的(
)侧.
左
内
∠5在截线c的(
)侧,在直线a、b的(
)侧.
右
内
两
内
内错角
∠6在截线c的(
)侧,在直线a、b的(
)侧.
两个角都在截线的(
)侧,又在被截直线(
)侧.
图中共有(
)对
同旁内角,它们是:
∠3和∠6
,∠4
和∠5
2
∠3在截线c的(
)侧,在直线a、b的(
)侧.
左
内
左
内
同
内
同旁内角
a
b
c
1
2
3
4
5
8
7
6
同位角
内错角
同旁内角
名称
内错角
同旁内角
同位角
位置特征
在截线的两侧,
被截直线的内侧
在截线的同侧,
被截直线的内侧
图示
a
b
c
F
1
2
3
4
5
8
7
6
在截线的同侧,
被截直线的同侧
每一对角的顶点不重合,顶点和其中的一条边
都在截线上,另一条边在被截直线上.
a
b
1
2
3
4
5
8
7
6
c
同位角:
∠1和∠5
∠4和∠8
∠2和∠6
∠3和∠7
∠9和∠4
找出下图中所有的同位角:
9
∠9和∠5
a
b
1
2
3
4
5
8
7
6
c
9
内错角:
∠3和∠5
∠4和∠6
∠9和∠2
找出下图中所有的内错角:
∠9和∠7
a
b
1
2
3
4
5
8
7
6
c
9
同旁内角:
∠3和∠6
∠4和∠5
∠9和∠3
找出下图中所有的同旁内角:
∠9和∠6
10
9
12
11
a
b
1
2
3
4
5
7
6
8
找出下图中所有的同位角、内错角
同旁内角:
2
判断:下列图形中,∠1和∠2是否是同位角?
1
2
1
2
1
1
2
1
2
注意:
同位角、内错角、同
旁内角存在的前提:三
线.
图形比较复杂时,应
当分解图形,一般留下
要用的“三线”.
×
√
√
√
√
选择:下面四个图形中,∠1和∠2不是内错
角的是(
)
1
2
2
1
1
2
1
2
(A)
(B)
(C)
(D)
A
A
B
C
D
1
2
3
4
5
6
7
在∠1、∠2、∠3、∠4、∠5、∠6、∠7中,
(1)哪些是直线DC和AB被直线AC所截得的内错角?
(2)哪些是直线AD和BC被直线AC所截得的内错角?
(3)哪些是直线DC和AC被直线AD所截得的同位角?
(4)哪些是直线AC和AB被直线BC所截得的同旁内角?
A
B
C
E
D
1
2
4
3
2
1
3
4
A
B
C
D
A
B
C
E
F
1
2
3
4
判断:图中∠1和∠2
、∠3和∠4各是哪两条直线被哪一条直线所截而成?它们各是什么角?
证明:
∵∠1=∠4(已知)
∠4+∠3=180度(邻补角的意义)
∴∠1+∠3=180度(等量代换)
∴∠1和∠3互补(互补的意义)
例:如图,直线DE、BC被直线AB所截.
(1)∠1与∠2、∠1与∠3、∠1与∠4各是
什么角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?
1
4
2
3
A
B
C
D
E
证明:
∵
∠1=∠4(已知)
∠2=∠4(对顶角相等)
∴
∠1=∠2(等量代换)
小结:
1、三线八角中,有四对同位角,两对内错角,
两对同旁内角.
2、要抓住八角的位置特征,分清楚是哪两条
直线被第三条直线所截
.
3、当图形复杂时,要学会画分解图形.
