13.4 平行线的判定(1) 课件(14张PPT)
文档属性
| 名称 | 13.4 平行线的判定(1) 课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 421.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 08:40:47 | ||
图片预览






文档简介
(共14张PPT)
一、创设情境,引入课题
生活中到处可见平行线的形象,
你能举出在周围所看到的形象
为平行线的例子吗?
平行线概念:
同一平面内不相交
的两条直线叫做平行线.
“平行”用符号“∥”表示.
如图:直线
和
是平行线,
也称它们互相平行,
在同一平面内,两条不重合的直线位置关系是:
平行或相交.
平面上两直线的位置关系
平行
相交
斜交
垂直
读作“
平行于
”.
记作“
∥
”,
在同一平面内不相交的两条直线是平行线
由于直线是向两方无限延伸的
,我们看到的
只是直线的一部分,因此要用“不相交”去判定两条直线平行是十分困难的。
为此我们要寻找一些判定两直线平行方法,
学行线的判定
你有办法测定两条直线是平行线吗?
二、探究新知
操作
已知直线
,请用直尺和
三角尺画一条直线
,使
与
平行。
三线八角图
画已知直线的平行线的步骤:
一叠、(把三角尺叠放在已知直线上)
二靠、(把直尺靠住三角尺)
三移、(三角尺贴住直尺平移)
四画、(画出与已知直线平行的直线)
演示
在平行线的操作过程中,三角尺起什么作用?
二、探究新知
操作
已知直线
,请用直尺和
三角尺画一条直线
,使
与
平行。
在三角尺平移的过程中,实质是具备了什么条件,才能确保直线
与
平行
三线八角图
画直线
时,只要保持同位角相等,那么画出的直线
就平行于直线
.
确保三线八角图中的同位角
、
大小相等
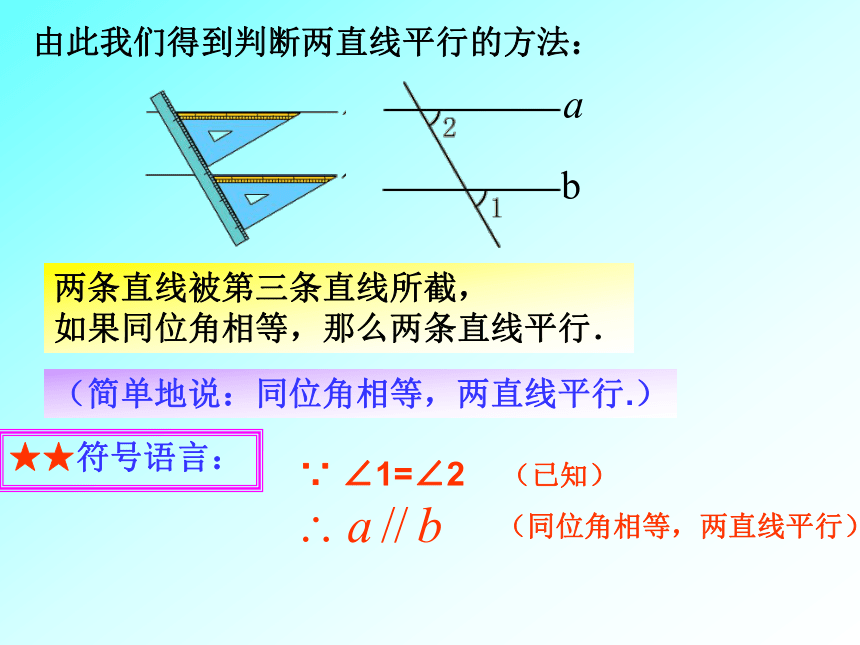
由此我们得到判断两直线平行的方法:
两条直线被第三条直线所截,
如果同位角相等,那么两条直线平行.
(简单地说:同位角相等,两直线平行.)
★★符号语言:
∵
∠1=∠2
(已知)
(同位角相等,两直线平行)
操作2:用平移三角尺的方法画出经过点
且平行于
的直线
.
巩固练习1
用平移三角尺的方法画经过点
且平行于
的直线
.
平行线基本性质:
过直线外一点有且只有
一条直线与已知直线平行.
过直线外一点画已知直线的平行线步骤:
一叠、二靠、三移(过点)、四画
如图,在同一个平面内,
,
说明
的理由.
90°
(垂直的意义).
同理
(垂直的意义).
得
∠1=∠2
(等量代换).
∴
∥
(同位角相等,两直线平行)
归纳为:在同一平面内,垂直于同一条直线的两条直线平行.
★★符号语言:
90°
找相等的同位角
∵
(已知)
三、例题
讲解
例题1
如图,直线L与直线a、b、c分别相交,且
∠1=∠2=∠3
.
(1)从∠1=∠2可以得出哪两条直线平行?为什么?
(2)从∠1=∠3可以得出哪两条直线平行?为什么?
(1)答:
∥
解:∵
∠1=∠2(已知),
∴
∥ (同位角相等,两直线平行).
(2)答:
∥
解:
将∠1的对顶角记作∠4
则∠1=∠4(对顶角相等)
∵∠1=∠3(已知),
得∠3=∠4(等量代换)
∴
∥ (同位角相等,两直线平行).
∠1、∠2是什么位置关系的角?
∠1、∠3是同位角吗?
4
∠4、∠3是同位角吗?相等吗?
5
四、课堂练习P53
1、
答:
解:
将∠1的邻补角记作∠3
则
3
∠1+
∠3= 180°(邻补角的意义)
∵
∠1=110°
(
)
∴
∠3=
180°-
∠1=
180°-
110°(等式的性质)
又∵
∠2=70°
(
)
得∠2
∠3
(
)
∴AB//CD
(
同位角相等,两直线平行)
已知
已知
等量代换
=
要说明AB//CD,就要找到由AB、CD及一条截线构成的两个同位角相等.
3.如图:已知∠1=110°,∠2=70
°
那么AB//CD吗?为什么?
四、课堂练习P53
答:AB//CD
b
教师黑板演示
五、课堂小结
4、同一平面内,垂直于同一直线的两直线平行.
1.过直线外一点画已知直线的平行线;
过直线外一点画已知直线的平行线步骤:
一叠、二靠、三移(过点)、四画.
2、平行线判定方法1:
∵
∠1=∠2
(已知)
同位角相等,两直线平行.
3、平行线基本性质:
过直线外一点有且只有一条直线与已知直线平行.
(同位角相等,两直线平行)
一、创设情境,引入课题
生活中到处可见平行线的形象,
你能举出在周围所看到的形象
为平行线的例子吗?
平行线概念:
同一平面内不相交
的两条直线叫做平行线.
“平行”用符号“∥”表示.
如图:直线
和
是平行线,
也称它们互相平行,
在同一平面内,两条不重合的直线位置关系是:
平行或相交.
平面上两直线的位置关系
平行
相交
斜交
垂直
读作“
平行于
”.
记作“
∥
”,
在同一平面内不相交的两条直线是平行线
由于直线是向两方无限延伸的
,我们看到的
只是直线的一部分,因此要用“不相交”去判定两条直线平行是十分困难的。
为此我们要寻找一些判定两直线平行方法,
学行线的判定
你有办法测定两条直线是平行线吗?
二、探究新知
操作
已知直线
,请用直尺和
三角尺画一条直线
,使
与
平行。
三线八角图
画已知直线的平行线的步骤:
一叠、(把三角尺叠放在已知直线上)
二靠、(把直尺靠住三角尺)
三移、(三角尺贴住直尺平移)
四画、(画出与已知直线平行的直线)
演示
在平行线的操作过程中,三角尺起什么作用?
二、探究新知
操作
已知直线
,请用直尺和
三角尺画一条直线
,使
与
平行。
在三角尺平移的过程中,实质是具备了什么条件,才能确保直线
与
平行
三线八角图
画直线
时,只要保持同位角相等,那么画出的直线
就平行于直线
.
确保三线八角图中的同位角
、
大小相等
由此我们得到判断两直线平行的方法:
两条直线被第三条直线所截,
如果同位角相等,那么两条直线平行.
(简单地说:同位角相等,两直线平行.)
★★符号语言:
∵
∠1=∠2
(已知)
(同位角相等,两直线平行)
操作2:用平移三角尺的方法画出经过点
且平行于
的直线
.
巩固练习1
用平移三角尺的方法画经过点
且平行于
的直线
.
平行线基本性质:
过直线外一点有且只有
一条直线与已知直线平行.
过直线外一点画已知直线的平行线步骤:
一叠、二靠、三移(过点)、四画
如图,在同一个平面内,
,
说明
的理由.
90°
(垂直的意义).
同理
(垂直的意义).
得
∠1=∠2
(等量代换).
∴
∥
(同位角相等,两直线平行)
归纳为:在同一平面内,垂直于同一条直线的两条直线平行.
★★符号语言:
90°
找相等的同位角
∵
(已知)
三、例题
讲解
例题1
如图,直线L与直线a、b、c分别相交,且
∠1=∠2=∠3
.
(1)从∠1=∠2可以得出哪两条直线平行?为什么?
(2)从∠1=∠3可以得出哪两条直线平行?为什么?
(1)答:
∥
解:∵
∠1=∠2(已知),
∴
∥ (同位角相等,两直线平行).
(2)答:
∥
解:
将∠1的对顶角记作∠4
则∠1=∠4(对顶角相等)
∵∠1=∠3(已知),
得∠3=∠4(等量代换)
∴
∥ (同位角相等,两直线平行).
∠1、∠2是什么位置关系的角?
∠1、∠3是同位角吗?
4
∠4、∠3是同位角吗?相等吗?
5
四、课堂练习P53
1、
答:
解:
将∠1的邻补角记作∠3
则
3
∠1+
∠3= 180°(邻补角的意义)
∵
∠1=110°
(
)
∴
∠3=
180°-
∠1=
180°-
110°(等式的性质)
又∵
∠2=70°
(
)
得∠2
∠3
(
)
∴AB//CD
(
同位角相等,两直线平行)
已知
已知
等量代换
=
要说明AB//CD,就要找到由AB、CD及一条截线构成的两个同位角相等.
3.如图:已知∠1=110°,∠2=70
°
那么AB//CD吗?为什么?
四、课堂练习P53
答:AB//CD
b
教师黑板演示
五、课堂小结
4、同一平面内,垂直于同一直线的两直线平行.
1.过直线外一点画已知直线的平行线;
过直线外一点画已知直线的平行线步骤:
一叠、二靠、三移(过点)、四画.
2、平行线判定方法1:
∵
∠1=∠2
(已知)
同位角相等,两直线平行.
3、平行线基本性质:
过直线外一点有且只有一条直线与已知直线平行.
(同位角相等,两直线平行)
