13.4 平行线的判定(2) 课件(12张PPT)
文档属性
| 名称 | 13.4 平行线的判定(2) 课件(12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 08:40:47 | ||
图片预览





文档简介
(共12张PPT)
13.4
平行线的判定
(2)
回顾
&
思考
a
b
l
1
2
如图,已知∠1=∠2,
则直线a与直线b平行吗?
根据什么?
两条直线被第三条直线所截,如果同位角相等,
那么这两条直线平行。
探索新知
3
如图,直线a、b被直线l所截,∠1与∠2是内错角,
且∠1=∠2,那么直线a、b有怎样的位置关系
为什么?
a
b
l
2
1
两条直线被第三条直线所截,如果内错角相等,
那么这两条直线平行。
1、已知∠1=∠2,下列图形中,能够根据已知条件判定a//b吗?
不能
不能
能
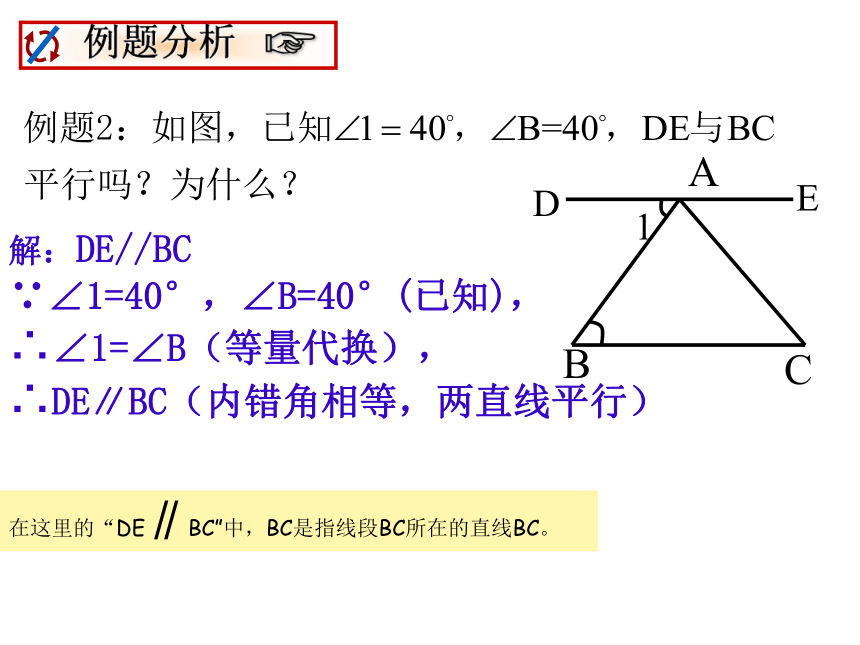
例题分析
A
B
C
1
D
E
∵∠1=40°,∠B=40°(已知),
∴∠1=∠B(等量代换),
∴DE∥BC(内错角相等,两直线平行)
在这里的“DE∥BC”中,BC是指线段BC所在的直线BC。
例题分析
解:DE//BC
探索新知
3
如图,直线a、b被直线l
所截,∠1与∠2是同旁内角,
如果∠1+∠2=180°,那么直线a、b的位置关系如何?
为什么?
a
b
l
2
1
两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行。
1
3
2
a
b
c
解:将∠1的对顶角记作∠3,
则∠1=∠3=60°(对顶角相等)
∵∠2=120°(已知)
∴∠2+∠3=120°+60°=180°(等式性质)
∴a∥b(同旁内角互补,两直线平行)
例题分析
例题分析
知识重温
平行线的判定方法:
1、同位角相等,两直线平行
2、内错角相等,两直线平行
3、同旁内角互补,两直线平行
(A)∠2=∠3
(B)∠1=∠4
(C)∠1=∠2
(D)∠1=∠3
1、如图,不能判定
的是(
)
伸展运动
D
⑴∵∠1=∠A,(已知)
∴
___
∥
___
,(
);
⑵∵∠3=∠B,
(已知)
∴
___
∥
___
,(
);
⑶∵∠2+∠A=180°,
(已知)
∴
___
∥
___
,
(
);
⑷∵∠1=∠4,
(已知)
∴
___
∥
___
,
(
);
⑸∵∠C+
___
=180°,
(已知)
∴
∥
,
(
);
⑹∵∠4=
___
,
(已知)
∴
EF
∥
AB
,
(
);
A
B
C
D
E
F
G
1
2
3
4
2、如图
全身运动
CG
EF
AB
CG
AB
CG
AB
EF
CG
AB
∠B
∠A
内错角相等
,两直线平行
同旁内角互补,两直线平行
同位角相等
,两直线平行
内错角相等
,两直线平行
同旁内角互补,两直线平行
同位角相等
,两直线平行
3、已知:AC⊥AB,BD⊥AB,∠CAE=∠DBF,试说明AE∥FB
解∵AC⊥AB,BD⊥AB(已知)
∴∠CAB=∠_____=90°(
)
∵∠CAE=∠DBF(已知)
∴∠CAB-∠_____=∠DBA-∠_____
(
)
即∠BAE=∠______
∴_____∥_____(
)
C
A
F
E
B
D
DBA
垂直的意义
CAE
DBF
等式的性质
ABF
AE
BF
内错角相等,
两直线平行
跳跃运动
通过这节课的学习,
你有哪些收获
13.4
平行线的判定
(2)
回顾
&
思考
a
b
l
1
2
如图,已知∠1=∠2,
则直线a与直线b平行吗?
根据什么?
两条直线被第三条直线所截,如果同位角相等,
那么这两条直线平行。
探索新知
3
如图,直线a、b被直线l所截,∠1与∠2是内错角,
且∠1=∠2,那么直线a、b有怎样的位置关系
为什么?
a
b
l
2
1
两条直线被第三条直线所截,如果内错角相等,
那么这两条直线平行。
1、已知∠1=∠2,下列图形中,能够根据已知条件判定a//b吗?
不能
不能
能
例题分析
A
B
C
1
D
E
∵∠1=40°,∠B=40°(已知),
∴∠1=∠B(等量代换),
∴DE∥BC(内错角相等,两直线平行)
在这里的“DE∥BC”中,BC是指线段BC所在的直线BC。
例题分析
解:DE//BC
探索新知
3
如图,直线a、b被直线l
所截,∠1与∠2是同旁内角,
如果∠1+∠2=180°,那么直线a、b的位置关系如何?
为什么?
a
b
l
2
1
两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行。
1
3
2
a
b
c
解:将∠1的对顶角记作∠3,
则∠1=∠3=60°(对顶角相等)
∵∠2=120°(已知)
∴∠2+∠3=120°+60°=180°(等式性质)
∴a∥b(同旁内角互补,两直线平行)
例题分析
例题分析
知识重温
平行线的判定方法:
1、同位角相等,两直线平行
2、内错角相等,两直线平行
3、同旁内角互补,两直线平行
(A)∠2=∠3
(B)∠1=∠4
(C)∠1=∠2
(D)∠1=∠3
1、如图,不能判定
的是(
)
伸展运动
D
⑴∵∠1=∠A,(已知)
∴
___
∥
___
,(
);
⑵∵∠3=∠B,
(已知)
∴
___
∥
___
,(
);
⑶∵∠2+∠A=180°,
(已知)
∴
___
∥
___
,
(
);
⑷∵∠1=∠4,
(已知)
∴
___
∥
___
,
(
);
⑸∵∠C+
___
=180°,
(已知)
∴
∥
,
(
);
⑹∵∠4=
___
,
(已知)
∴
EF
∥
AB
,
(
);
A
B
C
D
E
F
G
1
2
3
4
2、如图
全身运动
CG
EF
AB
CG
AB
CG
AB
EF
CG
AB
∠B
∠A
内错角相等
,两直线平行
同旁内角互补,两直线平行
同位角相等
,两直线平行
内错角相等
,两直线平行
同旁内角互补,两直线平行
同位角相等
,两直线平行
3、已知:AC⊥AB,BD⊥AB,∠CAE=∠DBF,试说明AE∥FB
解∵AC⊥AB,BD⊥AB(已知)
∴∠CAB=∠_____=90°(
)
∵∠CAE=∠DBF(已知)
∴∠CAB-∠_____=∠DBA-∠_____
(
)
即∠BAE=∠______
∴_____∥_____(
)
C
A
F
E
B
D
DBA
垂直的意义
CAE
DBF
等式的性质
ABF
AE
BF
内错角相等,
两直线平行
跳跃运动
通过这节课的学习,
你有哪些收获
