13.4 平行线的判定(2) 课件(14张PPT)
文档属性
| 名称 | 13.4 平行线的判定(2) 课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 31.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 08:40:47 | ||
图片预览






文档简介
(共14张PPT)
§13.4
(2)
复习引入
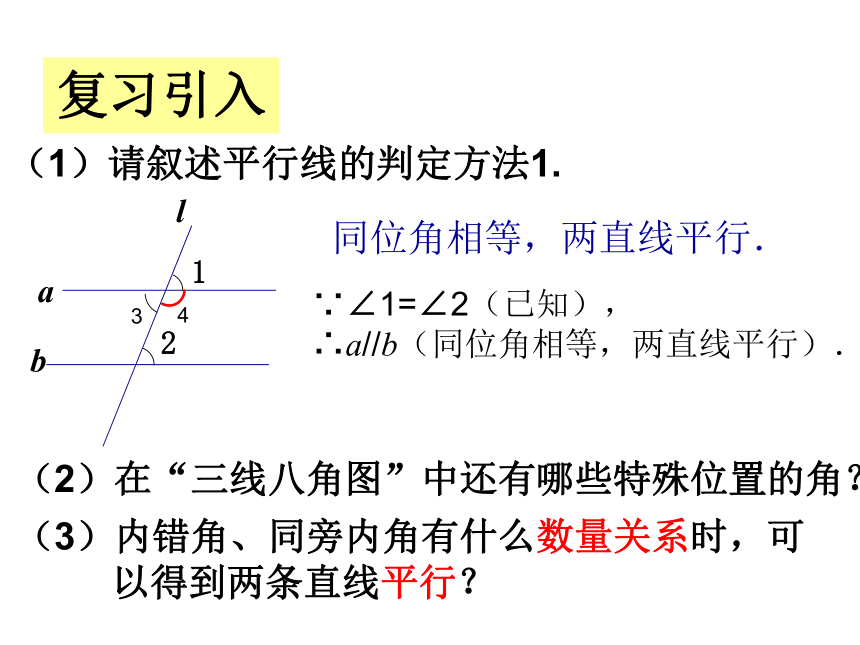
(1)请叙述平行线的判定方法1.
同位角相等,两直线平行.
l
b
a
∵∠1=∠2(已知),
∴a//b(同位角相等,两直线平行).
(2)在“三线八角图”中还有哪些特殊位置的角?
(3)内错角、同旁内角有什么数量关系时,可
以得到两条直线平行?
如何将这个新问题转化成我们已知的平行线判定方法呢?
探究新知,讲授新课
如图,直线a、b被直线l所截,∠1=∠2,直线a、b平行吗?为什么?
l
b
a
解
将∠1的对顶角记作∠3,
∴a//b(同位角相等,两直线平行).
∴∠2=∠3(等量代换),
∠1=∠3(对顶角相等),
∵∠1=∠2(已知),
答:平行.
请试着用文字语言叙述上述发现.
两直线平行.
内错角相等,
内错角相等
还有别的方法吗?
平行线的判定方法2
内错角相等,两直线平行.
l
b
a
∵∠1=∠2(已知),
∴a//b(内错角相等,两直线平行).
探究新知,讲授新课
同旁内角有什么数量关系时,可以得到两条直线平行?
内错角相等,两直线平行.
探究新知,讲授新课
同位角相等,两直线平行.
探究新知,讲授新课
如图,直线a、b被直线l所截,∠1+∠2=180°,直线a、b的平行吗?为什么?
解
将∠1的邻补角记作∠3,
∴a//b
(同位角相等,两直线平行).
∴∠2=∠3
(同角的补角相等),
∠1+∠2=180°
(已知),
∵∠1+∠3=180°(邻补角的意义),
答:平行.
同旁内角互补
如何将这个新问题转化成我们已知的平行线判定方法呢?
探究新知,讲授新课
如图,直线a、b被直线l所截,∠1+∠2=180°,直线a、b的平行吗?为什么?
解
将∠1的邻补角记作∠3,
∴a//b
(同位角相等,两直线平行).
∴∠2=∠3
(同角的补角相等),
∠1+∠2=180°
(已知),
∵∠1+∠3=180°(邻补角的意义),
答:平行.
同旁内角互补
还有别的转化方法吗?
解
将∠1的邻补角记作∠4,
∵∠1+∠4=180°(邻补角的意义),
∴∠4=∠2
(同角的补角相等),
∴a//b
(内错角相等,两直线平行).
请试着用文字语言叙述上述发现.
两直线平行.
同旁内角互补,
平行线的判定方法3
同旁内角互补,两直线平行.
∵∠1+∠2=180°(已知),
∴a//b(同旁内角互补,两直线平行).
探究新知,讲授新课
实践运用
例题1
如图,已知∠1=40°,∠B=40°,
DE与BC平行吗?为什么?
它们是什么位置关系的角
∴
DE//BC
(内错角相等,两直线平行).
∵∠1=∠B(等量代换),
解
∵∠1=40°,∠B=40°(已知),
答:平行.
它们有什么数量关系?
实践运用
例题2
如图,直线a、b被直线c所截,已知∠1=59°,∠2=121°,直线a与b平行吗?为什么?
∴
a//b(同旁内角互补,两直线平行).
∠2=121°(已知),
∵∠3=∠1=59°(对顶角相等),
答:平行.
它们是同旁内角吗?
解
将∠1的对顶角记作∠3,
∵∠2+∠3=180°(等式性质),
还有别的方法吗?
如何转化?
∠B
和∠3是什么位置关系的角?
课堂练习
1.填空:如图,
(1)∵∠B
=∠3(已
知),
∴
∥
(
).
同位角相等,两直线平行.
AB
CD
AD
BC
内错角相等,两直线平行.
(2)∵∠D
=∠3(已知),
∴
∥
(
).
课堂练习
1.填空:如图,
(3)∵∠B
+∠BCD=180°(已知),
∴
∥
(
).
AB
CD
同旁内角互补,两直线平行.
BCD
同旁内角互补,两直线平行.
2
内错角相等,两直线平行.
(4)∵∠D
+∠
=180°(已知),
∴AD∥BC(
).
(5)∵∠4
=∠
(已知),
∴AB∥CD(
).
它们是什么位置关系的角?
找哪两个角关系来解决问题?
课堂练习
2.如图,已知∠1=65°,∠2=∠3=115
°
,
那么AB
与CD平行吗?
EF
与GH平行吗 为什么?
解:将∠1的邻补角记作∠4,则
∠1+∠4=180
°(
),
∵
∠1=65
°(
),
∴
∠4=180°—
∠1
=180
°—65
°=115
°,
∵
∠2=115°(
)
∴
∠2=
∠4(
),
∴
_∥
_(
)
∵
∠4=115°,
∠3=115°,
∴∠3=
∠4(
),
∴
_
∥
_
(
)
1
2
3
如何转化?
邻补角的意义
已知
已知
等量代换
内错角相等,两直线平行
AB
CD
找哪两个角关系来解决问题?
等量代换
EF
GH
同位角相等,两直线平行
自主小结
同位角相等,两直线平行.
同旁内角互补,两直线平行.
内错角相等,两直线平行.
正确选择平行线的判定方法.
§13.4
(2)
复习引入
(1)请叙述平行线的判定方法1.
同位角相等,两直线平行.
l
b
a
∵∠1=∠2(已知),
∴a//b(同位角相等,两直线平行).
(2)在“三线八角图”中还有哪些特殊位置的角?
(3)内错角、同旁内角有什么数量关系时,可
以得到两条直线平行?
如何将这个新问题转化成我们已知的平行线判定方法呢?
探究新知,讲授新课
如图,直线a、b被直线l所截,∠1=∠2,直线a、b平行吗?为什么?
l
b
a
解
将∠1的对顶角记作∠3,
∴a//b(同位角相等,两直线平行).
∴∠2=∠3(等量代换),
∠1=∠3(对顶角相等),
∵∠1=∠2(已知),
答:平行.
请试着用文字语言叙述上述发现.
两直线平行.
内错角相等,
内错角相等
还有别的方法吗?
平行线的判定方法2
内错角相等,两直线平行.
l
b
a
∵∠1=∠2(已知),
∴a//b(内错角相等,两直线平行).
探究新知,讲授新课
同旁内角有什么数量关系时,可以得到两条直线平行?
内错角相等,两直线平行.
探究新知,讲授新课
同位角相等,两直线平行.
探究新知,讲授新课
如图,直线a、b被直线l所截,∠1+∠2=180°,直线a、b的平行吗?为什么?
解
将∠1的邻补角记作∠3,
∴a//b
(同位角相等,两直线平行).
∴∠2=∠3
(同角的补角相等),
∠1+∠2=180°
(已知),
∵∠1+∠3=180°(邻补角的意义),
答:平行.
同旁内角互补
如何将这个新问题转化成我们已知的平行线判定方法呢?
探究新知,讲授新课
如图,直线a、b被直线l所截,∠1+∠2=180°,直线a、b的平行吗?为什么?
解
将∠1的邻补角记作∠3,
∴a//b
(同位角相等,两直线平行).
∴∠2=∠3
(同角的补角相等),
∠1+∠2=180°
(已知),
∵∠1+∠3=180°(邻补角的意义),
答:平行.
同旁内角互补
还有别的转化方法吗?
解
将∠1的邻补角记作∠4,
∵∠1+∠4=180°(邻补角的意义),
∴∠4=∠2
(同角的补角相等),
∴a//b
(内错角相等,两直线平行).
请试着用文字语言叙述上述发现.
两直线平行.
同旁内角互补,
平行线的判定方法3
同旁内角互补,两直线平行.
∵∠1+∠2=180°(已知),
∴a//b(同旁内角互补,两直线平行).
探究新知,讲授新课
实践运用
例题1
如图,已知∠1=40°,∠B=40°,
DE与BC平行吗?为什么?
它们是什么位置关系的角
∴
DE//BC
(内错角相等,两直线平行).
∵∠1=∠B(等量代换),
解
∵∠1=40°,∠B=40°(已知),
答:平行.
它们有什么数量关系?
实践运用
例题2
如图,直线a、b被直线c所截,已知∠1=59°,∠2=121°,直线a与b平行吗?为什么?
∴
a//b(同旁内角互补,两直线平行).
∠2=121°(已知),
∵∠3=∠1=59°(对顶角相等),
答:平行.
它们是同旁内角吗?
解
将∠1的对顶角记作∠3,
∵∠2+∠3=180°(等式性质),
还有别的方法吗?
如何转化?
∠B
和∠3是什么位置关系的角?
课堂练习
1.填空:如图,
(1)∵∠B
=∠3(已
知),
∴
∥
(
).
同位角相等,两直线平行.
AB
CD
AD
BC
内错角相等,两直线平行.
(2)∵∠D
=∠3(已知),
∴
∥
(
).
课堂练习
1.填空:如图,
(3)∵∠B
+∠BCD=180°(已知),
∴
∥
(
).
AB
CD
同旁内角互补,两直线平行.
BCD
同旁内角互补,两直线平行.
2
内错角相等,两直线平行.
(4)∵∠D
+∠
=180°(已知),
∴AD∥BC(
).
(5)∵∠4
=∠
(已知),
∴AB∥CD(
).
它们是什么位置关系的角?
找哪两个角关系来解决问题?
课堂练习
2.如图,已知∠1=65°,∠2=∠3=115
°
,
那么AB
与CD平行吗?
EF
与GH平行吗 为什么?
解:将∠1的邻补角记作∠4,则
∠1+∠4=180
°(
),
∵
∠1=65
°(
),
∴
∠4=180°—
∠1
=180
°—65
°=115
°,
∵
∠2=115°(
)
∴
∠2=
∠4(
),
∴
_∥
_(
)
∵
∠4=115°,
∠3=115°,
∴∠3=
∠4(
),
∴
_
∥
_
(
)
1
2
3
如何转化?
邻补角的意义
已知
已知
等量代换
内错角相等,两直线平行
AB
CD
找哪两个角关系来解决问题?
等量代换
EF
GH
同位角相等,两直线平行
自主小结
同位角相等,两直线平行.
同旁内角互补,两直线平行.
内错角相等,两直线平行.
正确选择平行线的判定方法.
