高中数学必修5第一章解三角形1.1.2余弦定理(共33张PPT)
文档属性
| 名称 | 高中数学必修5第一章解三角形1.1.2余弦定理(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 451.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-08 00:00:00 | ||
图片预览








文档简介
(共33张PPT)
1.1.2 余弦定理
新课导入
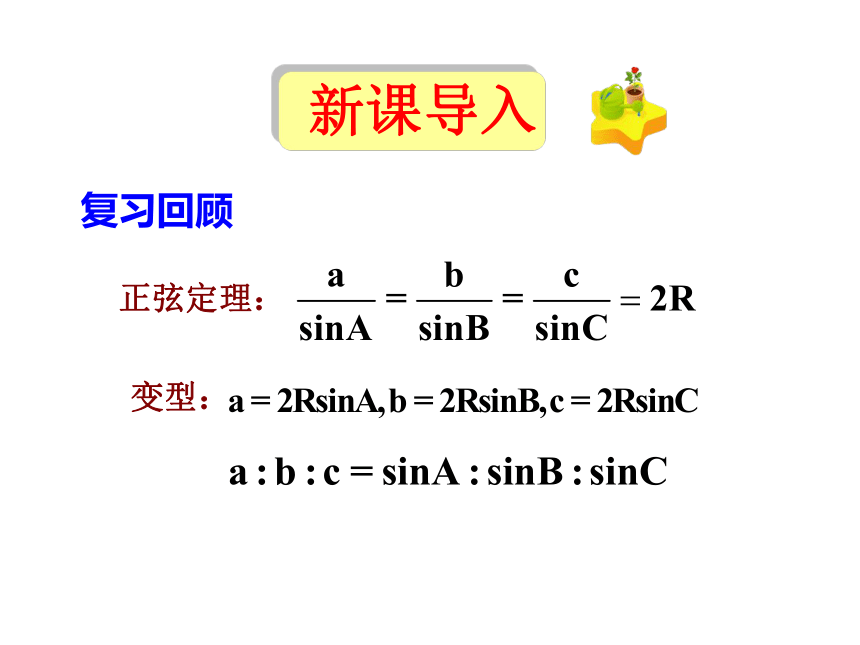
复习回顾
正弦定理:
变型:
探究
如果已知一个三角形的两条边及其所夹的角,根据三角形全等的判定方法,此三角形是大小、形状完全确定的三角形.
仍然从量化的角度来研究这个问题,已知两个边和它们的夹角,如何计算出三角形的另外一边和另外两个角的问题?
b
a
C
A
B
c
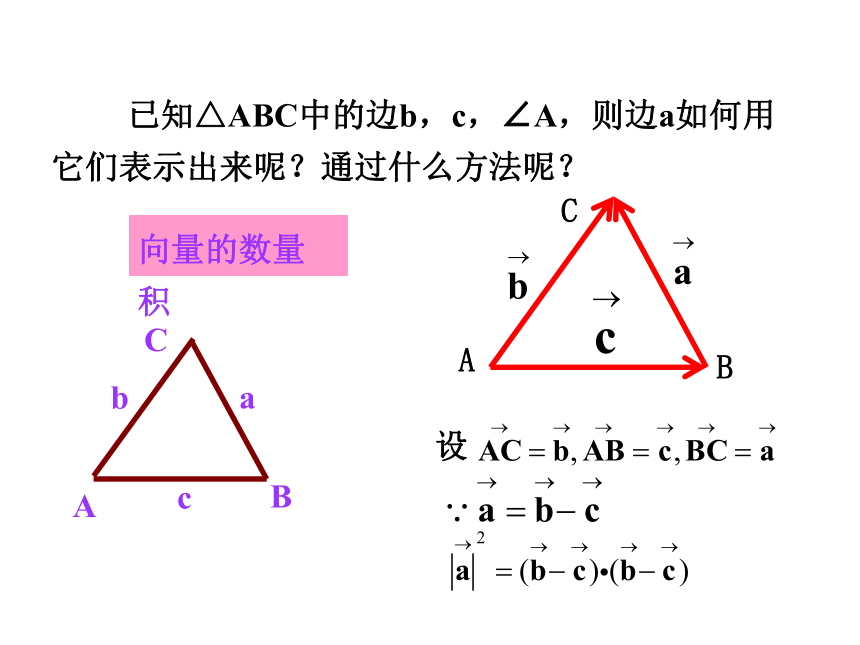
已知△ABC中的边b,c,∠A,则边a如何用它们表示出来呢?通过什么方法呢?
向量的数量积
C
A
B
设
同理可得
余弦定理
注:当A=90?时,此结论即为勾股定理.
知识要点
余弦定理(law of cosines)
三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们夹角余弦的积得两倍.即
能否把式子 转化为角的关系式?
思考
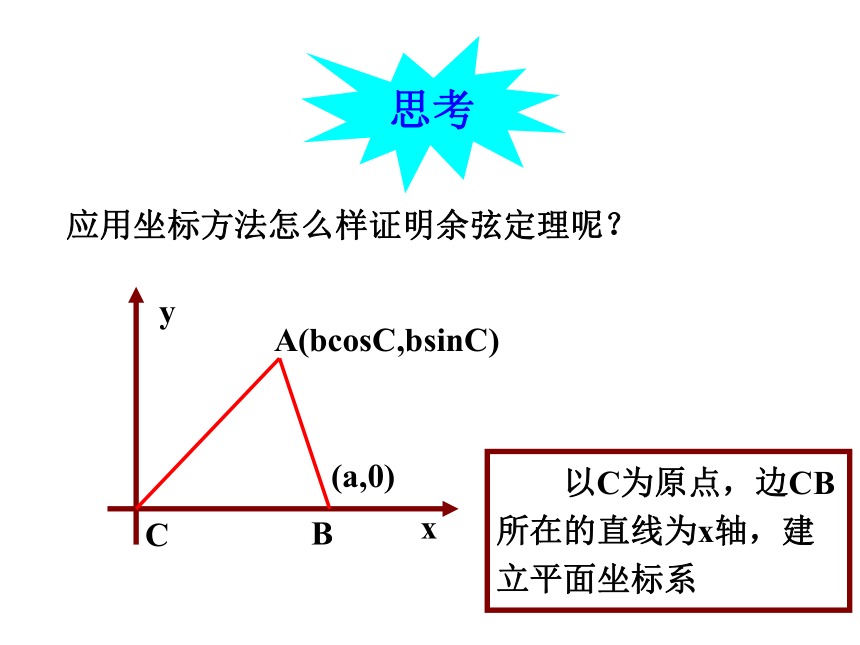
应用坐标方法怎么样证明余弦定理呢?
x
y
C
B
A(bcosC,bsinC)
以C为原点,边CB所在的直线为x轴,建立平面坐标系
(a,0)
根据两点距离公式:
整理得
同理可证明
还有其他方法吗?想一想吧!动手试一试吧!
A
B
C
a
b
c
D
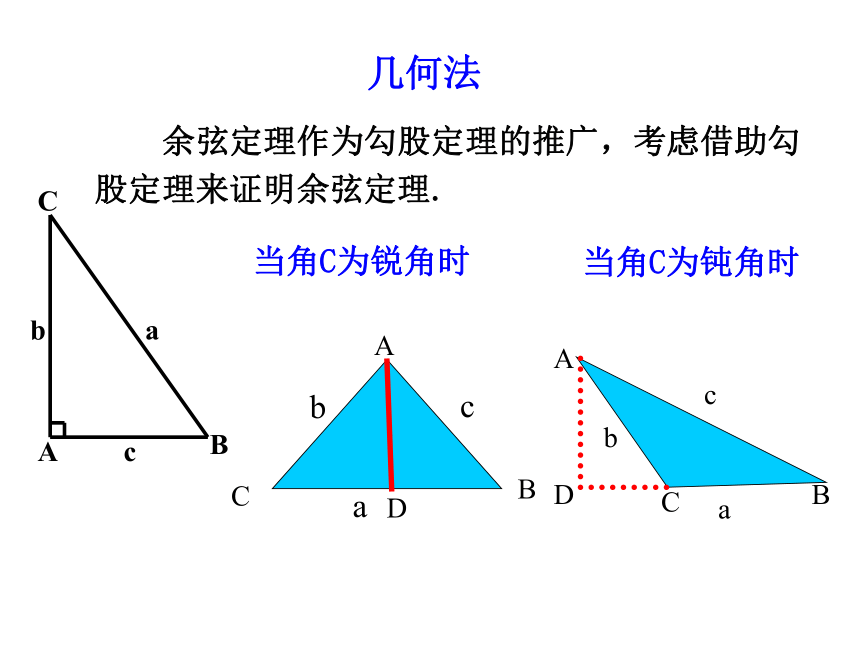
当角C为锐角时
几何法
b
A
a
c
C
B
D
当角C为钝角时
C
B
A
a
b
c
余弦定理作为勾股定理的推广,考虑借助勾股定理来证明余弦定理.
证明:在三角形ABC中,已知AB=c,AC=b和A, 作CD⊥AB,则CD=bsinA,BD=c-bcosA
A
B
C
c
b
a
同理有:
D
当然,对于钝角三角形来说,证明类似,课后 自己完成.
余弦定理的变形:
注意:余弦定理适用直角三角形吗?
C=90°
a2+b2=c2
注意:余弦定理适用任何角三角形.
余弦定理的用途:
(1)已知三边,求三个角;
(3)判断三角形的形状.
(2)已知两边和它们的夹角,求第三边和
其它两角;
例 1 在?ABC中,已知a=2.730,b=3.696,C=82°28′,解这个三角形.(边长保留四个有效数字,角度精确到1′)
解:由 c2=a2+b2-2abcosC,得 c≈4.297.
b2+c2-a2
2bc
∵ cosA= ≈0.7767,
∴ A≈39°2′,
∴ B=180°-(A+C)=58°30′.
a sinC
c
∵sinA= ≈0.6299,
∴ A=39°或141°(舍).
(
)
在解三角形时有时候用到余弦定理,有时候用到正弦定理,这两种方法有什么利弊吗?
1.已知两边和其中一边所对的角时,用正弦定理求另一边所对的角,应用内角和定理求第三个角,在用正弦定理求第三边;
2.已知两个角与其中一角所对的边时,先用内角和定理求第三角,再用正弦定理求边;
3.已知两边和它们的夹角时,用余弦定理求第三边;
4.已知三边时,应用余弦定理求出一个角,把问题转化为前面的类型.
例2 已知△ABC的三边为 、2、1,求它的最大内角.
解:不妨设三角形的三边分别a= ,b=2,c=1
则最大内角为∠A,
由余弦定理
得到
例3 在三角形ABC中,已知a=7,b=10,c=6,判定三角形ABC的形状.
分析:三角形ABC的形状是由大边b所对的大
角B决定的.
解:由余弦定理
得到
所以说三角形是钝角三角形.
分析:根据此式子
解:如图,在△ABC中由余弦定理得:
A
例6 我舰在敌岛A南偏西50°相距12海里的B处,发现敌舰正由岛沿北偏西10°的方向以10海里/小时的速度航行.问我舰需以多大速度、沿什么方向航行才能用2小时追上敌舰?
C
B
又在△ABC中由正弦定理得:
故我舰行的方向为北偏东
∴我舰的追击速度为14n mile/h
课堂小结
1.余弦定理(law of cosines)
三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们夹角余弦的积得两倍.即
2.余弦定理的变形:
3.余弦定理的用途:
(1)已知三边,求三个角;
(3)判断三角形的形状.
(2)已知两边和它们的夹角,求第三边和
其它两角;
高考链接
1.(18陕西)△ABC的内角A,B,C的对边分
别为a,b,c,若c= ,B=120°,则a
等于( )
D
【解析】由余弦定理,有
,得 ,
解得 ,故D.
2.(17湖南)△ABC的内角A,B,C的
对边分别为a,b。C,若a=1,b=
,c= ,则B=( )
C
【解析】将数据代入
,得 ,∴ .
3.(18宁夏)如果等腰三角形的周长是底
边长的5倍,那么它的顶角的余弦值为
( )
【解析】设等腰三角形的底边为a,顶
角为 ,则腰长为2a,由余弦定理得,
,故选D.
A. B. C. D.
D
课堂练习
1. 在△ABC中,已知B=30°,b=50 ,c=150,那么这个三角形是( )
A 等边三角形?B 直角三角形?
C 等腰三角形? D 等腰三角形或直角三角形
2.在△ABC中,角A、B均为锐角且cosA>sinB,则△ABC是
钝角三角形
D
解:利用余弦定理可知:
4.是△ABC中的最小角,且
则实数a的取值范围是 ( )
A. a≥3 B. a>-1
C. -1<a≤3 D. a>0
A
5.在△ABC中,若
则∠A=( )
B.
C.
D.
A.
C
6.在△ABC中,
,cosC是方程
的一个根,求△ABC周长
的最小值.
解:
又
是方程
的一个根
由余弦定理可得:
则:
当
时,c最小且
此时
△ABC周长的最小值为
再见
1.1.2 余弦定理
新课导入
复习回顾
正弦定理:
变型:
探究
如果已知一个三角形的两条边及其所夹的角,根据三角形全等的判定方法,此三角形是大小、形状完全确定的三角形.
仍然从量化的角度来研究这个问题,已知两个边和它们的夹角,如何计算出三角形的另外一边和另外两个角的问题?
b
a
C
A
B
c
已知△ABC中的边b,c,∠A,则边a如何用它们表示出来呢?通过什么方法呢?
向量的数量积
C
A
B
设
同理可得
余弦定理
注:当A=90?时,此结论即为勾股定理.
知识要点
余弦定理(law of cosines)
三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们夹角余弦的积得两倍.即
能否把式子 转化为角的关系式?
思考
应用坐标方法怎么样证明余弦定理呢?
x
y
C
B
A(bcosC,bsinC)
以C为原点,边CB所在的直线为x轴,建立平面坐标系
(a,0)
根据两点距离公式:
整理得
同理可证明
还有其他方法吗?想一想吧!动手试一试吧!
A
B
C
a
b
c
D
当角C为锐角时
几何法
b
A
a
c
C
B
D
当角C为钝角时
C
B
A
a
b
c
余弦定理作为勾股定理的推广,考虑借助勾股定理来证明余弦定理.
证明:在三角形ABC中,已知AB=c,AC=b和A, 作CD⊥AB,则CD=bsinA,BD=c-bcosA
A
B
C
c
b
a
同理有:
D
当然,对于钝角三角形来说,证明类似,课后 自己完成.
余弦定理的变形:
注意:余弦定理适用直角三角形吗?
C=90°
a2+b2=c2
注意:余弦定理适用任何角三角形.
余弦定理的用途:
(1)已知三边,求三个角;
(3)判断三角形的形状.
(2)已知两边和它们的夹角,求第三边和
其它两角;
例 1 在?ABC中,已知a=2.730,b=3.696,C=82°28′,解这个三角形.(边长保留四个有效数字,角度精确到1′)
解:由 c2=a2+b2-2abcosC,得 c≈4.297.
b2+c2-a2
2bc
∵ cosA= ≈0.7767,
∴ A≈39°2′,
∴ B=180°-(A+C)=58°30′.
a sinC
c
∵sinA= ≈0.6299,
∴ A=39°或141°(舍).
(
)
在解三角形时有时候用到余弦定理,有时候用到正弦定理,这两种方法有什么利弊吗?
1.已知两边和其中一边所对的角时,用正弦定理求另一边所对的角,应用内角和定理求第三个角,在用正弦定理求第三边;
2.已知两个角与其中一角所对的边时,先用内角和定理求第三角,再用正弦定理求边;
3.已知两边和它们的夹角时,用余弦定理求第三边;
4.已知三边时,应用余弦定理求出一个角,把问题转化为前面的类型.
例2 已知△ABC的三边为 、2、1,求它的最大内角.
解:不妨设三角形的三边分别a= ,b=2,c=1
则最大内角为∠A,
由余弦定理
得到
例3 在三角形ABC中,已知a=7,b=10,c=6,判定三角形ABC的形状.
分析:三角形ABC的形状是由大边b所对的大
角B决定的.
解:由余弦定理
得到
所以说三角形是钝角三角形.
分析:根据此式子
解:如图,在△ABC中由余弦定理得:
A
例6 我舰在敌岛A南偏西50°相距12海里的B处,发现敌舰正由岛沿北偏西10°的方向以10海里/小时的速度航行.问我舰需以多大速度、沿什么方向航行才能用2小时追上敌舰?
C
B
又在△ABC中由正弦定理得:
故我舰行的方向为北偏东
∴我舰的追击速度为14n mile/h
课堂小结
1.余弦定理(law of cosines)
三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们夹角余弦的积得两倍.即
2.余弦定理的变形:
3.余弦定理的用途:
(1)已知三边,求三个角;
(3)判断三角形的形状.
(2)已知两边和它们的夹角,求第三边和
其它两角;
高考链接
1.(18陕西)△ABC的内角A,B,C的对边分
别为a,b,c,若c= ,B=120°,则a
等于( )
D
【解析】由余弦定理,有
,得 ,
解得 ,故D.
2.(17湖南)△ABC的内角A,B,C的
对边分别为a,b。C,若a=1,b=
,c= ,则B=( )
C
【解析】将数据代入
,得 ,∴ .
3.(18宁夏)如果等腰三角形的周长是底
边长的5倍,那么它的顶角的余弦值为
( )
【解析】设等腰三角形的底边为a,顶
角为 ,则腰长为2a,由余弦定理得,
,故选D.
A. B. C. D.
D
课堂练习
1. 在△ABC中,已知B=30°,b=50 ,c=150,那么这个三角形是( )
A 等边三角形?B 直角三角形?
C 等腰三角形? D 等腰三角形或直角三角形
2.在△ABC中,角A、B均为锐角且cosA>sinB,则△ABC是
钝角三角形
D
解:利用余弦定理可知:
4.是△ABC中的最小角,且
则实数a的取值范围是 ( )
A. a≥3 B. a>-1
C. -1<a≤3 D. a>0
A
5.在△ABC中,若
则∠A=( )
B.
C.
D.
A.
C
6.在△ABC中,
,cosC是方程
的一个根,求△ABC周长
的最小值.
解:
又
是方程
的一个根
由余弦定理可得:
则:
当
时,c最小且
此时
△ABC周长的最小值为
再见
