2020春湘教版八年级下册数学习题课件:专题训练——平面直角坐标系中的有关计算(图片版,共23张PPT)
文档属性
| 名称 | 2020春湘教版八年级下册数学习题课件:专题训练——平面直角坐标系中的有关计算(图片版,共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-08 21:57:10 | ||
图片预览








文档简介
(共38张PPT)
★★
作业
课列
HUBEI
HONGHUZHII
教育梦
CULTURE
AND MEDIA
COLTD
鸿鹊志
十年奶一日专注教辅研发
发展潜能启诅智慧造就英才
专注教辅不断创新追求卓越
湖北鸿鹄志文化传媒有限公司
鸿鹄志文化
测控空
发展潜能启迪智慧造就英才
专注教辅不断创新追求卓越
3一本授学习方法的书
义务教育教科书(湘教版)八年级数学/下册
口你平
鸿韵志文化
专题训练(五)平面直角坐标系中的有关计算
专题概迹
平面直角坐标系中的计算题,往往涉及到求点的
坐标、求线段长、求图形的面积,解题时应结合图形
借助勾股定理,准确切入求解.
←专题突破
类型一求点的坐标
1.已知点A(2,7),AB∥x轴,AB=3,则点B的坐标
为
A.(5,7)
B.(2,10)
C.(2,10)或(2,4)
D.(5,7)或(-1,7)
2.如图,四边形ABCD是长方形,AB=3,AD=4.已
知A
1),则点C的坐标是
B
C.(3
332
3232
33
(
B
3.如图,在平面直角坐标系中,已知A(1,0),B(-1,
2),C(2,-2)三点坐标,若以A,B,C,D为顶点
的四边形是平行四边形,则点D的坐标可以
是(-2,0)或(0,-4)或(4,0)
X
T
4.(2019春·路北期中)已知点P(2m+4,m-1).试
分别根据下列条件,求出点P的坐标
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
(4)点P在过点A(2,-3),且与x轴平行的直
线上
解:(1)令2m+4=0,解得m=-2.∴点P的坐标
为(0,-3);
(2)令m-1=0,解得m=1.∴点P的坐标为(6,0);
(3)令m-1=(2m+4)+3,解得m=-8
点P的坐标为(-12,—9);
(4)令m-1=-3,解得m=-2.∴点P的坐标为
(0,-3)
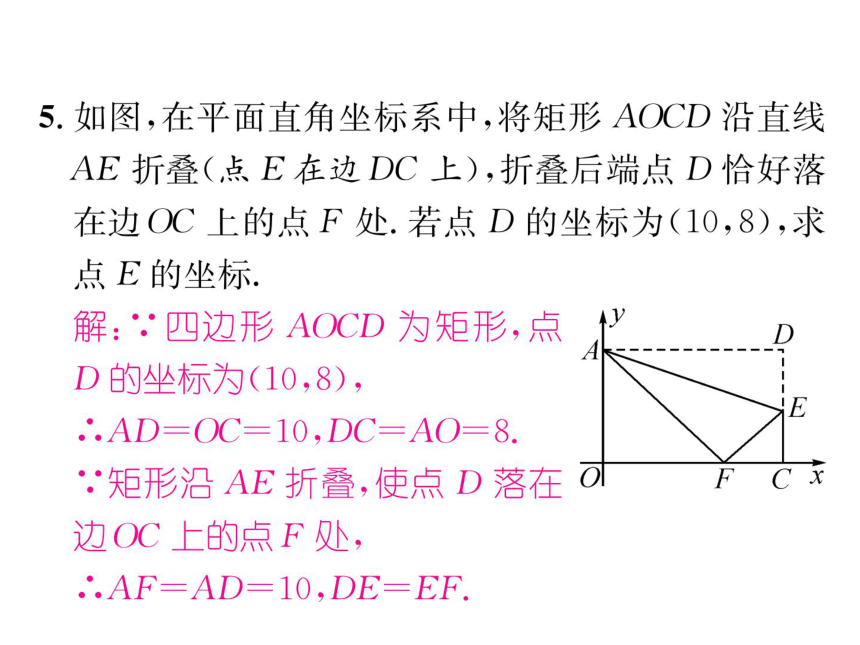
5.如图,在平面直角坐标系中,将矩形AOCD沿直线
AE折叠(点E在边DC上),折叠后端点D恰好落
在边OC上的点F处.若点D的坐标为(10,8),求
点E的坐标
解:∵四边形AOCD为矩形,点↑
D
D的坐标为(10,8),
E
∴AD=OC=10,DC=AO=8
∵矩形沿AE折叠,使点D落在O
F x
边OC上的点F处,
∴AF=AD=10,DE=EF
在Rt△AOF中,OF=√AF2=AOP=6,
FC=10-6=4
设EC=x,则DE=EF=8-x
在Rt△CEF中,EF2=EC2+FC2,
即(8-x)2=x2+42,解得x=3,
∴EC的长为3,点E的坐标为(10,3)
★★
作业
课列
HUBEI
HONGHUZHII
教育梦
CULTURE
AND MEDIA
COLTD
鸿鹊志
十年奶一日专注教辅研发
发展潜能启诅智慧造就英才
专注教辅不断创新追求卓越
湖北鸿鹄志文化传媒有限公司
鸿鹄志文化
测控空
发展潜能启迪智慧造就英才
专注教辅不断创新追求卓越
3一本授学习方法的书
义务教育教科书(湘教版)八年级数学/下册
口你平
鸿韵志文化
专题训练(五)平面直角坐标系中的有关计算
专题概迹
平面直角坐标系中的计算题,往往涉及到求点的
坐标、求线段长、求图形的面积,解题时应结合图形
借助勾股定理,准确切入求解.
←专题突破
类型一求点的坐标
1.已知点A(2,7),AB∥x轴,AB=3,则点B的坐标
为
A.(5,7)
B.(2,10)
C.(2,10)或(2,4)
D.(5,7)或(-1,7)
2.如图,四边形ABCD是长方形,AB=3,AD=4.已
知A
1),则点C的坐标是
B
C.(3
332
3232
33
(
B
3.如图,在平面直角坐标系中,已知A(1,0),B(-1,
2),C(2,-2)三点坐标,若以A,B,C,D为顶点
的四边形是平行四边形,则点D的坐标可以
是(-2,0)或(0,-4)或(4,0)
X
T
4.(2019春·路北期中)已知点P(2m+4,m-1).试
分别根据下列条件,求出点P的坐标
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
(4)点P在过点A(2,-3),且与x轴平行的直
线上
解:(1)令2m+4=0,解得m=-2.∴点P的坐标
为(0,-3);
(2)令m-1=0,解得m=1.∴点P的坐标为(6,0);
(3)令m-1=(2m+4)+3,解得m=-8
点P的坐标为(-12,—9);
(4)令m-1=-3,解得m=-2.∴点P的坐标为
(0,-3)
5.如图,在平面直角坐标系中,将矩形AOCD沿直线
AE折叠(点E在边DC上),折叠后端点D恰好落
在边OC上的点F处.若点D的坐标为(10,8),求
点E的坐标
解:∵四边形AOCD为矩形,点↑
D
D的坐标为(10,8),
E
∴AD=OC=10,DC=AO=8
∵矩形沿AE折叠,使点D落在O
F x
边OC上的点F处,
∴AF=AD=10,DE=EF
在Rt△AOF中,OF=√AF2=AOP=6,
FC=10-6=4
设EC=x,则DE=EF=8-x
在Rt△CEF中,EF2=EC2+FC2,
即(8-x)2=x2+42,解得x=3,
∴EC的长为3,点E的坐标为(10,3)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
