人教版八年级上册第十二章 12.3角平分线的性质 同步练习(含答案)
文档属性
| 名称 | 人教版八年级上册第十二章 12.3角平分线的性质 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 154.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-08 00:00:00 | ||
图片预览

文档简介
《角平分线》测试题
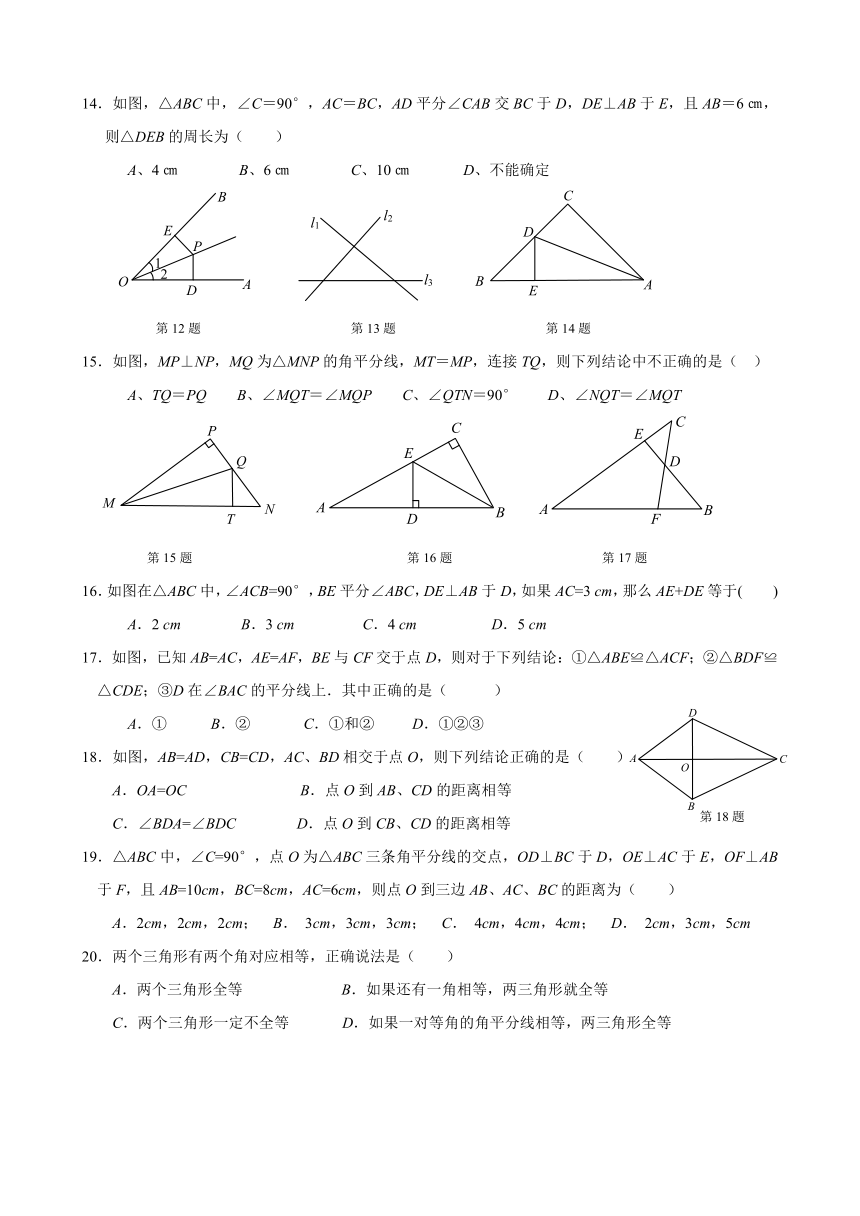
一、填空题(每小题3分,共30分)
1.已知:△ABC中,∠B=90°, ∠A、∠C的平分线交于点O,则∠AOC的度数为 .
2.角平分线上的点到_________________距离相等;到一个角的两边距离相等的点都在_____________.
3.∠AOB的平分线上一点M ,M到 OA的距离为1.5 cm,则M到OB的距离为_________.
4.如图,∠AOB=60°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=_________.
5.如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且DE=3 cm,BD=5 cm,则BC=_____cm.
6.如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、CB于点E、F,FG⊥AB,垂足为G,则CF______FG,CE________CF.
7.如图,已知AB、CD相交于点E,∠AEC及∠AED的平分线所在的直线为PQ与MN,则直线MN与PQ的关系是_________.
8.三角形的三条角平分线相交于一点,并且这一点到____________________相等.
9.点O是△ABC内一点,且点O到三边的距离相等,∠A=60°,则∠BOC的度数为_____________.
10.在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32cm,且BD∶CD=9∶7,则D到AB的距离为__________cm.
二、选择题(每小题3分,共30分)
11.三角形中到三边距离相等的点是( )
A、三条边的垂直平分线的交点 B、三条高的交点
C、三条中线的交点 D、三条角平分线的交点
12.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
A、PD=PE B、OD=OE C、∠DPO=∠EPO D、PD=OD
13.如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A、4处 B、3处 C、2处 D、1处
14.如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6㎝,则△DEB的周长为( )
A、4㎝ B、6㎝ C、10㎝ D、不能确定
第12题 第13题 第14题
15.如图,MP⊥NP,MQ为△MNP的角平分线,MT=MP,连接TQ,则下列结论中不正确的是( )
A、TQ=PQ B、∠MQT=∠MQP C、∠QTN=90° D、∠NQT=∠MQT
第15题 第16题 第17题
16.如图在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3 cm,那么AE+DE等于( )
A.2 cm B.3 cm C.4 cm D.5 cm
17.如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
A.① B.② C.①和② D.①②③
18.如图,AB=AD,CB=CD,AC、BD相交于点O,则下列结论正确的是( )
A.OA=OC B.点O到AB、CD的距离相等
C.∠BDA=∠BDC D.点O到CB、CD的距离相等
19.△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( )
A.2cm,2cm,2cm; B. 3cm,3cm,3cm; C. 4cm,4cm,4cm; D. 2cm,3cm,5cm
20.两个三角形有两个角对应相等,正确说法是( )
A.两个三角形全等 B.如果还有一角相等,两三角形就全等
C.两个三角形一定不全等 D.如果一对等角的角平分线相等,两三角形全等
三、解答与证明(共40分)
21.(6分)如图,已知OE、OD分别平分∠AOB和∠BOC,若∠AOB=90°,∠EOD=70°,求∠BOC的度数.
22.(6分)如图,已知△ABC中,AB=AC,D是BC的中点,求证:D到AB、AC的距离相等.
23.(7分)如图,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BD=CD.求证:AD平分∠BAC.
24.(7分)如图,已知BE平分∠ABC,CE平分∠ACD,且交BE于E.求证:AE平分∠FAC.
25.(7分)如图,已知AB=AC,AD=AE,DB与CE相交于O. (1)若DB⊥AC于D,CE⊥AB于E,试判断OE与OD的大小关系.并证明你的结论. (2)若没有第(1)中的条件,是否有这样的结论?试说明理由.
26.(7分)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:AM平分∠DAB.
《角平分线》测试题·答案
一、填空题
1、135°; 2、角的两边,这个角的平分线上; 3、1.5cm; 4、30° 5、8; 6、=,=;
7、PQ⊥MN; 8、三条边的距离; 9、120°; 10、14.
二、选择题:D D A B D ,B D D A D
三、解答题
21、50°;
22、证明:连AD,则可证△ABD≌△ACD(SSS),∴∠BAD=∠CAD,∴点D到AB、AC的距离相等.
23、简证:可得△BDF≌△CDE(AAS),∴DF=DE,又DF⊥AB,DE⊥AC,∴AD平分∠BAC.
24、简证:分别过E作EG⊥BD于G,EH⊥BF于H,EK⊥AC于K.∵BE平分∠ABC,CE平分∠ACD,∴EG=EH,EG=EK,∴EH=EK,而EH⊥BF于H,EK⊥AC于K,∴AE平分∠EAC.
25、略
26、过M作MH⊥AD于H,∵∠C=∠MHD=90°,∴MH=MC,又M是BC的中点,∴MC=MB,∴MH=MB,而∠B=∠MHA=90°,∴AM平分∠DAB.
第7题
第6题
第4题
第5题
第18题
第24题
一、填空题(每小题3分,共30分)
1.已知:△ABC中,∠B=90°, ∠A、∠C的平分线交于点O,则∠AOC的度数为 .
2.角平分线上的点到_________________距离相等;到一个角的两边距离相等的点都在_____________.
3.∠AOB的平分线上一点M ,M到 OA的距离为1.5 cm,则M到OB的距离为_________.
4.如图,∠AOB=60°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=_________.
5.如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且DE=3 cm,BD=5 cm,则BC=_____cm.
6.如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、CB于点E、F,FG⊥AB,垂足为G,则CF______FG,CE________CF.
7.如图,已知AB、CD相交于点E,∠AEC及∠AED的平分线所在的直线为PQ与MN,则直线MN与PQ的关系是_________.
8.三角形的三条角平分线相交于一点,并且这一点到____________________相等.
9.点O是△ABC内一点,且点O到三边的距离相等,∠A=60°,则∠BOC的度数为_____________.
10.在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32cm,且BD∶CD=9∶7,则D到AB的距离为__________cm.
二、选择题(每小题3分,共30分)
11.三角形中到三边距离相等的点是( )
A、三条边的垂直平分线的交点 B、三条高的交点
C、三条中线的交点 D、三条角平分线的交点
12.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
A、PD=PE B、OD=OE C、∠DPO=∠EPO D、PD=OD
13.如图,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A、4处 B、3处 C、2处 D、1处
14.如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6㎝,则△DEB的周长为( )
A、4㎝ B、6㎝ C、10㎝ D、不能确定
第12题 第13题 第14题
15.如图,MP⊥NP,MQ为△MNP的角平分线,MT=MP,连接TQ,则下列结论中不正确的是( )
A、TQ=PQ B、∠MQT=∠MQP C、∠QTN=90° D、∠NQT=∠MQT
第15题 第16题 第17题
16.如图在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3 cm,那么AE+DE等于( )
A.2 cm B.3 cm C.4 cm D.5 cm
17.如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
A.① B.② C.①和② D.①②③
18.如图,AB=AD,CB=CD,AC、BD相交于点O,则下列结论正确的是( )
A.OA=OC B.点O到AB、CD的距离相等
C.∠BDA=∠BDC D.点O到CB、CD的距离相等
19.△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( )
A.2cm,2cm,2cm; B. 3cm,3cm,3cm; C. 4cm,4cm,4cm; D. 2cm,3cm,5cm
20.两个三角形有两个角对应相等,正确说法是( )
A.两个三角形全等 B.如果还有一角相等,两三角形就全等
C.两个三角形一定不全等 D.如果一对等角的角平分线相等,两三角形全等
三、解答与证明(共40分)
21.(6分)如图,已知OE、OD分别平分∠AOB和∠BOC,若∠AOB=90°,∠EOD=70°,求∠BOC的度数.
22.(6分)如图,已知△ABC中,AB=AC,D是BC的中点,求证:D到AB、AC的距离相等.
23.(7分)如图,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BD=CD.求证:AD平分∠BAC.
24.(7分)如图,已知BE平分∠ABC,CE平分∠ACD,且交BE于E.求证:AE平分∠FAC.
25.(7分)如图,已知AB=AC,AD=AE,DB与CE相交于O. (1)若DB⊥AC于D,CE⊥AB于E,试判断OE与OD的大小关系.并证明你的结论. (2)若没有第(1)中的条件,是否有这样的结论?试说明理由.
26.(7分)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:AM平分∠DAB.
《角平分线》测试题·答案
一、填空题
1、135°; 2、角的两边,这个角的平分线上; 3、1.5cm; 4、30° 5、8; 6、=,=;
7、PQ⊥MN; 8、三条边的距离; 9、120°; 10、14.
二、选择题:D D A B D ,B D D A D
三、解答题
21、50°;
22、证明:连AD,则可证△ABD≌△ACD(SSS),∴∠BAD=∠CAD,∴点D到AB、AC的距离相等.
23、简证:可得△BDF≌△CDE(AAS),∴DF=DE,又DF⊥AB,DE⊥AC,∴AD平分∠BAC.
24、简证:分别过E作EG⊥BD于G,EH⊥BF于H,EK⊥AC于K.∵BE平分∠ABC,CE平分∠ACD,∴EG=EH,EG=EK,∴EH=EK,而EH⊥BF于H,EK⊥AC于K,∴AE平分∠EAC.
25、略
26、过M作MH⊥AD于H,∵∠C=∠MHD=90°,∴MH=MC,又M是BC的中点,∴MC=MB,∴MH=MB,而∠B=∠MHA=90°,∴AM平分∠DAB.
第7题
第6题
第4题
第5题
第18题
第24题
